2018年(平成30年)度に大阪府で行われた公立高校入試B問題の数学問３の解説です。
問３は平面図形総合問題で対策線の長さから面積計算まであります。
証明がありますが、書き方を自分流で良いので型を作っておくと図の中で証明は終わります。
問題の４行目に根号を含む答えになるときの注意書きがありますが、レポートでやっているように普段通りで良いです。
長方形の対角線の長さ
(1)
会員にとっては当たり前のことで何度も言うのはくどくなりますが、
図形問題でのポイントは条件をすべて図に書き込むことです。
高校受験の場合は図が与えられるのが普通なので利用すれば良いですよ。
ただし、
図がない場合は自分で条件通り図示することで大きさな差が出てくることも忘れないでくださいね。
大学受験では図がないのが普通ですが、
書かずにいて、「三角比、平面幾何が苦手」って、
解く気がないんです。笑
学校の先生も定理や内容は伝えるけど、
『図を書くのは当たり前』っていいませんよ。
問題作成している人は図を書くのが面倒なのではありません。
問題作成段階では必ず図が存在しています。
図を書いて考える、という過程も問題にしているのです。
『覚え太郎』会員は図を書くなどの作成者の意図を意識せずにやっているだけです。
意識しておいてください。笑
前置きが長くなりましたので問題に入ります。
前置きが長いときは問題が簡単なのです。ｗ
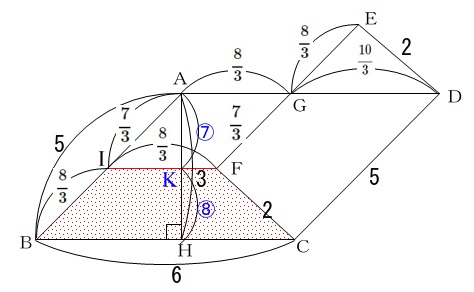
問題の3行目までの条件を図示したのが、
問題に与えてくれている\(\,図Ⅰ\,\)ですが長さが書き込まれていません。
条件をまとめておきます。
四角形\(\,\mathrm{ABCD}\,\)は平行四辺形
\(\,\mathrm{AB=5}\,\)
\(\,\mathrm{AD=6}\,\)
四角形\(\,\mathrm{EFCD}\,\)は長方形
\(\,\mathrm{ED=2}\,\)
\(\,\mathrm{BC}\,\) ⊥ \(\,\mathrm{AH}\,\)
これを図示します。
単位は答えにつければ良いので図示のときは数値だけで進めます。
わかるのはこれだけではありませんが、見にくくなるので最低限にしてあります。
①長方形の対角線の長さです。
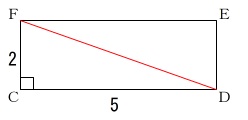三平方の定理ですね。
\(\begin{eqnarray}
\mathrm{DF^2}&=&\mathrm{DC^2+GC^2}\\
&=&5^2+2^2\\
&=&25+4\\
&=&29\\
\mathrm{DF}&=&\pm \sqrt{29}
\end{eqnarray}\)
長さなので \(\,\mathrm{DF}＞0\,\) だから
\(\,\mathrm{DF}=\underline{\sqrt{29}}\,\)
相似の証明は図の中で完成しておく
「図の中で完成してないのに証明が書けるか！」
こんなことを生徒にいっている先生は少ないかもしれませんが、
（言葉遣いの問題ではありませんよ。ｗ）
私のような凡人は、証明を書き出すまでに図の中で示せていないと証明は書けません。
では証明してみましょう。
証明はいろいろな方面から見なくてはいけないので結構やっかいです。
しかし、相似の証明にはポイントがあります。
相似条件を思い出してください。
『覚え太郎』にあるので書き出しませんが、
角度の等しいところがあるかどうかを探すのがはやいです。
\(\,\color{red}{3組の辺の比}\,\)がそれぞれ等しい、という条件はなかなか問題になりません。
全くないわけではありませんが、長さを与えまくっていては証明だけが問題になるので、
後の長さを求める、面積を求めるという誘導にしにくいからです。
※
逆に、「最後に相似の証明」となる場合は、
長さを求めるのに結構手こずる問題が先に居座ります。ｗ
多いのは「2角相当」、
\(\,\color{red}{2組の角}\,\)がそれぞれ等しい。
だから相似の証明をする場合は、
等しい角度を探しだす
ということがポイントになります。
\(\,△\mathrm{ABH}\,\) と \(\,\mathrm{△DGE}\,\) について見ていきます。
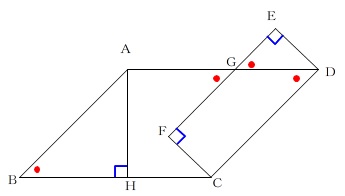
①の前に上げた問題にある条件から角度に関するものを抜き出すと、
平行四辺形だから対角は等しい。
長方形だから対辺は平行で同位角、錯角は等しい。
対頂角は等しい。
長方形の4つの角は90°
AH ⊥ BC なので\(\,\mathrm{∠AHB}\,\)=90°
（順序は気にしなくて良いです。）
などが言えるので図の角度の等しいところが2つ見つかります。
2角が等しいので相似であることが証明できています。
後はこれを数学の記号を使いながら文章にするだけです。
まとめるのが難しいと思うときは、
「角度が等しい」と見つけた順番で書いていけば良いですよ。
多少の遠回りはかまいません。
（証明）
\(\,△\mathrm{ABH}\,\) と \(\,△\mathrm{DGE}\,\) において
四角形\(\,\mathrm{ABCD}\,\)は平行四辺形で、
平行四辺形の対角は等しいから
\(\,\mathrm{∠\color{red}{ABH}=∠\color{magenta}{ADC}}\,\) ･･･①
四角形\(\,\mathrm{EFCD}\,\)は長方形で対辺は平行なので錯角が等しいから
\(\,\mathrm{∠\color{magenta}{ADC}=∠\color{blue}{DGE}}\,\) ･･･②
①②から
\(\,\mathrm{∠\color{red}{ABH}=∠\color{blue}{DGE}}\,\) ･･･③
また、\(\,\mathrm{AH}\,\) ⊥ \(\,\mathrm{BC}\,\) なので
\(\,\mathrm{∠\color{green}{AHB}}=\color{magenta}{90°}\,\) ･･･④
長方形\(\,\mathrm{EFCD}\,\)の4つの内角は直角なので
\(\,\mathrm{∠\color{orange}{DEG}}＝\color{magenta}{90°}\,\) ･･･⑤
④⑤より
\(\,\mathrm{∠\color{green}{AHB}=∠\color{orange}{DEG}}\,\) ･･･⑥
③⑥より
2組の角がそれぞれ等しいので
\(\,\mathrm{△ABH}\,\) ∽ \(\,\mathrm{△DGE}\,\) （終わり）
錯角と90°の順序は逆でもいいですし、
錯角に飛びましたが、同位角から対頂角に移っても同じことです。
きれいにまとめようとする必要はありません。
高校生になれば相似の証明をすることはなくなります。
相似は見つけて当たり前状態で問題が作られますので、
図の中で見つけるしかないのです。
簡単に言えば、
『 図に示した通り
\(\,\mathrm{△ABH}\,\) ∽ \(\,\mathrm{△DGE}\,\)
なので』
と解答が続きます。
相似の証明後の線分の長さを求める問題
相似の証明の後に出てくる長さを求める問題では、
証明した相似な三角形の相似比を利用
する問題がほとんどです。
たまに、関係ない小問集合のような問題もありますが、
あれ？、と拍子抜けします。笑
(2)(1)の\(\,図Ⅰ\,\)に条件が加わります。
\(\,\mathrm{AH}=3\,\)
\(\,\mathrm{IF}\,\) ∥ \(\,\mathrm{BC}\,\)
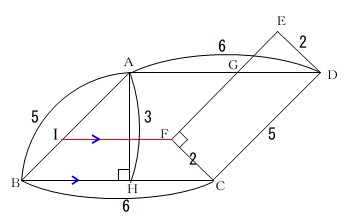
で？何を求める？
①線分\(\,\mathrm{GD}\,\)の長さです。
あれこれ考えても良いですが、
なぜ相似の証明をしたのだろうか？
と思えるようになってくると良いですね。
\(\,\mathrm{△ABH}\,\) ∽ \(\,\mathrm{△DGE}\,\)
ここにちゃんと線分\(\,\mathrm{GD}\,\)が含まれているので楽勝です。
ニコちゃんマークですね。(^_^)v
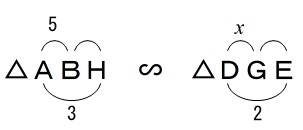
三平方の定理を使えば\(\,\mathrm{BH}\,\)も求まるので全部の辺の長さが出ますが、後でやりましょう。
比例式を立てます。
\(\begin{eqnarray}
\mathrm{AB:DG}&=&\mathrm{AH:DE}\\
5:x&=&3:2\\
3x&=&10\\
\displaystyle x&=&\underline{\frac{10}{3}}
\end{eqnarray}\)
むっちゃストレートな問題やな。笑
面積は直接計算か圧縮か
②はややこしそうです。
四角形\(\,\mathrm{IBCF}\,\)の面積です。
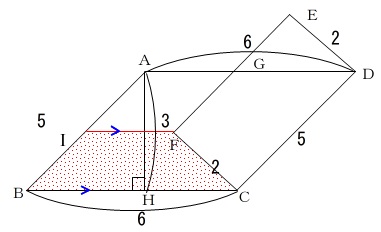台形ですね。
相似、三平方の定理などを使うとすべての長さはわかりますが、
求めた長さから簡単に出てくる長さだけを示しておきましょう。
ここからが地味ですが必要な計算です。
大阪\(\,\mathrm{B}\,\)問題ではこれくらいはあると覚悟しておけば大丈夫です。
※
中学生らしい突っ走るタイプの求め方です。
平行四辺形から圧縮する方法は後で示しておきます。
①から \(\,\displaystyle \mathrm{\color{red}{GD}}=\frac{10}{3}\,\)
\(\begin{eqnarray}
\mathrm{\color{red}{AG}}&=&\mathrm{AD-GD}\\
\displaystyle &=&6-\frac{10}{3}\\
&=&\frac{18-10}{3}\\
&=&\frac{8}{3}
\end{eqnarray}\)
\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)∥\(\,\mathrm{GF}\,\)なので
\(\,\mathrm{AIFG}\,\)は平行四辺形になるから
\(\,\displaystyle \mathrm{\color{red}{IF}}=\mathrm{AG}=\frac{8}{3}\,\)
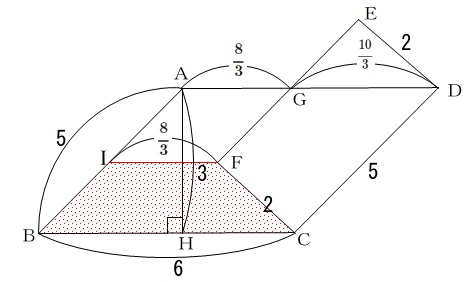台形の上底と下底はわかりました。
高さが必要ですが直接出せる線分はありません。
\(\,\mathrm{AH}\,\)と\(\,\mathrm{IF}\,\)の交点を\(\,\mathrm{K}\,\)としましょう。（記号は何でも良いですよ。）
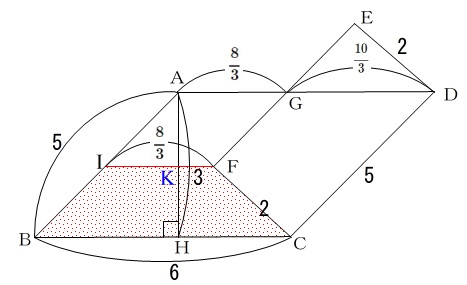台形の高さとなる\(\,\mathrm{KH}\,\)の長さも直接は出ません。
順を追っていくと
\(\,\mathrm{AH}\,\)がわかっているので\(\,\mathrm{AK:KH}\,\)がわかれば良い、
\(\,\mathrm{△AIK}\,\) ∽ \(\,\mathrm{△ABH}\,\) の相似比がわかれば良い、
\(\,\mathrm{AI}\,\)がわかれば良い、
\(\,\mathrm{GF}\,\)がわかれば良い、
となるのですが、
出せるところを1つでも見つけて出してみる
と視界が開けることがあります。
直角三角形を見つけたら三平方の定理
が使えないか、試すのは普通の流れとして良いでしょう？
\(\,\mathrm{△ABH}\,\)は直角三角形なので
\(\begin{eqnarray}
\mathrm{AH^2+BH^2}&=&\mathrm{AB^2}\\
3^2+\mathrm{BH^2}&=&5^2\\
\mathrm{BH^2}&=&25-9\\
&=&16\\
\mathrm{BH}&=&\pm 4
\end{eqnarray}\)
\(\,\mathrm{BH}＞0\,\)（長さ）だから
\(\,\mathrm{BH}=4\,\)
これは\(\,3：4：5\,\)の辺の比の三角形は直角三角形、というのを知っていれば三平方の定理を使わなくても出して良いですよ。
\(\,\mathrm{△DGE}\,\)も直角三角形なので三平方の定理を使うか、
証明した\(\,\mathrm{△ABH}\,\)∽\(\,\mathrm{△DGE}\,\)の相似比を使うか、
どちらでも良いので\(\,\mathrm{GE}\,\)を求めることができます。
三平方の定理にも飽きてくるので相似比で比例式を立てましょう。
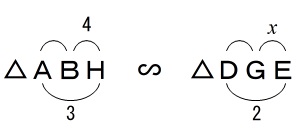ニコちゃんマークです。
\(\begin{eqnarray}
\mathrm{AH:DE}&=&\mathrm{BH:GE}\\
3:2&=&4:\mathrm{GE}\\
3\times \mathrm{GE}&=&2\times 4\\
\displaystyle \mathrm{GE}&=&\frac{8}{3}
\end{eqnarray}\)
これが出てくれば
\(\begin{eqnarray}
\mathrm{GF}&=&\mathrm{EF-GE}\\
\displaystyle &=&5-\frac{8}{3}\\
&=&\frac{15-8}{3}\\
&=&\frac{7}{3}
\end{eqnarray}\)
\(\,\mathrm{AIFG}\,\)は平行四辺形なので
\(\,\displaystyle \mathrm{AI}=\frac{7}{3}\,\)
\(\begin{eqnarray}
\mathrm{IB}&=&\mathrm{AB-AI}\\
&=&5-\frac{7}{3}\\
&=&\frac{8}{3}
\end{eqnarray}\)
相似比が出ました。
\(\,\mathrm{△AIK}\,\)と\(\,\mathrm{△ABH}\,\)の相似比は
\(\displaystyle \frac{7}{3}:5=7:15\)
これは\(\,\mathrm{AI:IB}=7:8\,\)ということなので
\(\,\mathrm{AK:KH}=7:8\,\)
\(\,\mathrm{AH:KH}=15:8\,\)となるので
\(\begin{eqnarray}
\displaystyle \mathrm{KH}&=&\frac{8}{15}\times 3\\
&=&\frac{8}{5}
\end{eqnarray}\)
これが台形の高さです。
よって四角形\(\,\mathrm{IBCF}\,\)（台形）の面積は
\(\displaystyle \hspace{10pt} \frac{\frac{8}{3}+6}{\color{red}{2}}\times \frac{8}{5}\\
\displaystyle =\left(\frac{8}{3}+6\right)\color{red}{\div 2}\times \frac{8}{5}\\
\displaystyle =\frac{8+18}{3}\times \frac{1}{2}\times \frac{8}{5}\\
\displaystyle =\frac{26}{3}\times \frac{1}{2}\times \frac{8}{5}\\
\displaystyle =\frac{13\times 8}{3\times 5}\\
\displaystyle =\underline{\frac{104}{15}}\)
説明するとものすごく長いですが、実際に計算すれば大して時間はかかりません。
やるかやらないかだけなので、
これくらいの計算が待っているということを知っていれば\(\,\mathrm{B}\,\)問題はクリアーできます。
これは公立高校入試の標準レベルです。
都道府県や大阪府のように\(\,\mathrm{A,B,C}\,\)と分かれている問題が用意されている場合は、
これよりも簡単な問題がそろう場合もありますが、
全国的に計算量はここを基準にしておくと良いでしょう。
試験を受ける前に、どれだけ覚悟しておくかで大きく変わるという話でした。
これだけを言うためにえらい時間かかった。笑
ついでにちょっとした応用編の解き方も示しておきます。
平行四辺形を圧縮します。
\(\,\mathrm{△DGE}\,\)が\(\,3：4：5\,\)の直角三角形だとわかったら\(\,\mathrm{GE}\,\)の長さが出ます。
\(\,\mathrm{EF}=5\,\)なので
\(\,\displaystyle \mathrm{GF}=5-\mathrm{GE}=\frac{7}{3}\,\)
\(\,\mathrm{EF}\,\)の延長と\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{M}\,\)とすると
\(\displaystyle \mathrm{FM}=5-\mathrm{GF}=\frac{8}{3}\,\)
平行四辺形の対辺どうしなので
\(\hspace{10pt}\mathrm{AI:IB}\\
=\mathrm{GF:FM}\\
=\mathrm{DL:LC}\\
=\color{blue}{7:8}\,\)
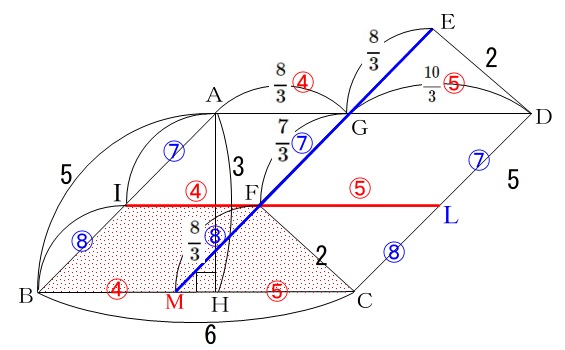同じように\(\,\mathrm{IF}\,\)の延長と\(\,\mathrm{DC}\,\)の交点を\(\,\mathrm{L}\,\)とすると、
\(\hspace{10pt}\mathrm{AG:GD}\\
=\mathrm{IF:FL}\\
=\mathrm{BM:MC}\\
=\color{red}{4:5}\,\)
ここからは足すか引くかで方法が分かれます。
比で出しても良いのですが平行四辺形\(\,\mathrm{ABCD}\,\)の面積は
\(6\times 3=18\)
と具体的に求まるのでこれを使いましょう。
\(\begin{eqnarray}
台形\mathrm{IBCF}&=&平行四辺形\mathrm{IBMF}+\mathrm{△FMC}\\
&=&\color{blue}{\frac{8}{15}}\times \color{red}{\frac{4}{9}}\times 18+\color{blue}{\frac{8}{15}}\times \color{red}{\frac{5}{9}}\times 18\times \frac{1}{2}\\
&=&\frac{8\times 4\times 18}{15\times 9}+\frac{8\times 5\times 18}{15\times 9\times 2}\\
&=&\frac{8\times 4\times 2}{15}+\frac{8\times 5}{15}\\
&=&\frac{64+40}{15}\\
&=&\underline{\frac{104}{15}}
\end{eqnarray}\)
または
\(\begin{eqnarray}
台形\mathrm{IBCF}&=&平行四辺形\mathrm{IBCL}-\mathrm{△FLC}\\
&=&\color{blue}{\frac{8}{15}}\times 18-\color{blue}{\frac{8}{15}}\times \color{red}{\frac{5}{9}}\times 18\times \frac{1}{2}\\
&=&\frac{8\times 18}{15}-\frac{8\times 5\times 18}{15\times 9\times 2}\\
&=&\frac{8\times 18}{15}-\frac{8\times 5}{15}\\
&=&\frac{144-40}{15}\\
&=&\underline{\frac{104}{15}}
\end{eqnarray}\)
忘れてくれて良いです。
実際の試験会場では具体的に台形の面積を求めるように突っ走った方が中学生にははやいです。
どちらにしてもわかる線分の長さを出すということに変わりはありませんよ。
⇒ 2018年度大阪府公立高校入試Ｂ問題の数学問4空間図形の解説
あと一つ空間図形が残っていますが、空間図形でのポイントは一つです。
ここまでどれくらいの計算量と時間がかかっているか見ておくと良いです。
おおよそですが、大阪府の\(\,\mathrm{B}\,\)問題は毎年同じくらいの分量と考えていて良いですよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
