2023年(令和5年)度埼玉県公立高校入試【学校選択問題】数学の解説

2023年(令和5年)度埼玉県公立高校入試【学校選択問題】数学の問題と解説です。
昨年度とは違い問題構成が良いので、
多少は応用が必要になりますが良い復習と程よい応用の練習になると思います。
一般問題と同じものもあるのでその部分の解説は簡単に済ませます。

2023年(令和5年)度埼玉県公立高校入試【学校選択問題】数学の問題PDF

改めていう必要もないでしょうけど、
復習のために利用する他県の人にお伝えしてきます。
埼玉県では基礎重視の【一般問題】と基礎から標準、応用まで問われる【学校選択問題」があります。

令和５年度の【学校選択問題】数学の問題です。

⇒　2023年(令和5年)度埼玉県公立高校入試【学校選択問題】数学の問題PDF

ページ数は一般問題と同じですが質問内容は多少違います。
問題数も一般は４問ですが学校選択は５問になります。

2023年(令和5年)度埼玉県公立高校入試【学校選択問題】数学の解説

総問題数は一般と学校選択でそれ程差はありません。
ただし、学校選択問題は要領良くこなさないと計算にも時間がかかるので、
計算方法などの基本もしっかり身に付けておく必要がありますね。

一般問題と重複している問題は解説を省きますので一般問題の解説を見ておいて下さい。

学校選択問題を選択する時点である程度の基礎はできているものとして解説を進めます。

第１問

\(\,\large{1}\,\)
(1)
　\(\hspace{10pt}\displaystyle 10xy^2\times \left(-\frac{2}{3}\,xy \right)^2\div (-5y^2)\\
\displaystyle =-10xy^2\times \frac{4x^2y^2}{9}\times \frac{1}{5y^2}\\
\displaystyle =-\frac{10xy^2\times 4x^2y^2}{9\times 5y^2}\\
\displaystyle =\underline{\underline{　-\frac{8\,x^3\,y^2}{9}　}}\)

符号に気をつけて、後はいつも通りの計算です。
２行目は省略しても良いでしょう。

(2)
条件式からか、与式（求値式）からか、
会員は迷う程でもないでしょう。
　\(\begin{eqnarray}
(\,与式\,)&=&x^3y-xy^3\\
&=&xy(x^2-y^2)\\
&=&xy(x+y)(x-y)
\end{eqnarray}\)
※
交代式なので\(\,(x-y)\,\)まで必要ですね。
条件式から
　\(\hspace{10pt}x+y=(3+\sqrt{7})+(3-\sqrt{7})=\color{red}{6}\)
　\(\hspace{10pt}x-y=(3+\sqrt{7})-(3-\sqrt{7})=\color{blue}{2\sqrt{7}}\)
　\(\hspace{10pt}xy=(3+\sqrt{7})(3-\sqrt{7})=\color{magenta}{2}\)
よって、
　\(\begin{eqnarray}
x^3y-xy^3&=&xy(x+y)(x-y)\\
&=&\color{red}{6}\times \color{blue}{2\sqrt{7}}\times \color{magenta}{2}\\
&=&\underline{　24\sqrt{7}　}
\end{eqnarray}\)

くっそていねいいにやっていますがもっとさらっと終わらせて良いですよ。
間違っても直接代入、だけはやめておきましょう。
（３乗展開だけは避けて下さい。）

(3)
２次方程式ですがあからさまにまとまりが見えるので置換します。
　\(\hspace{4pt}(\color{magenta}{5x-2})^2-2(\color{magenta}{5x-2})-3=0\)
\(\,5x-2=t\,\)とおくと
　\(\begin{eqnarray}
t^2-2t-3&=&0\\
(t+1)(t-3)&=&0\\
t&=&\color{red}{-1}\,,\,\color{blue}{3}
\end{eqnarray}\)
元に戻して
　\(\begin{eqnarray}
5x-2&=&\color{red}{-1}\\
x&=&\frac{1}{5}
\end{eqnarray}\)
または
　\(\begin{eqnarray}
5x-2&=&\color{blue}{3}\\
x&=&1
\end{eqnarray}\)
答え　\(\displaystyle \underline{\underline{　x=\frac{1}{5}\,,\,1　}}\)

展開しても良いですが、お勧めしません。

(4)
一般問題の\(\,\large{1}\,\)(9)と同じです。
答え　\(\,\underline{　ア　と　ウ　}\,\)
(5)
一般問題の\(\,\large{1}\,\)(13)と同じです。
答え　\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{5}{8}　}}\)
\(\,50\,\)円玉の区別は忘れずに樹形図です。
(6)
一般問題の\(\,\large{1}\,\)(14)と同じです。答え　\(\hspace{4pt}\underline{　33\,\pi　}\,(\,\mathrm{cm^2}\,)\)
(7)
合同な台形と正三角形でできている錐台です。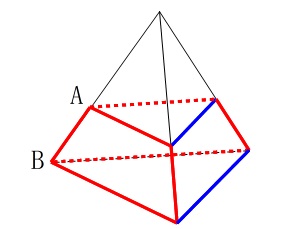答え
　頂点　\(\,\underline{　6\,個　}\)、　辺　\(\,\underline{　9\,本　}\,\)、　ねじれの位置　\(\,\underline{　2\,本　}\,\)
延長して交わるものはねじれの位置ではありません。

(8)
十のくらいは固定なので使う文字は２つです。
百のくらい\(\,a\,\)、十の位\(\,7\,\)、一の位\(\,b\,\)とします。
　\(\hspace{4pt}\mathrm{X}=100a+70+b\)
　\(\hspace{4pt}\mathrm{Y}=100b+70+a\)

各位の数の和が\(\,15\,\)なので
　\(\begin{eqnarray}a+7+b&=&15\\
a+b&=&8　･･･①\end{eqnarray}\)
\(\,\mathrm{X}\,\)と\(\,\mathrm{Y}\,\)の差が\(\,396\,\)なので
　\(\begin{eqnarray}
\mathrm{X-Y}&=&396\\
99a-99b&=&396\\
a-b&=&4　･･･②
\end{eqnarray}\)
\(\,①\,,\,②\,\)から
　\(\hspace{4pt}a=6\,,\,b=2\)
よって求める\(\,\mathrm{X}\,\)は
　\(\hspace{10pt}\mathrm{X}=\underline{　672　}\)

簡単な連立方程式なので計算は省略しました。
(9)
２次関数の変域です。
　\(\hspace{4pt}y=2x^2\,,\,(\,a\,≦\,x\,≦\,a+4\,)\)
\(\,y\,\)の範囲は\(\,0\,≦\,y\,≦\,18\,\)なので、
原点（\(\,y\,\)軸）は含む範囲で場合は２つ考えられます。
一つは\(\,x=a\,\)が\(\,x=a+4\,\)より\(\,y\,\)軸から離れている場合で、
もう一つは\(\,x=a+4\,\)が\(\,x=a\,\)より\(\,y\,\)軸から離れている場合。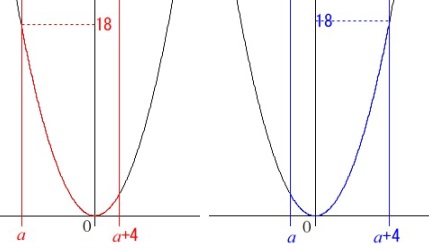つまり、
最大値\(\,18\,\)が\(\,x=\color{red}{a}\,\)のときか、\(\,x=\color{blue}{a+4}\,\)のときかです。
どちらにしても\(\,a\,≦\,0\,≦\,a+4\,\)でなくてはなりません。
（\(\,x\,\)の範囲は\(\,0\,\)を含む。）

\(\,x=\color{red}{a}\,\)のとき最大値\(\,18\,\)となる場合、
　\(\begin{eqnarray}
18&=&2\,(\,\color{red}{a}\,)^2\\
a&=&\pm 3
\end{eqnarray}\)
から\(\,a=-3\,\)。（\(\,a=+3\,\)は不適。）

\(\,x=\color{blue}{a+4}\,\)のとき最大値\(\,18\,\)となる場合、
　\(\begin{eqnarray}
18&=&2\,(\,\color{blue}{a+4}\,)^2\\
a+4&=&\pm 3\\
a&=&-1\,,\,-7
\end{eqnarray}\)
から\(\,a=-1\,\)。（\(\,a=-7\,\)は不適。）

答え　\(\,a=\underline{　-3\,,\,-1　}\,\)

それぞれ不適とした場合は最小値が\(\,0\,\)にならないことを確認して下さい。
(10)
一般問題の\(\,\large{1}\,\)(16)と同じです。
ここではイの箱ひげ図だけが与えられています。「第３四分位数は、
ヒストグラムから\(\,40\,\)分以上\(\,50\,\)分未満の階級にあるが、
箱ひげ図では\(\,50\,\)分以上\(\,60\,\)分未満の階級にあるから。」

第２問

\(\,\large{2}\,\)
作図と合同の証明です。
(1)
２時間で\(\,30°\,\)移動します。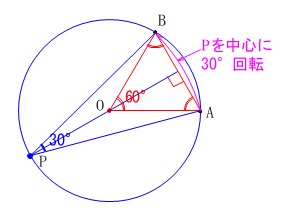\(\,30°\,\)の作図ですがイメージとしては、
正三角形から中心角\(\,60°\,\)を描いて、
円周角の定理から\(\,30°\,\)をつくります。
ただし円周角だけだと周上のどこか定まらないので、
線分\(\,\mathrm{AB}\,\)の垂直二等分線と円との交点が\(\,\mathrm{P}\,\)となります。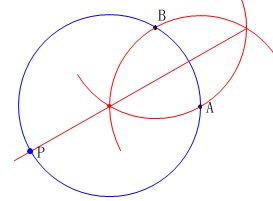中心をイメージできれば作図はシンプルです。

こうやってみると、一般問題は定規なしで作図できることも分かりますね。

(2)
合同の証明です。
条件は平行四辺形\(\,\mathrm{ABCD}\,\)に加えて、
　\(\hspace{10pt}\mathrm{AE=BF=CG=DH}\)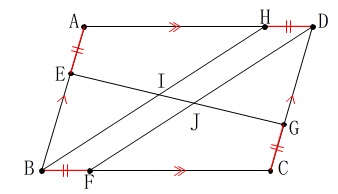このとき
　\(\,\mathrm{△BEI}\,\)≡\(\,\mathrm{△DGJ}\,\)
を証明します。

問題の条件（仮定）から
　\(\,\mathrm{HD}\,\)∥\(\,\mathrm{BF}\,\)
　\(\hspace{4pt}\mathrm{HD=BF}\)
なので四角形\(\,\mathrm{BFDH}\,\)は平行四辺形です。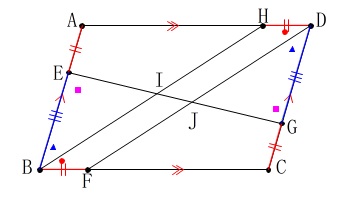図の中で証明は終わっているので後はまとめるだけです。
（図の条件はあとで順に追っておきます。）

ここでまとめ的な話になりますが、
この年度の問題は昨年とはかなり違っていて、
（個人的にですが）かなり良い問題だと思います。

計算がめったやたらに困難な訳でもなく、
重っ苦しい匂いもしない。

単に公式を覚えていればどうこうなるものでもないし、
（『超え太郎』マスターには単純に思えるだろうけどそこは仕方ない。）
数学の基本作業を重視しているところは応用練習にも非常に参考になる。
特に\(\,\large{5}\,\)は難しく考えないところに答えがあるのでダマシ的な問題でもあり面白い。
説明を自分の言葉で表現させるところは受験生には少し厳しいかもしれませんが、
基本的なルールをしっかり抑えておけばクリアーできるでしょう。

ということで、元に戻り解説しておきます。
証明はルールに従って自分の言葉でまとめて下さい。

平行四辺形の対角が等しいことから
　\(\hspace{10pt}\mathrm{∠ABC}=\mathrm{CDA}\)
　\(\hspace{10pt}\mathrm{∠HBF}=\mathrm{∠FDH}\)
等しい角から等しい角を引くので
　\(\hspace{10pt}\mathrm{\color{blue}{∠EBI}}=\mathrm{\color{blue}{∠GDJ}}　･･･①\)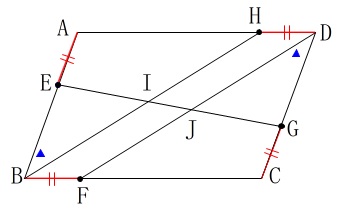平行四辺形の対辺は平行なので錯角が等しく
　\(\hspace{10pt}\mathrm{\color{magenta}{∠BEI}}=\mathrm{\color{magenta}{∠DGJ}}　･･･②\)また平行四辺形の対辺は等しく、
　\(\hspace{10pt}\mathrm{AB=DC}\)
仮定から
　\(\hspace{10pt}\mathrm{AE=CG}\)
等しい辺から等しい辺を引くので
　\(\hspace{10pt}\mathrm{\color{blue}{BE}}=\mathrm{\color{blue}{DG}}　･･･③\)\(\,①②③\,\)から、
「１組の辺とその両端の角がそれぞれ等しい。」
よって、\(\,\mathrm{△BEI}\,\)≡\(\,\mathrm{△DGJ}\,\)

平行線が多いので他の方針でも条件はそろうでしょう。

⇒　中学２年平行と合同と証明の書き方ポイントまとめ

平行四辺形における角度はどうとっても良いですが、
合同条件をそろえる場合の角度は記号と順番には気をつけておきましょう。

第３問

\(\,\large{3}\,\)
一般問題の\(\,\large{3}\,\)とほぼ同じなので説明は簡単に済ませます。
(1)
一般問題\(\,\large{3}\,\)(1)と同じです。
　\(\hspace{10pt}ア　\underline{　6　}　イ　\underline{　25　}\)
(2)
商は実際に割り算してもしれていますが問題にあります。
　\(\hspace{10pt}\displaystyle \frac{1}{7}=0.\color{red}{142857}\color{blue}{142857}14\cdots \)

小数第１位から６つの数字で循環します。
　\(\hspace{10pt}30=6\times 5\)
小数第\(\,30\,\)位はちょうど循環の最後で終わるので答えは分かりやすいです。

答え　\(\,\underline{　7　}\,\)　

また各位の数の和は循環する\(\,6\,\)つの数の和\(\,5\,\)回分なので
　\(\hspace{10pt}(\,1+4+2+8+5+7)\times 5\\
=27\times 5=\underline{　135　}\)

次いきます。

第４問

\(\,\large{4}\,\)
関数の基本確認と回転体の体積です。
(1)
比例定数と傾き、\(\,y\,\)切片に着目します。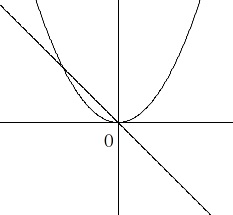下に凸（上に開いている）なので\(\,y=ax^2\,\)の比例定数\(\,a\,\)は
　\(\hspace{10pt}a\,＞\,0\)
直線は原点を通り\(\,x\,\)が増加すると\(\,y\,\)は減少しているので、
\(\,y=bx+c\,\)において
　\(\hspace{10pt}b\,＜\,0\,,\,c=0\)
よって、
　\(\hspace{10pt}\underline{　b\,＜\,c\,＜\,a　}\)

\(\,c=0\,\)を基準にみると明らかです。
図\(\,\mathrm{Ⅰ}\,\)に限っていえることなので間違えないように。

(2)
文字がいっぱいあるように見えるのでややこしいですが、
四角形\(\,\mathrm{PQRS}\,\)が台形なので、
\(\,\mathrm{P}\,\)と\(\,\mathrm{S}\,\)、\(\,\mathrm{Q}\,\)と\(\,\mathrm{R}\,\)は\(\,x\,\)座標が同じです。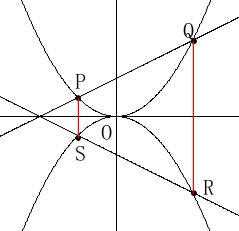

つまり、\(\,x\,\)軸対称な図形があると思えば少しは分かり易いでしょう。
二つの直線の交点は\(\,x\,\)軸上にあります。
①
　\(\hspace{10pt}y=ax^2\,,\,y=bx+c\)
において\(\,a\,\)と\(\,b\,\)を変えないまま\(\,c\,\)を大きくすると、
直線の\(\,y\,\)切片の絶対値が大きくなるので、
交点\(\,\mathrm{P\,,\,Q}\,\)の\(\,x\,,\,y\,\)座標ともに絶対値は大きくなります。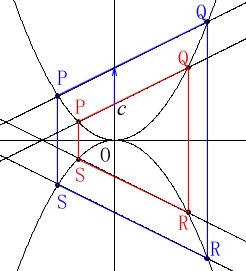対称な図形なので上底、下底、高さすべて大きくなるので、
台形の面積は大きくなります。

答え　\(\,\underline{　ア　}\,\)

説明では\(\,\mathrm{S\,,\,R}\,\)を使って長さを表せば書きやすいでしょう。

②
座標が登場します。
　「点\(\,\mathrm{P\,,\,Q}\,\)の\(\,x\,\)座標がそれぞれ\(\,-1\,,\,2\,\)」

条件は「直線\(\,\mathrm{QS}\,\)の傾きが\(\,1\,\)」です。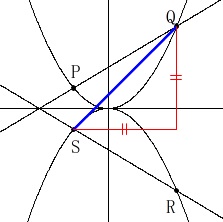条件から各定数が定まり各点が具体的に求まるはずですが、
各点はどちらの関数上の点でもあるのでどちらから進めるかで分かれるでしょう。

直線上の点という条件からだと文字二つを扱うことになるので、
関数\(\,y=ax^2\,\)上の点ということから進めます。
与えられた\(\,x\,\)座標からそれぞれの点を\(\,a\,\)を用いて表すと
　\(\hspace{10pt}\mathrm{P}\,(\,-1\,,\,a\,)\)
　\(\hspace{10pt}\mathrm{Q}\,\color{red}{(\,2\,,\,4a\,)}\)
　\(\hspace{10pt}\mathrm{S}\,\color{blue}{(\,-1\,,\,-a\,)}\)
　\(\hspace{10pt}\mathrm{R}\,(\,2\,,\,-4a\,)\)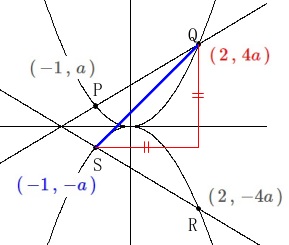「直線\(\,\mathrm{QS}\,\)の傾きが\(\,1\,\)」なので
　\(\begin{eqnarray}
\frac{4a-(-a)}{2-(-1)}&=&1\\
5a&=&3\\
a&=&\underline{\underline{　\frac{3}{5}　}}
\end{eqnarray}\)
このとき
　\(\hspace{10pt}\displaystyle \mathrm{P}\,\left(\,-1\,,\,\frac{3}{5}\,\right)\)
　\(\hspace{10pt}\displaystyle \mathrm{Q}\,\left(\,2\,,\,\frac{12}{5}\,\right)\)
直線\(\,y=bx+c\,\)はこの２点を通るので\(\,b\,,\,c\,\)を求める事ができます。
（\(\,\mathrm{S\,,\,R}\,\)と\(\,y=-bx-c\,\)でも良いですよ。）

連立方程式を解いても良いのですが、
逆にこの２点を通る直線を求めて\(\,b\,,\,c\,\)と対応させます。

２点\(\,\mathrm{P\,,\,Q}\,\)において
　\(\hspace{4pt}(\,x\,の増分\,)=\,2-(-1)\,=\,3\)
　\(\hspace{4pt}\displaystyle (\,y\,の増分\,)=\,\frac{12}{5}-(\frac{3}{5})\,=\,\frac{9}{5}\)
なので傾き\(\,b\,\)は
　\(\begin{eqnarray}
b&=&\frac{9}{5}\div 3\\
&=&\underline{\underline{　\frac{3}{5}　}}
\end{eqnarray}\)
直線の式は
　\(\hspace{10pt}\displaystyle y=\frac{3}{5}\,x+c\)
とおけてこれが点\(\,\mathrm{P}\,\)を通ることから（点\(\,\mathrm{Q}\,\)でも良いです。）
　\(\begin{eqnarray}
\frac{3}{5}&=&\frac{5}{3}\times (-1)+c\\
c&=&\underline{\underline{　\frac{6}{5}　}}
\end{eqnarray}\)

比例定数\(\,a\,\)が求まった時点で\(\,b\,,\,c\,\)は分数計算ができれば問題ないでしょう。
傾きを計算するとき
　\(\hspace{10pt}\displaystyle \frac{\frac{9}{5}}{3}=\frac{9}{5}\times \frac{1}{3}\)
の処理ができれば普段の傾きを求める計算と同じです。

さて、回転体の体積が残っています。
（円錐台の体積なので公式もありますがここでは引き算で求めておきます。）
※
会員は『超え太郎』－「座標と図形」\(\,\mathrm{No.113}\,\)を確認しておいて下さい。
（ただし、分数の場合お勧めはしません。）

関数と交点をみておきます。
　\(\hspace{10pt}\displaystyle y=\frac{3}{5}\,x^2\)
　\(\hspace{10pt}\displaystyle y=\frac{3}{5}\,x+\frac{6}{5}\)
の交点\(\,\mathrm{P\,,\,Q}\,\)の座標は
　\(\hspace{10pt}\displaystyle \mathrm{P}\,\left(\,-1\,,\,\frac{3}{5}\,\right)\)
　\(\hspace{10pt}\displaystyle \mathrm{Q}\,\left(\,2\,,\,\frac{12}{5}\,\right)\)
直線と\(\,x\,\)軸との交点は
　\(\begin{eqnarray}
0&=&\frac{3}{5}\,x+\frac{6}{5}\\
x&=&-2
\end{eqnarray}\)
から\(\,(\,-2\,,\,0\,)\,\)です。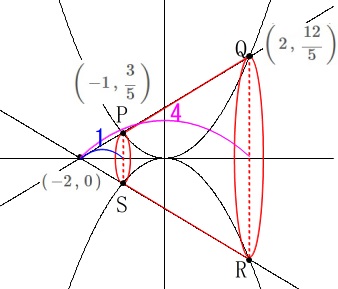求める回転体の体積\(\,V\,\)は円錐から円錐を引けば良いので、
　\(\begin{eqnarray}
V&=&\frac{1}{3}\,\pi\,\left(\frac{12}{5}\right)^2\times 4-\frac{1}{3}\,\pi\,\left(\frac{3}{5}\right)^2\times 1\\
&=&\frac{1}{3}\,\pi\,\times \frac{144}{25}\times 4-\frac{1}{3}\,\pi\,\times \frac{9}{25}\\
&=&\frac{48\times 4}{25}\,\pi-\frac{3}{25}\,\pi\\
&=&\frac{192-3}{25}\,\pi\\
&=&\underline{\underline{　\frac{189}{25}\,\pi　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

円錐から円錐を引くと分かったら、
底面の半径（\(\,y\,\)座標）と高さ（\(\,x\,\)座標の差）に気をつけて、
後は計算だけなので計算過程は好きにして下さい。
空白で部分的に計算すればそれ程ややこしくは感じないはずです。

第５問

\(\,\large{5}\,\)
直方体における動点問題です。

問題の条件は自分で読み取っておいて下さい。
一般問題と違うのは点が二つ動くところですが、
二つの点は同じ速さで動くので割ととらえやすいです。
(1)
一般問題\(\,\large{4}\,\)(1)と同じです。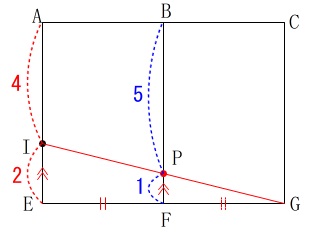答え　\(\,\underline{　5　}秒後\,\)

理由はしっかり確認しておきましょう。
(2)
点\(\,\mathrm{P\,,\,Q}\,\)は同じ速さで動くので\(\,\mathrm{BD}\,\)と\(\,\mathrm{PQ}\,\)は平行です。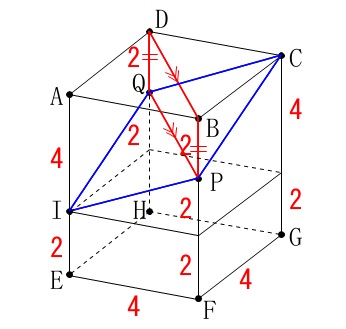直線\(\,\mathrm{PQ}\,\)を軸にまわる平面で切られるので、
頂点\(\,\mathrm{A}\,\)を含む立体の体積\(\,V\,\)は、
点\(\,\mathrm{I}\,\)を通り面\(\,\mathrm{ABCD}\,\)と平行な平面でできる直方体の半分になるから
　\(\begin{eqnarray}
V&=&\frac{1}{2}\times 4\times 4\times 4\\
&=&\underline{　32　}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)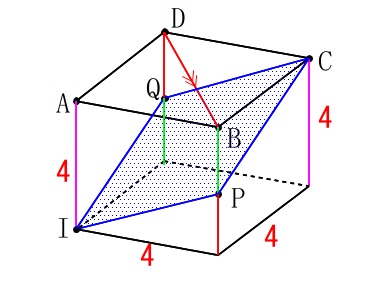図の頂点\(\,\mathrm{A}\,\)を含む立体と下にある立体が合同だということです。直線\(\,\mathrm{PQ}\,\)を含む面\(\,\mathrm{ABCD}\,\)に平行な面（緑の面）と、
頂点\(\,\mathrm{I}\,\)と頂点\(\,\mathrm{C}\,\)でつくられる三角錐が同じ大きさです。
（合同といっても通じるでしょう。）
直線\(\,\mathrm{PQ}\,\)を軸に面が回転すると、
\(\,\mathrm{I}\,\)が動く分\(\,\mathrm{C}\,\)も逆に動くので高さが等しいことは分かるでしょう。
（底面の直角二等辺三角形も合同なので三角錐が合同です。）
つまり、頂点\(\,\mathrm{A}\,\)を含む立体と、直方体の残りと同じだということです。

元の直方体からでも同じように求める事ができます。
面\(\,\mathrm{IPCQ}\,\)で切り取り、
下の部分をひっくり返してくっつけてみると分かります。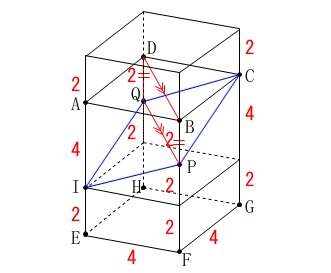高さ\(\,8\,\)の直方体ができていればその半分が、
頂点\(\,\mathrm{A}\,\)を含まない方の体積です。

かなりメンドウにはなりますが、
分割して四角錐、三角錐、三角柱の体積を加えても良いですよ。

まあ、体積は『超え太郎』の公式や考え方ですぐにでるので、
記号を加えて説明を簡単に済ませるのが良いですね。

(3)
球面と平面の接点の問題です。球の半径は\(\,\color{red}{2}\,\)で直方体に接しています。立体や平面でとらえるのは得策ではないので線に変えたいですね。

面\(\,\mathrm{IPQ}\,\)が線に見えるのは\(\,\mathrm{B\,,\,D}\,\)が重なるようにみたときです。
球の中心を\(\,\mathrm{O}\,\)、接点を\(\,\mathrm{T}\,\)としておきます。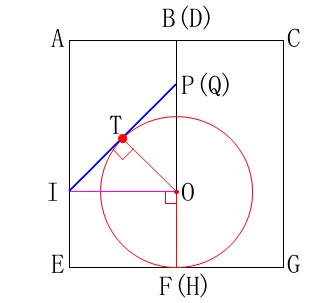直角二等辺三角形があります。
　\(\,\mathrm{△OTI\,,\,△OIP}\,\)
ここまでくれば後は長さを加えれば簡単です。
　\(\hspace{10pt}\mathrm{OT=OF}=\color{red}{2}\)
　\(\hspace{10pt}\mathrm{OI=OP}=\color{magenta}{2\sqrt{2}}\)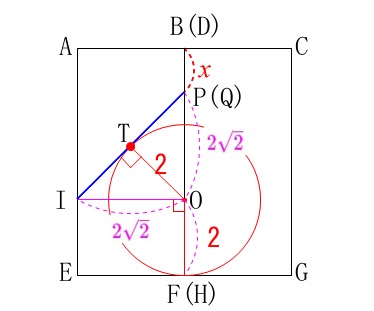求める\(\,x\,\)は線分\(\,\mathrm{BP}\,\)と同じで、
　\(\begin{eqnarray}
x&=&\mathrm{BF-PF}\\
&=&6-(\color{red}{2}+\color{magenta}{2\sqrt{2}})\\
&=&\underline{　4-2\sqrt{2}　}(\,\mathrm{cm}\,)
\end{eqnarray}\)