2023年（令和5年）度神奈川県公立高校入試数学の問題と解説

2023年（令和5年）度の神奈川県公立高校入試、数学の問題と解説です。
大問６つの構成と問題の傾向も昨年度と変わりありません。
（マーク方式採用だからとなめていると痛い目に合うのも変わりません。）
例年通り解法（方針）をいくつか用意してくれているので自分の力を試してみると良いです。

2023年（令和5年）度神奈川県公立高校入試数学の問題

令和５年度の数学の問題です。

⇒　2023年（令和5年）度神奈川県公立高校入試数学の問題ＰＤＦ

白紙のページがありますが、何に使うかは説明不要ですよね。

2023年（令和5年）度神奈川県公立高校入試数学の解説

「問題は問６まであり、」と冊子に書いてくれていますね。
マークシートの使い方は事前に練習しておくようにしましょう。

共通問題なので人によって感じ方は違うと思いますが、
冒頭でも書いておきましたが、「マーク方式だから」という甘い考え方は捨てて下さい。
適当に選んで答えが合う問題ではありません。
逆に解けたと思った後の答えを選び間違えないように注意しましょう。

問１計算問題

軽く解説はしますがマークする記号は自分で探して下さい。
\(\,問１\,\)
（ア）
　\(\hspace{10pt}-1-(-7)\\
=-1+7\\
=\underline{　6　}\)

正の数負の計算は数直線上で考えれば確実です。
（イ）
　\(\hspace{10pt}\displaystyle -\frac{3}{7}+\frac{1}{2}\\
\displaystyle =\frac{-6+7}{14}\\
\displaystyle =\underline{\underline{　\frac{1}{14}　}}\)
分数計算は文字式でも基本は同じです、
通分して分子の計算に集中ですね。
（「分母は一つ」をクセづけても良いくらいですが分けても良いです。）
（ウ）
　\(\hspace{10pt}\displaystyle 12ab^2\times 6a\div (-3b)\\
\displaystyle =-\frac{12ab^2\times 6a}{3b}\\
=\underline{　-24\,a^2\,b　}\)
全体符号の確認が先ですよ。
割り算混じりの計算も分数処理するのは文字式でも同じです。
（エ）
　\(\hspace{10pt}\displaystyle \frac{3x+2y)}{7}-\frac{2x-y}{5}\\
\displaystyle =\frac{5(3x+2y)-7(2x-y)}{35}\\
\displaystyle =\frac{15x+10y-14x+7y}{35}\\
\displaystyle =\underline{\underline{　\frac{x+17\,y}{35}　}}\)
分数計算は文字式でも同じです。
（オ）
無理数の展開と計算です。
　\(\hspace{10pt}\color{red}{(\sqrt{6}+5)^2}\color{blue}{-5(\sqrt{6}+5)}\\
=(\color{red}{6+10\sqrt{6}+25})\color{blue}{-5\sqrt{6}-25}\\
=\underline{　6+5\sqrt{6}　}\)
まとまりがあるのでくふうしてみたいところですが、
　\(\hspace{10pt}\displaystyle (\color{red}{\sqrt{6}+5})^2-5(\color{red}{\sqrt{6}+5})\\
=(\sqrt{6}+5)\{\color{blue}{(\sqrt{6}+5)-5}\}\\
=(\sqrt{6}+5)\times \color{blue}{\sqrt{6}}\\
=6+5\sqrt{6}\)
見直しに違う方法で計算してみる、程度で良いです。

問２方程式や代数の基本確認問題

\(\,問２\,\)
（ア）
因数部分です。
　\(\hspace{10pt}(x-5)(x+3)-2x+10\\
=x^2-2x-15-2x+10\\
=x^2-4x-5\\
=\underline{　(x+1)(x-5)　}\)
ちょっと見方を変えると
　\(\hspace{10pt}(x-5)(x+3)-2x+10\\
=(\color{red}{x-5})(x+3)-2(\color{red}{x-5})\\
=(x-5)(x+3-2)\\
=\underline{　(x-5)(x+1)　}\)
共通因数がすぐに見えるなら良いですが、
たまたま？かと思えるくらいなら展開した方が早いです。
「因数分解しなさい。」というなら因数分解できるはずです。

（イ）
２次方程式を解きます。
　\(\hspace{4pt}7x^2+2x-1=0\)
左辺は因数分解できないので解の公式です。
　\(\begin{eqnarray}
x&=&\frac{-2\pm \sqrt{2^2-4\cdot 7\cdot (-1)}}{2\times 7}\\
&=&\frac{-2\pm \sqrt{4+28}}{14}\\
&=&\frac{-2\pm \sqrt{32}}{14}\\
&=&\frac{-2\pm 4\sqrt{2}}{14}\\
&=&\underline{\underline{　\frac{-1\pm 2\sqrt{2}}{7}　}}
\end{eqnarray}\)
１次の項が偶数なので
　\(\begin{eqnarray}
x&=&\frac{-1\pm \sqrt{1^2-7\cdot (-1)}}{7}\\
&=&\frac{-1\pm \sqrt{8}}{7}\\
&=&\frac{-1\pm 2\sqrt{2}}{7}
\end{eqnarray}\)
とした人もいるでしょう。
もちろん構いません。

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

解の公式を覚えていないと「平方完成して」、
となるのでものすごく時間がかかります。
覚えて使いましょう。（覚え方も簡単です。）

あ、ルートの中の計算は雑にするとミスし易いですよ。

（ウ）
変化の割合を求めます。
関数\(\,y=-2x^2\,\)から
　\(\hspace{4pt}(\,-3\,,\,-18\,)\)
　\(\hspace{4pt}(\,-1\,,\,-2\,)\)
となるので
　\(\begin{eqnarray}
(\,変化の割\,)&=&\frac{　(\,y\,の増分\,)　}{　(\,x\,の増分\,)　}\\
&=&\frac{(-2)-(-18)}{(-1)-(-3)}\\
&=&\frac{16}{2}\\
&=&\underline{　8　}
\end{eqnarray}\)
増分を計算するとき引く方向を間違えないように。
（別々に計算しても良いです。）
値域ではないのでグラフは必要ないですが、
簡単にでもグラフを描くと傾きが正なのか負なのかは確認できます。

（エ）
文字式と連立方程式です。
３桁の数ですが十の位は決まった数なので文字は二つで条件をそろえます。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

文字式をあつかえることは数学の第一歩だと考えて良いです。

百の位を\(\,a\,\)、一の位を\(\,b\,\)とすると元の自然数は、
　\(\hspace{4pt}100a+40+b　･･･①\)
百の位と一の位の数を入れかえた自然数は、
　\(\hspace{4pt}100b+40+a　･･･②\)
\(\,②\,\)は\(\,①\,\)より\(\,396\,\)大きいので
　\(\begin{eqnarray}
100b+40+a&=&100a+40+b+396\\
-99a+99b&=&396\\
a-b&=&-4　･･･③
\end{eqnarray}\)
また、百の位と一の位の数の和は\(\,10\,\)なので
　\(\hspace{4pt}a+b=10　･･･④\)
\(\,③④\,\)から
　\(\hspace{10pt}a=3\,,\,b=7\)
一の位の数を求めるので
　\(\hspace{10pt}b=\underline{　7　}\)

連立方程式を解くのは簡単な加減法で済むので省略しました。

（オ）
分数が自然数の平方となる最も小さな自然数を求めます。
　\(\hspace{10pt}\displaystyle \frac{3780}{n}　･･･①\)
平方数が小さくなるのではなく最小の\(\,n\,\)を求めます。
分子を素因数分解すると
　\(\begin{eqnarray}3780&=&2^2\times 3^3\times 5\times 7\\
&=&2^2\times 3^2\times \color{red}{3}\times \color{red}{5}\times \color{red}{7}
\end{eqnarray}\)
平方数になっていない部分は
　\(\hspace{10pt}n=3\times 5\times 7=\underline{　105　}\)

①が平方数になるのはこれだけではありませんが、
\(\,n\,\)が最も小さい（平方数が最も大きい）のはこれだけです。

⇒　平方数とは？かけて、割って平方数にする最小の自然数の見つけ方

ルートを外すときにも同じ考え方になるので、
わかりにくい人はじっくり見ておくと良いです。

問３平面図形と箱ひげ図と１次関数

\(\,問３\,\)
（ア）
平面図形で円があるので相似が多く出て来ます。
問題にある条件を大まかに図示しておきます。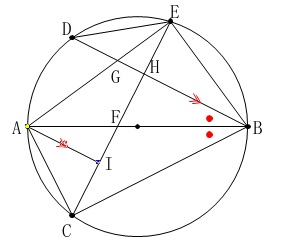相似の証明がありますが、
その前に条件から分かることを少し図に示していきます。
（証明に合わせて書き込んでいっても良いと思います。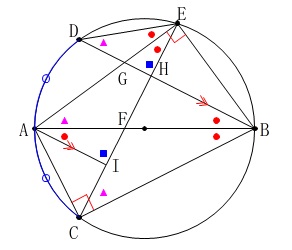）他にもいろいろなことがいえますが、
　条件\(\hspace{10pt}\mathrm{∠ABC=∠ABD}\)
から弧\(\,\mathrm{AD}\,\)と弧\(\,\mathrm{AC}\,\)が等しいことから円周角が等しいところがたくさん。
　条件\(\hspace{10pt}\mathrm{DB}\,\)∥\(\,\mathrm{AI}\,\)
から同位角や錯角が等しくなるところがいくつかあります。
（与えられた条件からいいたそうなことを書き出しておきました。）
(ⅰ)
相似の証明です。
　\(\,\mathrm{△AIF}\,\)∽\(\,\mathrm{△EHG}\,\)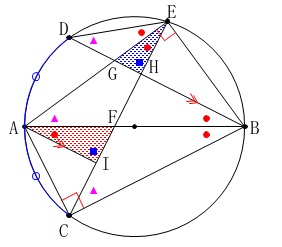図の中で証明は終わっています。
相似条件は「２組の角がそれぞれ等しい。」です。

後は［証明］をうめるように記号を選んでいけば良いだけです。
ただ、［証明］に書かれている角などを図の中で追っていかないと見えてきませんよ。
（ア）は必要か？と思いますけど穴埋めなので探さないといけません。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

相似の証明の目的は「相似条件」をそろえることです。
もちろん、結論とともに文章をまとめますが、
ルールはあるけど形式は決まっていませんので証明の書き方は見ておいて下さい。
（この問題は穴埋めなので何も難しく考えなくて良いですけど。）
(ⅱ)
角度を求めます。
加えられる条件は
　\(\hspace{10pt}\mathrm{∠BDE}=\color{magenta}{35°}\)
　\(\hspace{10pt}\mathrm{∠DBE}=\color{red}{28°}\)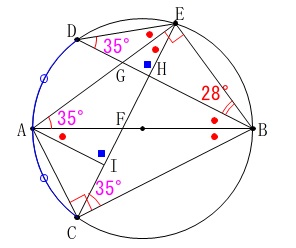円周角が等しいところも書き込みましたが、
加えて線分\(\,\mathrm{AB}\,\)は直径なので
　\(\hspace{10pt}\mathrm{∠AEB=∠ACB}=90°\)
なので三角形の内角の和から\(\,\color{red}{●}\,\)の角度が分かります。
好きなところで良いですが\(\,\mathrm{△ABE}\,\)から
　\(\begin{eqnarray}
\mathrm{∠ABD}&=&90°-(\color{magenta}{35°}+\color{red}{28°})\\
\color{red}{●}&=&27°
\end{eqnarray}\)
（図の\(\,\color{red}{●}\,\)の角度はすべて同じです。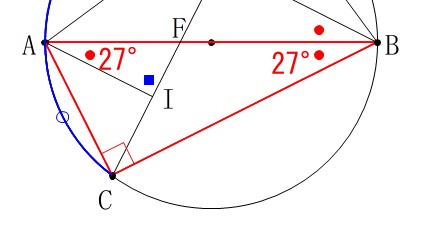）\(\,\mathrm{△ACB}\,\)の内角の和に着目して
　\(\begin{eqnarray}
\mathrm{∠CAI}+27°+27°+90°&=&180°\\
&=&90°-54°\\
&=&\underline{　36°　}
\end{eqnarray}\)

一気に答えは出ませんが、
分かることをたどっていけば答えは出てくるようになっています。
（違う三角形を使う方向でも結果は同じです。）

（イ）
データの問題です。
与えられた資料から箱ひげ図や代表値をみていきましょう。

基本通り資料\(\,10\,\)人のデータを小さい順に並べておきます。
資料１（議案\(\,\mathrm{X}\,\)に賛成した人数）
\(\hspace{4pt}13\,\,14\,\,\color{red}{17}\,\,17\,\,17\,|\,19\,\,21\,\,\color{blue}{23}\,\,24\,\,25\)
資料２（議案\(\,\mathrm{Y}\,\)に賛成した人数）
\(\hspace{4pt}15\,\,19\,\,20\,\,20\,\,20\,|\,24\,\,24\,\,25\,\,26\,\,27\)
(ⅰ)
資料１の箱ひげ図を書けば良いだけです。

最小値\(\,13\,\)、最大値\(\,25\,\)は説明不要として、
偶数データなので中央値が平均値になります。
第１四分位数\(\,\color{red}{17}\,\)、中央値\(\,\color{magenta}{18}\,\)、第３四分位数\(\,\color{blue}{23}\,\)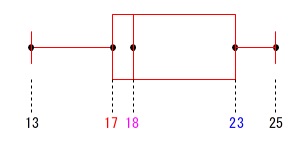答えを選ぶには最小値、最大値、中央値の順に除外していっても良いです。
(ⅱ)
１つ選ぶのは記号で、正しい内容がいくつあるかはわまりません。
すべて選ぶので全部調べますがその前に資料３について触れておきます。
資料３（議案\(\,\mathrm{Z}\,\)に賛成した人数）
平均値\(\,23\,\)、中央値\(\,21\,\)、四分位範囲\(\,6\,\)
平均値が\(\,23\,\)なので賛成した総人数は\(\,\color{red}{230}\,\)人です。
（平均値を\(\,23.0\,\)とみています。）

\(\,\mathrm{A}\,\)
資料２から最頻値は\(\,20\,\)です。○
\(\,\mathrm{B}\,\)
議案\(\,\mathrm{Y}\,\)に賛成した人数は資料２の人数をすべて足すと\(\,\color{blue}{220}\,\)人。
　\(\hspace{4pt}\color{blue}{220}\,＜\,\color{red}{230}\)
議案\(\,\mathrm{Z}\,\)に賛成した人の方が多い。×
\(\,\mathrm{C}\,\)
議案\(\,\mathrm{Y}\,\)に賛成した人の中央値は\(\,22\,\)。
（５番目と６番目\(\,20\,\)と\(\,24\,\)の平均値）
議案\(\,\mathrm{Z}\,\)に賛成した人数の中央値\(\,21\,\)より大きい。○
\(\,\mathrm{D}\,\)
議案\(\,\mathrm{Y}\,\)に賛成した人数の四分位範囲は
　\(\hspace{4pt}25-20\,=\,5\)
これは議案\(\,\mathrm{Z}\,\)に賛成した人数の四分位範囲\(\,6\,\)より小さい。○

選ぶのは\(\,\mathrm{A\,,\,C\,,\,D}\,\)の組み合わせですね。

（ウ）
\(\,\mathrm{B}\,\)さんは一方向に移動していません。
戻る動きをしているので移動した総道のりで考えます。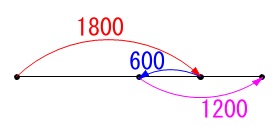学校からいちょう図書館まで\(\,\mathrm{1800\,m}\,\)、
いちょう図書館からかもめ図書館に戻るのに\(\,\mathrm{600\,m}\,\)、
かもめ図書館から駅まで\(\,\mathrm{1200\,m}\,\)、
合計で\(\,\mathrm{3600\,m}\,\)移動しています。

いちょう図書館で\(\,15\,\)分、かもめ図書館で\(\,5\,\)分立ち寄っているので、
移動に費やした時間は\(\,15\,\)分です。

このことから\(\,\mathrm{B}\,\)さんの移動する速さは
　\(\hspace{10pt}\displaystyle \frac{3600}{15}=240\,(\,\mathrm{m}/分\,)\)
この速さは向きに関係なく一定です。

速さが分かったので\(\,\mathrm{B}\,\)さんの移動を表すグラフがかけます。
学校からいちょう図書館まで
　\(\hspace{10pt}\displaystyle \frac{1800}{240}=\frac{15}{2}\,(\,分\,)\)
ここで\(\,15\,\)分立ち寄り、
いちょう図書館からかもめ図書館に引き返すまで
　\(\hspace{10pt}\displaystyle \frac{600}{240}=\frac{5}{2}\,(\,分\,)\)
かもめ図書館から駅まで
　\(\hspace{10pt}\displaystyle \frac{1200}{240}=5\,(\,分\,)\)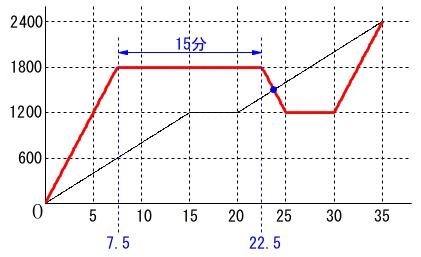\(\,\mathrm{A}\,\)さんとすれ違うのはグラフの交点です。
（おおよその交点の\(\,x\,\)座標は分かるので答えは分かると思います。）

速さが分かればすべての直線の関数が求まります。
交点を含む部分の\(\,\mathrm{A}\,\)さんの移動を表す関数は
２点\(\,(\,20\,,\,1200\,)\,,\,(\,35\,,\,2400\,)\,\)を通るので
　\(\hspace{10pt}\displaystyle y=80\,x-400　･･･①\)
交点を含む部分の\(\,\mathrm{B}\,\)さんの移動を表す関数は、
傾き\(\,-240\,\)で\(\,(\,25\,,\,1200\,)\,\)を通るので
　\(\hspace{10pt}\displaystyle y=-240\,x+7200　･･･②\)
\(\,①②\,\)を連立して、
　\(\begin{eqnarray}
80\,x-400&=&-240\,x+7200\\
320\,x&=&7600\\
x&=&\frac{7600}{320}=23.75
\end{eqnarray}\)
つまり、\(\,16\,\)時\(\,23\,\)分から\(\,16\,\)時\(\,25\,\)分までの間ですれ違います。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

２点を通る直線の求め方は分かると思いますが、
特に神奈川県の公立入試に対応させるには、
短時間で求められるようになっておくことを強くお勧めします。

問３はまだあります。
相変わらずボリュームすごい。
（エ）
台形内部の面積比です。
条件が多いので方針がいくつも出てきて迷いそう。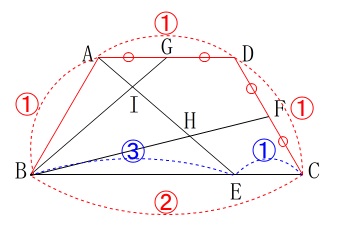問題にある条件を図に示してあります。
問題文を読みながら確認して下さい。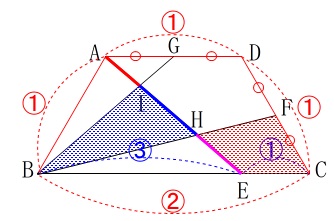求めたいのは三角形\(\,\mathrm{BHI}\,\)と四角形\(\,\mathrm{CFHE}\,\)の面積比ですが、
方針は人によってかなり違ってきそうです。
共通して求めたい線分比は普通にみて
　\(\hspace{4pt}\mathrm{AI:IH:HE}\)
でしょう。

方針すべてを説明すると先に進めないので、
図形的な意味を取るためにも分かり易い補助線を引いておきます。

四角形\(\,\mathrm{ABCD}\,\)は半円の中にあります。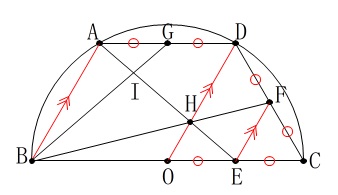円周角を使いたいのではありません。
正三角形と平行線を見つけて欲しいのです。
線分\(\,\mathrm{BC}\,\)の中点を中心\(\,\mathrm{O}\,\)とする円を描くと、
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DO}\,\)∥\(\,\mathrm{FE}\,\)
このとき交点\(\,\mathrm{H}\,\)は\(\,\mathrm{DO}\,\)上にあるのか？
と疑問に感じた人はよく考えています。
ただ、点\(\,\mathrm{H}\,\)は\(\,\mathrm{DO}\,\)上にあります。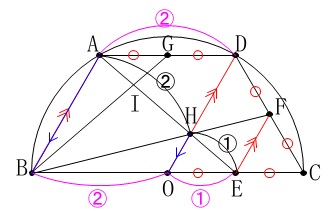この問題にチャレンジしている段階で説明が必要かわかりませんが、
相似比から\(\,\mathrm{AB}\,\)∥\(\,\mathrm{OH}\,\)で、ひし形だから\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DO}\,\)です。
点\(\,\mathrm{O}\,\)は同じ点だから\(\,\mathrm{H}\,\)は\(\,\mathrm{DO}\,\)上にあります。
また、中点連結定理から線分\(\,\mathrm{EF}\,\)も並行なので
　　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DO}\,\)∥\(\,\mathrm{FE}\,\)
となります。

ここから三角形の面積を比で表していっても答えは出ます。
（長さが与えられていないので円の半径を適当に決めて具体的な面積でも良いです。）
一応いろいろな方針が立てられるように、
分かることをいくつか挙げておきます。

四角形\(\,\mathrm{CFHE}\,\)の面積は、
\(\,\mathrm{△EHF}\,\)を等積移動させると\(\,\mathrm{△EOF}\,\)と等しいので、
\(\,\mathrm{△OFC}\,\)と等しい。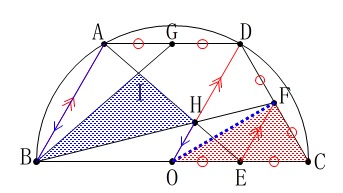\(\,\mathrm{△OBF}\,\)と\(\,\mathrm{△OCF}\,\)は底辺が半径で等しいので
　\(\,\mathrm{△OBF=△OCF}\,\)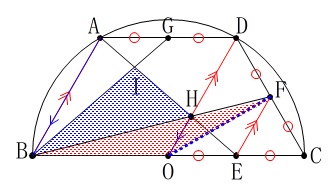今度は点\(\,\mathrm{F}\,\)を平行移動させて
　\(\,\mathrm{△OHF=△OHE}\,\)
となることから
　\(\,\mathrm{△OBF=△BHE}\,\)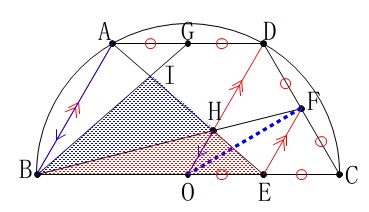つまり、四角形\(\,\mathrm{CFHE}\,\)の面積は、
\(\,\mathrm{△EBH}\,\)と同じになるので求める面積比は
　\(\hspace{10pt}\mathrm{IH:HE}\)
を求めれば良いということです。

他にもが中点連結定理から高さが等しいので底辺を\(\,\mathrm{EF}\,\)とみて
　\(\,\mathrm{△EFH=△EFC}\,\)
なので四角形\(\,\mathrm{CFHE}\,\)の面積は\(\,\mathrm{△EFC}\,\)の２倍です。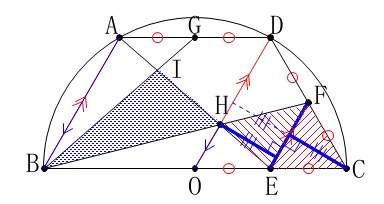このことから三角形の面積比でも答えが出ます。

長さの比についてもいろいろ出てきます。
ついでなので高さについても少しみておきましょうか。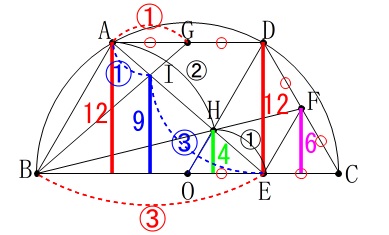線分の長さを表しているのは比です。
後で説明する線分比をみれば、
整数とするため\(\,12\,\)を正三角形の高さとしていることが分かります。

こんな説明なくても問題は解けますが、
図形的な意味を確認しておくと良いですよ。

さて、どういった方法で答えを出しましょうか？
台形の面積や\(\,\mathrm{△EFC}\,\)を基準に考えても良いのですが、
図形的な意味がとれたなら線分比を求めに行けば良いですかね。

線分\(\,\mathrm{AE}\,\)を抜き出すと、
　\(\hspace{4pt}\mathrm{AI:IE}=\color{blue}{①}:\color{blue}{③}\)
　\(\hspace{4pt}\mathrm{AH:HE}=②:①\)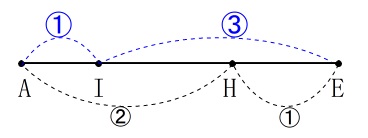それぞれの比の和の公倍数で長さを勝手に決めます。
線分\(\,\mathrm{AE}\,\)を最小公倍数の\(\,\color{red}{12}\,\)とすると
　\(\hspace{4pt}\mathrm{AI:IE}=3:9\)
　\(\hspace{4pt}\mathrm{AH:HE}=8:4\)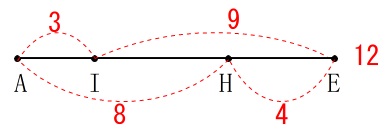このように整数比で分けると分かりやすいです。
このとき線分比は
　\(\hspace{4pt}\mathrm{AI:IH:HE}=\color{red}{3}:\color{red}{5}:\color{red}{4}\)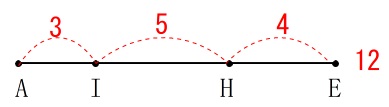よって求める面積比は、
　\(\hspace{10pt}S:T=\underline{　5:4　}\)

今さらだけど、誰もみていないだろうから良いだろう。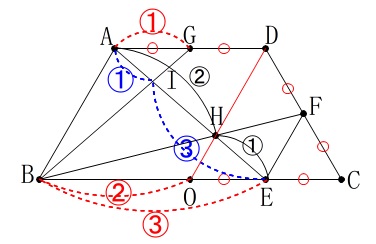正三角形\(\,\mathrm{△ABO}\,\)や\(\,\mathrm{△DOC}\,\)の面積を\(\,1\,\)として、
相似比から、底辺や高さを考えて
　\(\hspace{4pt}\displaystyle \mathrm{△FEC}=\color{red}{\frac{1}{4}}\)
　\(\hspace{4pt}\displaystyle \mathrm{△FBE}=\frac{3}{2}\times \frac{1}{2}=\color{magenta}{\frac{3}{4}}\)
　\(\hspace{4pt}\displaystyle \mathrm{△HBE}=\mathrm{△FBE}\times \frac{2}{3}=\color{magenta}{\frac{3}{4}}\times \frac{2}{3}=\frac{1}{2}\)
　\(\hspace{4pt}\displaystyle \mathrm{△FHE=△FBE-△HBE}=\frac{3}{4}-\frac{1}{2}=\color{red}{\frac{1}{4}}\)
ここでも\(\,\mathrm{△FEC}\,\)と\(\,\mathrm{△FHE}\,\)の面積が等しいことは分かる。
　\(\hspace{4pt}\displaystyle \mathrm{△IBE}=\frac{3}{2}\times \frac{3}{4}=\frac{9}{8}\)
　\(\hspace{4pt}\displaystyle \mathrm{△BHI=△IBE-△HBE}=\frac{9}{8}-\frac{1}{2}=\color{blue}{\frac{5}{8}}\)
よって、
　\(\begin{eqnarray}S:T&=&\color{blue}{\frac{5}{8}}:\left(\color{red}{\frac{1}{4}}+\color{red}{\frac{1}{4}}\right)\\
&=&\frac{5}{8}:\frac{4}{8}\\
&=&\underline{　5:4　}
\end{eqnarray}\)
普通に面積比から足し算引き算をするとこうだよな。

こんなところで時間潰しても仕方ないのに何をやっているんだろう。

次いこう。

問４関数総合

\(\,問４\,\)
関数です。
神奈川県ではおなじみだと思うのですが、
直線の式を求めることに時間をかけていたら攻略不可能です。

先ずは条件がまとめて与えられるので整理していきます。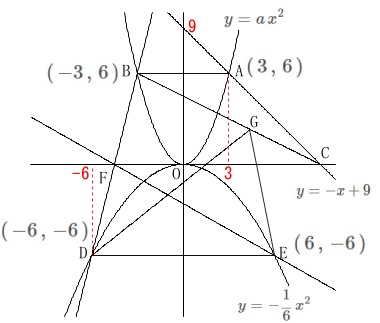当たり前ですがここを抜きにして関数の問題は解けません。
点\(\,\mathrm{A}\,\)は直円\(\,①\,\)上の点で\(\,x\,\)座標が\(\,3\,\)なので
　\(\hspace{10pt}\mathrm{A}\,(\,3\,,\,6\,)\)
点\(\,\mathrm{B}\,\)は点\(\,\mathrm{A}\,\)と\(\,y\,\)座標が同じで
　\(\hspace{10pt}\mathrm{B}\,(\,-3\,,\,6\,)\)
同様に点\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,-6\,\)なので
　\(\hspace{10pt}\mathrm{D}\,(\,-6\,,\,-6\,)\)
　\(\hspace{10pt}\mathrm{E}\,(\,6\,,\,-6\,)\)
あと、切片は\(\,x\,,\,y\,\)ともに書き込んでおくと良いです。

さて、と。
相変わらずだけど、ブレないですねえ。
何本直線出てくるんだ？

（ア）
比例定数を求めます。
曲線\(\,②\,\)は点\(\,\mathrm{A}\,\)を通るので、
\(\,y=a\,x^2\,\)に\(\,(\,3\,,\,6\,)\,\)を代入して
　\(\begin{eqnarray}
6&=&a\times (\,3\,)^2\\
a&=&\underline{\underline{　\frac{2}{3}　}}
\end{eqnarray}\)
（イ）
直線\(\,\mathrm{EF}\,\)の式を求めます。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式を求めるのが苦手というのは関数を捨てるのと同じです。
当然ここでも通用しません。

２点\(\,\mathrm{E\,,\,F}\,\)の座標を求めますが、
点\(\,\mathrm{F}\,\)は直線\(\,\mathrm{DB}\,\)の\(\,x\,\)切片（\(\,x\,\)軸との交点）です。
直線\(\,\mathrm{DB}\,\)を先に求めます。
　\(\hspace{4pt}(\,-6\,,\,-6\,)\)
　\(\hspace{4pt}(\,-3\,,\,6\,)\)
から直線\(\,\mathrm{DB}\,\)の式は
　\(\hspace{10pt}y=4\,x+18\)
\(\,y=0\,\)として\(\,\mathrm{F}\,\)の\(\,x\,\)座標を求めると
　\(\begin{eqnarray}
0&=&4\,x+18\\
x&=&-\frac{9}{2}
\end{eqnarray}\)
よって点\(\,\mathrm{F}\,\)の座標は
　\(\hspace{10pt}\displaystyle \color{red}{\left(-\frac{9}{2}\,,\,0\,\right)}\)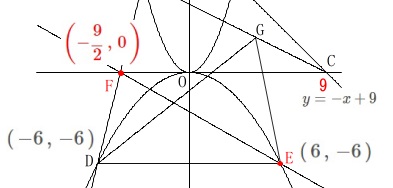このことから直線\(\,\mathrm{EF}\,\)は２点
　\(\hspace{4pt}\displaystyle \left(-\frac{9}{2}\,,\,0\,\right)\)
　\(\hspace{4pt}(\,6\,,\,-6\,)\)
を通るので
　\(\hspace{10pt}\displaystyle y=-\frac{4}{7}\,x-\frac{18}{7}\)

直線\(\,\mathrm{EF}\,\)の式を\(\,y=mx+n\,\)とすると
　\(\hspace{4pt} \displaystyle \underline{\underline{　m=-\frac{4}{7}\,,\,n=-\frac{18}{7}　}}\)

ここは分数計算になるので増加量は\(\,x\,,\,y\,\)別々に計算した方が確実です。
　\(\hspace{4pt}\displaystyle (\,x\,の増加量\,)=6-\left(-\frac{9}{2}\right)=\frac{21}{2}\)
　\(\hspace{4pt}\displaystyle (\,y\,の増加量\,)=-6-0=-6\)
これから傾き\(\,m\,\)は
　\(\hspace{10pt}\displaystyle m=\frac{-6}{\frac{21}{2}}=-6\div \frac{21}{2}=-6\times \frac{2}{21}=-\frac{4}{7}\)
傾きが分かれば\(\,y\,\)切片\(\,n\,\)は点\(\,\mathrm{E}\,\)を代入すれば出てくるので、
自分で計算しておいてください。

（ウ）
座標上での三角形の面積を考える問題です。

文字を使って座標設定することが前提なのか？
いくつか方針が思い浮かぶのですが、
真っ先に思いつくのが会員向けになってしまうところがやっかいです。

まあ、条件を座標上でみておきましょう。
「線分\(\,\mathrm{BC}\,\)上」に点\(\,\mathrm{G}\,\)をとり\(\,\mathrm{△BDG=△DEG}\,\)となるときの、
点\(\,\mathrm{G}\,\)の\(\,x\,\)座標を求めます。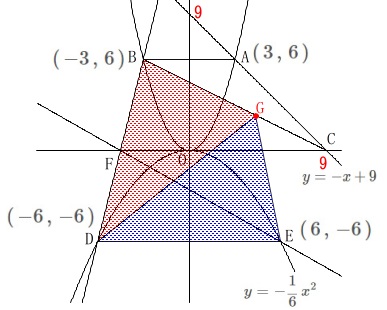座標設定できると少しは楽になりますが、
どちらもやっておきましょう。

（ウ）座標設定する方法

点\(\,\mathrm{G}\,\)の\(\,x\,\)座標を\(\,\color{red}{t}\,\)としますが、
「線分\(\,\mathrm{BC}\,\)上に」なので\(\,-3\,≦\,\color{red}{t}\,≦\,9\,\)です。

点\(\,\mathrm{G}\,\)は直線\(\,\mathrm{BC}\,\)上の点なので、
直線\(\,\mathrm{BC}\,\)の式を求めておくと、
２点\(\,(\,-3\,,\,6\,)\,,\,(\,9\,,\,0\,)\)を通ることから
　\(\hspace{10pt}\displaystyle y=-\frac{1}{2}\,x+\frac{9}{2}\)
点\(\,\mathrm{G}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると\(\,\mathrm{G}\,\)の座標は
　\(\hspace{4pt}\displaystyle \color{red}{\left(\,t\,,\,-\frac{1}{2}\,t+\frac{9}{2}\,\right)}\)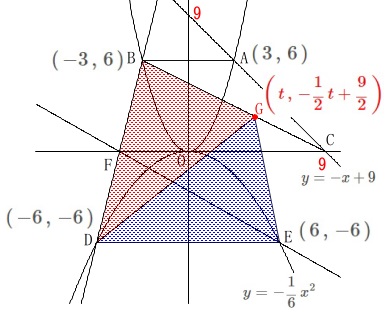文字設定しない場合も後で説明しておきます。

どれから説明しよう？
\(\,\mathrm{△GDE}\,\)の面積が\(\,t\,\)で表しやすいので、
先にやってお行きましょう。
\(\,\mathrm{△GDE}\,\)は底辺\(\,\mathrm{DE}\,\)、高さは\(\,\mathrm{G}\,\)と\(\,\mathrm{D\,,\,E}\,\)の\(\,y\,\)座標の差なので
　\(\begin{eqnarray}
\mathrm{△GDE}&=&\frac{1}{2}\times 12\times \left(\,-\frac{1}{2}\,t+\frac{9}{2}-(-6)\right)\\
&=&6\times \left(\,-\frac{1}{2}\,t+\frac{21}{2}\,\right)\\
&=&-3\,t+63　･･･①
\end{eqnarray}\)
（これ、途中で止めておいた方が後々楽なのですがここでは計算しておきます。）

\(\,\mathrm{△BDG}\,\)の面積は別の方法でも表せますが、
\(\,\mathrm{D}\,\)を平行移動させて表しておきます。
（会員は絶対値で計算して適当な\(\,t\,\)を選べば良いですよ。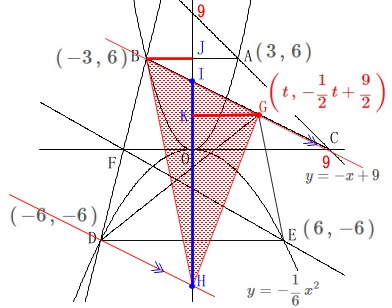）図のように点\(\,\mathrm{D}\,\)を\(\,\mathrm{BC}\,\)と平行に移動させると、
　\(\,\mathrm{△BDG}\,\)=\(\,\mathrm{△BHG}\,\)
点\(\,\mathrm{H}\,\)の座標は直線\(\,\mathrm{DH}\,\)の\(\,y\,\)切片です。
直線\(\,\mathrm{DH}\,\)の式は傾きが直線\(\,\mathrm{BC}\,\)と同じで点\(\,\mathrm{D}\,\)を通るので
　\(\hspace{4pt}\displaystyle y=-\frac{1}{2}\,x-9\)
直線\(\,\mathrm{BC}\,\)の\(\,y\,\)切片\(\,\mathrm{I}\,\)の\(\,y\,\)座標は\(\,\displaystyle \frac{9}{2}\,\)なので、
底辺\(\,\mathrm{IH}\,\)の三角形とみて
　\(\begin{eqnarray}
\mathrm{△BDG}&=&\mathrm{△BHG}\\
&=&\frac{1}{2}\times \mathrm{IH}\times (\,\mathrm{BJ+GK}\,)\\
&=&\frac{1}{2}\times \frac{27}{2}\times (\,3+t\,)\\
&=&\frac{81}{4}+\frac{27}{4}\,t　･･･②
\end{eqnarray}\)
\(\,①\,\)と\(\,②\,\)が等しくなるときなので
　\(\begin{eqnarray}
-3\,t+63&=&\frac{81}{4}+\frac{27}{4}\,t\\
-12\,t+252&=&81+27\,t\\
39\,t&=&171\\
13\,t&=&57\\
t&=&\underline{\underline{　\frac{57}{13}　}}
\end{eqnarray}\)

なんだかスマートじゃないけど答えは出ます。
ちなみに、３点でできる三角形の面積を求める方法を知っている会員は
　\(\hspace{4pt}\displaystyle \mathrm{△BDG}=\left|\frac{-27t-81}{4}\right|\)
となり答えが２つ出てきますが\(\,t\,\)の範囲の条件で１つに絞れます。
※
絶対値の中は\(\,-3\,≦\,\color{red}{t}\,≦\,9\,\)から\(\,0\,\)以下になるので
　\(\hspace{4pt}\displaystyle \left|\frac{-27t-81}{4}\right|=\frac{27t+81}{4}\)
だけを考えれば良いです。

（ウ）図形的に考えて交点を求める方法

図形的な意味を考えるとまた違った方向に行きます。
点\(\,\mathrm{G}\,\)が条件を満たしているとします。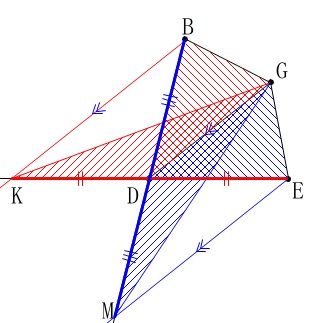どちらでも良いですが、\(\,\mathrm{DG}\,\)と平行な直線を引きます。
点\(\,\mathrm{B}\,\)を通り\(\,\mathrm{DG}\,\)と平行な直線と直線\(\,\mathrm{DE}\,\)との交点を\(\,\mathrm{K}\,\)とすると、
　\(\,\mathrm{△BDG}\,\)=\(\,\mathrm{△KDG}\,\)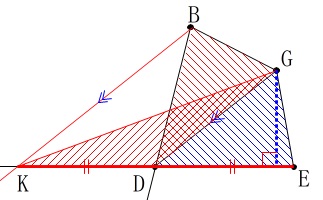高さは共通で面積が等しいので\(\,\mathrm{KD=DE}\,\)となり、
点\(\,\mathrm{K}\,\)の座標は\(\,(\,-12\,,\,-6\,)\,\)となるから、
直線\(\,\mathrm{KB}\,\)の傾き\(\,a\,\)は
　\(\hspace{4pt}\mathrm{K}\,(\,-18\,,\,-6\,)\)
　\(\hspace{4pt}\mathrm{B}\,(\,-3\,,\,6\,)\)
から
　\(\begin{eqnarray}
a&=&\frac{6-(-6)}{-3-(-18)}\\
&=&\frac{12}{15}=\frac{4}{5}
\end{eqnarray}\)
これから直線\(\,\mathrm{DG}\,\)の式は点\(\,\mathrm{D}\,(\,-6\,,\,-6\,)\)を通ることから
　\(\hspace{10pt}\displaystyle y=\frac{4}{5}\,x-\frac{6}{5}\)
点\(\,\mathrm{G}\,\)は直線\(\,\mathrm{DG}\,\)と直線\(\,\mathrm{BC}\,\)との交点なので
　\(\begin{eqnarray}
\frac{4}{5}\,x-\frac{6}{5}&=&-\frac{1}{2}\,x+\frac{9}{2}\\
8x-12&=&-5x+45\\
13x&=&57\\
x&=&\frac{57}{13}
\end{eqnarray}\)
となります。
（座標を設定していれば傾きだけで答えが出ます。）

点\(\,\mathrm{E}\,\)を平行移動しても同じですのでやってみて下さい。

固定されている面積がないのでやりにくい問題だったかもしれません。

問５確率

\(\,問５\,\)
２つのさいころの確率なので樹形図（または表）で終わりますが、
問題の「例」のような場合をいくつか試しておくと良いです。

【操作１】と【操作２】を連続で行った後の結果の確率ですので、
それぞれがどのような移動をするのか試して見ましょう。

で、試して見ると【操作２】の移動で場所\(\,\mathrm{R}\,\)の個数が決まります。
（問題に書いてあるけど念のため）
\(\,\mathrm{P\,,\,Q}\,\)の個数は出る目によって違うので注意。
（ア）
３か所ともブロックの個数が同じになるということは、
３か所ともブロックは２個ずつになるということです。
樹形図で確認しながらみていくと気がつくと思いますが、
さいころの出た目に奇数があったり、同じ数字が出てもダメだと分かります。
ということは、\(\,a\,\)と\(\,b\,\)の候補は２と４だけ。
　\(\,a=2\,,\,b=4\,\)または\(\,a=4\,,\,b=2\,\)
しかないので２つのさいころの目の出方は３６通りなので
　\(\hspace{10pt}\displaystyle \frac{2}{36}=\underline{\underline{　\frac{1}{18}　}}\)
樹形図で確認しておくと確実です。
（\(\,a=6\,\)または\(\,b=6\,\)も偶数だけど、０になる場所ができる。）
（イ）
少なくとも１か所のブロックが０個になる確率です。
（「少なくとも」なので\(\,\color{red}{普通なら}\,\)余事象ですね。）

少なくとも１か所のブロックが０個なので、
０個になるのは１か所か２か所です。（３か所とも０個はない。）
１か所０個になる確率と２か所０個になる確率を足せば良いのです。
※
逆に余事象で考えると０個になる場所がない確率を１から引けば求まりますが、
簡単にですがあとで説明します。

（ア）で樹形図を書いたならどちらでも大した差はないでしょう。
ただし、２か所が０個になるのは\(\,a=6\,,\,b=6\,\)の一通りしかないので、
１か所０個になる場合を考えます。

\(\,a=6\,\)のとき必ず\(\,\mathrm{P}\,\)は０個になります。
また、\(\,a\,,\,b\,\)同じ数字のとき\(\,\mathrm{Q}\,\)は０個になるので、
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \,1\, & \,2\, & \,3\, & \,4\, & \,5\, & \,6\, \\ \hline
\,1\, & ○ & & & & & ○ \\ \hline
2 & & ○ & & & & ○ \\ \hline
3 & & & ○ & & & ○ \\ \hline
4 & & & & ○ & & ○ \\ \hline
5 & & & & & ○ & ○ \\ \hline
6 & ○ & ○ & ○ & ○ & ○ &○○ \\ \hline
\end{array}\)
答え　\(\hspace{10pt}\displaystyle \frac{16}{36}=\underline{\underline{　\frac{4}{9}　}}\)

余事象で考えると０個になる場所がどこにもないのは、
出目に６がなく、１から５の中から違う数字が出たときで、
　\(\hspace{10pt}5\times 4=20\)通り
よって、
　\(\hspace{10pt}\displaystyle 1-\frac{20}{36}=\frac{16}{36}=\frac{4}{9}\)

どっちでも良いです。

問６空間図形（円錐と線分）

\(\,問６\,\)
空間図形の問題です。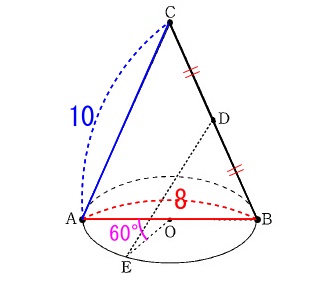※長さの単位は\(\,\mathrm{cm}\,\)です。
問題にある条件くらいは図に書き込みましょう。

ここは簡単に済ませますので分からない場合は質問して下さい。
（決して飽きて、、、疲れた、、、訳ではないです。）
（ア）
円すいの「表面積」を求めます。
底面の円周とおうぎ形の弧は\(\,\color{blue}{8\,\pi}\)で等しく、
おうぎ形の面積は
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 8\,\pi\times 10=40\,\pi\)
底面の円の面積は
　\(\hspace{10pt}\displaystyle \pi\,(\,4\,)^2=16\,\pi\)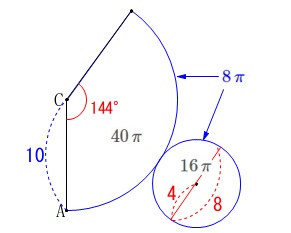求める表面積\(\,S\,\)は
　\(\begin{eqnarray}
S&=&40\,\pi+16\,\pi\\
&=&\underline{　56\,\pi　}\,(\mathrm{cm^2})
\end{eqnarray}\)

⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

おうぎ形の面積は中心角を出してから比例計算で求めて良いですよ。

（イ）
２点\(\,\mathrm{D\,,\,E}\,\)間の距離を求めますが、
線分\(\,\mathrm{DE}\,\)は円すいの内部にあります。

直角三角形を利用したいので補助線を引きます。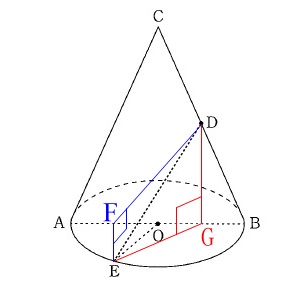\(\,\mathrm{△DEF}\,\)を選びます。
底面を抜き出すと辺\(\,\mathrm{EF}\,\)の長さが出てきます。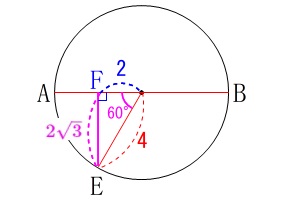三角定規の１辺になるので
　\(\hspace{10pt}\mathrm{FE}=\color{magenta}{2\sqrt{3}}\)

次に\(\,\mathrm{FD}\,\)の長さが欲しいので\(\,\mathrm{△CAB}\,\)を抜き出します。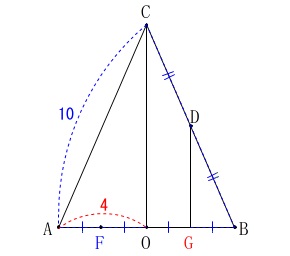三平方の定理から
　\(\begin{eqnarray}
\mathrm{CO^2+\color{red}{AO}^2}&=&\mathrm{\color{blue}{AC}^2}\\
\mathrm{CO^2}+\color{red}{4}^2&=&\color{blue}{10}^2\\
\mathrm{CO^2}&=&84\\
\mathrm{CO}&=&\pm 2\sqrt{21}
\end{eqnarray}\)
辺の長さだから
　\(\hspace{10pt}\mathrm{CO}=\color{magenta}{2\sqrt{21}}\)
また、\(\,\mathrm{OB}\,\)の中点を\(\,\mathrm{G}\,\)とすると中点連結定理から
　\(\hspace{10pt}\mathrm{DG}=\color{green}{\sqrt{21}}\)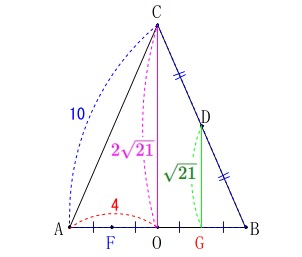さらに点\(\,\mathrm{F\,,\,G}\,\)の位置はそれぞれ\(\,\mathrm{AO\,,\,BO}\,\)の中点なので、
　\(\,\mathrm{FG}=\color{red}{4}\,\)

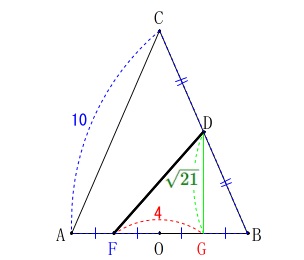
直角三角形\(\,\mathrm{DFG}\,\)から
　\(\begin{eqnarray}
\mathrm{FD^2}&=&\mathrm{\color{green}{DG}^2+FG^2}\\
\mathrm{FD^2}&=&(\color{green}{\sqrt{21}})^2+\color{red}{4}^2\\
&=&37\\
\mathrm{FD}&=&\pm \sqrt{37}
\end{eqnarray}\)
長さだから\(\,\mathrm{FD}\,＞\,0\,\)なので
　\(\hspace{10pt}\mathrm{FD}=\sqrt{37}\)

ここで直角三角形\(\,\mathrm{DEF}\,\)を抜き出します。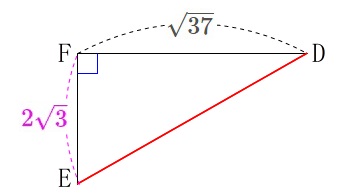またまた三平方の定理から
　\(\begin{eqnarray}
\mathrm{DE^2}&=&\mathrm{EF^2+FD^2}\\
&=&(\color{magenta}{2\sqrt{3}})^2+(\sqrt{37})^2\\
&=&12+37\\
&=&49\\
\mathrm{DE}&=&\pm 7
\end{eqnarray}\)
（もういいでしょう。）
　\(\hspace{10pt}\mathrm{DE}=\underline{　7　}(\mathrm{\,cm\,})\)

直角三角形\(\,\mathrm{DEG}\,\)を利用しても同じですよ。
線分\(\,\mathrm{FD}\,\)を求めるか\(\,\mathrm{EG}\,\)を求めるかの違いだけですので、
自分で計算してみて下さい。
　\(\hspace{10pt}\mathrm{EG}=2\sqrt{7}\)
　\(\hspace{10pt}\mathrm{DG}=\sqrt{21}\)
　\(\hspace{10pt}\displaystyle \mathrm{DE}=\sqrt{28+21}=\underline{　7　}\)

言っておきます。
長々と図を書いて説明していますが、
自分で図の中で処理すればすぐに終わりますから。
（う）も同様にそれ程時間はかかりません。

（ウ）
長さを求めます。
「最も短くなる」だから直線です。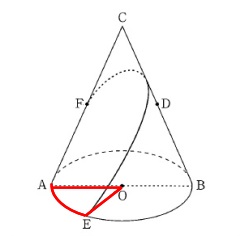円すいの展開図で考えます。
ただ、点\(\,\mathrm{E}\,\)からぐるっと回って\(\,\mathrm{F}\,\)までの部分には、
弧\(\,\mathrm{AE}\,\)の\(\,60°\,\)部分がなくなっていることに注意しましょう。

底面の弧\(\,\mathrm{ABE}\,\)は\(\,300°\,\)分で
　\(\hspace{4pt}\,\displaystyle 8\,\pi\times \frac{300}{360}=\color{blue}{\frac{20}{3}\,\pi}\,\)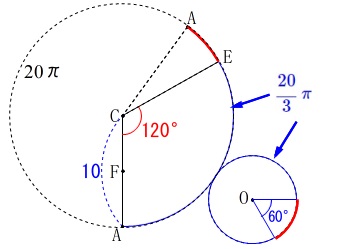側面のおうぎ形の弧\(\,\mathrm{AE}\,\)も\(\,\displaystyle \color{blue}{\frac{20}{3}\,\pi}\,\)で、
中心\(\,\mathrm{C}\,\)、半径\(\,10\,\)の円周は\(\,20\,\pi\,\)だから
　\(\hspace{10pt}\displaystyle \mathrm{∠ECF}=360^{\circ}\times \frac{1}{3}=\color{red}{120°}\)
つまり求めたい距離は\(\,\mathrm{AC}\,\)の中点\(\,\mathrm{F}\,\)から\(\,\mathrm{E}\,\)までの距離です。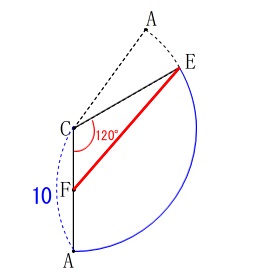三角定規が作れる角度なので後は楽です。
図の垂線\(\,\mathrm{ET}\,\)を引くと三角定規ができるので
　\(\hspace{10pt}\displaystyle \mathrm{ET}=\color{magenta}{5\sqrt{3}}\)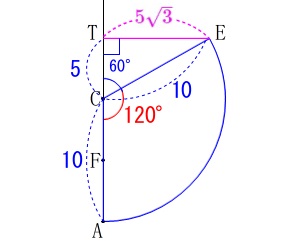点\(\,\mathrm{F}\,\)は\(\,\mathrm{AC}\,\)の中点なので、
　\(\hspace{10pt}\displaystyle \mathrm{TF}=\color{blue}{10}\)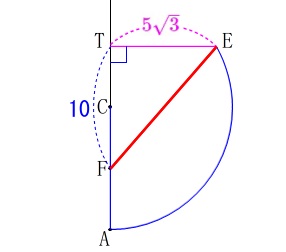三平方の定理から
　\(\begin{eqnarray}
\mathrm{EF^2}&=&\mathrm{TF^2+TE^2}\\
&=&10^2+(5\sqrt{3})^2\\
&=&100+75\\
&=&175\\
\mathrm{EF}&=&\pm 5\sqrt{7}
\end{eqnarray}\)
よって求める線の長さは
　\(\hspace{10pt}\displaystyle \underline{　5\sqrt{7}　}\,(\,\mathrm{cm}\,)\)