2023年（令和5年）度埼玉県公立高校入試の数学の問題と解説

2023年（令和5年）度埼玉県公立高校入試の数学の問題と解説です。
学校選択問題の解説は別にしますので、先ずは一般問題を見ておいて下さい。
数学を得点源にできる人にとっては物足りなく感じるかもしれませんが、
バランスの良い問題構成なので総確認にはお勧めです。

2023年（令和5年）度埼玉県公立高校入試の数学【一般問題】の問題

表示の注意書きにある通り問題は４問あります。

⇒　2023年（令和5年）度埼玉県公立高校入試の数学【一般問題】の問題ＰＤＦ

注意書きの２(3)に書いてあることは必ず読んでおきましょう。
ここは対策ページではないので言わなくて良いことですが、
これを利用することが対策の１つです。

2023年（令和5年）度埼玉県公立高校入試の数学【一般問題】の解説

問題のページ数は多く感じますが、
実にシンプルに作られた総合問題です。

偏りも少なく幅広く各分野の基礎を的確に問われます。
徹底した基礎の確認問題なので解説は簡単に済ませます。

第１問小問集合

\(\,\large{1}\,\)
広い範囲の基礎確認小問集合で全部で１６題あります。

ここの重要性は後でまとめますので早速進めましょう。
(1)
　\(\hspace{10pt}7x-3x\\
=\underline{　4x　}\)
同類項をまとめるだけです。
(2)
　\(\hspace{10pt}4\times (-7)+20\\
=-28+20\\
=\underline{　-8　}\)
　
暗算でもできる計算ですがミスは大きいですよ。
(3)
　\(\hspace{10pt}30xy^2\div 5x\div 3y\\
\displaystyle =\frac{30xy^2}{5x\times 3y}\\
=\underline{　2y　}\)

割り算は文字式でもいつも通り分数計算で処理します。
(4)
　\(\begin{eqnarray}
1.3x+0.6&=&0.5x+3\\
13x+6&=&5x+30\\
8x&=&24\\
x&=&\underline{　3　}
\end{eqnarray}\)

方程式の処理は小数や分数のままでも良いですが整数係数の方が見やすいです。
(5)
　\(\hspace{10pt}\displaystyle \frac{8}{\sqrt{2}}-3\sqrt{2}\\
\displaystyle =\frac{8\sqrt{2}}{2}-3\sqrt{2}\\
=4\sqrt{2}-3\sqrt{2}\\
=\underline{　\sqrt{2}　}\)

無理数計算は分母の有理化、素因数分解はていねいにしましょう。
(6)
　\(\hspace{10pt}x^2-11x+30\\
=\underline{　(x-5)(x-6)　}\)

定数項\(\,30\,\)に注目して、
　\(\color{black}{\fbox{\(\,1\times 30\,\)}}\)、\(\color{black}{\fbox{\(\,3\times 10\,\)}}\)、\(\color{black}{\fbox{\(\,5\times 6\,\)}}\)
後は１次の項の符号をみるだけです。

(7)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 3x+5y=2　･･･①\\
\hspace{4pt} -2x+9y=11　･･･②
\end{cases}\)
連理方程式を解くときは一文字消去が基本です。
　\(\hspace{22pt}6x+10y=4\\
\underline{+)-6x+27y=33}\\
\hspace{46pt}37y=37\\
\hspace{56pt}y=1\)
これを\(\,①\,\)に代入して
　\(\begin{eqnarray}
3x+5\times (1)&=&2\\
3x&=&-3\\
x&=&-1
\end{eqnarray}\)

答え　\(\,\underline{　x=-1\,,\,y=1　}\,\)

先に\(\,y\,\)を消去しても良いですよ。
出てきた解を②に代入して合っているか確認すると見直しになります。
　\(\hspace{4pt}-2\times (-1)+9\times (1)=11\)
代入法でもできますが加減法の方が早いです。
(8)
２次方程式です。
　\(\hspace{4pt}3x^2-5x-1=0\)
因数分解できないので解の公式です。
　\(\begin{eqnarray}
x&=&\frac{-(-5)\pm \sqrt{(-5)^2-4\cdot 3\cdot (-1)}}{2\times 3}\\
&=&\frac{5\pm \sqrt{25+12}}{6}\\
&=&\underline{\underline{　\frac{5\pm \sqrt{37}}{6}　}}
\end{eqnarray}\)

※
ルートの名の「\(\,\cdot\,\)」は掛け算の意味です。
解の公式はその場で導くには時間をかけすぎです。

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

覚え方も難しくはないので覚えて使い倒しましょう。

(9)
標本調査で行われるものを選びます。

答え　\(\,\underline{　ア　と　ウ　}\,\)

全数は無理だろうと思われるものは標本抽出します。
中学生だと実感ないと思いますが国勢調査は全世帯で行います。

(10)
関数と\(\,x\,\)座標が与えられています。
与えられた\(\,x\,\)座標から関数\(\,\displaystyle y=\frac{6}{x}\,\)に代入して
　\(\hspace{4pt}\mathrm{A}\,(\,-6\,,\,-1\,)\,,\,\mathrm{B}\,(\,2\,,\,3\,)\)２点\(\,\mathrm{A\,,\,B}\,\)を通る直線の式は
　\(\hspace{4pt}\displaystyle (傾き)=\frac{3-(-1)}{2-(-6)}=\frac{1}{2}\)
なので\(\displaystyle \,y=\frac{1}{2}\,x+b\,\)とおけて
\(\,\mathrm{A\,,\,B}\,\)のどちらかを代入して\(\,b=2\,\)となります。
　\(\hspace{4pt}\displaystyle \underline{\underline{　y=\frac{1}{2}\,x+2　}}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式は短時間で求める事ができるように練習をしておきましょう。
それと、この問題は親切にグラフの概形を与えてくれています。
本当なら自分ですることですよ。

(11)
２次関数の変域の問題です。
(10)で少し触れていますがグラフを描いて考えましょう。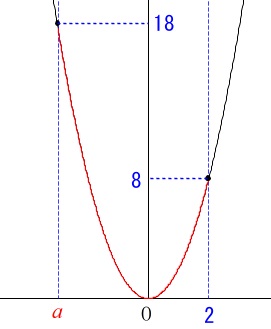最小値は原点の\(\,y=0\,\)と分かりますが、
最大値\(\,18\,\)は\(\,x=2\,\)のときではなく\(\,x=a\,\)のときです。
　\(\begin{eqnarray}
18&=&2\times (\,a\,)^2\\
a^2&=&9\\
a&=&\pm 3
\end{eqnarray}\)
明らかに\(\,a\,\)は負の数なので
　\(\hspace{10pt}\underline{　a=-3　}\)

定義域（\(\,x\,\)の範囲）、値域（\(\,y\,\)の範囲）だけをみててもイメージしにくいですよ。
関数は固定されているのでグラフは描きやすいでしょう。
（グラフは適当で良いです。）

(12)
中点に引かれる線分の長さです。
公式だと瞬間ででますが、
中点連結定理の確認なので平行線でも区切っておきます。頂点\(\,\mathrm{D}\,\)から\(\,\mathrm{AB}\,\)に平行な線分を引いて、
平行四辺形\(\,\mathrm{ABGD}\,\)をつくると、
　\(\hspace{10pt}\mathrm{AD=BG=\color{red}{EH}}=\color{red}{5}\)
　\(\hspace{10pt}\mathrm{GC}=\mathrm{BC-BG}=3\)
また、中点連結定理により
　\(\hspace{10pt}\displaystyle \mathrm{\color{blue}{HF}}=\frac{1}{2}\times \mathrm{GC}=\color{blue}{\frac{3}{2}}\)
よって
　\(\begin{eqnarray}
\mathrm{EF}&=&\mathrm{\color{red}{EH}+\color{blue}{HF}}\\
&=&\color{red}{5}+\color{blue}{\frac{3}{2}}\\
&=&\underline{\underline{　\frac{13}{2}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

頂点\(\,\mathrm{A}\,\)を通り\(\,\mathrm{DC}\,\)に平行な線を引いても同じです。

台形の脚をそれぞれ二等分しているので
　\(\hspace{10pt}\displaystyle \mathrm{EF}=\frac{5+8}{2}=\frac{13}{2}\)
とできた人は早いですね。
※
中点の場合は計算が楽です。
一般的な比に平行線が引かれた場合の公式を、
『超え太郎』－「相似」\(\,\mathrm{No.43}\,\)からまとめていますので会員は確認して下さい。

(13)
確率です。

基本通り樹形図の方が早いのでしっかり取りに行きましょう。
ただし、\(\,50\,\)円硬貨は２つあるので違うものとすることに注意しましょう。
ここでは表で確認しておきます。
表がでたら\(\,○\,\)、裏がでたら\(\,×\,\)とします。
　\(\begin{array}{|c|c|c|c|c|} \hline
　100　 &　 \color{red}{50}　 &　 \color{blue}{50}　 & 　合計　 &　 100円以上　 \\ \hline
○ & ○ & ○ & 200 & ● \\ \hline
○ & ○ & × & 150 & ● \\ \hline
○ & × & ○ & 150 & ● \\ \hline
○ & × & × & 100 & ● \\ \hline
× & ○ & ○ & 100 & ● \\ \hline
× & ○ & × & 50 & 不適 \\ \hline
× & × & ○ & 50 & 不適 \\ \hline
× & × & × & 0 & 不適 \\ \hline
\end{array}\)
樹形図の方が楽です。笑
合計金額が\(\,100\,\)円以上になる確率は
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{5}{8}　}}\)

\(\,100\,\)円硬貨が裏の場合の一通りを見落とさないように、
樹形図はしっかり書いて確認した方が良いです。

(14)
円の面積を求めます。

球を平面で切り取ると切り口が円になることは良いとして、
球の中心から球面までの半径は常に一定だということを忘れずに。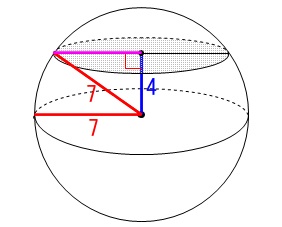三平方の定理から、
切り取られた円の半径\(\,\color{magenta}{r}\,\)はについて
　\(\begin{eqnarray}
\color{magenta}{r}^2+4^2&=&7^2\\
\color{red}{r^2}&=&49-16\\
&=&\color{red}{33}
\end{eqnarray}\)
の関係が成り立ちます。
よって求める円の面積\(\,S\,\)は
　\(\hspace{10pt}S=\pi\,\color{red}{(\,r\,)^2}=\underline{　33\,\pi　}(\,\mathrm{cm^2}\,)\)

半径を\(\,\color{magenta}{r}=\color{magenta}{\sqrt{33}}\,\)とまで求めて計算しても大差ないので構いません。「長さだから」「正の数だから」と書くのがメンドウだからです。
　\(\hspace{10pt}\displaystyle S=\pi\,r^2=\pi\,(\color{magenta}{\sqrt{33}})^2=33\,\pi\)
（といいながら書いているんだから求めても良いのに。）

(15)
２つの関数\(\,y=ax^2\,,\,y=bx+c\)のグラフがあります。
\(\hspace{4pt}a\,,\,b\,,\,c\,\)がすべて同符号のものを選びます。

迷うことなく答えです。　\(\,\underline{　エ　}\,\)

一応説明しておくと、
アは\(\,y\,\)切片\(\,c\,\)だけが負になります。
イは傾き\(\,b\,\)だけが負になります。
ウは比例定数\(\,a\,\)だけが負になります。
エはすべてが負になります。
　\(\hspace{4pt}a\,＜\,0\,,\,b\,＜\,0\,,\,c\,＜\,0\)

大きくアとイは\(\,a\,＞\,0\,\)、ウとエは\(\,a\,＜\,0\,\)と比例定数を分けてみても良いです。
一方で１次関数はアとイは傾き\(\,b\,\)と\(\,y\,\)切片\(\,c\,\)が異符号だと先に省いても良いです。

(16)
ヒストグラムと箱ひげ図です。

ヒストグラムの度数をみて四分位数を大まかにでもみておきましょう。
度数合計が１８なので中央値だけが平均になります。
小さい順にデータを並べたとき
　\(\hspace{4pt}○○○○\color{red}{●}○○○\color{magenta}{○|○}○○○\color{blue}{●}○○○○\)
赤丸\(\,\color{red}{●}\,\)が第１四分位数、青丸\(\,\color{blue}{●}\,\)が第３四分位数になります。データの詳細は分かりませんが、階級値からおおよその箱ひげ図は予想できます。
（四分位数がある階級は分かる。）イの箱ひげ図は、
「第３四分位数が５０以上６０未満の階級にありますが、
ヒストグラムから４０以上５０未満の階級になる」、
から対応していない。
\(\,\mathrm{A}\,\)さんと同じように、
「ヒストグラムから読みとることができる第３四分位数は、」
と書き出すとまとめやすいかもしれませんね。

\(\,\large{1}\,\)だけで６５点分あることは知っておきましょう。
どれだけ基礎を重要とみているか、
どれだけ基礎が重要かを知ると良いです。
※
『覚え太郎』会員は全体通して難しいと感じる問題はないでしょう。
「最大得点法」通り取り組み、満点を取る感覚を手にして下さい。

第２問作図と文字式

\(\,\large{2}\,\)
作図と文字式の説明です。

さらっと済ませましょう。
(1)
４時間後には星は６０°移動します。
回転の中心を探すことになりますが、
できあがりをイメージすれば正三角形の１つの頂点が北極星です。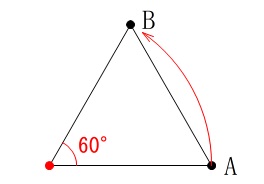回転の中心を探すには、
線分\(\,\mathrm{AB}\,\)の垂直二等分線を描きますが必要ありません。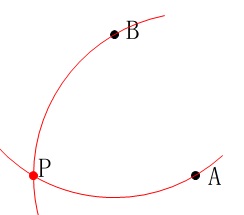正三角形ができるのでコンパスだけで終わりです。
※
会員は会員サイトにある作図問題集『さくっと！』で確認して下さい。

問題に「コンパスと定規を使って」とあるので、
線分\(\,\mathrm{AB}\,\)の垂直二等分線を描いて「定規」を使った方が良いのかなあ。こっちだと回転角が３０°でも１つ円が増えますが使えますね。

(2)
２桁の自然数を文字で表して、問題の条件通り計算すれば良いです。

十のくらいの自然数を\(\,a\,\)、一の位の自然数を\(\,b\,\)とすると
　\(\hspace{4pt}\mathrm{X}=10\,a+b\)
　\(\hspace{4pt}\mathrm{Y}=10\,b+a\)
と表すことができるので\(\,\mathrm{X}\,\)と\(\,\mathrm{Y}\,\)の和は
　\(\begin{eqnarray}
\mathrm{X+Y}&=&(\,10\,a+b\,)+(\,10\,b+a\,)\\
&=&11\,a+11\,b\\
&=&11(\,a+b\,)
\end{eqnarray}\)
\(\,a\,,\,b\,\)ともに自然数なので\(\,\mathrm{X}\,\)と\(\,\mathrm{Y}\,\)の和は\(\,11\,\)の倍数である。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

文字で表すことができればこの手の証明は簡単です。

第３問小数と規則性

\(\,\large{3}\,\)
分数\(\,\displaystyle \frac{1}{n}\,\)の値を小数でみます。
　\(\begin{array}{|c|c|} \hline
　n　 &　 \displaystyle \frac{1}{n}\,の値　 \\ \hline
2 & 0.5 \\ \hline
3 & 0.33333\cdots \\ \hline
4 & 0.25 \\ \hline
5 & 0.5 \\ \hline
6 & 0.16666\cdots \\ \hline
7 & 0.14285714285714\cdots \\ \hline
8 & 0.125 \\ \hline
9 & 0.11111\cdots \\ \hline
10 & 0.1 \\ \hline
\end{array}\)
問題に与えられている表ですが書いておきました。

\(\color{black}{\fbox{　イ　}}\)が難しく思えるかもしれませんが、
推測でも良いですよ。
分母の素因数が\(\,2\,\)と\(\,5\,\)だけのとき割り切れるのです。
(1)
ア
偶数でも\(\,\displaystyle \frac{1}{n}\,\)が無限小数になる\(\,n\,\)は表中から選べば良いので、
　\(\hspace{4pt}\displaystyle \frac{1}{6}=0.1666\cdots \,\)
なので
　\(\hspace{4pt}n=\color{black}{\fbox{　6　}}\)
イ
\(\,n\,\)が２桁の奇数のときは\(\,\displaystyle \frac{1}{n}\,\)は無限小数になる、の「反例」を探します。

反例は１つで良いのですが、会話文から
\(\color{black}{\fbox{　イ　}}\)は\(\,21\,\)から\(\,31\,\)までの奇数なので一つしかありません。

６個の奇数について割り算しても良いのですが、
\(\,\displaystyle \frac{1}{n}\,\)が有限小数になる\(\,n\,\)を素因数分解してみると
　\(\hspace{4pt}2\,,\,4\,,\,5\,,\,8\,,\,10\,,\,16\,,\,20\,\)
⇒\(\hspace{4pt}\,2\,,\,2^2\,,\,5\,,\,2^3\,,\,2\times 5\,,\,2^4\,,\,2^2\times 5\,\)

次にくるのは\(\,5^2\,\)で条件を満たしています。
　\(\hspace{4pt}\displaystyle \frac{1}{25}=0.04\)

答え　\(\color{black}{\fbox{　25　}}\)

試しにもっと大きい数で試して見て下さい。
割り切れますから。（ここでは条件付きです。）

(2)
小数第\(\,50\,\)位の数を求めます。
多少時間かかるけど割り算を続けても答えが出るところが良いですね。

まあ、割り算を続けているうちに規則性に気がつくのですが、
そこからが問題です。
　\(\hspace{4pt}\displaystyle \frac{1}{7}=0.|\color{red}{142857}|\color{blue}{142857}|14\cdots \)

小数第\(\,1\,\)位から小数第\(\,6\,\)位までの数字か繰り返されています。
つまり周期が\(\,6\,\)の規則になっています。
　\(\hspace{4pt}50=6\times 8+2\)
小数第\(\,50\,\)位は\(\,6\,\)個の数字を\(\,8\,\)回繰り返したあとの二つ目の数字です。

答え　\(\color{black}{\fbox{　4　}}\)

割り算しなくても問題に循環している小数があるので答えは出ています。

第４問空間図形

\(\,\large{4}\,\)
直方体の問題です。
空間図形は平面で、ですね。

条件は問題にある通りです。※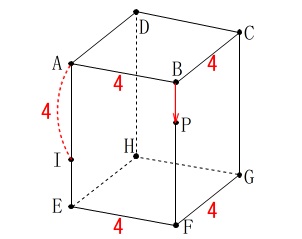
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。
(1)
つながった線分の和が最も短くなるのは直線になるときです。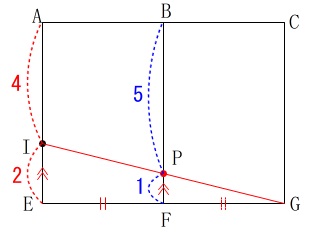中点連結定理から
　\(\hspace{10pt}\displaystyle \mathrm{PF}=\frac{1}{2}\,\mathrm{IE}\,=\,\color{blue}{1}\)
となるので
　\(\hspace{10pt}\mathrm{IP}=\mathrm{BF-PF}=\color{blue}{5}\)
点\(\,\mathrm{P}\,\)は毎秒\(\,\mathrm{1}\,\)で動くのでそのまま答えです。

答え　\(\underline{　5　}(\,秒後\,)\)
(2)
二等辺三角形の証明ですが(1)でみた平面をみれば明らかでしょう。\(\,\mathrm{△ABP}\,\)と\(\,\mathrm{△CBP}\,\)が合同であることをいえば終わりです。
合同条件は「２組の辺とその間の角がそれぞれが等しい。」です。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

図形の証明は図の中で完成させておきましょう。
合同の証明の書き方は合同条件が書かれていれば、
決まりはありませんので書きやすい方法で良いです。
（記号の順序などはルールがあります。）

「合同な図形の対応する辺は等しいので、
　\(\hspace{10pt}\mathrm{AP=CP}\)
なので\(\,\mathrm{△APC}\,\)は二等辺三角形になる。」
を証明の最後に加えておくことを忘れずにしましょう。

(3)
『表面積』を求めます。
『表面積』なので何をするかは分かりますね。
ピンとこない人は『覚え太郎』を一回りしてきて下さい。

\(\,4\,\)秒後に点\(\,\mathrm{P}\,\)は\(\,\mathrm{I}\,\)と同じ高さにいます。２つに切られた立体で大きいのは下側の立体です。
（面\(\,\mathrm{DEFC}\,\)で切られたとき半分です。）

求める立体は６つの面でできています。
　長方形\(\hspace{10pt}\mathrm{DIPC}(S_1)\,,\,\mathrm{IEFP}(S_2)\,,\,\mathrm{DHGC}(S_3)\)
　正方形\(\hspace{10pt}\mathrm{EFGH}(S_4)\,\)
　台形\(\hspace{10pt}\mathrm{DIEH}(S_5)\,,\,\mathrm{CPFG}(S_6)\)
の６つです。

先ずは長方形からみて行きます。　\(\hspace{10pt}S_2=2\times 4=\color{red}{8}\)
　\(\hspace{10pt}S_3=6\times4=\color{red}{24}\)
長方形\(\,\mathrm{DIPC}\,\)は\(\,\mathrm{CP}\,\)の長さが必要なので分けてみます。
面\(\,\mathrm{BFGC}\,\)を抜き出して見るとわかりやすいです。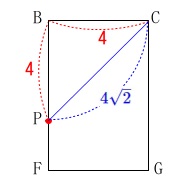線分\(\,\mathrm{CP}\,\)は正方形の対角線になるので
　\(\hspace{10pt}\mathrm{CP}=\color{blue}{4\sqrt{2}}\)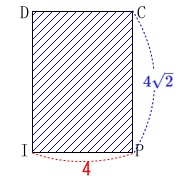切り口になっている長方形ですね。
　\(\hspace{10pt}S_1=4\times 4\sqrt{2}=\color{red}{16\sqrt{2}}\)
次に底面になっている正方形です。　\(\hspace{10pt}S_4=4\times 4\,=\,\color{red}{16}\)
残りの２つの台形は同じ面積です。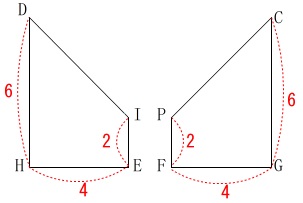切り取られた立体の展開図は６つをつなげたものになります。
　\(\hspace{10pt}\displaystyle S_5=S_6=\frac{6+2}{2}\times 4=\color{blue}{16}\)
求める面積\(\,S\,\)はすべての面積の和で、
　\(\begin{eqnarray}
S&=&S_1+S_2+S_3+S_4+S_5+S_6\\
&=&\color{red}{16\sqrt{2}}+\color{red}{8}+\color{red}{24}+\color{red}{16}+\color{blue}{16}+\color{blue}{16}\\
&=&\underline{　80+16\sqrt{2}　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)