2018年度北海道公立高校入試大問4(裁量問題3)関数の解説

2018年（平成30年)度に北海道で行われた公立高校入試大問4(裁量問題3)の解説です。
大問4は関数の基本、比例定数や値域と面積計算を含んだ問題です。
座標上で文字をあつかうことになれていれば、最初から最後まですぐに終わります。

⇒　北海道2018年数学問題

変域を求めるときの基本作業

問1は変域を求める問題です。

中学の間は変域の名前は、
　\(\,x\,\)の変域　\(\,y\,\)の変域
で良いです。

ただ、高校では
　\(\,x\,\)の変域を「定義域（ていぎいき）」
　\(\,y\,\)の変域を「値域（ちいき）」
といいますので高校になったら確実に覚えておくようにしましょう。
これをわかっていないことだけで、数学で苦労している高校生が多いのでできれば中学生の間に覚えておくと良いです。

さて、変域を求める前にやることをやっておきましょう。
関数も図形と同じ作業が重要で、条件を座標（グラフ）上に書き込むことです。

最初の段階では条件は
　関数は\(\,y=ax^2\,\)
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-2\,\)
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,4\,\)
だけです。
問1は\(\,y=ax^2\,\)の\(\,a\,\)が\(\,a=2\,\)の場合です。
この条件は問1だけの可能性があります。

問題が続く場合は\(\,a=2\,\)とは限らないので注意しておきましょう。

関数の比例定数が決まっていなかったのでグラフの点の\(\,y\,\)座標がわかっていませんでしたが、
\(\,a=2\,\)であるなら決まります。

　\(\,y=2x^2\,\)において

　\(\,x=-2\,\)のとき
　\(\,y=2\times (-2)^2=8\,\)

なので　\(\,\mathrm{A}\,(\,-2\,,\,8\,)\,\)

　\(\,x=4\,\)のとき
　\(\,y=2\times (4)^2=32\,\)

なので　\(\,\mathrm{B}\,(\,4\,,\,32\,)\,\)
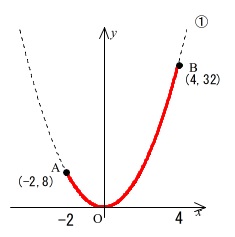このグラフを書くことで最小値を間違えることがなくなります。

　\(-2≦x≦4\)
において最大値は間違えません。
　\(\,y=32\,\)です。

最小値を\(\,y=8\,\)とするミスをする場合がありますので、
簡単なグラフで良いので書いて定義域（\(\,x\,\)の変域）で切っておきましょう。

最小値は原点の\(\,y=0\,\)です。

よって\(\,y\,\)の変域は　\(\,\underline{　0≦y≦32　}\,\)

変化の割合の求め方確認

問2　ここで\(\,a=2\,\)ではなくなっているので、問1の条件は忘れましょう。
せっかくグラフを書いたのに、という気持ちはよくわかります。
私は書かなくてもわかるけど説明のために書き直しているのですから、もっとたいへんです。笑

でも問題を解くときは手書きでささっとすむので何の苦もありません。

最初の条件処理のときにやりませんでしたが、
　\(\,y=ax^2\,\)において、
\(\,x=-2\,\)のとき\(\,y=a\times (-2)^2=4a\,\)です。
\(\,x=4\,\)のとき\(\,y=a\times　(4)^2=16a\,\)です。

本来ならこのように未定係数ごと点の座標を表しておくと最後までささっとすむのですが少しずつ慣れるために順をおって説明します。
問題が誘導してくれるので利用させて頂きましょう。

　\(\,y=ax^2\,\)において、
　\(\,\mathrm{A}\,(\,-2\,,\,4a\,)\,\)
　\(\,\mathrm{B}\,(\,4\,,\,16a\,)\,\)
なので直線\(\,\mathrm{AB}\,\)の傾きは
　\(\displaystyle \,\mathrm{AB}の傾き=\frac{　y\,の増加量　}{　x\,の増加量　}\,\)

直線（1次関数）の場合は傾きと変化の割合は一致します。

会員向け説明なので簡単に済ませますが、
　座標2つを縦に並べて下から上を引いたもの
がそれぞれの増加量です
　
　\(\,(\,-2\,,\hspace{8pt} 4a\,)\,\)
　\(\,(\hspace{10pt} 4\,,\,16a\,)\,\)

下から上を引きます。
「傾きが\(\,1\,\)となるとき」と問題に与えてくれているので

　\(\begin{eqnarray}
\displaystyle \frac{16a-4a}{4-(-2)}&=&1\\
\displaystyle \frac{12a}{6}&=&1\\
2a&=&1\\
a&=&\underline{　\frac{1}{2}　}
\end{eqnarray}\)

文字の設定と注意点

問3は\(\,a=1\,\)のときです。
問1とも問2とも違います。

こういう問題は誘導されてなくて、単発で考える問題なので切り替えが必要です。

ただ、小問集合的な問題になるので簡単な問題か、または極端に難しい問題かに分かれます。
ほとんどは簡単な方なので、座標（グラフ）を書いて見るとすぐに終わります。

どれくらい簡単か見てみます。
座標にわかることを書き込むことからです。
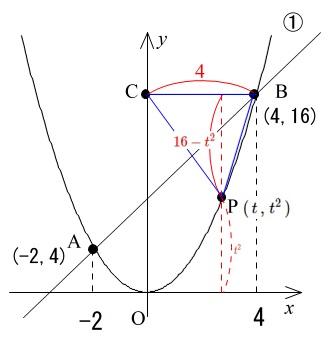書き込んだことはしたの下の条件の赤字で示した部分です。

　\(\,a=1\,\)　なので①は　\(\,y=x^2\,\)
　\(\,\mathrm{A}\,(\,-2\,,\,4\,)\,\)
　\(\,\mathrm{B}\,(\,4\,,\,16\,)\,\)

　\(\,\mathrm{C}\,\)は\(\,\mathrm{B}\,\)と\(\,y\,\)座標が同じなので
　\(\color{red}{\mathrm{BC}=4}\)

　\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
　\(\,\mathrm{P}\,(\,t\,,\,t^2\,)\)

　\(\,△\mathrm{BCP}=14\,\)

　\(\,\color{blue}{-2＜t＜4}\,\)

図を見ればすぐにわかるでしょう。

\(\,△\mathrm{BCP}\,\)の底辺を\(\,\mathrm{BC}\,\)とすると高さは\(\,\color{red}{16-t^2}\,\)となるので、
　\(\displaystyle \frac{1}{2}\times 4 \times (16-t^2)=14\)

これを解けば答えです。
座標でもなく、\(\,t\,\)の値を出すだけなので\(\,t\,\)の方程式を解いて、
　\(\,\color{blue}{-2＜t＜4}\,\)　
の範囲にある\(\,t\,\)が答えです。

　\(\begin{eqnarray}
\displaystyle \frac{1}{2}\times 4 \times (16-t^2)&=&14\\
2(16-t^2)&=&14\\
16-t^2&=&7\\
-t^2&=&7-16\\
-t^2&=&-9\\
t^2&=&9\\
t&=&\pm 3
\end{eqnarray}\)
　　\(\,-2＜t＜4\,\)　より　\(\,t=\underline{　3　}\,\)

問題が「点\(\,\mathrm{P}\,\)の座標」と聞いてきたら、
　\(\,(\,3\,,\,9\,)\,\)
のように\(\,x\,\)座標と\(\,y\,\)座標と両方書いて下さい。

　『\(\,x\,\)座標』なら\(\,x\,\)座標だけで良いです。
　『\(\,y\,\)座標』なら\(\,y\,\)座標だけで良いです。

しかし、『座標』と聞かれたら
　\(\,x\,\)座標、\(\,y\,\)座標の両方書かなければいけません。

グラフに情報を書き込む時間のに\(\,1\,\)分。
方程式解くのに\(\,30\,\)秒。

といったところですか？中学生の頭の回転は速いですからね。

\(\color{black}{\fbox{　4　}}\)はこれだけです。

問題はあと1つです。
目標は30分で見直しまで終わらせる、くらいになっておくと良いですね。

「一般で受験するんだからそれほど実力ない。」
なんてことはいわないで下さい。
今まで問題への取り組み方を知らなかっただけなんだから、今なら裁量で受験できる、といえるように作業してみましょう。
問2から問4までは裁量問題と同じなのです。

⇒　北海道の公立高校入試2018(平成30年度) 数学問題の解説

問1の解説ですが、問2と合わせて\(\,60\,\)点満点中\(\,35\,\)点。
ここで説明した問4までで\(\,52\,\)点です。

⇒　2018年度北海道公立高校入試大問5(裁量問題4)図形問題の解説

問5は線分の長さと相似の証明だけの図形基本問題です。
裁量問題の問4と同じ問題です。