2018年度北海道公立高校入試大問5(裁量問題4)図形問題の解説

2018年（平成30年）度に北海道で行われた公立高校入試大問5(裁量問題4)の解説です。
問5は図形の線分の長さを求める問題と基本的な相似の証明問題です。
裁量問題の問4になりますが通常通りやれば時間はかかりません。

問題は北海道の公式サイトにもあります。

⇒　北海道2018年一般入試数学問題

裁量問題の問4は同じ問題です。

条件が与えられる理由

問1　長さを求める問題です。

合同でもなく三平方の定理でもありません。
相似ですが、単なる定理で終わります。

条件は
　\(\,\mathrm{BD=DC}\,\)　と　\(\,\mathrm{OD=2}\,\)　
だけです。

なぜこの条件が与えられるか考えたことありますか？

簡単な理由です。
　この条件がないと答えが出ないから。

　与えられた条件はすべて使ったか？
見ながら問題に取り組むと数学の成績はガラッと変わりますよ。
特に入試レベルの総合問題になると明らかに変わります。

基本定理を覚えていないというのは単に努力不足ですが、
（『覚え太郎』だけでも見て下さい。覚えていれば入試に不足はありません。）
それでも答えまでが遠い人は、条件を使っていないから解けないのです。

条件を図示してみましょう。
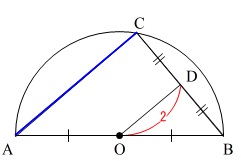ここまで書き込めたら中点連結定理で\(\,1\,\)秒です。
　\(\,\mathrm{AC}=\underline{　4　}\,(\mathrm{cm})\)

『覚え太郎』で確認した方がはやいですが、
（『覚え太郎』-「相似な図形」\(\,\mathrm{Q}65\,\)　）

三角形の\(\,2\,\)辺の中点どうしを結ぶと、
もう一つの辺と平行で半分の長さになります。
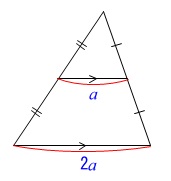教科書にある定理ですよ。
これで\(\,3\,\)点（\(\,60\,\)点満点）です。
普通の配点だと\(\,5\,\)点なので、こういった問題だけ拾っていっても\(\,70\,\)点を切るというのは試験の受け方を間違えているからです。

『超え太郎』は余裕ができてからで良いです。
『覚え太郎』は教科書の範囲なので全部覚えて、試験を受けるときに作業をする。
それだけです。

試験の結果は受けるまでの準備で決まっているのですよ。
　「試験中ひらめいた！」
そんなのありません。

証明は図の中で完結させる

問2は証明です。

与えられた条件を書き込み図の中で完成させるのですが、
公立入試だと気がつくことが1つでもあればほぼつながります。

気がつくことから、次に気がつくこと、がいくつもあるのは大学入試のかなり上位の大学の問題です。

与えられた条件から自分が知っていることを1つでも書き込んでみて下さい。
きっと答えは目の前にあります。

『超え太郎』マスターは気がつくことが多すぎて迷う場合があるでしょうから、
その都度必要な条件を足していって下さい。
高校入試の場合、答えだけ、というのも多いので答え直結のものはズバッと使って良いです。
おそらく試験時間の半分くらいで終わるだろうから見直しは徹底して下さい。

条件を図示します。
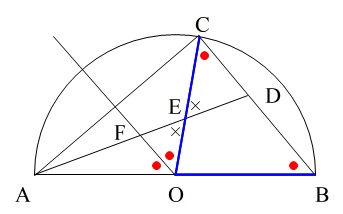終わりです。
他にもいろいろなことが言えます。
例えば直径に対する円周角は\(\,90\,\)度なので、\(\,\mathrm{△ABC}\,\)が直角三角形だということを利用しても証明はできそうです。

しかし、先ず気がついたのが、
　「角の二等分線」
という条件から、弧\(\,\mathrm{AC}\,\)の中心角と円周角の関係です。

　\(\,\mathrm{∠AOC=2∠OBC}\,\)
なので中心角を二等分された角は円周角に等しいので
　\(\,\mathrm{∠AOF=∠FOE=∠OBC}\,\)
ここからはわかること何でも良いですよ。

　円の半径は常に等しいので二等辺三角形の底角は等しい
でも良いです。

　同位角が等しいから\(\,\mathrm{OF}\,\)と\(\,\mathrm{BC}\,\)が平行だから錯角が等しい
でも良いです。

これで対頂角が等しいことと合わせ、「2組の角が等しい」ことが言えるので相似の証明は終わりです。
相似条件は必ず書きましょう。
もちろん結論もです。

証明を書いておきますが、図の中で示せないのに証明が書けるはずありません。
図の中で完成させておくことがポイントです。

ただし、結論まで届かない場合は、
　わかることだけでも証明の一部として解答用紙に書く
ことで部分点がもらえるかもしれません。

北海道も証明には部分点を与えています。
証明が完全にできて\(\,5\,\)点ですが、\(\,4\,\)つのポイントに\(\,1\,\)点ずつくれています。
つまり部分点で\(\,3\,\)点までもらえる可能性はあるわけです。
（部分点\(\,4\,\)つで完成するので\(\,4\,\)点というのは考えにくい。）

証明の書き方ですが、書き慣れていない人向きな方法で進めます。
理由を後書きする方法です。

（証明）
　\(\,△\mathrm{CDE}\,\)　と　\(\,△\mathrm{OFE}\,\)　において

　\(\,∠\mathrm{CED}=∠\mathrm{OEF}　（対頂角は等しい）　･･･①\,\)

　\(\,\mathrm{∠\color{red}{AOC}=2∠ABC=2∠\color{blue}{OBC}}　（円周角の定理）　･･･②\,\)

　\(\,\mathrm{∠AOF=∠FOE}　（仮定）　･･･③\,\)
③より
　\(\,\mathrm{∠\color{red}{AOC}=2∠\color{blue}{AOF}}　･･･④\,\)
②④より
　\(\,\mathrm{∠\color{blue}{OBC}=∠\color{blue}{AOF}}　･･･⑤\,\)
⑤から同位角が等しいので
　\(\mathrm{BC}\)　∥　\(\mathrm{OF}　･･･⑥\)
⑥より
　\(\,\mathrm{∠ECD=∠EOF}　（平行線の錯角は等しい）　･･･⑦\,\)
①⑦より
　2組の角がそれぞれ等しいので
　　\(\,△\mathrm{CDE}\,\)　∽　△\(\,\mathrm{OFE}\,\)　（証明終わり）

①⑤⑥⑦に部分点が与えられます。
ただし、証明もこれだけではないのでこの部分点は信じなくて良いです。

平行⑥は言えなくても、錯角は言えなくても⑦は言えます。

（証明）
　\(\,△\mathrm{CDE}\,\)　と　\(\,△\mathrm{OFE}\,\)　において
対頂角が等しいことより
　\(\,\mathrm{∠CED=∠OEF}　･･･①\,\)
仮定より
　\(\,\mathrm{∠AOF=∠EOF}\,\)
であり、円周角の定理からこれらの角は弧\(\,\mathrm{AC}\,\)の円周角に等しいから
　\(\,\mathrm{∠EOF=∠OBC}　･･･②\,\)
また、円の半径は常に等しいので\(\,\mathrm{△OBC}\,\)は二等辺三角形であり、
底角が等しいことから
　\(\,\mathrm{∠OBC=∠OCB}\,\)
が言えるので、②と合わせて
　\(\,\mathrm{∠ECD=∠EOF}　･･･③\,\)
①③より
　2組の角がそれぞれ等しいので
　　\(\,\mathrm{△CDE}\,\)　∽　\(\,\mathrm{△OFE}\,\)　（終わり）