2018年京都府公立高校入試(前期)数学問題の問2関数の解説

京都府で2018年（平成30年）度に行われた公立高校入試の前期問題の問2の解説です。
問2は関数総合問題ですが基本的でよくある問題です。
面積の問題は具体的に数値を使うか、比を利用するかで大きく方針が変わります。

問題は京都府の公式サイトにもあります。

⇒　京都府2018年公立入試の前期数学問題

比例定数の決定

(1)は\(\,y\,\)が\(\,x^2\,\)に比例する関数の比例定数を決定するおまけ問題です。
比例定数は原点以外の1点があれば求まるので、与えられた点の座標を代入です。

公立高校入試ではこの比例定数問題に点数をくれることが多いです。
必ず拾っておきましょう。

京都府の場合は\(\,\color{red}{50点満点}\,\)なので配点\(\,2\,\)点は\(\,\color{red}{100}\,\)点満点の\(\,\color{red}{4点に相当}\,\)します。

比例定数を出す前に条件を整理しておきましょう。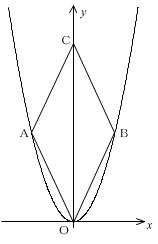

　\(\,\mathrm{A}\,(\,-3,12\,)\,\)
　\(\,\mathrm{C}\,\)は\(\,y\,\)軸上
　\(\,\mathrm{OBCA}\,\)はひし形

ですが、
　\(\,\mathrm{OBCA}\,\)がひし形
であることからすべての頂点の座標が分かります。

　\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)座標が同じ
対称性から
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,-3\,\)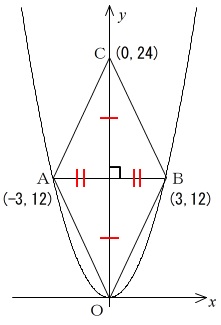

　\(\,\mathrm{C}\,\)の\(\,y\,\)座標は\(\,\mathrm{A}\,\)の\(\,y\,\)座標の\(\,2\,\)倍

これらのことを座標上に示すと右のようになります。

これで(2)までは答えが出ます。

このように座標上に示すと分かり易くなります。

上に書き出した条件を見るのと、座標上に書き込んだ右の図とを比べて、グラフより条件を見ている方が分かり易いという人はそのままで結構です。

ただ、頭の中で考えて解いて行くと、次に続く誘導に乗れなくなりますよ。
目で見て確認できるように座標上に書き出すことが関数攻略の大きなポイントです。

(1)の比例定数を決めましょう。

関数\(\,y=ax^2\,\)は\(\,\mathrm{A(\,\color{red}{-3}\,,\,\color{blue}{12}\,)}\,\)を通るので、
　
　\(\begin{eqnarray}
\color{blue}{12}&=&a\times (\color{red}{-3})^2\\
12&=&9a\\
9a&=&12　（\color{red}{両辺を入れかえただけ}）\\
\displaystyle a&=&\frac{12}{9}=\underline{　\frac{4}{3}　}
\end{eqnarray}\)

\(\,\mathrm{B}\,\)も\(\,y=ax^2\,\)を通るので代入するのは\(\,\mathrm{B}\,\)でも良いですが、
条件を整理しているからできることです。

問題通りに進めれば\(\,\mathrm{A}\,\)を入れる人が9割以上でしょう。

直線の式の求め方

(2)直線は\(\,2\,\)点が分かれば求められます。

直線は\(\,\mathrm{B,C}\,\)を通るので

　\(\begin{eqnarray}
\mathrm{B}\,(\,3&\,,\,&12\,)\\
\mathrm{C}\,(\,0&\,,\,&24\,)
\end{eqnarray}\)

から傾きを先に出します。

　\(\begin{eqnarray}
\color{red}{傾き}&=&\color{magenta}{変化の割合}\\
\displaystyle &=&\color{red}{\frac{　y\,の増加量　}{　x\,の増加量　}}
\end{eqnarray}\)

\(\,x\,\)の増加量は\(\,x\,\)座標の差になりますが、上のように座標を並べて引きます。
このとき\(\,x\,\)成分で下から上を引いたら\(\,y\,\)成分も下から上を引きます。
そうしないと傾きは＋と－が逆になります。

だから、いつも下から上を引くと決めておくと良いです。
何故上から下ではないのか？
理由はありますが、どちらでも良いですよ。
素直な人はおすすめした通り下から上を引いて統一しています。

　\((\,x\,の増加量\,)=(0)-(3)=\color{red}{-3}\,\)
　\((\,y\,の増加量\,)=(24)-(12)=\color{blue}{12}\,\)
なので
　\(\,\displaystyle (傾き)=\frac{\color{blue}{12}}{\color{red}{-3}}=-4\,\)

このことから求める直線の方程式は

　\(\,y=-4x+b\,\)　とおけるので

\(\,\mathrm{B,C}\,\)のどちらかを代入して切片を決めます。
どちらの点を代入しても結果は同じです。
ここでは\(\,\mathrm{C}\,\)を代入しますが、切片は分かっているので代入するまでもありませんね。

　\(\,\mathrm{C\,(\,0\,,\,24\,)}\,\)なので\(\,\color{red}{切片が\,24}\,\)

よって求める直線は

　\(\,\underline{　y=-4x+24　}\,\)

\(\,\mathrm{B}\,\)を代入しても同じ式が出てきます。
というか、同じ式が出てこなければ計算ミスしています。

\(\,y=-4x+b\,\)に\(\,\mathrm{B\,(\,3\,,\,12\,)}\,\)を代入して
　\(\begin{eqnarray}
12&=&-4\times (3)+b\\
12&=&-12+b\\
12+12&=&b\\
24&=&b
\end{eqnarray}\)

同じく　\(\,\underline{　y=-4x+24　}\,\)

面積を利用して座標を求める方法　

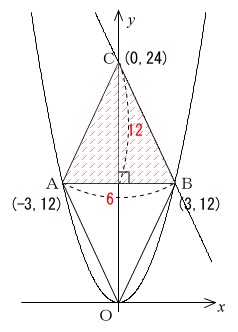\(\,\mathrm{D}\,\)は\(\,\mathrm{BC}\,\)上の点で\(\,x\,\)座標は正という条件はありますが、
\(\,\mathrm{△ABC}\,\)の面積は
　\(\displaystyle \frac{1}{2}\times 6\times 12=36\)

なので\(\,\mathrm{△ADC}\,\)の面積が\(\,12\,\)となるのは、
\(\,\mathrm{D}\,\)が\(\,\mathrm{BC}\,\)の範囲内にあるときだと分かります。
\(\,\mathrm{△ABC}\,\)より面積が小さいからですね。
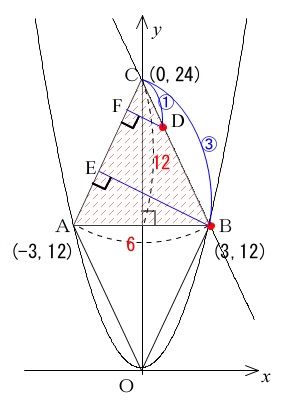\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ADC}\,\)は\(\,\mathrm{AC}\,\)を共通の底辺としていると見れば、
　高さが\(\displaystyle \frac{1}{3}\)のとき

だというのは分かりますが高さを直接比較するのはやっかいです。
しかし、相似を利用すれば簡単です。

　垂線\(\,\mathrm{BE,DF}\,\)を引くと
　\(\,\mathrm{△CBE}\,\)　∽　\(\,\mathrm{△CDF}\,\)
なので
　\(\,\mathrm{DC:BC=1:3}\,\)
となるとき\(\,\mathrm{△ADC}\,\)の面積は\(\,\displaystyle \frac{1}{3}\,\)の\(\,12\,\)になります。

このとき\(\,x\,\)座標も同じ比になるので
　\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,1\,\)
また\(\,\mathrm{D}\,\)は\(\,\mathrm{BC}\,\)上の点なので
　\(\,y=-4\times (1)+24=20\,\)

よって　\(\,\mathrm{D\,\underline{　(\,1\,,\,20\,)　}}\,\)

面積の圧縮が関係するときの高さの比較は相似ですね。
図の中で終わらせてみました。
この程度の問題だと計算はほとんど必要ないです。

\(\,　\large{2}　\,\)はこれで終わりです。

⇒　京都府公立高校入試2018年前期試験の数学問題3の解説

\(\,　\large{3}　\,\)は確率です。

⇒　京都府公立高校入試数学の過去問と解答解説

同様な問題は全国にありますが、
京都府の問題は応用よりも作業量がかなりあります。

過去問に目を通し、どれくらいの分量かは確認しておいた方が良いです。