2018年京都府公立高校入試前期試験の数学問題5の解説

2018年に京都府で行われた公立入試の前期問題問5の解説です。
問5は空間図形です。
空間図形では次元を下げれば平面なので、方針は1つで良いです。
また、この問題は見分けがつきにくいようで実は非常に簡単な問題なのでさっと済ませます。

問題は京都府の公式サイトにもあります。

⇒　2018年京都府公立高校入試前期数学問題

　\(\,\large{5}\,\)　は正四角錐の立体問題です。

空間図形の線分の長さと体積の求め方

まずは問題全体にある条件を抜き出し図示しておきましょう。

　底面は\(\,1\,\)辺\(\,6\,\)の正方形
　他の辺はすべて\(\,\color{red}{6\sqrt{3}}\,\)
　底面の対角線の交点を\(\,\mathrm{H}\,\)
　\(\,\mathrm{OA,OD}\,\)の中点がそれぞれ\(\,\mathrm{P,Q}\,\)
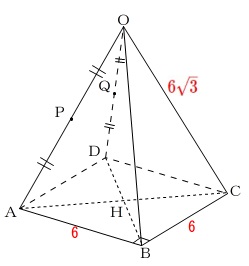錐体の場合はここで書き込みを止めてはダメです。

特に正四角錐なのでもっとたくさんの情報があります。
　\(\,\mathrm{AC⊥BD}\,\)
　\(\,\mathrm{OH⊥AC}\,\)なのでいろいろな長さも分かりますが問題になっているので求めていきましょう。

(1)\(\,\mathrm{AH}\,\)の長さですが、\(\,\mathrm{AH}\,\)を含んだ面を抜き出します。
\(\,\mathrm{△OAC}\,\)でも出ますが、底面の方がはやいでしょう。
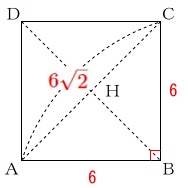\(\,\mathrm{△ABC}\,\)において三平方の定理から（三角定規）
　\(\,\mathrm{AC=6\sqrt{2}}\,\)

なので
　\(\begin{eqnarray}
\mathrm{AH}&=&\frac{1}{2}\times \mathrm{AC}\\
&=&\underline{　3\sqrt{2}　}
\end{eqnarray}\)

今度は\(\,\mathrm{△OAC}\,\)でも\(\,\mathrm{△OAH}\,\)でも良いですが抜き出します。
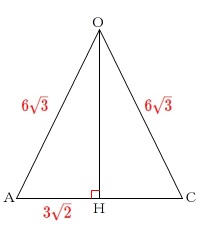直角三角形\(\,\mathrm{OAH}\,\)に三平方の定理を使って、
　\(\begin{eqnarray}
\mathrm{OH^2+AH^2}&=&\mathrm{OA^2}\\
\mathrm{OH^2}&=&\mathrm{OA^2-AH^2}\\
\mathrm{OH^2}&=&(6\sqrt{3})^2-(3\sqrt{2})^2\\
&=&108-18\\
&=&90
\end{eqnarray}\)

\(\,\mathrm{OH>0}\,\)より
　\(\,\mathrm{OH=3\sqrt{10}}\,\)

これは四角錐の高さです。
よって正四角錐\(\,\mathrm{ＯＡＢＣＤ}\,\)の体積は

　\(\hspace{10pt}\displaystyle \frac{1}{3}\times 6\times 6\times 3\sqrt{10}\\
=\underline{　36\sqrt{10}　}\)

錐体の体積が

　\(\color{red}{\displaystyle \frac{1}{3}\times (底面積)\times (高さ) }\)

というのは説明不要でしょう。

部分的な錐体の体積の求め方

(2)は三角錐\(\,\mathrm{OPBQ}\,\)の体積です。

これは底面積を\(\,\mathrm{△OPQ}\,\)と見て高さを求めて、としたいところですが必要ありません。
\(\,\mathrm{OABD}\,\)は\(\,\mathrm{OABCD}\,\)の半分です。

　\(\,\displaystyle \mathrm{OABD}=\color{red}{\frac{1}{2}}\times \mathrm{OABCD}\,\)

さらに\(\,\mathrm{OABD}\,\)を分割します。

中点連結定理から\(\,\mathrm{△OPQ}\,\)は\(\,\mathrm{△OAD}\,\)と相似で
　\(\,\mathrm{AD=2PQ}\,\)

また相似比が\(\,1：2\,\)なので面積比は\(\,1：4\,\)です。

　\(\,\mathrm{△OPQ:△OAD=1:4}\,\)

なので

　\(\,\displaystyle \mathrm{△OPQ=\color{blue}{\frac{1}{4}}\times △OAD}\,\)

\(\,\mathrm{OABD}\,\)と\(\,\mathrm{OPQB}\,\)は高さが同じなので底面積の比が体積比になります。

よって

　\(\begin{eqnarray}
\mathrm{OPBQ}&=&\mathrm{OABCD} \times \color{red}{\frac{1}{2}}\times \color{blue}{\frac{1}{4}}\\
&=&36\sqrt{10}\times \frac{1}{2}\times \frac{1}{4}\\　
&=&\underline{　\frac{9}{2}\sqrt{10}　}
\end{eqnarray}\)

立体の中を通る線分の長さの求め方

(3)はわかりにくいですが、実は簡単です。

\(\,\mathrm{OABCD}\,\)は正四角錐なので\(\,\mathrm{OH}\,\)は面\(\,\mathrm{OAC}\,\)上にあります。
つまり\(\,\mathrm{△OAC}\,\)を抜き出せばいいわけです。

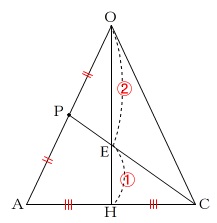2本の中線の交点なので\(\,\mathrm{E}\,\)は\(\,\mathrm{△OAC}\,\)の重心です。

よって
　
　\(\begin{eqnarray}
\mathrm{OE}&=&\frac{2}{3}\times \mathrm{OH}\\
&=&\frac{2}{3}\times 3\sqrt{10}\\
&=&\underline{　2\sqrt{10}　}
\end{eqnarray}\)

簡単に説明しましたがこれで\(\,\large{5}\,\)は終わりです。

いよいよ\(\,\large{6}\,\)です。笑
これがやりたくて京都前期を他の都道府県の問1より先に載せました。

⇒　京都府公立高校入試2018前期問題の数学問6規則性の解説

受験生よってはぶっちゃけ\(\,6\,\)はやらなくて良い捨て問だと思うので、他で確実に点を取っておくと良いです。

⇒　京都府公立高校入試数学の過去問と解答解説

上位校で満点を狙う人は別にして、
普通の受験生は過去問を見て、
基礎は広い範囲で定着させておかなければならないということを知っておきましょう。