京都府公立高校入試2018前期問題の数学問6規則性の解説

京都府で2018年（平成30年）度に行われた公立高校入試の前期問題の数学問6の解説です。
問6は規則性の問題になっていますが規則性を見つけるに苦戦した人が多いかもしれません。
周期を見つければ考えることは少ないけど、とにかく実験がやりにくかった問題です。

何が面白かったかというと、問題はそれほどでもない難易度ではありますが、とにかくスペースがなかった。笑笑

問題は京都府の公式サイトにもあります。

⇒　2018京都府立高校入試前期数学問題

規則性が見えるまで書き出す

規則性の問題では、
　規則性がある程度見えるまで書き出す
と問題の意図が分かるようになります。

そのための誘導がされているのが普通です。

問題のルールですが、\(\,Ⅰ図\,\)と\(\,Ⅱ図\,\)は必要ありません。
ある程度入れ方が理解できたら数字の入った表を見ていきます。

(1)\(\,\color{red}{23},\color{blue}{1},\color{magenta}{2}\,\)の3個が順に入るのは何箱目か？

最初から規則性を考えてもなかなか見つかりません。
\(\,9\,\)箱目までかいてくれているのでとりあえず続きを書き出すといいです。
横にすると画面をはみ出すので縦に並べていきます。

問題用紙にはスペースがありませんのできびしい問題です。
　
\(\begin{array}{|c|c||c|c|c|} \hline
1箱目　 & \,\color{blue}{1}\,&\,\color{magenta}{2}\,&\,3\, & \mathrm{A} \\ \hline
2箱目　 & \,4\,&\,5\,&\,6\, & \mathrm{B} \\ \hline
3箱目　 & \,7\,&\,8\,&\,9\, & \mathrm{C} \\ \hline
4箱目　 & \,10\,&\,11\,&\,12\, & \mathrm{D} \\ \hline
5箱目　 & \,13\,&\,14\,&\,15\, & \mathrm{A} \\ \hline
6箱目　 & \,16\,&\,17\,&\,18\, & \mathrm{B} \\ \hline
7箱目　 & \,19\,&\,20\,&\,21\, & \mathrm{C} \\ \hline
8箱目　 & \,22\,&\,\color{red}{23}\,&\,\color{blue}{1}\, & \mathrm{D} \\ \hline
9箱目　 & \,\color{magenta}{2}\,&\,3\,&\, 4\,& \mathrm{A} \\ \hline
10箱目　 & \,5\,&\,6\,&\,7\, & \mathrm{B} \\ \hline
11箱目　 & \,8\,&\,9\, &\,10\,& \mathrm{C} \\ \hline
12箱目　 & \,11\,&\,12\, &\,13\,& \mathrm{D} \\ \hline
13箱目　 & \,14\,&\,15\, &\,16\,& \mathrm{A} \\ \hline
14箱目　 & \,17\,&\,18\, & \,19\,&\mathrm{B} \\ \hline
15箱目　 &\,20\,&\,21\, & \,22\,& \mathrm{C} \\ \hline
16箱目　 & \,\color{red}{23}\,&\,\color{blue}{1}\, &\,\color{magenta}{2}\,& \mathrm{\color{blue}{D}} \\ \hline
\end{array}\)
出てきました。
　\(\,\underline{　16箱目　}\,\)で\(\,　\underline{\mathrm{D}}\,\)

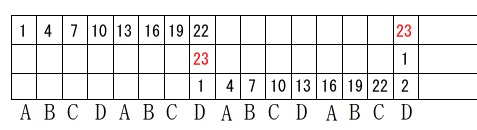
ここである程度気がついてくるかもしれませんが、
着目するのは①ではなく\(\,\color{red}{23}\,\)です。

\(\,23\,\)がくると数字が\(\,1\,\)に戻ります。
つまり、数字の周期は\(\,23\,\)です。

これを続いている通し番号だとすると

\(\,2\,\)回目の\(\,23\,\)は\(\,46\,\)です。
　\(\,46=23\times \color{red}{2}\,\)

\(\,3\,\)回目の\(\,23\,\)は\(\,69\,\)です。
　\(\,69=23\times \color{red}{3}\,\)

この\(\,23\,\)の倍数を並べると

　\(\,23\,,\,46\,,\,69\,,\,92\,,\,115\,,\cdots\,\)

となりますが\(\,3\,\)個ずつ箱に入れていくので

　\(\begin{eqnarray}
23&=&3\times \hspace{4pt}7+\color{red}{2}\\
46&=&3\times 15+\color{blue}{1}\\
69&=&3\times 23+\color{magenta}{0}\\
92&=&3\times 30+\color{red}{2}\\
115&=&3\times 38+\color{blue}{1}\\
138&=&3\times 46+\color{magenta}{0}\\
\cdots&=&\cdots
\end{eqnarray}\)

のように周期ごとにおかれる段数が一つずつずれます。

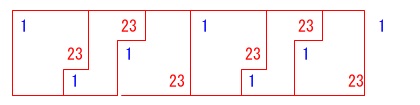
　\(\,1\,\)回目の\(\,23\,\)は\(\,\color{red}{2}\,\)段目
　\(\,2\,\)回目の\(\,23\,\)は\(\,\color{blue}{1}\,\)段目
　\(\,3\,\)回目の\(\,23\,\)は\(\,\color{magenta}{3}\,\)段目
（余りが\(\,\color{magenta}{0}\,\)ということは\(\,3\,\)の倍数で\(\,\color{magenta}{3}\,\)段目）

これくらいの規則性は見ておくと良いですね。

出てきた規則性をまとめておく

気がついた規則性は簡単にでもまとめておくと後で確認しやすいですよ。

　1つの数字は23周期で出現する
　（通し番号を23で割った余りが表示される番号）
　同じ数字は箱の段数が1つずつ変化する

(2)\(\,8\,\)回目の①は何番目の箱か？

\(\,8\,\)回目の①は通し番号でいうと\(\,23\,\)が\(\,7\,\)回出た後の次の数字です。

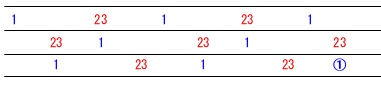
つまり\(\,7\,\)周期が終わった次の①のことで

　\(\hspace{10pt}
23\times 7+1\\
=161+1\\
=162
\)

個目の数字になります。
これを\(\,3\,\)個ずつに区切ると
　
　\(\,162=3\times \color{green}{54}+\color{magenta}{0}\,\)

よって\(\,\underline{　54箱目　}\,\)の\(\,3\,\)段目に入ります。
※
\(\,\color{magenta}{3}\,\)段目に入ることは
　\(\,\color{blue}{1}\,,\,\color{magenta}{0}\,,\,\color{red}{2}\,,\,\color{blue}{1}\,,\,\color{magenta}{0}\,,\,\color{red}{2}\,,\,\color{blue}{1}\,,\,\color{magenta}{0}\,\)
の規則性から分かりますがここでは聞かれていません。笑

箱は\(\color{black}{\fbox{\(\,\mathrm{ＡＢＣＤ}\,\)}}\)の順に\(\,4\,\)箱が組となって並ぶので\(\,54\,\)箱目は

　\(\,54=4\times \color{orange}{13}+2\,\)

\(\color{black}{\fbox{\(\,\mathrm{ＡＢＣＤ}\,\)}}\)の組が\(\,\color{orange}{13}\,\)組終わり、

　\(\color{black}{\fbox{\(\,\mathrm{ＡＢＣＤ}\,\)}\times \color{orange}{13}}\) → \(\mathrm{\color{black}{\fbox{　Ａ　}}}\) → \(\mathrm{\color{black}{\fbox{　Ｂ　}}}\)

次の二箱目の\(\underline{\,\mathrm{Ｂ}\,}\)になります。

ここまでは必死になって書き出せば求まるかもしれません。笑
次はそうも行きません。

複雑な規則性を簡単にする

(3)
ここでも追いかけるのは\(\,23\,\)の倍数です。
\(\,1\,\)でも良いのですが分かり易くするために\(\,23\,\)で考えます。

\(\,23\,\)で周期を持っているので\(\,23\,\)の倍数で終わるところを\(\,1\,\)つの周期とします。

1周期目の\(\,23\,\)は
　\(\,23=3\times 7+\color{red}{2}\,\)
上から2番目で、
箱の種類は箱7つの後の箱で\(\,\color{red}{8}\,\)箱目に入っているので
　\(\,\color{red}{8}=4\times2+0\,\)
4の倍数番目の\(\color{magenta}{\fbox{　Ｄ　}}\)にはいっています。

　このとき2周期目の①は\(\color{magenta}{\fbox{　Ｄ　}}\)の\(\,\color{red}{3}\,\)番目

2周期目の46は
　\(\,46=3\times 15+\color{blue}{1}\,\)
上から1番目で、
箱の種類は箱15個の後の箱で\(\,\color{red}{16}\,\)箱目に入っているので
　\(\,\color{red}{16}=4\times 4+0\,\)
4の倍数番目の\(\color{magenta}{\fbox{　Ｄ　}}\)にはいっています。

　このとき3周期目の①は\(\color{magenta}{\fbox{　Ｄ　}}\)の\(\,\color{red}{2}\,\)番目

3周期目の69は
　\(\,69=3\times 23+\color{magenta}{0}\,\)
上から3番目で、箱の種類は箱\(\,\color{red}{23}\,\)個目の一番下に入っているので
　\(\,\color{red}{23}=4\times 5+3\,\)
4の倍数\(\color{black}{\fbox{\(\,\mathrm{ＡＢＣＤ}\,\)}}\)5組+3番目の\(\color{orange}{\fbox{　Ｃ　}}\)の箱になります。
ここで次の①は\(\color{magenta}{\fbox{　Ｄ　}}\)の箱の\(\,\color{red}{1}\,\)番上になります。
この前の\(\,23\,\)までを\(\,\color{red}{1ブロック}\,\)とします。

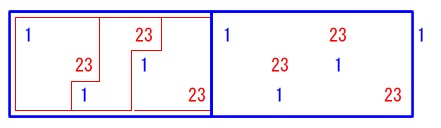
\(\,\color{red}{1ブロック}\,\)に\(\,1\,\)は\(\,3\,\)回出てきますが、
箱の中の位置は1，3，2と移動します。
箱の種類は\(\color{green}{\fbox{　Ａ　}}\),\(\color{magenta}{\fbox{　Ｄ　}}\),\(\color{magenta}{\fbox{　Ｄ　}}\)です。

\(\,2\,\)ブロック目の最後には\(\,23\,\)は\(\color{blue}{\fbox{　Ｂ　}}\)に移動し、
\(\,3\,\)ブロック目の最初の①は\(\color{orange}{\fbox{　Ｃ　}}\)になります。

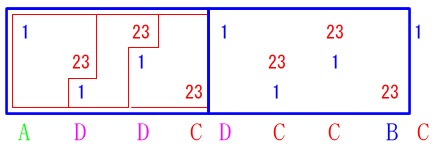
\(\,2\,\)ブロック目の3つの①の箱の中の位置は1,3,2で、
箱の種類は\(\color{magenta}{\fbox{ Ｄ }}\),\(\color{orange}{\fbox{ Ｃ }}\),\(\color{orange}{\fbox{ Ｃ }}\)です。

同じように、
\(\,3\,\)ブロック目の3つの①の箱の中の位置は1,3,2で、
箱の種類は\(\color{orange}{\fbox{ Ｃ }}\),\(\color{blue}{\fbox{ Ｂ }}\),\(\color{blue}{\fbox{ Ｂ }}\)です。

\(\,4\,\)ブロック目の3つの①の箱の中の位置は1,3,2で、
箱の種類は\(\color{blue}{\fbox{ Ｂ }}\),\(\color{green}{\fbox{ Ａ }}\),\(\color{green}{\fbox{ Ａ }}\)です。

この4ブロック目の2回目の①が\(\,\mathrm{\color{green}{A}}\,\)の箱に入る2回目の①です。

ではこの前の\(\,\color{red}{23}\,\)を見てみましょう。

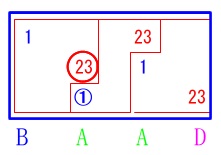
1ブロックに\(\,\color{red}{23}\,\)は\(\,\color{red}{3}\,\)回出てきます。
3ブロックが終わり、
　4ブロック目の1回目の\(\,\color{red}{23}\,\)
が入った後に2回目のAの箱に入る①なので、
\(\,\color{red}{23}\,\)の登場回数は
　\(\,3\times3+1　回\,\)

だから通し番号でいうと2回目のAの箱に入る①は

　\(\hspace{10pt} 23\times (3\times 3+1)+1\\
=23\times 10+1\\
=231\)

1つの箱に3個ずつ入れるので

　\(\,231=3\times 77\)

　\(\underline{　77　箱目　}\,\)

割り切れているので3段目というのも確認できます。

続きを考えると、
第\(\,4\,\)ブロックの\(\,3\,\)回目の\(\,23\,\)は、
　箱の種類は\(\color{magenta}{\fbox{　Ｄ　}}\)
で箱の中の位置は\(\,3\,\)、つまり一番下です。

その次の第\(\,5\,\)ブロックの最初の①は、
　\(\color{green}{\fbox{　Ａ　}}\)の1番上
になるので一番最初と同じ位置に戻りました。

よって4ブロックを1セットとすると、
このセットが繰り返されることになります。

1セットの通し番号を計算しておくと、
　\(\,1周期が23\,\)
　\(\,1ブロックが3周期\,\)
　\(\,1セットが4ブロック\,\)
なので
　\(\,\color{red}{\large{1セット=23\times 3\times 4=276}}\,\)

この1セットの中に\(\color{green}{\fbox{　Ａ　}}\)の①は\(\,\color{red}{3個}\,\)あります。

なので\(\,10\,\)セットあれば\(\color{green}{\fbox{　Ａ　}}\)の①は\(\,30\,\)個入りますが、
\(\,30\,\)個目の\(\color{green}{\fbox{　Ａ　}}\)の①が何箱目かを探さなければなりません。

11セット目の最初の\(\color{green}{\fbox{　Ａ　}}\)の①は31個目の\(\color{green}{\fbox{　Ａ　}}\)の①なのです。

しかし、ここまでくれば簡単です。
逆に戻りましょう。

通し番号でいうと10セット目の最後の23は

　\(\,276\times 10=2760\,\)

これは

　\(\,2760=3\times 920 \,\)

なので\(\,\color{red}{920箱目}\,\)の一番下にあるので

\(\begin{array}{|c|c||c|c|c|} \hline
\color{red}{920箱目}　 & \,21\,&\,22\,&\,\color{red}{23}\, & \mathrm{D} \\ \hline
919箱目　 & \,18\,&\,19\,&\,20\, & \mathrm{C} \\ \hline
918箱目　 & \,15\,&\,16\,&\,17\, & \mathrm{B} \\ \hline
917箱目　 & \,12\,&\,13\,&\,14\, & \mathrm{A} \\ \hline
916箱目　 & \,9\,&\,10\,&\,11\, & \mathrm{D} \\ \hline
915箱目　 & \,6\,&\,7\,&\,8\, & \mathrm{C} \\ \hline
914箱目　 & \,3\,&\,4\,&\,5\, & \mathrm{B} \\ \hline
913箱目　 & \,23\,&\,\color{blue}{\large{①}}\,&\,2\, & \mathrm{A} \\ \hline
\end{array}\)

ありました。

　\(\underline{\,913箱目　\,}\)

いっておきますが、上の表にすべての数字を入れる必要はありませんよ。
一番上の数字か、一番下の数字を\(\,-3\,\)しながら書いていけば良いですよ。

結果、どのような規則性だったかというと、
　\(\,23\,\)と\(\,3\,\)と\(\,4\,\)の最小公倍数\(\,276\,\)
の繰り返しだった、ということです。

\(\,1\,\)～\(\,23\,\)までの数字を\(\,12\,\)回書けば考えることは全く必要無くすべてが見えていたのですが、
時間はいっぱいあっても、そんなスペースはありませんでした。笑

だから、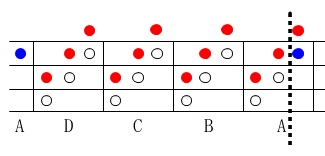という周期表で考えました。