2018年京都府公立高校入試前期試験の数学問題4の解説

2018年に京都府で行われた公立高校入試の前期問題問4の解説です。
問4は平面図形で、相似の証明、線分の長さ、面積計算です。
円の性質と相似が組み合わされていますが、基本的な作業ができていれば簡単に終わります。

問題は京都府の公式サイトにもあります。

⇒　京都府2018年公立入試前期の数学問題

この問題はひねられたところがなく、それほど考えることもないので解説を簡単に済ませておきます。
決してめんどうだからではありません。w

相似の証明方法

図が与えられていて、条件が文章で書いてあるのでややこしく見えますが、
条件を図に書き込むという作業をすればいろいろと見えてきます。

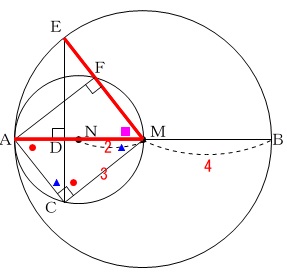
まずは図示するために条件を抜き出してみます。

　\(\,\mathrm{ABは円Mの直径}\,\)
　\(\,\mathrm{AMは円Nの直径}\,\)
　\(\,\mathrm{AB=8}\,\)
　\(\,\mathrm{CM=3}\,\)
　\(\,\mathrm{CE⊥AB}\,\)

図には半径で長さを書き込んでありますが、
　直径\(\,\mathrm{AB=8}\,\)から
　半径\(\,\mathrm{\color{red}{AM}=MB=4}\,\)

　直径\(\,\mathrm{\color{red}{AM}=4}\,\)から
　半径\(\,\mathrm{AN=NM=2}\,\)　
です。

(1)の証明は図の中で済ませてあります。

証明は図の中で済ませておかなければ、
証明を文章で書くことはできません。

よく使う直角三角形の相似の証明です。

（証明）
　\(\,\mathrm{△DCM}\,\)と\(\,\mathrm{△CAM}\,\)において
　\(\,\mathrm{∠\color{red}{MDC}=90°　（仮定 CE⊥AB）}\,\)
　\(\,\mathrm{∠\color{blue}{MCA}=90°　（直径AMの円周角）}\,\)
より
　\(\,\mathrm{∠\color{red}{MDC}=∠\color{blue}{MCA}　･･･①}\,\)
また、
　\(\,\mathrm{∠DMC=∠CMA　（共通）　･･･②}\,\)
①②より
　\(\,\color{red}{2組の角がそれぞれ等しい}\,\)
ので
　\(\,\mathrm{△DCM}\,\)　∽　\(\,\mathrm{△CAM}\,\)
（証明終わり）

これは『超え太郎』にあるので当たり前のこととして利用していると思います。
証明自体もよく出ますが、書くのがめんどくさいくらい簡単ですよね。

合同な三角形の見つけ方と線分の長さの求め方

(2)△FMAと合同な三角形を探します。
図で示したように直角三角形2つの合同です。

　直角三角形\(\,\mathrm{△FMA}\,\)と\(\,\mathrm{△DME}\,\)において
半径は常に等しいから
　\(\,\mathrm{MA=ME}\,\)

また\(\,\mathrm{∠FMA}\,\)と\(\,\mathrm{∠DME}\,\)は共通な角なので
　斜辺と1つの鋭角がそれぞれ等しいので
　\(\,\mathrm{△FMA\,\equiv\,\underline{　△DME　}}\,\)

また\(\,\mathrm{FM}\,\)の長さを求めますが、合同なので
　\(\,\mathrm{FM=DM}\,\)

つまり\(\,\mathrm{DM}\,\)の長さを求めれば良いことになりますが、
(1)で\(\,\mathrm{△DCM}\,\)　∽　\(\,\mathrm{△CAM}\,\)が分かっているので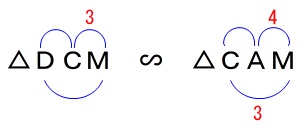比例式から
　\(\begin{eqnarray}
\mathrm{CM:AM}&=&\mathrm{DM:CM}\\
　\hspace{6pt}3\hspace{6pt}:\hspace{6pt}4\hspace{6pt}&=&\mathrm{DM}:\hspace{6pt}3\\
\mathrm{4\times DM}&=&9\\
\mathrm{DM}&=&\underline{　\frac{9}{4}　}
\end{eqnarray}\)

ニコちゃんマークは使えます。笑
もちろん誘導の(1)も使うことになっています。
　

合同な三角形の面積の求め方

(3)は面積です。
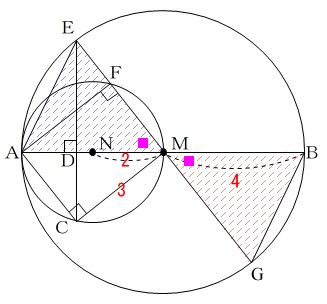\(\,\mathrm{△MGB}\,\)と\(\,\mathrm{△MAE}\,\)は合同なので、
\(\,\mathrm{△MAE}\,\)の面積を求めれば良いということになります。

(2)で\(\,\displaystyle \mathrm{FM=DM=\frac{9}{4}}\,\)と求めているので、
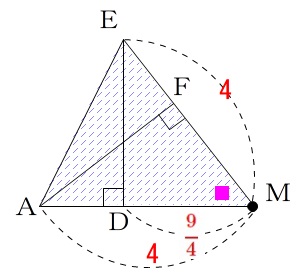半径\(\,\mathrm{ME=4}\,\)と三平方の定理から

　\(\begin{eqnarray}\displaystyle
\mathrm{DE^2+DM^2}&=&\mathrm{ME^2}\\
\mathrm{DE^2}+\left(\frac{9}{4}\right)^2&=&4^2\\
\mathrm{DE^2}&=&4^2-\left(\frac{9}{4}\right)^2\\
&=&16-\frac{81}{16}\\
&=&\frac{256-81}{16}\\
&=&\frac{175}{16}\end{eqnarray}\)

\(\,\mathrm{DE>0}\,\)より（長さだから）
　\(\displaystyle \mathrm{DE}=\frac{5\sqrt{7}}{4}\)
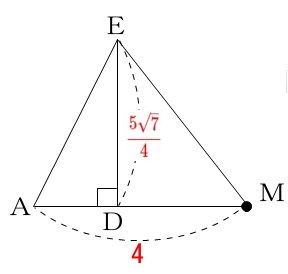よって求める面積は

　\(\begin{eqnarray}\displaystyle
\mathrm{△MGB}&=&\mathrm{△MAE}\\
&=&\frac{1}{2}\times 4\times \frac{5\sqrt{7}}{4}\\
&=&\underline{　\frac{5\sqrt{7}}{2}　}
\end{eqnarray}\)

\(\,175\,\)を素因数分解すると

　\(5\underline{)\hspace{4pt}175}\\
5\underline{)\hspace{10pt}35}\\
\hspace{24pt}7\)

なので\(\,\mathrm{DE^2}\,\)の平方根を求めるところで

　\(\sqrt{175}=5\sqrt{7}\)

は確実にやっておいた方が良いですよ。
せっかくここまでたどり着いても計算ミスするともったいないです。

\(\color{black}{\large{\fbox{　4　}}}\)はここまでです。

⇒　2018年京都府公立高校入試前期試験の数学問題5の解説

問5は立体、空間図形の長さと体積の問題です。

⇒　京都府公立高校入試2018前期問題の数学問6規則性の解説

問6に比べると問5までは普通の問題です。笑

⇒　京都府公立高校入試数学の過去問と解答解説

問5までは例年多少の応用問題を含みますが、
基礎をしっかり定着させておけば対応できます。