2025年度東京都公立高校入試問題【前期】の数学の過去問解説

東京都公立高校入試問題2025年(令和7年)度の数学（前期）の過去問解説です。
例年通りバランス良い出題です。
計算に頼って高得点がとれる問題では無く、
考えることを重視しているので持っている数学の知識をフルに使って問題に取り組むと良いです。

東京都公立高校入試の数学2025年（令和7年）度の問題

都立入試2025年度の前期問題です。

⇒　2025年度都立入試数学前期の問題

分野の偏りは少ないバランスの良い問題構成です。
ある程度の分野分けはされていますが変なクセがある問題では無いので、
総合的に数学の知識を引きだしながら問題に当たると高得点が狙えます。

東京都公立高校入試の数学2025年（令和7年）度の解説

マークシートによる回答は最近増えつつあります。
東京都の過去問でなれておくと良いでしょう。
試験会場でマークシートの記入のしかたを読み取るには時間がかかりますので、
マークのしかたなどはあらかじめ練習しておきましょう。

解説に入りますが、
中途半端な対策となる余計な事は書かずに進めて行く予定です。

第１問小問集合

\(\color{black}{\fbox{１}}\)
作図も含め９問の小問があります。
小問集合では前の問題が解けなくても次の問題は関係ないので、
もし分からなくても気分を入れかえて次の問題に進みましょう。

〔問１〕
　\(\hspace{10pt}3－\color{red}{6^2÷4}\\
=3-\color{red}{9}\\
=\underline{　-6　}\)
計算順序を間違えないようにしましょう。

〔問２〕
　\(\hspace{10pt}\displaystyle \frac{9a-b}{5}-a+2b\\
\displaystyle =\frac{9a-b+5(-a+2b)}{5}\\
\displaystyle =\frac{9a-b-5a+10b}{5}\\
\displaystyle =\underline{\underline{　\frac{4a+9b}{5}　}}\)
通分して分母は１つに、ってわざわざ言う必要はありませんね。

〔問３〕
　\(\hspace{10pt}(3\sqrt{7}+8)(\sqrt{7}-8)\\
=(3\sqrt{7})^2-8^2\\
=63-64\\
=\underline{\underline{　-1　}}\)
展開公式を利用して計算していますが、
ここは地道に展開してでも確実に答えを出しましょう。

〔問４〕方程式を解きます。
　\(\begin{eqnarray}
\frac{9x-6}{2}&=&4x+1\\
9x-6&=&8x+2\\
x&=&\underline{　8　}\
\end{eqnarray}\)
方程式を解くことと、解を求めることは同じです。

〔問５〕連立方程式です。
　\( \begin{cases}
\hspace{4pt} 8x-5y=-3\\
\hspace{4pt} y=\color{red}{2x-1}
\end{cases}\)
代入法で計算しておきます。

　\(\begin{eqnarray}
8x-5(\color{red}{2x-1})&=&-3\\
8x-10x+5&=&-3\\
-2x&=&-8\\
x&=&4
\end{eqnarray}\)
\(\,y\,\)の式に戻して、
　\(\begin{eqnarray}y&=&2(4)-1\\
&=&8-1=7\end{eqnarray}\)

答え\(\underline{　x=4\,,\,y=7　}\)
代入法でも加減法でもどちらでも構いません。

〔問６〕２次方程式を解きます。
　\(\hspace{4pt}x^2-9x+7=0\)

解の公式、覚えておますか？
という問です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{9\pm \sqrt{9^2-28}}{2}\\
&=&\frac{9\pm \sqrt{81-28}}{2}\\
&=&\underline{\underline{　\frac{9\pm \sqrt{53}}{2}　}}
\end{eqnarray}\)
解の公式を覚えていなくても平方完成していけば答えは出ますが、
相当な時間をかけることになるのでやめておきましょう。

〔問７〕関数の変域です。
適当なグラフを描いて考えるのが普通です。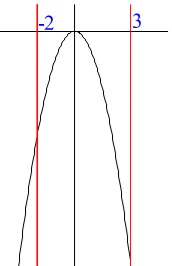
最大値は\(\,x=0\,\)のときの\(\,y=0\,\)、
最小値は\(\,x=3\,\)のときの\(\,y=-9\,\)なので
\(\,y\,\)の変域は\(\,-9≦y≦0\,\)

答え　\(\,\underline{　①　ア　②　オ　}\,\)

〔問８〕確率です。
樹形図で良いですが３枚取り出すのと、２枚残すのは同じことです。
５枚の和が１５なので３枚の和が１０以上となる確率の代わりに、
残った数字の和が５以下となる確率を求めます。
\(\color{black}{\fbox{1}}\)-\(\color{black}{\fbox{2}}\)、\(\color{black}{\fbox{1}}\)-\(\color{black}{\fbox{3}}\)、\(\color{black}{\fbox{1}}\)-\(\color{black}{\fbox{4}}\)、\(\color{red}{\fbox{1}}\)-\(\color{red}{\fbox{5}}\)
\(\color{black}{\fbox{2}}\)-\(\color{black}{\fbox{3}}\)、\(\color{red}{\fbox{2}}\)-\(\color{red}{\fbox{4}}\)、\(\color{red}{\fbox{2}}\)-\(\color{red}{\fbox{5}}\)
\(\color{red}{\fbox{3}}\)-\(\color{red}{\fbox{4}}\)、\(\color{red}{\fbox{3}}\)-\(\color{red}{\fbox{5}}\)
\(\color{red}{\fbox{4}}\)-\(\color{red}{\fbox{5}}\)
２枚残すのは１０通りで和が５以下となるのは４通り。
答え\(\displaystyle \hspace{4pt}\frac{4}{10}=\underline{\underline{　\frac{2}{5}　}}\)

〔問９〕作図なのでさくっと終わらせましょう。
２点から距離が等しい点の集まりは垂直二等分線です。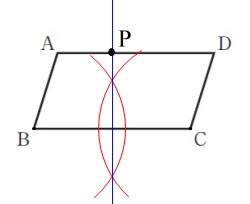頂点\(\,\mathrm{B}\,\)と頂点\(\,\mathrm{C}\,\)から同じ半径の円を書いて、
２つの交点を結べば垂直二等分線のできあがり。
辺\(\,\mathrm{AD}\,\)との交点が点\(\,\mathrm{P}\,\)です。

第２問規則性と文字式

\(\color{black}{\fbox{２}}\)
［先生が示した問題］では具体的な１つの数値が出てくるはずなので、
適当に点を決めて計算すれば答えは出ます。
例えば、１の反対は７です。
　\(\hspace{4pt}a=1\,,\,b=7\)
このとき平均\(\,\mathrm{A}\,\)は４です。
\(\,\mathrm{B}\,\)の値は
　\(\begin{eqnarray}\displaystyle
\mathrm{B}&=&b^2-a^2\\
&=&7^2-1^2\\
&=&48
\end{eqnarray}\)
よって、１２倍となっています。

答え　\(\,\underline{　エ　}\,\)

文字式で計算もできます。
やっておきたい人は確認しておくと良いです。
\(\,aを\,\)決めると\(\,b\,\)は\(\,a\,\)より\(\,6\,\)大きい数なので、
\(\,\hspace{10pt}b=a+6\,\)
平均\(\,\mathrm{A}\,\)は
\(\displaystyle \hspace{4pt}\mathrm{A}=\frac{a+b}{2}=\frac{a+a+6}{2}=a+3\)
一方の\(\,\mathrm{B}\,\)は
\(\displaystyle \hspace{4pt}\mathrm{B}=b^2-a^2=(a+6)^2-a^2=12a+36\)
これから
　\(\displaystyle \frac{\mathrm{B}}{\mathrm{A}}=\frac{12a+36}{a+3}=12\)
問題が求めている方法はこちらかもしれませんが、
次の問題でも同じように文字式があつかえればそれで良いのです。

［\(\,\mathrm{S}\,\)さんのグループが作った問題］
今度は２４等分されているので、
小さい数字を\(\,a\,\)とすると反対の点は\(\,b=a+12\,\)、
もう一つの小さい数字を\(\,c\,\)とすると反対の点は\(\,d=c+12\,\)となります。
このとき、
　\(\begin{eqnarray}
\mathrm{P}&=&\frac{a+b+c+d}{4}\\
&=&\frac{a+a+12+c+c+12}{4}\\
&=&\frac{2a+2c+24}{4}\\
&=&\frac{a+c+12}{2}
\end{eqnarray}\)
これは形を変えておいた方が良いかもしれませんが、
もう一つを処理してから考えましょう。
　\(\begin{eqnarray}
\mathrm{Q}&=&bd-ac\\
&=&(a+12)(c+12)-ac\\
&=&ac+12a+12c+144-ac\\
&=&\color{red}{12(a+c)+144}
\end{eqnarray}\)
ここで\(\,\mathrm{P}\,\)は分数ではやりづらい、と感じるので
　\(\hspace{4pt}2\mathrm{P}=\color{blue}{a+c+12}\)
とすると
　\(\begin{eqnarray}\displaystyle
\mathrm{Q}&=&\color{red}{12(a+c)+144}\\
&=&12(\color{blue}{a+c+12})\\
&=&12\times 2\mathrm{P}\\
&=&24\mathrm{P}
\end{eqnarray}\)
先に\(\,\mathrm{24P}\,\)を文字式で表して、
\(\,\mathrm{Q}\,\)と等しくなる事を言えば良いのか。
\(\hspace{4pt}\displaystyle 24\mathrm{P}=24\times \frac{a+c+12}{2}=12(a+c+12)\)
\(\hspace{4pt}\displaystyle \mathrm{Q}=12(a+c)+144=12(a+c+12)\)
どっちでも良いです。

証明では文字式がしっかり表せていて、
つなぎの日本語を端的にしておけば大丈夫です。

第３問関数

\(\color{black}{\fbox{3}}\)
関数ですが、問３を難しく考えなければ割と早くクリアーできます。
点\(\,\mathrm{A},\mathrm{B}\,\)は定点、直線\(\,\ell\,\)固定された１次関数です。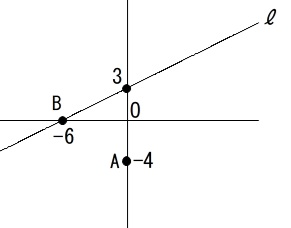
〔問１〕
点\(\,\mathrm{P}\,\)は\(\,\ell\,\)上の点で、\(\,y\,\)座標が\(\,-1\,\)のとき、
　\(\begin{eqnarray}\displaystyle
-1&=&\frac{1}{2}x+3\\
-2&=&x+6\\
x&=&\underline{　-8　}
\end{eqnarray}\)

答え　\(\,\underline{　ア　}\,\)

〔問２〕
直線\(\,m\,\)は点\(\,\mathrm{P}\,\)と点\(\,\mathrm{A}\,\)を通る直線です。
点\(\,\mathrm{P}\,\)が点\(\,\mathrm{B}\,\)に一致するとき、
つまり２点\(\,\mathrm{A\,,\,B}\,\)を通る直線を求めると
点\(\,\mathrm{A}\,(\,0\,,\,-4\,)\,\)
点\(\,\mathrm{B}\,(\,-6\,,\,0\,)\,\)
から
　\(\displaystyle y=-\frac{2}{3}\,x-4\)

答え　\(\,\underline{　ウ　}\,\)

２点を通る直線の求め方
⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い
ここでは答えの１つとして求めていますが、
問題を解く一部になることが多いので短時間で求められるようにしておくと良いです。

〔問３〕文字を設定することで一般的に通用します。
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
点\(\,\mathrm{P}\,\)の座標は\(\displaystyle \,\left(\,t\,,\,\frac{1}{2}\,t+3\,\right)\,\)、
点\(\,\mathrm{Q}\,\)の座標は\((\,t\,,\,0\,)\)とおけます。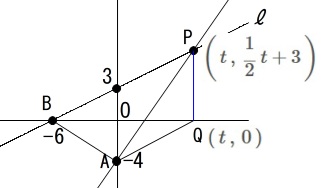問題は\(\,\mathrm{△APB}\,\)の面積が\(\,\mathrm{△AQP}\,\)の２倍のときです。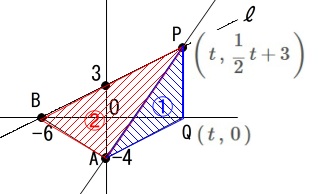ここからは考え方が分かれると思いますが、
普通に
　\(\hspace{4pt}\mathrm{△APB:△AQP}=2:1\)
を利用しましょう。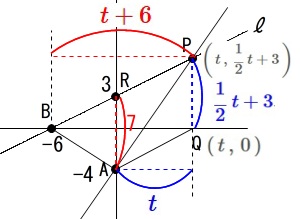\(\,\mathrm{△APB}\,\)は共通の底辺が\(\,\mathrm{AR}\,\)で高さが\(\,\mathrm{B}\,\)と\(\,\mathrm{P}\,\)までの距離とすると、
\(\,\hspace{4pt}\mathrm{△APB=△APR+△ABR}\,\)
から底辺\(\,\color{red}{7}\,\)、高さ\(\,\color{red}{t+6}\,\)、
\(\,\mathrm{△APQ}\,\)は底辺\(\,\displaystyle \color{blue}{\frac{1}{2}\,t+3}\)、高さ\(\,\color{blue}{t}\,\)と見て、
　\(\begin{eqnarray}\displaystyle
\mathrm{△APB}:\mathrm{△APQ}&=&2:1\\
\frac{1}{2}\times 7(t+6):\frac{1}{2}\times \left(\frac{1}{2}\,t+3\,\right)\,t&=&2:1\\
7(t+6):\left(\frac{1}{2}\,t+3\,\right)\,t&=&2:1\\
2\,t\,\left(\frac{1}{2}\,t+3\,\right)&=&7(t+6)\\
t\,(\,t+6\,)&=&7(t+6)\\
(t+6)(t-7)&=&0\\
t&=&-6\,,,\,7
\end{eqnarray}\)
（この比例式の処理は途中省いても良いです。）
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は正の数なので、（問題に条件あり）
\(\hspace{4pt}t=\underline{　7　}\)

または四角形\(\,\mathrm{ABPQ}\,\)の面積が、
\(\,\mathrm{△APQ}\,\)の面積の３倍と見ても底辺と高さは分かりますので、
同じ結果を得られるはずです。
四角形\(\,\mathrm{ABPQ=△PBQ+△ABQ}\,\)として、
底辺\(\,\mathrm{BQ}=t+6\,\)、高さ\(\displaystyle \,\frac{1}{2}\,t+7\,\)
　\(\begin{eqnarray}\displaystyle
(t+6)\left(\frac{1}{2}\,t+7\right):\left(\frac{1}{2}\,t+3\right)\times t&=&3:1\\
3\,t\,\left(\frac{1}{2}\,t+3\right)&=&(t+6)\left(\frac{1}{2}\,t+7\right)\\
3t(t+6)&=&(t+6)(t+14)\\
(2t-14)(t+6)&=&0\\
(t-7)(t+6)&=&0\\
\end{eqnarray}\)

どちらにしても定点と固定されている辺を見つければなんとかなります。
（共通の辺を\(\,\mathrm{AP}\,\)と見ると計算がきついのでは？）

第４問平面図形

\(\color{black}{\fbox{4}}\)
平面図形の問題ですが半円なので円周角などに注目していきましょう。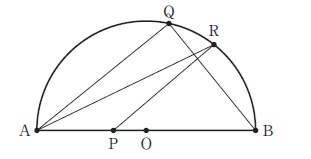

〔問１〕
\(\,\mathrm{AQ=BQ}\,\)なので\(\,\mathrm{△ABQ}\,\)は直角二等辺三角形で底角が\(\,45°\,\)。
\(\,\mathrm{∠QAR}=\color{red}{20^\circ}\,\)から\(\,\mathrm{∠RAB=\color{blue}{25^\circ}}\,\)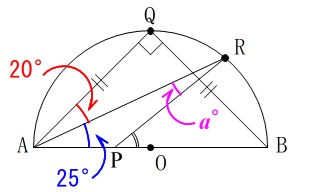
\(\,\mathrm{\color{magenta}{∠ARP}=}\color{magenta}{a^\circ}\,\)のとき
　\(\begin{eqnarray}
\mathrm{∠BPR}&=&\mathrm{∠RAB+∠ARP}\\
&=&\color{blue}{25^\circ}+\color{magenta}{a^\circ}
\end{eqnarray}\)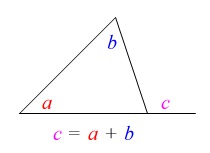
答え　\(\,\underline{　イ　}\,\)
角度の数字だけ見るのでは無く、
自分で図に書き込んで行くことが分かり易くするポイントです。

〔問２〕
図２の条件、
\(\,\mathrm{AP=AQ\,,\,\stackrel{\frown}{\mbox{BR}}=\stackrel{\frown}{\mbox{QR}}}\,\)
から分かることを見ていきます。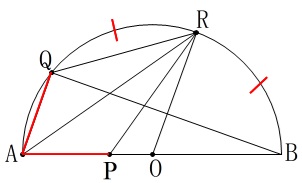\(\,①\,\)で少しヒントをくれているので先にやっておきましょう。

\(\,①\,\)\(\,\mathrm{△APR≡△AQR}\,\)であることの証明です。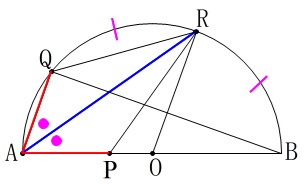
辺\(\,\mathrm{AR}\,\)が共通であること。
同一長の弧に対する円周角が等しいこと。
\(\hspace{4pt}\,\mathrm{∠PAR=∠QAR}\,\)
これと仮定の\(\,\mathrm{AP=AQ}\,\)から、
合同条件「２組の辺とその間の角がそれぞれ等しい。」が言えます。
⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明の書き順は決まっていません。
条件を集めて合同条件さえしっかり書いておけば大丈夫です。

東京都が出してくれている正答表にある、
「『等しい』弧に対する円周角は」
の『等しい』は長さが等しいという意味で使われています。
「同じ弧」、という意味ではありません。

詳しくは説明しませんが、
長さについて等しい場合は「長さが等しい」とは言わなくて良いのです。

\(\,②\,\)
求めるのは\(\,\mathrm{△RST}\,\)の面積が四角形\(\,\mathrm{AORQ}\,\)の何倍か、です。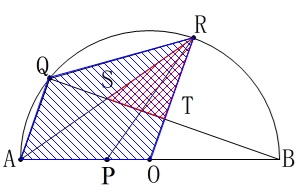条件は\(\,①\,\)に加えて\(\,\mathrm{AP=2OP}\,\)があります。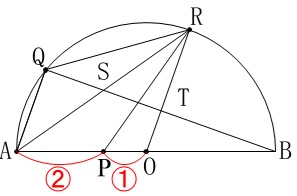ただ、これだけでは到底答えは出てきません。

\(\,①\,\)で証明した合同な三角形に加え、相似な三角形も見つけていきたい。

ということで早速種明かしをすると、
から\(\,\mathrm{△SAQ}\,\)∽\(\,\mathrm{△SRT}\,\)です。
というか合同になるのでその説明をしておきます。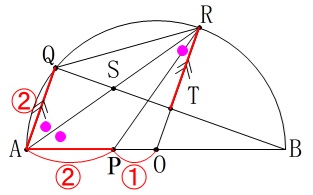半径が等しいことから\(\,\mathrm{△OAR}\,\)は二等辺三角形で、
錯角が等しくなるので相似であり、
中点連結定理と線分比から合同ということまで一気に分かります。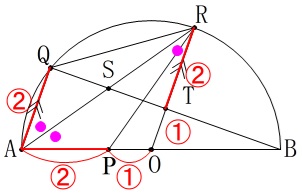\(\,\mathrm{AQ}\,\)∥\(\,\mathrm{OR}\,\)であることは違う方向からも分かります。
１つの弦の垂直二等分線は中心を通ります。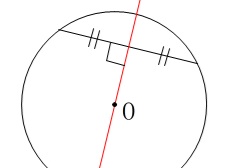直線\(\,\mathrm{RO}\,\)は線分\(\,\mathrm{BQ}\,\)の垂直二等分線なので、
\(\,\mathrm{∠AQB=∠OTB}=90^\circ\,\)と同位角が等しくなるので、
平行であることが分かるということです。
どっちでも良いんです、気がつけば。

さて線分比を書き出しておきましょう。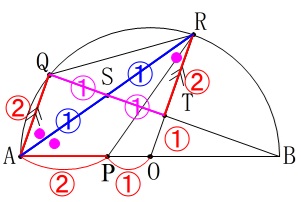ここまでくれば面積比は出てくるでしょう。
\(\hspace{4pt}\mathrm{△APR:△AQR:△OPR}=\color{red}{②}:\color{red}{②}:\color{red}{①}\)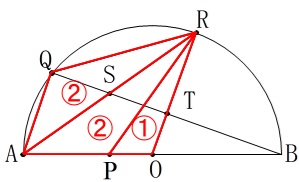ここで\(\,\mathrm{AS=SR}\,\)なので、
\(\,\mathrm{△ASQ}\,\)は\(\,\mathrm{△APR}\,\)の半分です。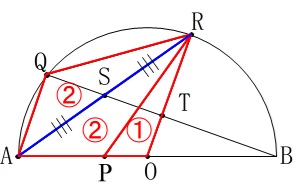\(\,\mathrm{△ASQ}\,\)と\(\,\mathrm{△RST}\,\)は合同で面積が等しいので、
四角形\(\,\mathrm{AORQ}\,\)の面積を\(\,S\,\)とすると
\(\hspace{4pt}\displaystyle \mathrm{△ARQ}=\frac{2}{5}\times S\)
（面積比\(\,\color{red}{②}:\color{red}{②}:\color{red}{①}\,\)だから全体\(\,S\,\)が\(\,\color{red}{⑤}\,\)）
となることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△RST}&=&\mathrm{△ASQ}\\
&=&\frac{1}{2}\times \mathrm{△ARQ}\\
&=&\frac{1}{2}\times \frac{2}{5}\times S\\
&=&\frac{1}{5}\times S
\end{eqnarray}\)

つまり\(\displaystyle \underline{　\frac{1}{5}　} 倍\)。

線分比が出た時点で三角形を置き換えなくても求めることもできます。
（たぶん『覚え太郎』『超え太郎』を使い込んでいる人はこっちでしょう。）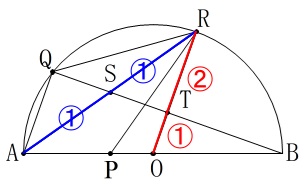
　\(\begin{eqnarray}\displaystyle
\mathrm{△RST}&=&\color{blue}{\frac{1}{2}}\times \color{red}{\frac{2}{3}}\times \mathrm{\color{magenta}{△RAO}}\\
&=&\color{blue}{\frac{1}{2}}\times \color{red}{\frac{2}{3}}\times \color{magenta}{\frac{3}{5}\times S}\\
&=&\frac{1}{5}\times S
\end{eqnarray}\)

線分比を利用した面積の求め方は過去の解説でもたくさんしていると思うので省略します。
カードを持ってる人は覚えているか確認しておきましょう。

第５問空間図形（立体：直方体）

\(\color{black}{\fbox{5}}\)
立体問題です。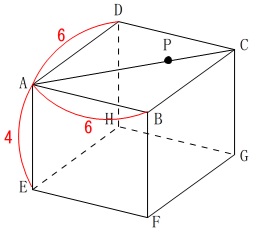直方体ですが長さなどは問題で確認しておきましょう。
〔問１〕
点\(\,\mathrm{P}\,\)が線分\(\,\mathrm{AC}\,\)の中点のとき、
立体\(\,\mathrm{P-AEHD}\,\)は四角錐です。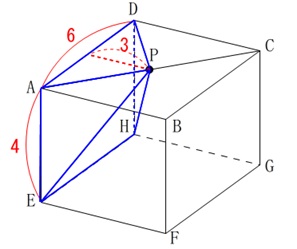底面は長方形で、高さが\(\,\color{red}{3}\,\)なので、
求める体積\(\,V\,\)は、
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 6\times 4\times 3\\
&=&\underline{　24　}\mathrm{cm}^3
\end{eqnarray}\)

錐体の体積の求め方は円錐でも同じです。
⇒　円錐(すい)の表面積や四角錐,五角錐の体積の求め方

〔問２〕
三角形の面積を求めます。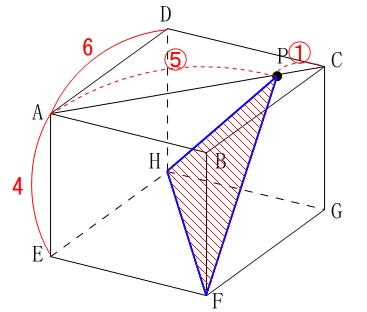
線分\(\,\mathrm{AC}\,\)は正方形の対角線で\(\,6\sqrt{2}\,\)だから
　\(\hspace{4pt}\mathrm{AP}=\color{red}{5\sqrt{2}}\,,\,\mathrm{PC}=\color{red}{\sqrt{2}}\)
線分\(\,\mathrm{HF}\,\)の中点を\(\,\mathrm{M}\,\)、（\(\,\mathrm{EG}\,\)の中点でもある。）
点\(\,\mathrm{P}\,\)から\(\,\mathrm{EG}\,\)に垂線を下ろして交点を\(\,\mathrm{T}\,\)とすると
　\(\hspace{4pt}\mathrm{MT}=\color{blue}{2\sqrt{2}}\)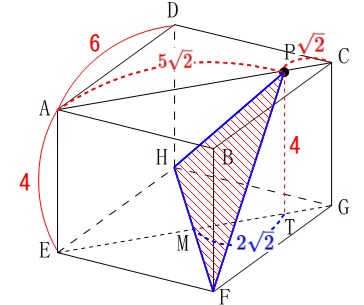\(\,\mathrm{△PHF}\,\)の底辺は\(\,\mathrm{HF}\,\)で
\(\hspace{4pt}\,\mathrm{HF}=6\sqrt{2}\,\)、
高さは\(\,\mathrm{PM}\,\)で三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{PM}^2&=&(\,2\sqrt{2})^2+(\,4\,)^2\\
&=&8+16\\
&=&24
\end{eqnarray}\)
長さなので正の平方根をとって
\(\hspace{4pt}\color{magenta}{\mathrm{PM}}=\color{magenta}{2\sqrt{6}}\)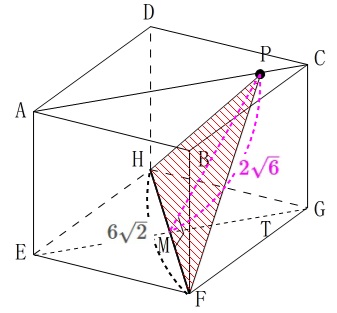求める面積を\(\,S\,\)とすると、
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times \mathrm{HF}\times \mathrm{PM}\\
&=&\frac{1}{2}\times 6\sqrt{2}\times \color{magenta}{2\sqrt{6}}\\
&=&6\sqrt{12}\\
&=&\underline{　12\sqrt{3}　}\mathrm{cm}^2
\end{eqnarray}\)

行程はいくつかありますがきれいな数値です。
立体を部分で見ていく、
という基本通りの作業をしているかを問う問題ですね。
図の中で見ていくと割と早く終わりますよ。

以上です。

一番ややこしく感じたの\(\color{black}{\fbox{4}}\)の〔問２〕でしょうか。
ただ、\(\color{black}{\fbox{1}}\)の〔問１〕も同じ配点だということは覚えておきましょう。
１つの問の配点は大きいので計算はていねいに、
見直しを徹底し確実に得点していきましょう。

⇒　東京都公立高校入試数学の過去問と解答解説

東京都ではマークシートを利用しますが、
ゴリゴリ計算に頼って解く問題ではありません。

じっくり問題を読み取り基本通りの作業を繰り返しましょう。