中学の数学の問題で「曲線の長さを求めよ。」という問題が出てくることがあります。中には学校の先生でも大きな間違いをしている人もいますので注意しておいて下さい。一般的な曲線は「曲がった線」ですが数学では直線も曲線の一部なのです。例題で説明します。
これも前回の記事同様、学校の先生の間違いを指摘したものですが、全ての先生が間違えていると言うことではありませんのでご了承下さい。
ただ、関西の有名大学附属、しかも医学部進学クラス所属の生徒とお母様が「何度提出しても正解になりません。」と泣くほどつらい思いをされた経験です。
「そんなことで」と言わないで下さい。
一生懸命出された宿題に親子で取り組み、何度も何度も見直して、それでも何が違うのか指摘もなく、ただただ「×」とされて返され続けていたのです。
学校の先生に指摘するのはなかなかできないということでしたので、「おそらく先生が求めている答え」、ということで「これを答えにしてみて下さい。」という試みで提出してもらい、「○」をもらってやり過ごした問題でした。
「それでもかまいませんよ。ただ、覚えておいて下さい。」
とお答えしたのですが、非常に残念ではありました。
だからあえてここでその経緯とどう対処したのか、そして本当はどうすべきかを記しておきます。
そのときの問題ではありませんが例題です。
一辺6㎝の正三角形の周りを半径1㎝円がすべらずに1周します。
このとき、円の中心が通過した曲線の長さを求めよ。
中学生の場合、図がついていますので書いておくと
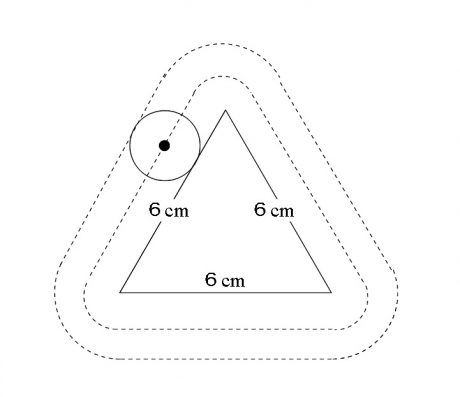
こんな感じです。
求める長さは中心の通過した部分なので正三角形のすぐ外にある点線の長さになります。
この問題の解説は後で詳しくしますので、先に間違えて欲しくないことを書いておきます。
何かというと、タイトルにも書いておいた通り、問題は「曲線の長さを求めよ。」ですがこれには直線部分も含まれるということです。
「曲線って曲がった線のことですよね?」
といいたくなる気持ちもわかります。
「直線ってまっすぐな曲がっていない線のことですよね?」
はい、そうです。
しかし、それは生活する中で使われている言葉です。
数学では「直線は曲線の一部」なのです。
これを間違えないで下さい。
忘れないで下さい。
難しいことをいうつもりはないのですが、ちょっと変わった考え方をしてみましょう。
私たちは地球の表面で生活しています。
これはイメージできるでしょうか?
地面に沿って長い直線を引いたとしましょう。ひたすら長い直線を引いてみて下さい。
例えば海に向かって船は海面と平行に直線的に進みます。
「波に揺られるから直線じゃない。」とかは無しです。
船がダメなら飛行機はいかがです?
地球の表面に沿って同じ高度で飛び続けるっていうのならイメージできますか?
どうなりますか?
まっすぐというわけにもいきませんが地球を1周したすると、直線で進んでいるはずがぐるっと回って元の位置に戻ってきます。
地球は球ですので線で見れば円です。つまりは曲線です。
現実的に見れば直線、でも限りなく大きくすると曲線になります。
しかし、数学では現実的な錯覚も関係なく、直線も曲線に含めるのです。
普段使っている「直線と曲線」は現実的に見分けられる範囲で使っているものだということが少しでもわかって頂けるでしょうか?
この問題に対して、先の生徒はしっかりと直線部分の長さも加えて答えにしていました。
しかし、何度提出しても「×」です。
私も計算ミスはしますので何度も計算して確認しましたし、同じ答えで提出しているにもかかわらずです。
「まさかとは思うのですが、・・・で提出してみて下さい。」
で、ようやく「○」になりました。
普通にあってはならないことだと思うのですが、まして医学部進学クラスの数学担当の先生が、、、ありました。
どうしたかというと、
直線部分の長さを消して提出したのです。
これって特別なことではなく普通の参考書や問題集にも書いている事でしょう。
私の場合、仕事ですから多くの問題集に目を通しているとはいえ、全部の問題集に目を通せているわけではありません。
しかし、この手の問題を取り上げている問題集では曲線部分といえば直線部分も答えにはしっかりと加えてあります。
学校の先生ともなれば生徒に使用させる教材を選ぶ際に、
数多くの問題集には目を通していると思えるのですが、
それ以上にそれを知らずに大学を卒業し学校の先生として数学を教えていることに驚きです。
わかったことがあります。
数学ってそれくらいいい加減に勉強してても学校の先生にはなれる可能性がある。
(全ての先生が知らないということではありませんのでご了承下さい。)
ということと、
受験生はあまり厳密に数学に取り組まなくて良いということです。
ちょっと無責任すぎるので、
数学は厳密なのですが受験数学に限っては厳密である前に、使えることを優先すべき、といいかえておきましょう。
ただ、
この手の問題で曲線を正しく答えていなければ入試では「×」ですよ。
直線部分も含めて答えにして下さい。
さて、問題を解いて解説しておきます。
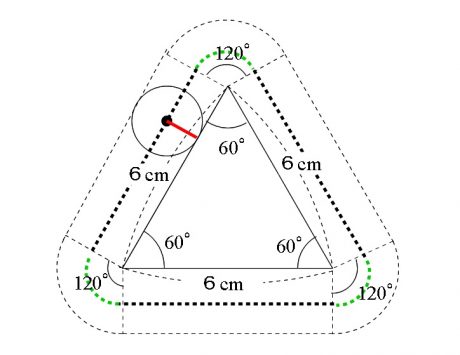
中心が通過するのは、
三角形の各辺と平行に直線的に動く部分と、
頂点で回転する部分の弧の長さとの和になります。
直線部分は各辺に平行で辺の長さと同じになります。
\( \mathrm{6\times 3=18}\)
弧の部分は「半径が1」の円の一部になります。
直径は2となりますが、「中心の通った曲線」なので半径は1です。
さらに、各頂点では120° の回転で、頂点3つなので360°、つまり半径1の円周の長さになります。
これは偶然ではありません。
多角形の周りを回った場合、各頂点で中心が通る弧の中心角の和は360° になります。
多角形の外角の和が常に360°というのは知っているでしょうか?
各頂点での中心の回転は、
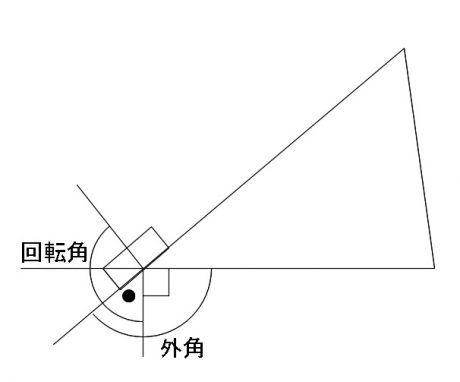
となっています。
中心の頂点での回転角は「90°+●」、外角も「90°+●」で同じです。
これは多角形の1つの外角なので全ての外角を加えれば360°となることはわかりますよね。
偶然ではなく多角形の周りに円を一周させると各頂点での回転角の和は360°ということです。
この各頂点での回転角がわかるかどうかは各辺に垂直な線分が引けるかどうかで差がつきますね。
つまりは図をしっかり書いているかどうかです。
図を書いていない人には解けない問題なのです。
半径1の円周は \(2\pi\) なので答えは「 \(2\pi+18\)(cm)」となります。
もちろんこの問題では、各頂点の角度がわかっていて、1つの頂点での回転角が120°です。
だから各頂点での中心の通る長さは、
\( \displaystyle {2\times \pi\times \frac{120}{360}}\)
これが3頂点あるので、
\( \displaystyle {2\times \pi\times \frac{120}{360}\times3=2\pi}\)
としても良いです。
というか、この問題は中学1年生でも出される問題なので各頂点の回転角を出して求める、というのが普通でしょう。
角度がわかっていれば簡単に出せますからね。
でも、実は角度はわかっていなくても答えは出せるんですよ。
2年生以降で外角の和は360°と知っている場合は入試でも使って構いません。
どちらで解いてもたいして時間がかかるということはありませんが、気がつかなければ少しだけレベルの上がる問題となりますね。
やはり図をしっかり書くということは大切なことです。
円の公式自体を覚えていなければ使えませんよ。
証明できないから。