連立方程式(食塩水の濃度と食塩水を混ぜる文章問題の立式方法と解き方)

食塩水の濃度と食塩水を混ぜる文章問題の立式の方法と解き方の解説です。
食塩水の濃度は理科でもあつかいますが数学では連立方程式の文章問題として出てきます。
濃度の違う２種類の食塩水を混ぜる問題が良く出題されますが、注目するものは濃度ではありません。
ここでは方程式として何を追いかけていくのか見ておきましょう。

食塩水の濃度を求める公式

さて、先ずは濃度の確認からしましょう。理科ですよね。

食塩水の濃度（％）は、

　\(\displaystyle \frac{（\color{red}{食塩}）}{（\color{green}{食塩水}）}\times 100（％）\)

です。
理科の公式では、

　\(\displaystyle \frac{（\color{red}{溶質}）}{（\color{green}{溶液}）}\times 100（％）\)

となっていますが、
　（溶液）＝（溶質）＋（溶媒）
です。

食塩水（溶液）とは、「食塩(溶質)＋水(溶媒)」を意味します。
ここまでは覚えておくようにしましょう。
でないと理科もできないことになります。

一般的に使っている濃度とは「質量パーセント濃度」のことです。
体積など関係なく質量だけの割合ですので難しく考えなくて良いですよ。

濃度の違う食塩水を混ぜるときのポイント

先に問題をあげておきます。

※
問題３（１）はこのページにはありません。

⇒　連立方程式(代金と速さの文章問題の解き方)と線分図の利用

こちらにありますので「問題が飛んでる」などと気にしないでください。

さて、
苦手にしている人が多い食塩水の問題ですが、これは濃度の計算方法を覚えていれば簡単なんです。

ここでもできるだけ図を書いて考えるようにしましょう。
簡単な図でいいんです。

そして、食塩水の問題のコツは\(\,2\,\)つの方程式を立てるときに、
　『「食塩水」と「食塩の量」を追っていく』
です。

方程式は食塩水と食塩で２つ立てる

連立方程式では２つ方程式が必要になってきますがほとんどの問題が、
　①　食塩水の関係式
　②　食塩の関係式
の２つで式を立てます。
（水の関係式はほとんどありません。）

問題に入りましょう。

図を書いて考えるといいんでしたよね。

\(\,4\,\)％の食塩水と\(\,7\,\)％の食塩水を混ぜて、\(\,5\,\)％の食塩水\(\,600\,\)ｇ作ります。
求めたいのは、それぞれの食塩水の量なので、
\(\,4\,\)％の食塩水を　\( x\)　ｇ　,　\(\,7\,\)％の食塩水を　\( y\)　ｇ混ぜるとします。

一つ目の関係式は「食塩水」の量を追えば簡単です。
両方足すと\(\,600\,\)ｇなので、
　\( x+y=600　･･･①\)

二つ目は「食塩」の量を考えます。

\(\,4\,\)％の食塩水とは、
「食塩水」\(\,100\,\)g中に「食塩」が\(\,4\,\)ｇあるということです。

食塩水\(\,1\,\)ｇ中には　\(\displaystyle\frac{4}{100}\)　g　となります。

食塩水　\( x\)　ｇ中だとその　\( x\)　倍の、
　\(\displaystyle \frac{4}{100} \times x\)　(g)　です。

比例計算は時計回りに式をつくる

比例関係になっている数を簡単に出す方法があります。
「比例計算では関係式を時計回りに計算すればいい」、というものです。

例えば、食塩水の中の食塩の量は、食塩水の量が多くなればなるだけその中に含まれる食塩の量も多くなります。

だからこれは比例の関係です。

このとき、
\(\,100\,\)g中に\(\,4\,\)ｇあるなら、\( x\)　ｇ中には？
という関係式は、

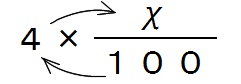
とすればいいのです。

これを知っていると高校の化学なんかは非常に簡単になるのですが、学校ではほぼ確実にに教えてくれません。
（学校の先生が知らないからです。教科書にももちろんありません。）

⇒　比例式の応用 文章題への利用と便利な比の使い方

\(\,7\,\)％の食塩水　\(y\)　ｇ中の食塩も同様に、
　\(\displaystyle 7\times \frac{y}{100}\)
と表せます。

この２つの食塩水を合わせると、\(\,5\,\)％の食塩水\(\,600\,\)ｇになるということから、

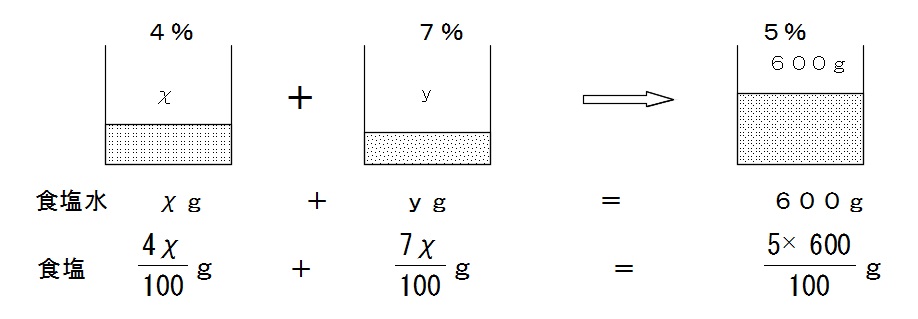
という図が書けます。
自分で書く図はこれだけで十分ですよ。

これがそのまま連立方程式です。
①ももう一度書いておきます。

　\( \begin{cases} x+y=600 \\ \\ \displaystyle \frac{4x}{100}+ \displaystyle \frac{7y}{100}= \displaystyle \frac{5\times 600}{100} \end{cases}\)

２つ目が分数の方程式なので分母を無くす、ですよね。
両辺\(\,100\,\)倍すればいい。

　\( \begin{cases} x+y=600 \\ \\ 4x+7y=3000 \end{cases}\)

これを解くと、
　\( x=400　,　y=200\)　と求まります。

（自分で計算してくださいよ。練習、練習。）

答えは、
　\(\,4\,\)％の食塩水　\(\,400\,\)ｇ
　\(\,7\,\)％の食塩水　\(\,200\,\)ｇ
となります。

連立方程式を解くことは問題ないでしょう。
食塩水と食塩の量を追って２つの方程式が立式できるかどうかが重要です。

連立方程式の解き方は

⇒　加減法とは？連立方程式の解き方とポイント

と

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

で十分に練習しておきましょう。

せっかく立式できても答えが出せないと意味ないですからね。

逆に立式できれば計算はできるでしょう。
連立方程式ほど機械的に解ける問題も少ないですよ。

次は「人数」の増減問題に連立方程式を利用しましょう。

⇒　連立方程式 人数の増減問題は文字でおくのは基準になるもの

人数なので答は整数しかないですよね。
それだけわかれば簡単に解けます。