2018年(平成30年度)に長野県で実施された公立高校入試の数学問題の解説です。
問1、問2の小問集合から問4の平面図形の応用まであります。
答えではなく解き方を答える問題があるので戸惑うかもしれませんが、
8割程度を狙うのであれば気をつけておくのはそこではありません。
問題は長野県でも公開してくれています。
問1.小問集合
問\(\,1\,\)は(1)から(9)まで\(\,12\,\)問ありますが基本問題ばかりですので、ミスの無いように確実に得点しましょう。
式の計算と方程式
(1)
①
\(\hspace{10pt}0-5\\
=\underline{ -5 }\)
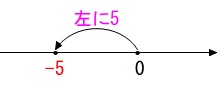
数直線上での移動を考えれば正の数負の数の加減（足し算引き算）は難しくありません。
②
\(\hspace{10pt}(-6^2)\div 12\\
\displaystyle =-36\times \frac{1}{12}\\
=\underline{ -3 }\)
(かっこ)の中の処理が先です。
割り切れないときでも「割り算は逆数のかけ算」ですべて計算できます。
この問題は割り切れるので割り算しても良いですよ。
③
\(\hspace{10pt}\displaystyle \frac{10}{\sqrt{2}}+\sqrt{18}\\
\displaystyle =\frac{10\times\sqrt{2}}{\sqrt{2}\times \sqrt{2}}+3\sqrt{2}\\
\displaystyle =\frac{10\sqrt{2}}{2}+3\sqrt{2}\\
\displaystyle =5\sqrt{2}+3\sqrt{2}\\
=\underline{ 8\sqrt{2} }\)
無理数の分母の有理化と足し算です。
ルートの中身が同じときはルートの前の数で足し算引き算ができます。
文字式と同じようにあつかえば良いだけですね。
ルートの中身を簡単にするときの素因数分解はしっかりやった方がミスは減ります。
\(2\,\underline{)18 }\\
\color{red}{3}\,\underline{)\hspace{4pt}9 }\\
\hspace{14pt}\,\color{red}{3}\)
④
\(\hspace{10pt}\displaystyle 2x-y-\frac{x-y}{5}\\
\displaystyle =\frac{5(2x-y)-(x-y)}{5}\\
\displaystyle =\frac{10x-5y-x+y}{5}\\
\displaystyle =\underline{ \frac{9x-4y}{5} }\)
通分するときは分母を1つにすると、分子の計算に集中できます。
分子には（かっこ）がついていることを忘れずに注意しておきましょう。
(2)
因数分解の手順は決まっていますが、
この問題は展開して整理することからです。
\(\hspace{10pt}(x+5)(x-1)-2x-3\\
=x^2+4x-5-2x-3\\
=x^2+\color{blue}{2}x\color{red}{-8}\)
かけて定数項の\(\color{red}{\fbox{ -8 }}\)になる組み合わせは
\(\color{black}{\fbox{1×8}}\) \(\color{black}{\fbox{2×4}}\)
のどちらかがマイナスになる組み合わせしかありません。
組み合わせで足して\(\,x\,\)の\(\,1\,\)次の項の係数\(\,\color{blue}{+2}\,\)になるのは
\(\color{red}{\fbox{ 4 と -2 }}\)
なので
\(\hspace{10pt}x^2+\color{blue}{2}x\color{red}{-8}\\
=\underline{ (x+4)(x-2) }\)
(3)
方程式は\(\,2\,\)次方程式に限らず左辺にすべての項を集めて、右辺を\(\,0\,\)にすることが基本です。
リンク先で説明していますが、平方根型は例外だと考えておいても良いです。
\(\begin{eqnarray}
3x^2+x&=&1\\
3x^2+x-1&=&0\\
\end{eqnarray}\)
因数分解はできそうもありませんので解の公式を使います。
解の公式は導けなくても良いので、必ず使える様になっておきましょう。
\(ax^2+bx+c=0\)
の解は
\(\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\)
です。
\(\begin{eqnarray}
x&=&\frac{-1\pm\sqrt{1^2-4\times 3\times (-1)}}{2\times 3}\\
&=&\frac{-1\pm\sqrt{1+12}}{6}\\
&=&\underline{ \frac{-1\pm\sqrt{13}}{6} }
\end{eqnarray}\)
正負の数と関数と図形の基本問題
(4)
分かっているのは\(\,2\,\)月\(\,9\,\)日の最低気温です。
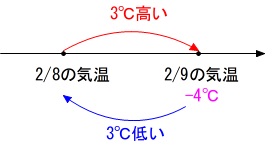
\(\,2\,\)月\(\,8\,\)日の最低気温は
\(-4-(3)\)
となるので一致するのは
（答え） \(\underline{ イ (-4)-3 }\)
(5)
\(\,y\,\)が\(\,x\,\)に反比例するときの関係式は、
\(\displaystyle y=\frac{\color{red}{a}}{x}\) または \(xy=\color{red}{a}\)
となります。
\(\,\color{red}{a}\,\)は「比例定数」です。
反比例でも「比例定数」というのを忘れないようにしましょう。
それぞれを関数にしてみましょう。
ア
三角形の面積の関係なので
\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times x\times y&=&10\\
xy&=&20\\
y&=&\frac{20}{x}
\end{eqnarray}\)
反比例です。
イ
残りのページが\(\,y\,\)なので
\(y=150-x\)
\(\,1\,\)次関数です。
ウ
代金が\(\,y\,\)なので
\(y=120x\)
比例です。
エ
代金が\(\,y\,\)です。
\(\,x\,\)の\(\,3\,\)割は\(\,0.3x=\frac{3}{10}x\,\)なので割引後の代金は
\(\displaystyle y=0.7x=\frac{7}{10}x\)
比例です。
（答え） \(\,\underline{ ア }\,\)
(6)
関数\(\,y=ax^2\,\)の比例定数の大小関係です。
上に凸（下に開いている）放物線の比例定数\(\,c\,\)は負なので一番小さいのは分かります。
下に凸（上に開いている）放物線のときは比例定数が大きいほど\(\,x\,\)の変化に対して、\(\,y\,\)は大きく変化するので、
\(\,a\,＜\,b\,\)
よって
\(\underline{ c\,＜\,a\,＜\,b }\)
比例定数を文字のまま考えるのでは無くて、具体的な数字を入れて見ればすぐに分かります。
(7)
\(ＡＢ\,/\!/\,ＣＤ\,/\!/\,ＥＦ\)
\(\,\mathrm{AB=15}\,\)
\(\,\mathrm{EF=3}\,\)
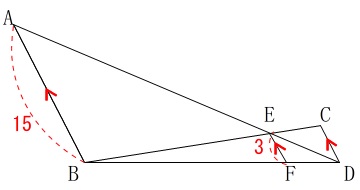
相似ですね。
平行線のときは同位角は等しくなるので、
\(ＡＢ\,/\!/\,ＥＦ\)
だから
\(\,\mathrm{△DAB}\,\) ∽ \(\,\mathrm{△DEF}\,\)
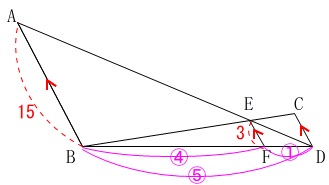相似比は\(\,15:3=\color{magenta}{5:1}\,\)
また \(ＣＤ\,/\!/\,ＥＦ\) なので
\(\,\mathrm{△BEF}\,\) ∽ \(\,\mathrm{△BCD}\,\)
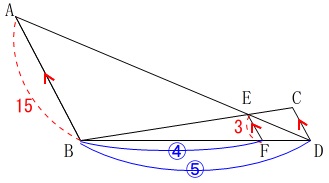相似比は\(\,\color{blue}{4:5}\,\)です。
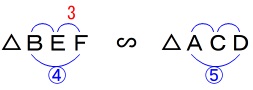よって、
\(\begin{eqnarray}
4:5&=&3:\mathrm{DC}\\
4\times \mathrm{DC}&=&5\times 3\\
\mathrm{DC}&=&\underline{ \frac{15}{4} } (\mathrm{cm})
\end{eqnarray}\)
比例式ではなく、
\(\displaystyle \,\mathrm{DC=\frac{5}{4}\times EF}\,\)
でも良いですけど、相似では比例式を利用した方が確実です。
どちらもやっていることは同じですが、ニコちゃんマークを書くか書かないかは高校に行って差が出ます。
整数の性質と確率の基本
(8)
整数の和の性質です。
答えは無数にあります。
整数の和は、
\(\,(\color{red}{偶数})+(\color{red}{偶数})=(\color{red}{偶数})\,\)
\(\,(\color{red}{偶数})+(\color{blue}{奇数})=(\color{blue}{奇数})\,\)
\(\,(\color{blue}{奇数})+(\color{blue}{奇数})=(\color{red}{偶数})\,\)
の3つの場合があります。
和が偶数になるのは
\(\,(\color{red}{偶数})+(\color{red}{偶数})=(\color{red}{偶数})\,\)
だけでは無く
\(\,(\color{blue}{奇数})+(\color{blue}{奇数})=(\color{red}{偶数})\,\)
の場合があるので、
\(\,\underline{ あ 3 い 5 う 8 }\,\)
などのように\(\color{black}{\fbox{ あ }}\)、\(\color{black}{\fbox{ い }}\)に奇数を選べば和はすべて偶数になります。
これは引き算においても同じことが言えますが、長くなるのでここでは触れないことにします。
(9)
玉を取り出して、元に戻す確率です。
（用語は高校で覚えれば良いですが、『復元抽出』といいます。）
このとき、\(\,1\,\)回目も\(\,3\,\)回目も確率は同じです。
赤玉\(\,2\,\)個と白玉\(\,1\,\)個入っている袋から取り出すので、
赤玉を取り出す確率は\(\,\displaystyle \frac{2}{3}\,\)
白玉を取り出す確率は\(\,\displaystyle \frac{1}{3}\,\)
よって、赤玉を取り出す確率の方が高くなります。
（答え）\(\,\underline{ ア }\,\)
復元抽出の場合、各回での確率はそれまでの取り出し方は関係ないということです。
やっと問\(\,1\,\)が終わった。
ちょっとのんびりやり過ぎですね。笑
答えを出すだけなら\(\,2,3\,\)分あれば終わるでしょう？
これで配点にして\(\,36\,\)点あるんですよ。
よ～く考えて受験して下さいね。
問2.小問集合
(1)から(3)まであります。
(1)はデータの活用問題、(2)は正四角錐の問題、(3)は円の中心作図と中心角の比例問題です。
データの読み取りの基本
(1)表とヒストグラムからデータの読み取りをします。
①
度数が\(\,15\,\)の階級は、
\(\,\underline{ 800\,\mathrm{g}\,以上900\,\mathrm{g}\,未満の階級 }\,\)
ヒストグラムで度数が\(\,15\,\)の階級を答えれば良いだけです。
②
ヒストグラムから\(\,800\,\mathrm{g}\,\)未満の【累積度数】は、
\(\hspace{10pt}5+9+10+9+17\\
=50\)
なので、\(\,77\,\)市町村に対して
\(\hspace{10pt}\displaystyle \frac{50}{77}\times 100\\
≒65 (％)\)
答え \(\,\underline{ ウ }\,\)
※
【累積度数】は\(\,2021\,\)年度から本採用になる新課程で出てくる用語で、
階級の小さい方からその階級までの度数の和を意味します。
③
表に書き込まれている
\(\,合計 \underline{56659}\,\)
という数字は、各市町村の人口がすべて同じ場合の数値です。
例えば、各市町村\(\,1\,\)人ずついると考えれば分かり易いです。
ただ、ゴミの排出量が多い市町村の人口が多い場合は、一人あたりのゴミの排出量は多くなります。
実際にあやさんが計算した数値よりも公表された数値は大きいです。
これは、一人あたりのゴミの排出量が多い市町村の人口の相対度数が大きいことを意味しています。
一人あたりのゴミの排出量を県全体で出したい場合は、
県全体のゴミの総出量を県の総人口で割る
「平均」を出さなければ出ません。
表では各市町村の人口とそれぞれの一人あたりのゴミの排出量が与えられているので、
ゴミの総排出量は、
(各市町村の人口)×(各位市町村の一人あたりのゴミの排出量)の和
なので、その和を長野県の人口で割れば一人あたりのゴミの排出量が出てきます。
この表では途中が切れていますので、実際には計算できません。
ねじれの位置と正四角錐(すい)の側面
(2)
①
辺\(\,\mathrm{AE}\,\)とねじれの位置にある辺をすべて選びます。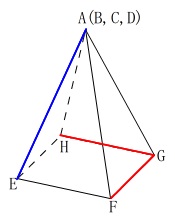
図\(\,3\,\)は組み立てると図\(\,2\,\)の正四角錐になります。
このとき\(\,\mathrm{A,B,C,D}\,\)は頂点で重なります。
ねじれの位置とは同一平面上に無く、
平行でも無い直線のことなので、
答え \(\,\underline{ \mathrm{辺\,GH} }\,\) と \(\,\underline{ \mathrm{辺\,GF} }\,\)
②
側面の三角形の高さを求めます。
条件は正四角錐の高さ\(\,18\,\)
底面の正方形の\(\,1\,\)辺\(\,15\,\)
すぐに三平方の定理が使えますが、
分かり易くするために2つの面を抜き出します。
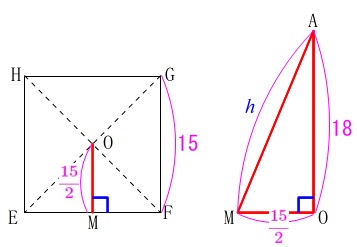底面の正方形\(\,\mathrm{EFGH}\,\)と直角三角形\(\,\mathrm{AOM}\,\)です。
線分\(\,\mathrm{AM}\,\)が求める側面の高さ\(\,h\,\)になります。
\(\,\mathrm{M}\,\)は\(\,\mathrm{EF}\,\)の中点で、\(\,\mathrm{O}\,\)は\(\,\mathrm{EG}\,\)の中点になるので、
中点連結定理から
\(\displaystyle \mathrm{OM}=\frac{1}{2}\mathrm{EG}=\color{magenta}{\frac{15}{2}}\,\)
四角錐の高さ\(\,\mathrm{AO=18}\,\)だから三平方定理から
\(\displaystyle h^2=18^2+\left(\frac{15}{2}\right)^2\)
答え \(\,\underline{ エ }\,\)
円の中心の決定方法と弧の長さの比例関係
北極星を中心に反時計回りにまわるカシオペア座の動きです。
理科の問題でもおかしくないですが、間隔は等しくないので注意が必要です。
①
これはカシオペア座とは関係なく、\(\,3\,\)点を通る円の中心を作図する問題です。
円の中心なのでこの問題では、北極星の位置を探すことになります。
円の中心は2つの弦の垂直二等分線の交点になります。
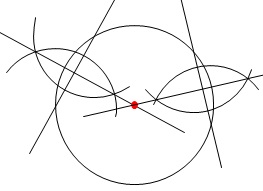この問題では2つの弦がつながっているというで、作図方法は同じです。
線分\(\,\mathrm{AB}\,\)と線分\(\,\mathrm{BC}\,\)を同一円周上の弦とみると、
線分\(\,\mathrm{AB}\,\)の垂直二等分線
と
線分\(\,\mathrm{BC}\,\)の垂直二等分線
の交点を作図するだけです。
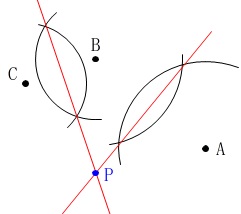
②
もはやカシオペア座と北極星は関係ありません。笑
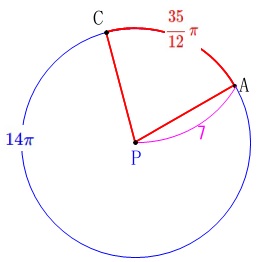
\(\,\mathrm{PA=\color{magenta}{7}}\,\)
\(\displaystyle \mathrm{\stackrel{\large{\frown}}{\mbox{AC}}}=\color{red}{\frac{35}{12}\,\pi}\,\)
このとき\(\,\mathrm{A}\,\)から\(\,\mathrm{C}\,\)まで移動する時間を求めます。
\(\,24\,\)時間で\(\,360°\,\)回転するので周の長さ\(\,\color{blue}{14\pi}\,\)移動します。
\(\,x\,\)時間で\(\,\mathrm{A}\,\)から\(\,\mathrm{C}\,\)まで移動したとすると、
\(\,24\,\)時間で\(\,\color{blue}{14\pi}\,\)移動するとき
\(\,x\,\)時間で\(\displaystyle \color{red}{\frac{35}{12}\,\pi}\,\)移動する
という比例関係が成り立ちます。
\(\begin{eqnarray}
24:\color{blue}{14\pi}&=&x:\color{red}{\frac{35}{12}\pi}\\
14\pi\times x&=&24\times \frac{35}{12}\pi\\
14x&=&2\times 35\\
x&=&\frac{2\times 35}{14}\\
&=&\underline{ 5 } (時間)
\end{eqnarray}\)
比例になれているなら、
\(\displaystyle 24\times \frac{\frac{35}{12}\pi}{14\pi}=x\)
とダイレクトに\(\,x\,\)を求めても良いです。
ただし、この比例関係の表し方は採点者が理解できない可能性がありますので、
\(\displaystyle 14\pi\times \frac{x}{24}=\frac{35}{12}\pi\)
としておいた方が良いですね。笑
問\(\,2\,\)はここまでです。
説明は長いですが、実際に解いて見ると『覚え太郎』会員なら\(\,10\,\)分程度で終わるのではないでしょうか。
配点はここまでで\(\,57\,\)点あります。
この年の受験者平均点を調べてみると分かりますが、基本中心に全体を復習しておけば平均点は取れるでしょう。
⇒ 2018年(平成30年度)長野県公立高校入試数学問題の解説【後半】
問\(\,3\,\)は\(\,1\,\)次関数と応用、問\(\,4\,\)は円2つの交点問題です。
基本が無い状態で応用問題を数多く解いてもムダですよ。
基本をしっかり身につけておけば\(\,7\,\)割や\(\,8\,\)割取ることはそれほど難しいことではありませんよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
