2018年(平成30年度)長野県公立高校入試数学問題の解説【後半】

2018年(平成30年度)に長野県で実施された公立高校入試の数学問題後半の解説です。
問3の1次関数の応用と方程式、問4の2つの円の位置関係と平面図形の応用まであります。
数値はきれいな問題にしてくれていて、計算力はそれほど必要ありませんので考え方をしっかり身につけておけば高得点が狙えます。

問題は長野県でも公開してくれています。

⇒　2018年長野県公立高校入試数学問題

問3.1次関数の応用

\(\,Ⅰ\,\)の加熱と水温上昇の関係と、\(\,Ⅱ\,\)のエレベータの上下と地上からの高さの関係が関数になっています。

いずれにしても何が\(\,x\,\)で、何が\(\,y\,\)としているのかは意識しておきましょう。

1次関数の基本性質と利用

\(\,Ⅰ\,\)
加熱時間を\(\,x\,\)、水温を\(\,y\,\)とすると、
表\(\,1\,\)のように変化したようです。

(1)
(表\(\,1\,\))
　\(\begin{array}{|c|c|c|c|c|} \hline
x & 0 & 1 & 2 & 3 & 4 & 5\\ \hline
y & 18.0 & 21.8 & 26.1 & 29.7 & 34.2 & 38.0\\ \hline
\end{array}\)

この\(\,x,y\,\)を座標上に示すと
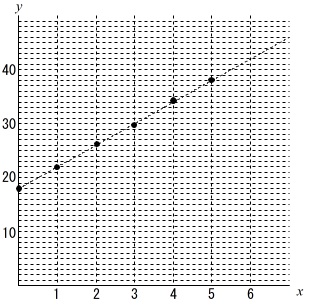わずかにズレはありますが、「ほぼ\(\,1\,\)つの直線上に並んでいる」ように見えます。

こういった実測値で直線を決める場合は、余程ズレが無ければ離れた\(\,2\,\)点を取って方程式を決めるとズレは減ります。

ここでは両端のきれいな数値で出ている座標　
　\(\,(\,0\,,\,18\,)\,\)
　\(\,(\,5\,,\,38\,)\,\)
を通るものとして直線を決定しています。

　\(\begin{eqnarray}\displaystyle
(傾き)&=&\frac{　(y\,の増加量)　}{　(x\,の増加量)　}\\
&=&\frac{　38-18　}{　5-0　}\\
&=&4
\end{eqnarray}\)

なので求める直線の式は\(\,(\,0\,,\,18\,)\,\)(切片)を通るので、

　\(\underline{　y=4x+18　}\)

答え　\(\color{black}{\fbox{あ}}\)　\(\,\underline{　一直線　}\,\)　\(\color{black}{\fbox{い}}\)　\(\,\underline{　y=4x+18　}\,\)

(2)
加熱し続けて温度が上昇しても関数は変わらないとして、
水温が\(\,80℃\,\)になるまでの時間を求めます。

　加熱時間は\(\,x\,\)
　水温は\(\,y\,\)

で表れています。

つまり、\(\,80℃\,\)になるまでの時間が知りたければ、

\(\color{red}{\fbox{\(\,\color{red}{い}\,\)}}\)の

　\(\,\color{red}{y=4x+18}\,\)

において\(\,\color{red}{y=80}\,\)を代入したときの\(\,\color{red}{x}\,\)を求めれば良い。

実際の時間は求めなくて良い問題ですが、

　\(\begin{eqnarray}
80&=&4x+18\\
4x&=&80-18\\
x&=&\frac{62}{4}\\
&=&\frac{31}{2}　(分)
\end{eqnarray}\)

\(\,x,y\,\)が何を表しているか意識しておくだけですね。

1次関数と方程式の利用

\(\,1\,\)階から\(\,27\,\mathrm{m}\,\)の高さにある\(\,10\,\)階まで動くエレベーターの動きを\(\,1\,\)次関数と見ます。

　動き始めてからの時間を\(\,x\,\)
　高さを\(\,y\,\)

とします。

エレベーターの動きは上りと下りは同じ速さとして、

　\(\,36\,\)秒で\(\,27\,\mathrm{m}\,\)

を上下します。

このことから平均したエレベーターの速さは

　\(27\div 36=0.75　(\mathrm{m}/秒)\)

と見ているので、

　上り　\(y=0.75x\)

　下り　\(y=-0.75x+27\)

という関係式で表されることになります。

※
実際には最初の数秒は加速しているので速さは変化しているはずですが、ここでは平均した速さの関数と見なしています。

(1)
速さが毎秒\(\,0.75\,\mathrm{m}\,\)とした理由を示します。

　\(\underline{　27　}\div 36=0.75　(\mathrm{m}/秒)\)

\(\color{black}{\fbox{う}}\)に入る数値は　\(\,\underline{　27　}\,\)

(2)
　\(\,x\,\)の範囲（定義域）が\(\,0\,≦\,x\,≦\,36\,\)のときの
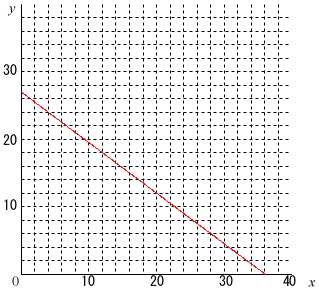
　\(\,y=-0.75x+27\,\)のグラフを書きます。

傾きが\(\,-0.75\,\)で切片が\(\,27\,\)の直線です。

(3)
エレベータは途中の階には止まらないので、
\(\,1\,\)階から\(\,10\,\)階だけの移動を考えれば良いです。

つまり、高さ\(\,0\,\mathrm{m}\,\)と\(\,27\,\mathrm{m}\,\)を往復するだけの動きです。
ただし、\(\,1\,\)階と\(\,10\,\)階では停止時間があるので注意しておきましょう。

①
動き出してから\(\,10\,\)秒後の\(\,\mathrm{A,B}\,\)の高さの差を求めます。

\(\,0\,≦\,x\,≦\,36\,\)において

\(\,\mathrm{A}\,\)は\(\,y=0.75x\,\)なので

　\(\begin{eqnarray}
y&=&0.75\times 10\\
&=&\color{red}{7.5}
\end{eqnarray}\)

\(\,\mathrm{B}\,\)は\(\,y=-0.75x+18\,\)なので

　\(\begin{eqnarray}
y&=&-0.75\times 10+27\\
&=&-7.5+27\\
&=&\color{blue}{19.5}
\end{eqnarray}\)

よって高さの差は

　\(\color{blue}{19.5}-\color{red}{7.5}=\underline{　12　}　(\mathrm{m})\)

この\(\,12\,\mathrm{m}\,\)は\(\,\mathrm{B}\,\)の高さから\(\,\mathrm{A}\,\)の高さを引いた数値です。

\(\,\mathrm{A}\,\)の高さから\(\,\mathrm{B}\,\)の高さを引いた場合、
　\(\,7.5-19.5=\underline{　-12　}　(\mathrm{m})\,\)
となりますが、これも高さの差なので答えですがどちらかを答えにすれば良いですよ。

②
最初に\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の高さが等しくなるのは、
\(\,y\,\)が同じ値になるときなので、

　\( \begin{cases}
\hspace{7pt} y=0.75x　･･･①\\ \\
\hspace{7pt} y=-0.75x+27　･･･②
\end{cases}\)

が成り立つときです。

または、高さの差が\(\,0\,\)であることから

　\(0.75x-(-0.75x+27)=0　･･･③\)

が成り立つときですが、連立方程式と同じことです。

何秒後かを求めるだけなので\(\,x\,\)だけ求めれば良いです。

　\(\begin{eqnarray}
0.75x&=&-0.75x+27\\
75x+75x&=&2700\\
150x&=&2700\\
x&=&\frac{2700}{150}\\
&=&\underline{　18　}　(秒後)
\end{eqnarray}\)

③
\(\,\mathrm{A}\,\)は一度\(\,10\,\)階まで上がり、
\(\,10\,\)階で\(\,\color{blue}{6}\,\)秒間止まり、
\(\,10\,\)階から\(\,1\,\)階に下りています。

\(\,\mathrm{B}\,\)は一度\(\,1\,\)階まで下り、
\(\,1\,\)階で\(\,\color{red}{10}\,\)秒間止まり、
\(\,1\,\)階から\(\,10\,\)階まで上がっています。

\(\,\mathrm{A,B}\,\)ともに\(\,1\,\)回の移動で\(\,36\,\)秒かかるので、

　\(\,\mathrm{A}\,\)は\(\,36+\color{blue}{6}=42\,\)秒後に\(\,10\,\)階を降り始めます。
　\(\,\mathrm{B}\,\)は\(\,36+\color{red}{10}=46\,\)秒後に\(\,1\,\)階から上り始めます。

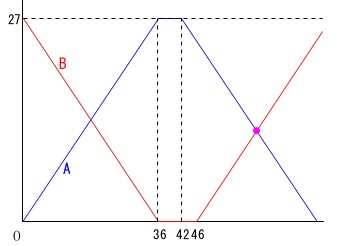この2つの直線の交点を求めれば良いのですが、
関数として連立方程式を解きます。

ただし、\(\,42\,≦\,x\,≦\,78\,\)における交点になります。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

\(\,1\,\)次関数の求め方に自信がない人、時間がかかる人はしっかり復習しておきましょう。

\(\,\mathrm{A}\,\)は
　\(\,(\,42\,,\,27\,)\,\)
　\(\,(\,78\,,\hspace{4pt}0\,)\,\)
を通るので

　\(\displaystyle y=-\frac{3}{4}x+\frac{117}{2}　･･･④\)

同じように\(\,\mathrm{B}\,\)は
　\(\,(\,46\,,\hspace{4pt}0\,)\,\)
　\(\,(\,82\,,\,27\,)\,\)
を通るので

　\(\displaystyle y=\frac{3}{4}x-\frac{69}{2}　･･･⑤\)

交点の座標は④⑤を連立すれば出てきますが、
動き始めてからの時間だけ分かれば良いので、
④⑤の右辺から

　\(\begin{eqnarray}
-\frac{3}{4}x+\frac{117}{2}&=&\frac{3}{4}x-\frac{69}{2}\\
-3x+234&=&3x-138\\
-3x-3x&=&-138-234\\
-6x&=&-372\\
x&=&\frac{372}{6}\\
&=&\underline{　62　}　(秒後)
\end{eqnarray}\)

もちろん\(\,y\,\)を求めればどの高さですれ違うかも分かりますが聞かれていません。

問4.平面図形の応用

図\(\,1\,\)の条件です。

　中心が\(\,\mathrm{O}\,\)の円\(\,\mathrm{O}\,\)の半径は\(\,2\,\)
　外部の点\(\,\mathrm{A}\,\)があり、線分\(\,\mathrm{OA}\,\)と円\(\,\mathrm{O}\,\)との交点を\(\,\mathrm{B}\,\)
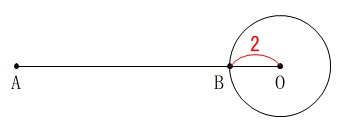図\(\,1\,\)を元に図\(\,2\,\)を書く手順は

　①線分\(\,\mathrm{AB}\,\)上に\(\,\mathrm{B}\,\)以外の点\(\,\mathrm{P}\,\)をとる。
　②線分\(\,\mathrm{PO}\,\)の中点\(\,\mathrm{M}\,\)を中心とする円\(\,\mathrm{M}\,\)を書く。
　③円\(\,\mathrm{M}\,\)と円\(\,\mathrm{O}\,\)の交点をそれぞれ\(\,\mathrm{C,D}\,\)とする。
　④点\(\,\mathrm{O}\,\)と\(\,\mathrm{C,D}\,\)、点\(\,\mathrm{C}\,\)と点\(\,\mathrm{P}\,\)、点\(\,\mathrm{D}\,\)と点\(\,\mathrm{P}\,\)を結ぶ。
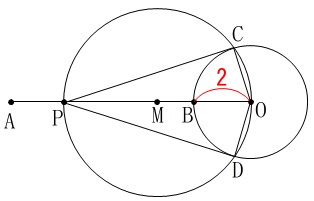言えることはたくさんありますが、問題に合わせて書き込んで行きましょう。

2つの円の交点と合同の証明

\(\,Ⅰ\,\)
\(\,\mathrm{PC=PD}\,\)を証明します。

線分の長さが等しいことは合同をよく使いますが、ここでは合同な三角形を先に見つけます。

合同な三角形を見つけるには図の中に条件を書き込み合同であることを見つけます。
つまり証明を図の中で済ませておくということです。

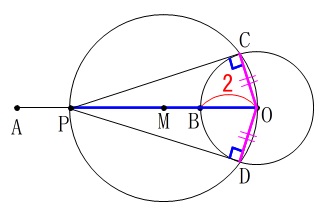
(1)
\(\,\mathrm{△POC}\,\)と合同な三角形は見た目にも明らかです。

（答え）　\(\,\underline{　\mathrm{△POD}　}\,\)

(2)
\(\,\mathrm{PC=PD}\,\)を示すのに合同を証明しますが、図の中で終わっています。

(証明)
　\(\,\mathrm{△POC}\,\)と\(\,\mathrm{△POD}\,\)のおいて

　\(\,\mathrm{PO=PO}\,\)　（共通）　･･･①
　\(\,\mathrm{OC=OD}\,\)　（同一円の半径)　･･･②
また円\(\,\mathrm{M}\,\)の直径に対する円周角なので
　\(\,\mathrm{∠ACO=∠ADO=90^{\circ}}\,\)　･･･③
①②③より
　直角三角形の斜辺と他の1辺がそれぞれ等しい
ので
　\(\,\mathrm{△POC}\,\)　≡　\(\,\mathrm{△POD}\,\)

合同な三角形の相対する辺は等しいので

　\(\,\mathrm{PC=PD}\,\)
（終わり）

半径と辺で作る角度と面積

\(\,Ⅱ\,\)
図\(\,2\,\)の点\(\,\mathrm{P}\,\)が移動します。

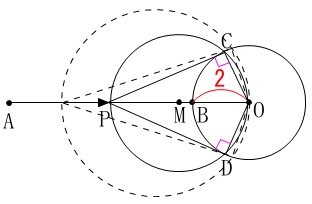
図を書く手順は同じなので当然ですが、中心\(\,\mathrm{M}\,\)も移動します。

だいたいの図形の変化が分かれば、問題に入りましょう。
何も分からないまま問題に入っても時間が無駄になるだけですよ。

(1)
点\(\,\mathrm{M}\,\)と点\(\,\mathrm{B}\,\)が一致するまで動きます。
そのときの様子を図\(\,4\,\)に示します。
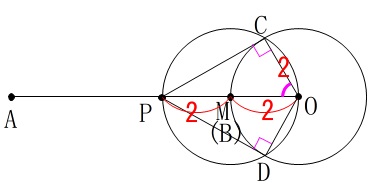\(\,\mathrm{△PCO}\,\)は直角三角形で三角定規なので、

　\(\begin{eqnarray}
\mathrm{OC:PC}&=&1:\sqrt{3}\\
2:\mathrm{PC}&=&1:\sqrt{3}\\
\mathrm{PC}&=&\underline{　2\sqrt{3}　}　(\mathrm{cm})
\end{eqnarray}\)

三角定規の比を覚えていない場合は三平方の定理でも良いですよ。

　\(\begin{eqnarray}
\mathrm{OC^2+PC^2}&=&\mathrm{OP^2}\\
2^2+\mathrm{PC^2}&=&4^2\\
\mathrm{PC^2}&=&16-4\\
&=&12\\
\mathrm{PC}&=&\underline{　2\sqrt{3}　}　(\,\mathrm{PC}\,＞\,0\,)
\end{eqnarray}\)

(2)
さらに\(\,\mathrm{P}\,\)が\(\,\mathrm{O}\,\)に近づいて、\(\,\mathrm{C,M,D}\,\)が\(\,1\,\)直線上に並びます。
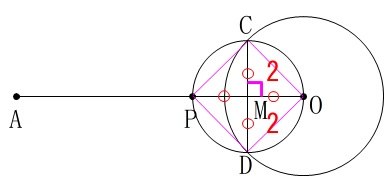このとき、四角形\(\,\mathrm{OCPD}\,\)は正方形になります。

①
\(\,\mathrm{△CPO}\,\)は直角二等辺三角形なので、

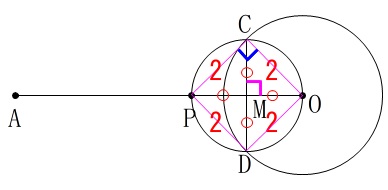
　\(\mathrm{∠CPO=\underline{　45^{\circ}　}}\)

②
正方形\(\,\mathrm{OCPD}\,\)の面積は\(\,1\,\)辺が半径\(\,\mathrm{OC}\,\)の\(\,\color{red}{2}\,\)なので

　\(\color{red}{2}\times \color{red}{2}=\underline{　4　}　(\mathrm{cm^2})\)

(3)
(2)のときよりさらに\(\,\mathrm{P}\,\)が\(\,\mathrm{O}\,\)に近づいて、
円\(\,\mathrm{M}\,\)の面積が円\(\,\mathrm{O}\,\)の面積の\(\,\displaystyle \frac{1}{3}\,\)になるとき、
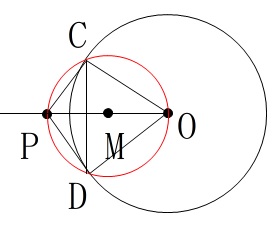\(\,\mathrm{△OCD}\,\)の面積を求めます。

相似な図形では、

　相似比が\(\,\color{red}{a}:\color{blue}{b}\,\)
のとき
　面積比は\(\,\color{red}{a^2}:\color{blue}{b^2}\,\)
です。

円はすべて相似なので、

　面積比が\(\,1:3\,\)
なら、
　半径の比は\(\,\sqrt{1}:\sqrt{3}=1:\sqrt{3}\,\)

円\(\,\mathrm{M}\,\)の面積が円\(\,\mathrm{O}\,\)の面積の\(\displaystyle \,\frac{1}{3}\,\)になるとき、
円\(\,\mathrm{O}\,\)の半径は\(\,\color{red}{2}\,\)なので円\(\,\mathrm{M}\,\)の半径\(\,\color{magenta}{r}\,\)は

　\(\begin{eqnarray}\displaystyle
1:\sqrt{3}&=&\color{magenta}{r}:\color{red}{2}\\
\sqrt{3}\,\color{magenta}{r}&=&2\\
\color{magenta}{r}&=&\frac{2}{\sqrt{3}}\\
&=&\color{magenta}{\frac{2\sqrt{3}}{3}}
\end{eqnarray}\)
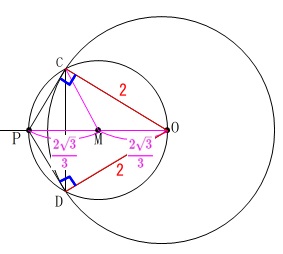\(\,\mathrm{△OCP}\,\)は直角三角形で、\(\,\mathrm{△ODP}\,\)は\(\,\mathrm{△OCP}\,\)と合同です。

円\(\,\mathrm{M}\,\)の直径\(\,\mathrm{OP}\,\)は

　\(\begin{eqnarray}
\mathrm{OP}&=&2\times \mathrm{OM}\\
&=&2\times \left(\color{magenta}{\frac{2\sqrt{3}}{3}}\right)\\
&=&\color{blue}{\frac{4\sqrt{3}}{3}}
\end{eqnarray}\)

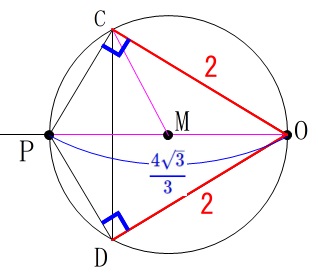
なので、三平方の定理から

　\(\begin{eqnarray}
\mathrm{OC^2+CP^2}&=&\mathrm{OP^2}\\
\color{red}{2}^2+\mathrm{CP}^2&=&\left(\color{blue}{\frac{4\sqrt{3}}{3}}\right)^2\\
4+\mathrm{CP}^2&=&\frac{16}{3}\\
\mathrm{CP}^2&=&\frac{16}{3}-4\\
&=&\frac{16-12}{3}\\
&=&\frac{4}{3}
\end{eqnarray}\)

\(\,\mathrm{CP}\,\)は長さなので\(\,\mathrm{CP}\,＞\,0\)だから

　\(\begin{eqnarray}
\mathrm{CP}&=&\frac{2}{\sqrt{3}}\\
&=&\color{magenta}{\frac{2\sqrt{3}}{3}}　
\end{eqnarray}\)

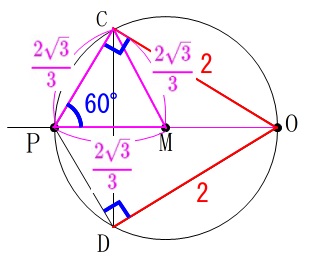このとき\(\,\mathrm{∠COP=30^{\circ}}\,\)なので、
\(\,\mathrm{△OCD}\,\)は正三角形だと分かります。
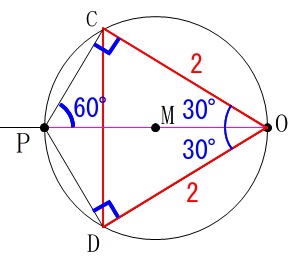つまり\(\,\mathrm{△OCD}\,\)は\(\,1\,\)辺が\(\,2\,\)の正三角形なので、
高さが\(\,\color{blue}{\sqrt{3}}\,\)になることから

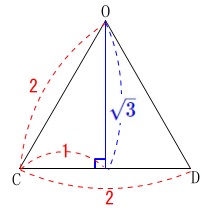
　\(\begin{eqnarray}
\mathrm{△OCD}&=&\frac{1}{2}\times \color{red}{2}\times \color{blue}{\sqrt{3}}\\
&=&\underline{　\sqrt{3}　}　(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

\(\,2018\,\)年長野県公立入試の数学は終わりです。

⇒　2018年(平成30年度)長野県公立高校入試数学問題の解説

前半の応用の少ない部分での配点に注意して、目標とする得点を決めたら時間配分を考えて問題全体をながめておくと良いですね。

もちろん、後半の応用問題も手を動かせば難しい問題ではありません。
ここで示した解法以外にも解き方はありますので、自分でいろいろと試してみて下さい。

⇒　中学数学を短期間で攻略する『覚え太郎』

短期間で基礎をおさえて、高いレベルで受験に対応した人にはお勧めです。

⇒　2019年(平成31年度)長野県公立高校入試の数学問題の解説

\(\,2019\,\)年度の長野県の数学問題と解説はこちらです。