2019年(平成31年度)に長野県で行われた公立高校入試の数学問題の解説です。
問1から問4までありますが、問題構成は2018年と変わりありません。
問1と問2は基本の確認のための小問集合になっています。ここで素早く処理して、時間と半分以上の点数を確保しておきましょう。
問題は長野県で公開してくれています。
問1
問\(\,1\,\)は小問集合で\(\,12\,\)問あります。
数の計算と数の大小
(1)正の数負の数から無理数までの計算です。
①
\(\hspace{10pt}2-4\\
=\underline{ -2 }\)
負の数の足し算は、数直線上で左に移動します。
⇒ 正の数負の数の大小を比較する数直線利用の練習問題と絶対値の意味
②
\(\hspace{10pt}\displaystyle \frac{2}{3}\times (-6)^2\\
\displaystyle =\frac{2\times 36}{3}\\
=\underline{ 24 }\)
分数のかけ算は約分をうまく利用するとはやいです。
③
\(\hspace{10pt}(\sqrt{3}+4)(\sqrt{3}-1)\\
=3-\sqrt{3}+4\sqrt{3}-4\\
=\underline{ -1+3\sqrt{3} }\)
すべてを展開をしますが、慣れていれば
\(\hspace{10pt}(\sqrt{3}+4)(\sqrt{3}-1)\\
=3+3sqrt{3}-4\\
=\underline{ -1+3sqrt{3} }\)
程度の暗算は良いですが、一気に答えという場合は慎重になる分余計に時間がかかったりしますので無理に暗算する必要はありません。
(2)数の大小は数直線上で見るとわかりやすいです。
ここでは最も小さい数を選ぶので、負の数だけを比較すれば良いですね。
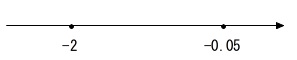\(-2\,＜\,-0.05\)
答え \(\,\underline{ イ }\,\)
合同条件と円周角の定理
(3)
合同条件をそろえるのに足りていない条件を答えます。
合同になることをいうには条件は3つ必要ですが、何を加えれば合同が言えるかです。
問題にある条件は、
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DEF}\,\)において
\(\mathrm{AB=DE}\,,\,\mathrm{BC=EF}\)
という2つの辺が等しいことです。
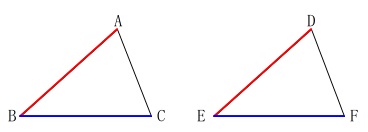あと何が条件に加われば合同が言えるかです。
合同条件を思い出せばすぐに出てきますが、
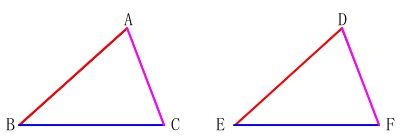3つめの辺が等しいこと
\(\mathrm{\color{magenta}{AC}=\color{magenta}{DF}}\)
を言うか、
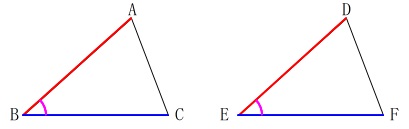等しい\(\,2\,\)辺の間の角が等しいこと
\(\mathrm{\color{magenta}{∠ABC}}=\mathrm{\color{magenta}{∠DEF}}\)
を言えば合同条件がそろいます。
答え \(\,\underline{ ア }\,,\,\underline{ ウ }\,\)
(4)
円と直径を含む三角形があるので円周角がもう一つ分かります。
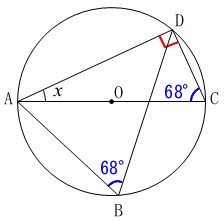
\(\mathrm{∠ADC}=\color{red}{90^{\circ}}\)
\(\mathrm{∠ABD=∠ACD}=\color{blue}{68^{\circ}}\)
三角形の内角の和が\(\,180^{\circ}\,\)であることから
\(\begin{eqnarray}
x+68^{\circ}&=&90^{\circ}\\
x&=&90^{\circ}-68^{\circ}\\
&=&\underline{ 22^{\circ} }
\end{eqnarray}\)
方程式と代入
(5)
方程式を解くときの基本的な方針は項をすべて左辺に集め、右辺を\(\,0\,\)にすることです。
\(\begin{eqnarray}
2x^2-2x&=&1-5x\\
2x^2-2x-1+5x&=&0\\
2x^2+3x-1&=&0
\end{eqnarray}\)
\(\,2\,\)次方程式を解くときは先ず因数分解を試すのですが、
因数分解できそうもないので解の公式ですね。
\(\begin{eqnarray}\displaystyle
x&=&\frac{-3\pm \sqrt{3^2-4\times 2\times (-1)}}{2\times 2}\\
&=&\frac{-3\pm\sqrt{9+8}}{4}\\
&=&\underline{ \frac{-3\pm\sqrt{17}}{4} }
\end{eqnarray}\)
(6)
問題に与えられる数値を代入するのは、代入する式をできるだけ簡単にしてからすると計算が楽になります。
⇒ 代入とは？文字式に代入するときのポイントと項と同類項(中学1年)
\(\hspace{10pt}5x-y-2(x-3y)\\
=5x-y-2x+6y\\
=3x+5y\\
\displaystyle =3\times \left(-\frac{1}{3}\right)+5\times \left(\frac{3}{5}\right)\\
\displaystyle =-1+3\\
=\underline{ 2 }\)
確率と関数の基本
(7)
同時に取り出しても、\(\,1\,\)枚ずつ取り出しても同じなので樹形図で良いですが、
組み合わせで考えて見ます。
\(\,0\,\)から\(\,4\,\)までの\(\,5\,\)枚のカードから\(\,2\,\)枚の取り出し方は、
\(\begin{array}{|c|c|c|} \hline
0 & 1 & \\ \hline
0 & 2 & \\ \hline
0 & 3 & \color{red}{○} \\ \hline
0 & 4 & \\ \hline
1 & 2 & \color{red}{○} \\ \hline
1 & 3 & \\ \hline
1 & 4 & \\ \hline
2 & 3 & \\ \hline
2 & 4 & \color{red}{○} \\ \hline
3 & 4 & \\ \hline
\end{array}\)
\(\,10\,\)通りあり、そのうち和が\(\,3\,\)の倍数になるのは\(\,\color{red}{○}\,\)の\(\,3\,\)通りです。
答え \(\,\displaystyle \underline{ \frac{3}{10} }\,\)
(8)
反比例を表す関数は比例定数を\(\,\color{red}{a}\,\)として、
\(\displaystyle y=\frac{\color{red}{a}}{x}\)
または
\(xy=\color{red}{a}\)
と表されます。
これは\(\,x\,\)と\(\,y\,\)の積が一定ということで、
双曲線上のと\(\,x\,\)軸\(\,y\,\)軸とでできる長方形の面積が常に一定ということを意味しています。
⇒ 比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方
\(\begin{eqnarray}
y&=&-\frac{4}{x}\\
xy&=&-4
\end{eqnarray}\)
\(\,x\,\)と\(\,y\,\)の積はいつも\(\,-4\,\)になります。
答え \(\,\underline{ ウ }\,\)
標本調査と三平方の定理
(9)
標本調査は、抽出した標本と母集団に比例関係が成り立つとして、推測することです。
はじめに箱の中に入っていた白い球を\(\,x\,\)とすると、
\(\,\color{blue}{200}\,\)個のオレンジ色の球を加えるので
全体が\(\,\color{red}{x+200}\,\)
となった状態で標本を取り出すと
\(\,\color{red}{70}\,\)個中\(\,\color{blue}{5}\,\)個がオレンジ
なので、
\(\begin{eqnarray}
\color{red}{70}:\color{blue}{5}&=&(\color{red}{x+200}):\color{blue}{200}\\
5(x+200)&=&70\times 200\\
x+200&=&\frac{70\times 200}{5}\\
&=&2800\\
x&=&2800-200\\
&=&\underline{ 2600 } (個)
\end{eqnarray}\)
推測なので答えとしては「およそ\(\,2600\,\)個」となります。
(10)
直角三角形の成立条件です。
直角三角形では\(\,3\,\)辺\(\,a,b,c\,\)において、
\(\,c\,\)を斜辺（\(\,3\,\)辺の中で一番長い辺）とすると
\(a^2+b^2=c^2\)（三平方の定理）
が成り立ちます。
逆に、
\(a^2+b^2=c^2\)
が成り立てば直角三角形であることが分かります。
この問題では「一番長い辺の長さは\(\,c\,\)」と書いてあるので、
\(\underline{ a^2+b^2=c^2\,が成り立てば良い。 }\)
で良いですが、何も書いていない場合は、
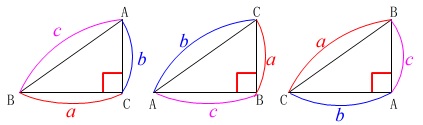
\(\color{red}{a^2}+\color{magenta}{c^2}=\color{blue}{b^2}\) （\(\,\mathrm{∠B=90^{\circ}}\,\)）
または
\(\color{blue}{b^2}+\color{magenta}{c^2}=\color{red}{a^2}\) （\(\,\mathrm{∠A=90^{\circ}}\,\)）
が成り立つとき、になります。
問\(\,1\,\)は以上ですが配点は小さくありませんので短時間で、確実に確保して高得点を目指しましょう。
問2
問\(\,2\,\)はデータの活用から作図や関数の利用の小問集合ですが、少し問題文が長くなります。
データの活用(代表値)
(1)
データの活用です。
代表値から売り上げから人数を求める方程式の利用まであります。
①
中央値は、値が小さい順に並べたときに度数の両端から真ん中にいる人の値です。
例えば、\(\,15\,\)人のデータがある場合、
\(\,7\,\)人｜\(\,8\,\)番目の人｜\(\,7\,\)人
\(\,8\,\)番目の人が真ん中になるので\(\,8\,\)番目の人の値が中央値です。
このデータでは\(\,120\,\)人分のデータがあるので、
小さい方から\(\,60\,\)人｜｜大きい方から\(\,60\,\)人
に分けられるので、小さい順（大きい順でも同じ）に並べたとき真ん中の人は、
\(\,60\,\)番目と\(\,61\,\)番目
なります。
このときは（偶数のとき）は真ん中の二人の平均を中央値とします。
図\(\,1\,\)の小さい方からの度数の合計を表す累積度数を見ていくと、
\(\begin{array}{|c|c|c|} \hline
\,個数\, & \,度数\, & \,累積度数\, \\ \hline
1 & 2 & \\ \hline
2 & 3 & 5 \\ \hline
3 & 11 & 16 \\ \hline
4 & 30 & 46 \\ \hline
\color{red}{5} & \color{red}{18} & \color{red}{64} \\ \hline
6 & 5 & 69 \\ \hline
7 & 6 & 75 \\ \hline
8 & 22 & 97 \\ \hline
9 & 15 & 112 \\ \hline
10 & 8 & 120 \\ \hline
\end{array}\)
\(\,60\,\)番目の人は\(\,5\,\)個
\(\,61\,\)番目の人も\(\,5\,\)個
なので中央値は\(\,\underline{ 5 }\,\)となります。
どちらも同じ個数なので平均を出す必要はありませんね。
※
「累積度数」は\(\,2021\,\)年度から正式採用される新課程教科書に追加される用語です。
⇒ 度数分布表とは？階級の幅と階級値および累積度数とヒストグラム
②
図\(\,1\,\)を見て、\(\,4\,\)個入りの箱を一番多く作る理由です。
買った人が最も多い（度数の最も多い）個数が入った箱が売れるだろうということで、
\(\,最頻値である\,4\,個入り\,\)
を多く作っておくという考えが出てきますね。
答え \(\,\underline{ 最頻値が\,4\,個だから。 }\,\)
方程式の利用
この問題は日曜日のデータとは関係がありません。
チョコレート\(\,1\,\)個は\(\,150\,\)円
\(\,2\,\)個買った人と\(\,3\,\)個買った人の人数合計は\(\,28\,\)人
金額の合計は\(\,10950\,\)円
この条件から\(\,2\,\)個買った人と\(\,3\,\)個買った人のそれぞれの人数を求める問題です。
方法は\(\,2\,\)つあります。
連立方程式として求めるか、\(\,1\,\)次方程式としてもとめるかです。
両方やっておきます。
（連立方程式を利用する場合）
\(\,2\,\)個買った人数を\(\,x\,\)人
\(\,3\,\)個買った人数を\(\,y\,\)人
とすると、
\(\,2\,\)個買った人の金額は
\(150\times 2\times x=300x\)
\(\,3\,\)個買った人の金額は
\(150\times 3\times y=450y\)
なので
\( \begin{cases}
\hspace{7pt} x+y=28\\ \\
\hspace{7pt} 300x+450y=10950
\end{cases}\)
これを解くと、
\(x=11\,y=17\)
答え
\(\,\underline{ 2\,個買った人数\,11\,人 }\,\)
\(\,\underline{ 3\,個買った人数\,17\,人 }\,\)
連立方程式の解き方は加減法でも代入法でもどちらでも良いです。
（\(\,1\,\)次方程式を利用する場合）
\(\,2\,\)個買った人数を\(\,x\,\)人とすると、
\(\,3\,\)個買った人数は\(\,(28-x)\,\)人となり、
金額はそれぞれ、
\(\,2\,\)個買う人は\(\,300\,\)円
\(\,3\,\)個買う人は\(\,450\,\)円
なので金額の合計が\(\,10950\,\)円であることから
\(300x+450(28-x)=10950\)
が成り立つ。
これを解いて、
\(\begin{eqnarray}
300x+450(28-x)&=&10950\\
300x+12600-450x&=&10950\\
300x-450x&=&10950-12600\\
-150x&=&-1650\\
x&=&\frac{1650}{150}\\
&=&11
\end{eqnarray}\)
これは\(\,2\,\)個買った人数で
\(\,3\,\)個買った人数は
\(\hspace{10pt}28-x\\
=28-11\\
=17\,\)
よって
\(\,\underline{ 2\,個買った人数\,11\,人 }\)
\(\,\underline{ 3\,個買った人数\,17\,人 }\,\)
対称と作図
(2)
対称な図形と作図の問題です。
図\(\,2\,\)の鶴は問題には関係ありません。
図\(\,3\,\)の条件を「明さんが気づいたこと」として書いてくれているので図示しておきます。
\(\,\mathrm{AC}\,\)と\(\,\mathrm{BD}\,\)の交点を\(\,\mathrm{O}\,\)とします。
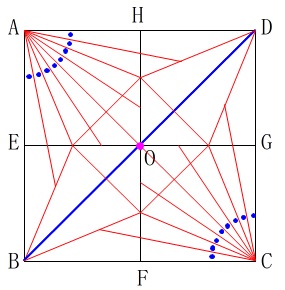数学で単に「対称」と言うときは線対称を意味します。
アからエまで、すべて見ていきましょう。
ア：\(\,\mathrm{HF}\,\)に対称か？
違います。
イ：\(\,\mathrm{BD}\,\)に対称か？
\(\,\mathrm{BD}\,\)を軸として対称です。
ウ：点\(\,\mathrm{O}\,\)を回転中心として\(\,90°\,\)回転した図形か？
頂点\(\,\mathrm{A}\,\)が\(\,\mathrm{B}\,\)または\(\,\mathrm{D}\,\)の位置に移動すると言うことなので重なりません。
エ：点\(\,\mathrm{O}\,\)を回転中心として\(\,180°\,\)回転した図形か？
頂点\(\,\mathrm{A}\,\)が\(\,\mathrm{C}\,\)に、頂点\(\,\mathrm{B}\,\)が\(\,\mathrm{D}\,\)の位置に移動するので重なります。
答え \(\,\underline{ イ , エ }\,\)
②
半直線などの基本用語を知らない人は『覚え太郎』をやりましょう。笑
この問題は図\(\,2\,\)図\(\,3\,\)を詳しく見る必要はありません。
角の二等分線を作図しなさいと言っているだけです。
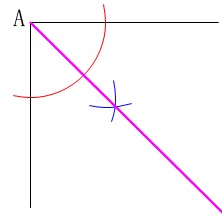半直線\(\,\mathrm{AC}\,\)は\(\,\mathrm{C}\,\)側にずっと続く線なので\(\,\mathrm{A}\,\)を始点に右側にはできるだけ長く書いておくと良いです。
2乗に比例する関数
(3)
振り子の往復にかかる時間（周期）は、
おもりの重さや振れ幅は関係ないということは有名な話ですが、
振り子の長さが変わると周期は変わります。
振り子の周期と振り子の長さとの関係は、
周期を\(\,\color{red}{x}\,(秒)\)
振り子の長さを\(\,\color{blue}{y}\,(\mathrm{m}\)
とすると、
\(\displaystyle \,\color{blue}{y}=\frac{1}{4}\color{red}{x^2}\,\)
の関係になります。
つまり、振り子の長さは周期の\(\,2\,\)乗に比例する関係です。
周期が振り子の長さの\(\,2\,\)乗に比例するのではないので注意して下さい。
①
周期が\(\,3\,\)倍になると振り子の長さは何倍になるか？
\(\,x\,\)が\(\,3\,\)倍になると\(\,\color{blue}{y}\,\)は何倍になるか？
なので \(\,3^2=\underline{ 9 }\,\)倍
②
振り子の長さが\(\,5.6\,\mathrm{m}\)の振り子時計の周期は何秒から何秒の範囲にあるか、という問題です。
言い換えると、
\(\displaystyle y=\frac{1}{4}x^2\)
において
\(\,y\,\)が\(\,5.6\,\)のときの\(\,x\,\)
を求めることになります。
\(\begin{eqnarray}
5.6&=&\frac{1}{4}x^2\\
22.4&=&x^2
\end{eqnarray}\)
この\(\,x\,\)は整数では求まりません。
\(\begin{eqnarray}
x^2&=&22.4\\
x&=&\pm\sqrt{22.4}
\end{eqnarray}\)
\(x\,＞\,0\)なので
\(\color{magenta}{x}=\color{magenta}{\sqrt{22.4}}\)
これを整数ではさめば良いだけです。
\(3=\sqrt{9}\)
\(\color{blue}{4}=\color{blue}{\sqrt{16}}\)
\(\color{red}{5}=\color{red}{\sqrt{25}}\)
なので
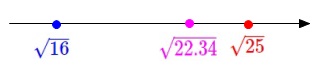
\(\color{blue}{\sqrt{16}}\,≦\,\color{magenta}{\sqrt{22.34}}\,＜\,\color{red}{\sqrt{25}}\)
だから
\(\color{blue}{4}\,≦\,\color{magenta}{x}\,＜\,\color{red}{5}\)
答え \(\,\underline{ 4\,秒以上\,5\,秒未満 }\,\)
ここまでで前半の問\(\,1\,\)問\(\,2\,\)は終了です。
⇒ 2018年(平成30年度)長野県公立高校入試数学問題の解説
\(\,2018\,\)年と同じように配点は半分以上あります。
基本的なことばかりですので後半の応用のためにチャチャとかたづけておきましょう。
教科書の基本的な問題を繰り返しておけば全部解ける問題ですよ。
⇒ 長野県公立高校入試2019年(平成31年度)の数学問題の解説【後半】
問\(\,3\,\)は\(\,1\,\)次関数の応用問題、問\(\,4\,\)は図形総合問題です。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
