長野県公立高校入試2019年(平成31年度)の数学問題の解説【後半】

2019年(平成31年度)に長野県で行われた公立高校入試の数学問題後半の解説です。
問3は1次関数の基本から応用まで、問4は図形総合問題です。
平面で問題は与えられていますが、回転体の体積もあり、図形の基本性質から線分比の応用まで幅広く出題されています。
問題をながめているだけでは答えにたどり着けませんよ。

問題は長野県で公開してくれています。

⇒　2019年長野県公立高校後期入試数学問題

問3.1次関数のグラフと応用問題

【問3】
数台のポンプを使って池の水を抜き取り、
その後、川から水をくみ上げて元に戻すのですが、
問題文と与えられた図を読み取るまでに時間を必要とします。

こういった長い文章問題は条件を簡単にまとめておくと良いです。

図\(\,1\,\)は見取り図ですがおおよそイメージできれば使いません。
使う関数は、時間と水面の高さの関数なので横幅は関係ありません。

階段状に作られた池なので高さが変わるということは、
　くみ上げる速さが途中で変わる
ということを頭において簡単に断面を書けば最後までさっと終わりますが、
問題の中で順序立てて質問してくれているので問題に合わせて答えていけば良いでしょう。

\(\,Ⅰ\,\)
ポンプ\(\,\mathrm{A}\,\)とポンプ\(\,\mathrm{B}\,\)を使いますが、くみ上げる能力は同じです。
ポンプ\(\,\mathrm{A}\,\)を\(\,2\,\)台使っていると考えて良いです。

　水面は\(\,\mathrm{120\,cm}\,\)の高さから下がりはじめる。
　水面の高さはポンプ\(\,2\,\)台使って\(\,20\,\)分後まで毎分\(\,\mathrm{3\,cm}\,\)下がる。
　\(\,20\,\)分後から水面は毎分\(\,\mathrm{6\,cm}\,\)下がる。
　
水面の高さ\(\,\mathrm{60\,cm}\,\)が変化のポイントになります。

毎分\(\,\mathrm{3\,cm}\,\)で\(\,20\,\)分間下がれば\(\,\mathrm{60\,cm}\,\)水面は下がります。
毎分\(\,\mathrm{6\,cm}\,\)で\(\,5\,\)分間下がれば\(\,\mathrm{30\,cm}\,\)水面は下がります。

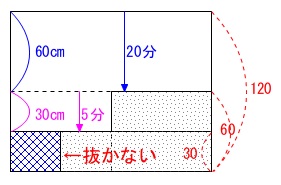
つまり、ポンプ\(\,2\,\)台使えば\(\,25\,\)分間で水面の高さは\(\,\mathrm{30\,cm}\,\)まで下がっているということです。

水面の高さの変化と変域と関係式

(1)
\(\,5\,\)分間で水面の高さがどれだけ下がったか？

最初の\(\,20\,\)分間は水面は毎分\(\,\mathrm{3\,cm}\,\)で下がります。

よって水を抜きはじめてから\(\,5\,\)分間で水面は

　\(3\times 5=\underline{　15　}　(\mathrm{cm})\)

下がります。

(2)
\(\,x\,\)の変域が\(\,20\,≦\,x\,≦\,25\,\)のとき

　毎分\(\,\mathrm{6\,cm}\,\)下がるので傾きは\(\,-6\,\)

なので

　\(y=-6x+b\)

とおけて

\(\,20\,\)分で高さが\(\,60\,\)になっているので

　\(\,(\,x\,,\,y)=(\,20\,,\,60\,)\,\)

を代入して

　\(\begin{eqnarray}
60&=&-6\times (20)+b\\
&=&-120+b\\
60+120&=&b\\
b&=&180
\end{eqnarray}\)

よって求める関係式は

　\(y=\underline{　-6x+180　}　(\,20\,≦\,x\,≦\,25\,)\)

または
　\(\,(\,20\,,\,60)\,,\,(\,25\,,\,30\,)\,\)
の\(\,2\,\)点を通ることから関係式を求めても良いですよ。

どちらかというと\(\,2\,\)点を通ることから求めるのが自然でしょう。

条件の読み取りと変化の起こる点

(3)
今度は途中でポンプが\(\,1\,\)つ壊れて止まってしまいます。
このとき、\(\,2\,\)台とも動いているときより時間がかかることを確認しておきましょう。

　\(\,14\,\)分後に確認したら水面の高さは\(\,\mathrm{\color{red}{90}\,cm}\,\)だった。

\(\,2\,\)台ともポンプが動いていたら

　\(3\times 14=42　(\,\mathrm{cm}\,)\)

下がっているはずなので

　\(\,120-42=\color{blue}{78}　(\,\mathrm{cm}\,)\,\)

になっていたはずです。

この差\(\,\color{red}{90}-\color{blue}{78}\,\)からポンプ\(\,\mathrm{A}\,\)が止まっていた時間は分かりますが、
問題が順序立てて聞いてくれているので問題を解いていきましょう。

①
\(\,14\,\)分の段階で水面の高さは\(\,\mathrm{90\,cm}\,\)でした。
そこから\(\,20\,\)分までの\(\,6\,\)分間はポンプ\(\,1\,\)台で水を抜くことになります。

ポンプ\(\,1\,\)台だと\(\,2\,\)台のときの半分、毎分\(\,\mathrm{1.5\,cm}\,\)水面の高さは下がるので、

　\(1.5\times 6=9　(\,\mathrm{cm}\,)\)

水面の高さは下がります。

よって\(\,20\,\)分後の水面の高さは

　\(90-9=\underline{　81　}　(\,\mathrm{cm}\,)\)

②
ポンプ\(\,\mathrm{A}\,\)が壊れたのが水を抜きはじめて\(\,x\,\)分だとします。

　\(\,2\,\)台で水を抜いた時間は\(\,x\,\)分間。
　\(\,1\,\)台で水を抜いた時間は\(\,(14-x)\,\)分間。
　\(\,x\,\)分間は毎分\(\,\mathrm{3\,cm}\,\)水面の高さは下がる。
　\(\,(14-x)\,\)分間では毎分\(\,\mathrm{1.5\,cm}\,\)水面の高さは下がる。
　水を抜きはじめて\(\,14\,\)分間で下がった水面の高さは\(\,\mathrm{30\,cm}\,\)。

これを方程式にすると、

　\(3x+1.5(14-x)=30\)

これを解いて

　\(\begin{eqnarray}\displaystyle
3x+1.5(14-x)&=&30\\
3x+21-1.5x&=&30\\
3x-1.5x&=&30-21\\
1.5x&=&9\\
15x&=&90\\
x&=&\frac{90}{15}\\
&=&\underline{　6　}　(分後)
\end{eqnarray}\)

先ほど少し触れましたが\(\,2\,\)台で水を抜いたときとの差は
　\(\color{red}{90}-\color{blue}{78}=\,\mathrm{\color{magenta}{12}\,cm}\,\)
でした。

ポンプ\(\,2\,\)台で水を抜いた場合と、ポンプ\(\,1\,\)台で水を抜いた場合とでは、
毎分\(\,\mathrm{1.5\,cm}\,\)の違いがあるので、

　\(\hspace{10pt}\displaystyle \color{magenta}{12}\div 1.5\\
\displaystyle =\frac{12}{1.5}\\
\displaystyle =\frac{120}{15}\\
=8　(分間)\)

ポンプ\(\,\mathrm{A}\,\)は止まっていたことになります。

よって、ポンプ\(\,\mathrm{A}\,\)が止まったのは水を抜きはじめてから
　\(14-8=\underline{　6　}　(分後)\)

と求めることもできます。

③
ポンプ\(\,\mathrm{A}\,\)が壊れているので後はポンプ\(\,1\,\)台で水を抜くことに注意しておきましょう。

\(\,\mathrm{120\,cm}\,\)ある水を\(\,\mathrm{60\,cm}\,\)を経て\(\,\mathrm{30\,cm}\,\)にすることは忘れないようにしましょう。

①で\(\,\mathrm{120\,cm}\,\)から\(\,\mathrm{81\,cm}\,\)まで\(\,\color{red}{20}\,\)分かかっています。

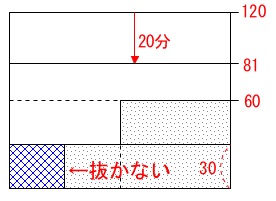
水面の高さが\(\,\mathrm{81\,cm}\,\)から\(\,\mathrm{60\,cm}\,\)まではポンプ\(\,1\,\)台で抜き出すので毎分\(\,\mathrm{1.5\,cm}\,\)下がることから

　\(\hspace{10pt}\displaystyle \frac{81-60}{1.5}\\
\displaystyle =\frac{21}{1.5}\\
=\color{blue}{14}　(分)\)

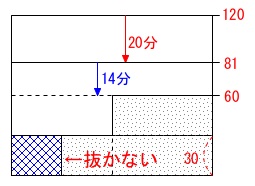
水面の高さが\(\,\mathrm{60cm}\,\)から\(\,\mathrm{30cm}\,\)までは、
ポンプ\(\,2\,\)台の場合の毎分\(\,\mathrm{6\,cm}\,\)の半分で毎分\(\,\mathrm{3\,cm}\,\)下がるので、

　\(\hspace{10pt}\displaystyle \frac{60-30}{3}\\
=\color{magenta}{10}　(分)\)

かかります。

合わせると全体で

　\(\hspace{10pt}\color{red}{20}+\color{blue}{14}+\color{magenta}{10}\\
=44　(分)\)

かかりました。

ポンプ\(\,2\,\)台の昨年は\(\,25\,\)分で\(\,\mathrm{30\,cm}\,\)の高さまで水を抜けいていたので、

　\(\hspace{10pt}44-25\\
=\underline{　19　}　(分)\)

昨年より遅かったことになります。

グラフと座標の読み取り

\(\,Ⅱ\,\)
今度は違うポンプ\(\,\mathrm{C}\,\)を使って水を入れます。

水面の高さは上がりますが、ここでも\(\,\mathrm{60\,cm}\,\)が変化するポイントです。

(1)
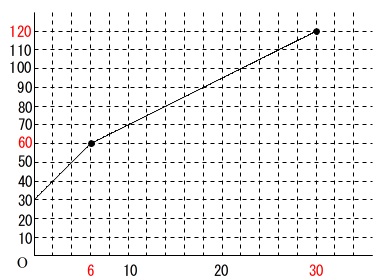
グラフを読み取ると\(\,2\,\)分間で\(\,\mathrm{10\,cm}\,\)上昇しているので、
\(\,6\,\)分後に水面の高さは\(\,\mathrm{30\,cm}\,\)上昇し、\(\,\mathrm{60\,cm}\,\)になります。
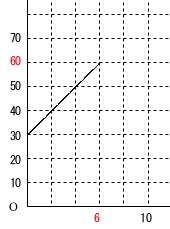この後は水をくみ出すときと同じで高さの上昇は半分になります。

水面の高さ\(\,\mathrm{60\,cm}\,\)から\(\,\mathrm{120\,cm}\,\)までは\(\,2\,\)分間で\(\,\mathrm{5\,cm}\,\)上昇します。
\(\,1\,\)分間では\(\,\mathrm{2.5\,cm}\,\)です。

\(\,\mathrm{60\,cm}\,\)上昇して\(\,\mathrm{120\,cm}\,\)になるまでには
　\(\hspace{10pt}\displaystyle \frac{60}{2.5}=24\,分\)かかる
ので、\(\,30\,\)分後に\(\,\mathrm{120\,cm}\,\)になります。

よって、答えは下のグラフになります。

(2)
水を入れはじめて水面の高さが\(\,\mathrm{100\,cm}\,\)になるまでの時間をグラフを用いて求める方法は、
\(\,y\,\)座標が水面の高さを表しているので、

　\(\underline{　y=100\,になるときの\,x\,を読み取れば良い。　}\)
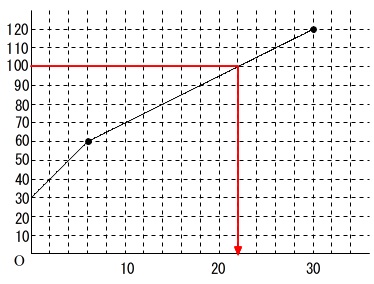実際に時間を求める必要はありませんが、実際に求めるときはグラフの読み取りより関数として求めた方が確実ですよ。

　\((\,6\,,\,60\,)\,,\,(\,30\,,\,120\,)\)

を通るので直線の式は、

　\(\displaystyle y=\frac{5}{2}x+45\)

なので\(\,y=100を\,\)代入して、

　\(\begin{eqnarray}\displaystyle
100&=&\frac{5}{2}x+45\\
200&=&5x+90\\
110&=&5x\\
22&=&x
\end{eqnarray}\)

この問題はグラフから読み取る方法を答えれば良いので、必要ないです。

問4.図形の総合問題

【問4】
線分の長さ、回転体の体積、平行四辺形の性質、相似の証明、正三角形と三平方の定理を利用した線分の長さ、線分比を応用した面積を求める問題がそろった図形総合問題です。

条件を見落とさないように、一つひとつ目で確認しながら進めると良いですよ。

\(\,Ⅰ\,\)
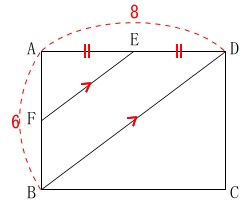
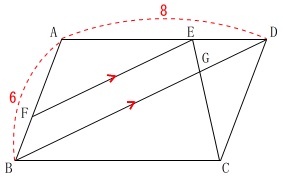
図\(\,1\,\)は長方形と平行線でできた図形です。

条件
　
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{AD=8}\,\)
　\(\,\mathrm{E}\,\)は線分\(\,\mathrm{AD}\,\)の中点
　\(\,\mathrm{EF\,/\!/\,BD}\,\)
　

線分の長さと回転体の体積

(1)
　\(\,\mathrm{EF\,/\!/\,BD}\,\)なので\(\,\mathrm{F}\,\)は\(\,\mathrm{AB}\,\)の中点です。

三平方の定理を\(\,\mathrm{△AEF}\,\)に直接利用できます。

　\(\begin{eqnarray}
\mathrm{EF^2}&=&\mathrm{AE^2+AF^2}\\
&=&4^2+3^2\\
&=&16+9\\
&=&25\\
\mathrm{EF}&=&\underline{　5　(\mathrm{cm})}　(\,\mathrm{EF}\,＞\,0\,)
\end{eqnarray}\)

(2)
軸を\(\,\mathrm{DE}\,\)とした四角形\(\,\mathrm{BDEF}\,\)の回転体は、
\(\,\mathrm{△ABD}\,\)を回転させた三角錐から\(\,\mathrm{△AFE}\,\)を回転させた三角錐をくり抜いた形をしています。

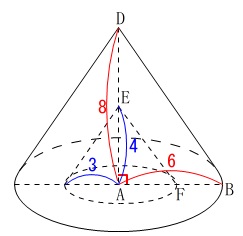
\(\,\mathrm{△ABD}\,\)を回転させた三角錐の体積\(\,\mathrm{\color{red}{V_1}}\,\)は、

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{V_1}}&=&\frac{1}{3}\times 6^2\,\pi\times 8\\
&=&96\,\pi
\end{eqnarray}\)

\(\,\mathrm{△AFE}\,\)を回転させた三角錐の体積\(\,\mathrm{\color{blue}{V_2}}\,\)は、

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{V_2}}&=&\frac{1}{3}\times 3^2\,\pi\times 4\\
&=&12\,\pi
\end{eqnarray}\)

よって求める立体の体積は、

　\(\begin{eqnarray}
\mathrm{\color{red}{V_1}-\color{blue}{V_2}}&=&96\,\pi-12\,\pi\\
&=&\underline{　84\,\pi　}　(\mathrm{cm^2})
\end{eqnarray}\)

平行四辺形の性質と相似の証明

\(\,Ⅱ\,\)
図\(\,2\,\)は図\(\,1\,\)の長方形が平行四辺形になります。

条件
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{AD=8}\,\)
　\(\,\mathrm{BD\,/\!/\,FE}\,\)
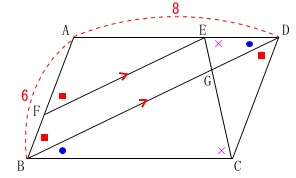
平行線の性質から等しい角（同位角、錯角）を示しておきます。

(1)
\(\,\mathrm{∠ABD}\,\)と等しい角は、同位角と錯角の

　\(\mathrm{∠AFE}　と　\mathrm{∠BDC}\)

答え　\(\,\underline{　ウ　,　エ　}\,\)

(2)
\(\,\mathrm{△GBC}\,\)と\(\,\mathrm{△GDE}\,\)が相似な図形であることを証明しますが、すでに図の中で済ませてあります。

（証明）
　\(\,\mathrm{△GBC}\,\)と\(\,\mathrm{△GDE}\,\)において
四角形\(\,\mathrm{ABCD}\,\)は平行四辺形なので対辺が平行だから
　\(\,\mathrm{∠GBC=∠GDE}\,\)　(平行線の錯角)　･･･①
　\(\,\mathrm{∠GCB=∠GED}\,\)　(平行線の錯角)　･･･②
①②より
　\(\,2\,\)組の角がそれぞれ等しい
ので
　\(\,\mathrm{△GBC}\,\)　≡　\(\,\mathrm{△GDE}\,\)
（終わり）

錯角2つを使いましたが、相似条件の1つは
　対頂角\(\,\mathrm{∠BGC=∠DGE}\,\)
でも良いですよ。

正三角形の性質と三平方の定理

(3)
図\(\,2\,\)の平行四辺形において\(\,\mathrm{△CDE}\,\)が正三角形の場合です。
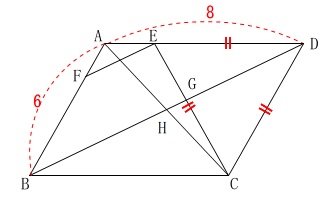四角形\(\,\mathrm{ABCD}\,\)は平行四辺形なので

　\(\mathrm{AB=DC=DE=CE=\color{blue}{6}}\)
①
\(\,\mathrm{BD}\,\)の長さを求めますが、
　\(\,\mathrm{C}\,\)から直線\(\,\mathrm{AD}\,\)と、
　\(\,\mathrm{D}\,\)から直線\(\,\mathrm{BC}\,\)に、
垂線を引けば三角定規が出てくるのですぐに求まります。

　\(\,\mathrm{CI　⊥　AD}\,\)
　\(\,\mathrm{DJ　⊥　BC}\,\)
となるように\(\,\mathrm{I,J}\,\)をとると
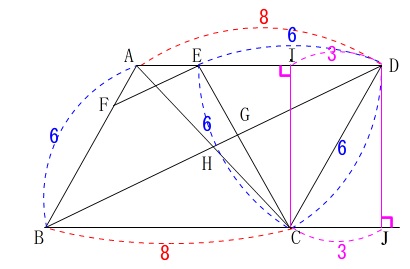\(\,\mathrm{△CDI}\,\)と\(\,\mathrm{△DCJ}\,\)合同で三角定規なので

　\(\begin{eqnarray}
\mathrm{CJ:DJ}&=&1:\sqrt{3}\\
3:\mathrm{DJ}&=&1:\sqrt{3}\\
\mathrm{DJ}&=&\color{magenta}{3\sqrt{3}}
\end{eqnarray}\)

必要ありませんが\(\,\mathrm{CI}\,\)も同じ長さで

　\(\mathrm{CI=DJ}=\color{magenta}{3\sqrt{3}}\)

です。
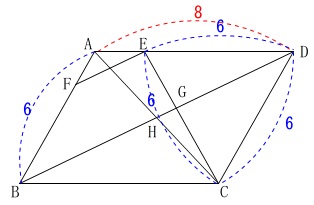
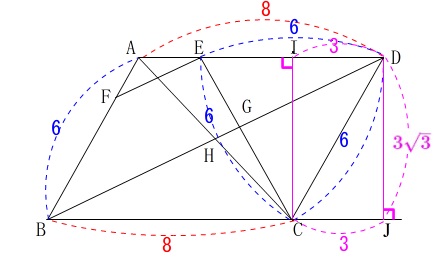\(\,\mathrm{△BDJ}\,\)に三平方の定理を用いると、
　\(\begin{eqnarray}
\mathrm{BJ}&=&\mathrm{BC+CJ}\\
&=&\color{red}{8}+\color{magenta}{3}\\
&=&11
\end{eqnarray}\)

なので

　\(\begin{eqnarray}
\mathrm{BD^2}&=&\mathrm{BJ^2+DJ^2}\\
&=&11^2+(3\sqrt{3})^2\\
&=&121+27\\
&=&148
\end{eqnarray}\)

\(\,148\,\)を素因数分解すると

　\(2\underline{)\,148}\\
2\underline{)\hspace{6pt}74}\\
\hspace{16pt}37\)

よって

　\(\mathrm{BD}=\underline{　2\sqrt{37}　}　(\mathrm{cm})\)

線分比の応用と三角形の面積

②\(\,\mathrm{△CGH}\,\)の面積を求めます。
底辺と高さとなる辺を持たないので線分比を利用した縮小です。
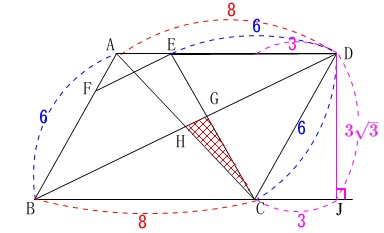基準にするのは平行四辺形\(\,\mathrm{ABCD}\,\)で良いですね。
面積が具体的に求まるので基準は\(\,\mathrm{△BCD}\,\)でも良いですよ。

底辺は\(\,\mathrm{BC=8}\,\)、高さは\(\,\mathrm{DH=3\sqrt{3}}\,\)と見ると

　\(\begin{eqnarray}
(四角形\mathrm{ABCD})&=&8\times 3\sqrt{3}\\
&=&\color{red}{24\sqrt{3}}
\end{eqnarray}\)

ここで相似な三角形から
　\(\,\mathrm{△BGC}\,\)　∽　\(\,\mathrm{△DGE}\,\)
で相似比が
　\(\,8:6=\color{red}{4}:\color{red}{3}\,\)

また合同な三角形から
　\(\,\mathrm{△BHC}\,\)　≡　\(\,\mathrm{△DHA}\,\)
だから
　\(\,\mathrm{BH:HD=\color{blue}{1}:\color{blue}{1}}\,\)
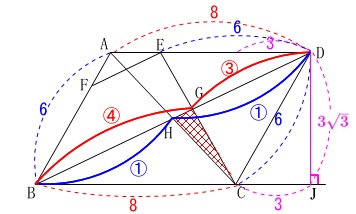\(\,\mathrm{GH}\,\)と\(\,\mathrm{BD}\,\)との比が知りたいので分かり易くするため、
線分\(\,\mathrm{BD}\,\)を抜き出して見ておきます。
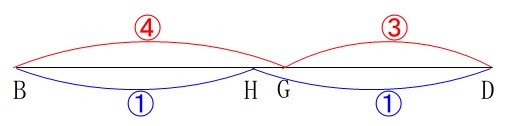これでは\(\,\mathrm{HG}\,\)と\(\,\mathrm{BD}\,\)の線分比が出しにくいので線分\(\,\mathrm{BD}\,\)を都合の良い値で設定します。

　\(\,\color{red}{④}+\color{red}{③}=\color{magenta}{⑦}\,\)　と　\(\,\color{blue}{①}+\color{blue}{①}=\color{magenta}{②}\,\)

の最小公倍数を利用して、

　\(\,\mathrm{BD}=\color{magenta}{⑭}\,\)

とすると、

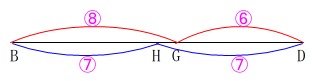
　\(\,\mathrm{BH:HG:GD}=\color{magenta}{⑦}:\color{magenta}{①}:\color{magenta}{⑥}\,\)

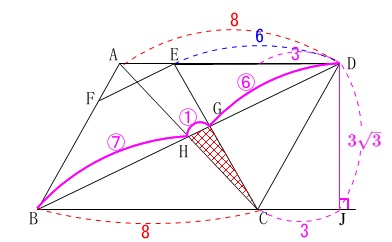
\(\,\mathrm{△BCD}\,\)の面積は平行四辺形の\(\,\displaystyle \frac{1}{2}\,\)で、
\(\,\mathrm{△CGH}\,\)の面積はその\(\,\displaystyle \color{magenta}{\frac{1}{14}}\,\)になります。

平行四辺形\(\,\mathrm{ABCD}\,\)の面積は\(\,\color{red}{24\sqrt{3}}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{△CGH}&=&\color{red}{24\sqrt{3}}\times \frac{1}{2}\times \frac{1}{14}\\
&=&\underline{　\frac{6\sqrt{3}}{7}　}　(cm^2)
\end{eqnarray}\)

『覚え太郎』会員なら、相似比から

　\(\,\mathrm{CH:AH=1:1}\,\)
　\(\,\mathrm{CG:FG=4:3}\,\)

また

　\(\begin{eqnarray}
\mathrm{\color{blue}{△ACE}}&=&\mathrm{△ACD}\times \frac{2}{8}\\
&=&\frac{1}{2}\times 8\times 3\sqrt{3}\times \frac{1}{4}\\
&=&\color{blue}{3\sqrt{3}}
\end{eqnarray}\)

なので、

　\(\begin{eqnarray}\displaystyle
\mathrm{△CGH}&=&\mathrm{\color{blue}{△ACE}}\times \frac{1}{1+1}\times \frac{4}{3+4}\\
&=&\color{blue}{3\sqrt{3}}\times \frac{1}{2}\times \frac{4}{7}\\
&=&\underline{　\frac{6\sqrt{3}}{7}　}
\end{eqnarray}\)

としても良いですよ。
『超え太郎』－「相似な図形\(\,\mathrm{No.60}\,\)」を利用しました。

\(\,2019\,\)年の長野県公立高校入試の問題は以上です。

⇒　2020年(令和2年)度長野県公立高校入試の数学の問題と解説

時間配分を考えて、手を動かせば十分高得点が狙えます。

⇒　長野県公立高校入試数学の問題と解説

傾向は大きくは変わらないので、全体の構成と何をすべきか見ておくと良いですね。