2020年(令和2年)度長野県公立高校入試の数学の問題と解説

2020年(令和2年)度に実施された長野県公立高校入試の数学の問題と解説です。
問題は大きく４問あり、偏った分野はなく中学の数学全般からの出題になっています。
計算力によって差が出ることはありませんが、
記述解答がいくつかあるので誤字脱字には気をつけておきましょう。

2020年(令和2年)度長野県公立高校入試の数学の問題と解説

問１から問４までの１００点満点の問題です。
考え方を表現する問題が割と多いのでそれぞれ解説しますが、
文字式計算などを省略する場合があるので、
行間はご自分でうめながら読み進めてください。

2020年(令和2年)度長野県公立高校入試の数学の問題

長野県で公開してくれている令和２年度県立高校入試の数学の問題です。

⇒　令和2年度長野県立高校入試数学の問題

ページ数が多いので焦るかもしれませんが、
問題文をしっかり読み取り、
問題の指示通りに進めれば確実に先に進めることができる問題です。

2020年(令和2年)度長野県公立高校入試の数学の解説

記述解答がいくつかあります。
一字一句解答と同じでなければダメということではありませんので、
論理的にまとめてあれば自分の言葉で構いません。
ただし、誤字脱字は減点されます。
問題量に対して時間に余裕はあるのでしっかり見直ししましょう。
（私は誤字脱字を気にせず解説するのであればご指摘ください。）

解説がいつも長くなるので余計なことは書かず、
早速問題解説に入ります。

問１

【問 1】

(1)
　\(\hspace{10pt}3-(-5)\\
=3+5\\
=\underline{　8　}\)

負の数を引くと足すことになります。

(2)
　\(\hspace{10pt}-4^2\\
=\underline{　-(4\times 4)　}\\
=-16\)

（かっこ）の省略に気を配って計算しているかどうかを聞いています。

答え　\(\,\underline{　ウ　}\,\)

(3)
　\(\begin{eqnarray}\displaystyle
2(x-1)&=&-6\\
2x-2&=&-6\\
2x&=&-6+2\\
&=&-4\\
x&=&\underline{　-2　}
\end{eqnarray}\)

方程式を処理するときは基本的には左辺にすべての項を集めることですが、
例外の1つに\(\,1\,\)次方程式があります。
ここは気にせず今まで通り定数項を右辺に集めましょう。

(4)
　\(\hspace{10pt}\displaystyle \color{red}{\sqrt{75}}-\frac{9}{\sqrt{3}}\\
\displaystyle =\color{red}{5\sqrt{3}}-\frac{9\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}\\
\displaystyle =5\sqrt{3}-\frac{9\times \sqrt{3}}{3}\\
=5\sqrt{3}-3\sqrt{3}\\
=\underline{　2\sqrt{3}　}\)

分母の有理化部分は上記の通りですが、
\(\,\color{red}{75}\,\)の素因数分解は確実にやりましょう。

(5)
奇数は\(\,2\,\)で割り切れない整数です。

アの\(\,n+1\,\)は\(\,n\,\)が奇数の場合偶数になります。
イの\(\,2n\,\)は偶数そのものを表しています。
ウの\(\,2n+1\,\)は偶数の次の数を意味するので奇数です。
エの\(\,2n+3=2(n+1)+1\,\)も同様に奇数です。
（\(\,(偶数)+(奇数)\,\)なので奇数、でも良いです。）
オの\(\,3n\,\)は\(\,n\,\)が偶数の場合偶数になります。

答え　\(\,\underline{　ウ　,　エ　}\,\)

整数で偶数の次に来る数が奇数です。

(6)
展開公式を利用する典型的な計算です。
　\(\hspace{4pt}(\color{red}{a}-\color{blue}{b})(\color{red}{a}+\color{blue}{b})=\color{red}{a}^2-\color{blue}{b}^2\)
を利用します。

　\(\hspace{4pt}698=\color{red}{700}-\color{blue}{2}\)
　\(\hspace{4pt}702=\color{red}{700}+\color{blue}{2}\)
なので
　\(\begin{eqnarray}
698\times 702&=&(\color{black}{\fbox{700}}-\color{black}{\fbox{2}})(\color{black}{\fbox{700}}+\color{black}{\fbox{2}})\\
&=&\color{black}{\fbox{700}}^2-\color{black}{\fbox{2}}^2\\
&=&490000-4\\
&=&489996
\end{eqnarray}\)

答え　\(\,あ　\underline{　700　}\,\)　\(\,い　\underline{　2　}\,\)

(7)
\(\,y\,\)が\(\,x\,\)に反比例するので
　\(\displaystyle y=\frac{a}{x}\)
とおいて比例定数を決めましょう。

反比例は
　\(\hspace{4pt}xy=a\)
でもあるので\(\,x=1\,,\,y=-16\,\)を満たすことから
　\(\hspace{4pt}a=1\times (-16)=-16\)
このとき反比例の関数は
　\(\hspace{10pt}\displaystyle y=\frac{-16}{x}\)
なので\(\,x=3\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{-16}{3}\\
&=&\underline{　-\frac{16}{3}　}
\end{eqnarray}\)

(8)
\(\,y\,\)の変域は最小値と最大値の範囲です。
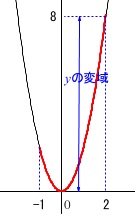最小値、最大値に\(\,x=-1\,\)のときの\(\,y\,\)の値は関係ありません。
\(\,-1\,≦\,x\,≦\,2\,\)のときの\(\,y\,\)の変域は
　\(\hspace{10pt}0\,≦\,y\,≦\,8\)

答え　\(\,\underline{　ア　}\,\)

問題にグラフがなくてもグラフを簡単なもので良いので書いて確認しましょう。

(9)
樹形図を書いてくれているので、
樹形図の横に表が出たときの金額を書き出せば終わりです。

表で確認しておきます。
　\(\begin{array}{|c|c|c|c|} \hline
100 & 50 & 10 & \,金額\, \\ \hline
○ & ○ & ○ & \color{red}{160} \\ \hline
○ & ○ & × & \color{red}{150} \\ \hline
○ & × & ○ & \color{red}{110} \\ \hline
○ & × & × & 100 \\ \hline
× & ○ & ○ & 60 \\ \hline
× & ○ & × & 50 \\ \hline
× & × & ○ & 10 \\ \hline
× & × & × & 0 \\ \hline
\end{array}\)

答え　\(\displaystyle \underline{　\frac{3}{8}　}\)

(10)
対称の軸\(\,\ell\,\)を作図します。

　\(\,\mathrm{A}\,\)が\(\,\mathrm{C}\,\)に
　\(\,\mathrm{B}\,\)が\(\,\mathrm{D}\,\)に
対称移動するのでどちらでも良いので、
移動する前と後の点を結んだ線分の
　「垂直二等分線」
を作図すればそれが\(\,\ell\,\)です。
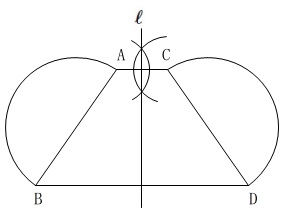\(\,\mathrm{AC}\,\)を使った場合は\(\,\mathrm{BD}\,\)を結ぶ必要はありません。

単に「対称」というときは通常「線対称」のことです。

(11)
角度と四角形の周の長さを求めます。

条件
　\(\,\mathrm{AB,BC}\,\)の中点を\(\,\mathrm{M,N}\,\)とする。
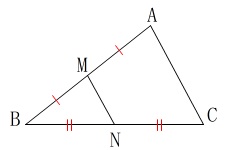唯一の条件、中点連結定理から
　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{MN}\,\)
　\(\,\mathrm{AC=2MN}\,\)
は使うと考えていて良いです。

①
\(\,\mathrm{∠A=80^{\circ}}\,\)のとき、
\(\,\mathrm{∠BMN}\,\)の大きさを求めます。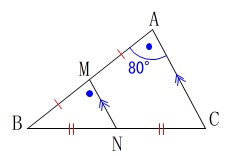　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{MN}\,\)
なので同位角が等しくなります。

　\(\hspace{10pt}\mathrm{∠BMN}=\underline{　80^{\circ}　}\)

②
四角形\(\,\mathrm{AMPC}\,\)の周の長さを求めます。

①に条件が加わります。
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{CP}\,\)
　\(\,\mathrm{AB=8}\,\)
　\(\,\mathrm{AC=6}\,\)
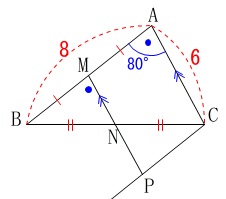四角形\(\,\mathrm{AMPC}\,\)は平行四辺形なので、
\(\,\mathrm{M}\,\)が\(\,\mathrm{AB}\,\)の中点だから
　\(\,\mathrm{AM=CP=4}\,\)
　\(\,\mathrm{AC=MP=6}\,\)
よって
　\(\hspace{10pt}4\times 2+6\times 2\\
=8+12\\
=\underline{　20　\mathrm{cm}}\)

問２

【問 2】
データの活用と図形と方程式の問題です。

(1)
度数分布表の読み取りです。
　\(\begin{array}{|c|c|c|} \hline
　時間　 & 中学生 & 高校生 \\ \hline
0\,～\,1 & 401 & 182 \\ \hline
1\,～\,2 & \color{blue}{262} & \color{blue}{340} \\ \hline
2\,～\,3 & 178 & \color{red}{374} \\ \hline
3\,～\,4 & 68 & 264 \\ \hline
4\,～\,5 & 41 & 115 \\ \hline
5\,～\,6 & 50 & 225 \\ \hline
　計　& 1000 & 1500 \\ \hline
\end{array}\)

①
高校生の度数が最も多い階級を求めます。
高校生の度数が一番多いのは\(\,\color{red}{374}\,\)です。

答え
　\(\underline{　2　}\,\)時間以上\(\,\,\underline{　3　}\,\,\)時間未満の階級

②
高校生の\(\,1\,\)時間以上\(\,2\,\)時間未満の階級の相対度数を求めます。
　\(\hspace{10pt}\displaystyle \frac{340}{1500}\\
=0.2266\cdots\)

小数第\(\,3\,\)位を四捨五入すると
　\(\hspace{10pt}\underline{　0.23　}\)

　\(\displaystyle (相対度数)=\frac{　(度数)　}{　(度数合計)　}\)
です。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表の読み取り問題は今後も出題され続けます。

③
\(\,1\,\)時間以上\(\,2\,\)時間未満の階級の割合を比較し、
割合が大きい方を選びます。

　\(\hspace{10pt}\displaystyle \frac{262}{1000}\\
=0.262\)
なので中学生の相対度数は\(\,0.26\,\)

②から高校生の相対度数は\(\,0.23\,\)

「相対度数が大きいので中学生の方が割合が大きい」
ということです。

答え　\(\,\underline{　ア　}\,\)

(2)
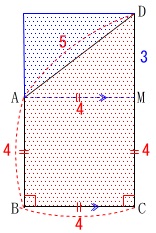
円柱を切り取ったときの見取り図と投影図があります。

条件
　\(\,\mathrm{P}\,\)は円柱を斜めに切り取った立体
　底面の円の半径は\(\,2\,\)
投影図において
　\(\,\mathrm{AD=5}\,\)
　\(\,\mathrm{AB=BC}\,\)
　\(\,\mathrm{∠B=∠C=90^{\circ}}\,\)
（長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）
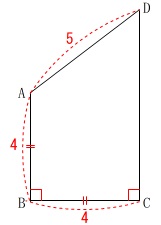底面の半径が\(\,2\,\)なので、
\(\,\mathrm{BC}\,\)は底面の円の直径だから
　\(\,\mathrm{BC=4}\,\)
となっています。

①
\(\,\mathrm{ＣＤ}\,\)の長さを求めます。

\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に平行な線を引くと正方形ができます。
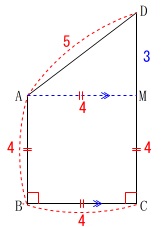\(\,\mathrm{△AMD}\,\)は\(\,3:4:5\,\)の直角三角形なので
　\(\,\mathrm{DM=3}\,\)

よって、
　\(\begin{eqnarray}
\mathrm{ＣＤ}&=&\mathrm{ＣＭ+ＭＤ}\\
&=&\color{red}{4}+\color{blue}{3}\\
&=&\underline{　7　\mathrm{cm}}
\end{eqnarray}\)

\(\,\mathrm{△AMD}\,\)の比を知らない場合は三平方の定理で簡単に出ます。
　\(\begin{eqnarray}\displaystyle \displaystyle
\mathrm{DM}&=&\mathrm{\sqrt{AD^2-AM^2}}\\
&=&\sqrt{5^2-4^2}\\
&=&\sqrt{25-16}\\
&=&\sqrt{9}\\
&=&3
\end{eqnarray}\)

②
\(\,\mathrm{P}\,\)の体積を求めます。

円柱を切った残りを足すと円柱になります。
そこで\(\,\mathrm{P}\,\)をもう一つ上にひっくり返して足すと、
底面は同じで高さが\(\,2\,\)倍の円柱ができます。
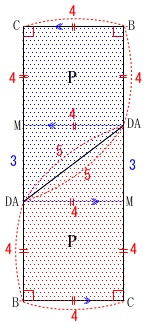この円柱の体積は\(\,\mathrm{P}\,\)の体積\(\,V\,\)の\(\,2\,\)倍で、
底面積は半径\(\,2\,\)の円なので
　\(\begin{eqnarray}\displaystyle
2V&=&\pi\times (2)^2\times (4+3+4)\\
&=&44\,\pi
\end{eqnarray}\)

よって、\(\,\mathrm{P}\,\)の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{2}\times 44\,\pi\\
&=&\underline{　22\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

もちろん、
高さ\(\,3\,\)の円柱の半分を下の高さ\(\,4\,\)の円柱に足しても良いです。
それほど時間に差が出る問題ではありませんので、
思い立った方針で突っ走って構いません。

(3)
\(\,2\,\)次方程式が利用ができる計算方法です。

「塵劫記（じんこうき）」という江戸時代の書物が紹介されていますが関係ありません。
江戸時代から数学は利用されていて、進化しているということがわかれば良いです。　

俵の総数を表す関係式は
　\((\,1\,列の俵の数)\times (段の数)\div 2\)
です。

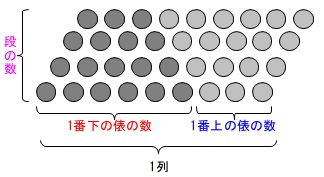
\(\,1\,\)列の数は
　\(\,(\color{red}{\,1\,番下の俵の数})+(\color{blue}{\,1\,番上の俵の数})\,\)

段の数は
　\(\,(\color{red}{\,1\,番下の俵の数})-(\,\color{blue}{1\,番上の俵の数}-1)\,\)

①
\(\,1\,\)番下の俵の数が\(\,\color{red}{8}\,\)、
\(\,1\,\)番上の俵の数が\(\,\color{blue}{4}\,\)ときの「計算式」を表します。

　\(\hspace{10pt}(8+4)\times (8-3)\div 2\\
=\underline{　12\times 5\div 2　}\)

俵の総数を文字を使って表すと分かり易いです。

　\(\,1\,\)番下の段の数を\(\,m\,\)
　\(\,1\,\)番上の段の数を\(\,n\,\)
とすると俵の数は
　\(\hspace{10pt}(m+n)(m-n+1)\div 2\\
=\displaystyle \frac{(m+n)(m-n+1)}{2}\)

②ではこの課程を自分でやっておくことが求められます。

②
俵の総数が\(\,60\,\)個、\(\,1\,\)番上の俵の数が\(\,4\,\)のとき、
\(\,1\,\)番下の俵の数を求めます。

\(\,1\,\)番下の俵の数を\(\,m\,\)（\(\,m\,≧\,4\,\)）とすると、
　\(\begin{eqnarray}\displaystyle
\frac{(m+4)(m-4+1)}{2}&=&60\\
(m+4)(m-3)&=&120\\
m^2+m-12&=&120\\
m^2+m-132&=&0\\
(m-11)(m+12)&=&0\\
m&=&11\,,\,-12
\end{eqnarray}\)

よって、\(\,m\,≧\,4\,\)なので
　\(\hspace{4pt}m=11\)

答え　\(\,\underline{　11　個}\,\)

文字は何でも良いです。
さらに\(\,m\,\)についての条件は\(\,m\,＞\,0\,\)でも減点はされないでしょう。
※
問題には「上」、「下」と書き分けられているので、
「下」が「上」より少ないことはありません。
段数が\(\,1\,\)のとき等号が成り立ちます。

問３

\(\,1\,\)次関数のグラフの読み取りと利用問題です。

\(\,\mathrm{A}\,\)店と\(\,\mathrm{B}\,\)店で販売価格が違います。

\(\,\mathrm{A}\,\)店
　\(\,\mathrm{1\,cm}\,\)当たり\(\,5円\,\)

\(\,\mathrm{B}\,\)店
　\(\,\mathrm{70cmま}\,\)では定額で\(\,250\,\)円
　\(\,\mathrm{70\,cm}\,\)を超えると\(\,\mathrm{1\,cm}\,\)当たり\(\,6\,\)円

長さを\(\,x\,\)、代金を\(\,y\,\)としてこの販売価格は価数で表せますが、
後に問題として出てきますので問題の指示通りに進めます。

\(\,\mathrm{Ⅰ}\,\)

(1)
\(\,\mathrm{A}\,\)店と\(\,\mathrm{B}\,\)店で代金が等しくなる点をグラフから探します。

代金が等しくなるのは\(\,y\,\)座標が同じになるときです。
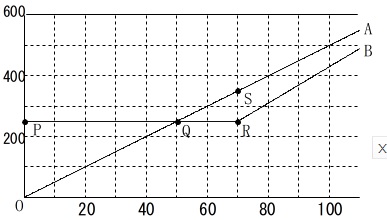点\(\,\mathrm{Q}\,\)です。

答え　\(\,\underline{　イ　}\,\)

(2)
\(\,\mathrm{30\,cm}\,\)買うときどちらがいくら安いか求めます。

\(\,\mathrm{30\,cm}\,\)買うとき
　\(\,\mathrm{A}\,\)店：\(\,5\times 30=150　円\,\)
　\(\,\mathrm{B}\,\)店：定額の\(\,250　円\,\)

代金は\(\,\mathrm{A}\,\)店の方が安く、
差は
　\(\,250-150=100　円\,\)

答え　\(\,\mathrm{\underline{　A　}店}\,\)　差額　\(\,\underline{　100　}円\,\)

(3)
\(\,\mathrm{A}\,\)店と\(\,\mathrm{B}\,\)店の代金を関数にします。

長さを\(\,x\,\mathrm{cm}\,\)とするときの代金\(\,y\,\)は
\(\,\mathrm{A}\,\)店:
　\(\hspace{10pt}\,y=5x\,\)

\(\,\mathrm{B}\,\)店では
\(\,\mathrm{70\,cm}\,\)までは定額なので
　\(\hspace{4pt}y=250\,(\,0\,＜\,x\,≦\,70\,)\)
後は
　\(\,(\,70\,,\,250\,)\,\)
を通り傾き\(\,6\,\)の直線になるので
　\(\hspace{4pt}y=6x-170　(\,70\,＜\,x\,)\)

答え　\(\color{black}{\fbox{　あ　}}\)　\(\,\underline{　6　}\,\)
　
(4)
\(\,\mathrm{50\,cm}\,\)より長いリボンを安く買える店がどちらか求めます。

グラフを読み取れば分かりますが、
\(\,\mathrm{50\,cm}\,\)より長いときは関数が再び交わるとき同じ代金になり、
それより長いと\(\,\mathrm{A}\,\)店の方がグラフが下になるので安くなります。

①
\(\color{black}{\fbox{　い　}}\)には\(\,x\,＞\,50\,\)での交点の\(\,x\,\)座標が入るので、
2つのグラフの交点を求めます。

グラフの交点を求めるのは連立方程式です。

連立すると
　\( \begin{cases}
\hspace{4pt} y=5x\\
\hspace{4pt} y=6x-170
\end{cases}\)

これを解くと
　\(\,x=170\,,\,y=850\,\)

②

答え　\(\color{black}{\fbox{　い　}}\)　\(\,\underline{　170　}\,\)

\(\,\mathrm{Ⅱ}\,\)

\(\,\mathrm{A}\,\)店が値段の設定を変えます。

(1)
〔企画案\(\,1\,\)〕
　\(\,\mathrm{50\,cm}\,\)より長い値段を変える。
　\(\,\mathrm{100\,cm}\,\)より長いリボンを\(\,\mathrm{B}\,\)店より安くする。

グラフが与えられていてややこしい説明がありますが、

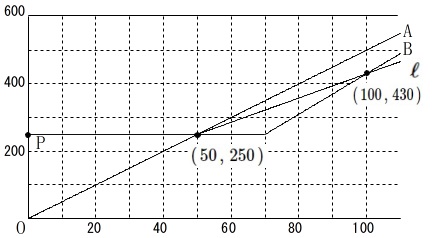
\(\,\mathrm{B}\,\)店の価格の関数は
　\(\hspace{4pt}y=6x-170\)
なので\(\,x=100\,\)のときの\(\,y=430\,\)だから、
\(\,\mathrm{A}\,\)店の値段を関数としてみると
　\(\,(\,50\,,\,250\,)\,\)
　\(\,(\,100\,,\,430\,)\,\)
の\(\,2\,\)点を通る直線が\(\,\ell\,\)です。

この\(\,\ell\,\)を表す関数は
　\(\hspace{10pt}\displaystyle y=\frac{18}{5}\,x+70\)

つまり傾きは\(\displaystyle \,\frac{18}{5}\,\)です。

答え　\(\color{black}{\fbox{　う　}}\)　\(\displaystyle \underline{　\frac{18}{5}　}\)

傾きは\(\,\mathrm{1\,cm}\,\)当たりの価格を表すので
\(\,\mathrm{B}\,\)店より安くするには\(\,\mathrm{1\,cm}\,\)当たり
　\(\displaystyle \,\frac{18}{5}=3.6\,\)
より小さい整数で最も大きい\(\,\underline{　3　}\,\)円にする、という企画です。
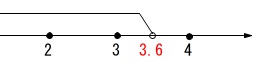ある値より小さい整数はいくらでもありますが、
その中でも最大の整数を考えるときは数直線は書いた方が良いです。

(2)
企画\(\,2\,\)があります。

\(\,\mathrm{B}\,\)店と同じようにある長さまでは一定の価格にし、
それより長い場合は\(\,\mathrm{1\,cm}\,\)当たりの価格を決めて加える、
という価格設定です。

〔企画案\(\,2\,\)〕
　ある長さまで\(\,200\,\)円の定額にする。
　ある長さをこえた分は\(\,\mathrm{1\,cm}\,\)当たり\(\,5\,\)円。
　\(\,\mathrm{100\,cm}\,\)のとき\(\,\mathrm{B}\,\)店と同じ値段と等しくなるようにする。

この企画の\(\,\mathrm{A}\,\)店の価格を関数で表すと、
　ある長さまでは\(\,y=200\,\)
　ある長さをこえたら\(\,y=5x+b\,\)

\(\,\mathrm{100\,cm}\,\)のとき\(\,\mathrm{B}\,\)店では\(\,y=6x-170\,\)なので
　\(\,(\,100\,,\,430\,)\,\)
\(\,y=5x+b\,\)はこの点を通ります。
このとき、
　\(\begin{eqnarray}\displaystyle
430&=&5\times (100)+b\\
b&=&-70
\end{eqnarray}\)
なので
　\(\hspace{10pt}y=5x-70\)

\(\,y=200\,\)とつながるのは、
　\(\begin{eqnarray}\displaystyle
200&=&5x-70\\
270&=&5x\\
x&=&\underline{　54　}
\end{eqnarray}\)

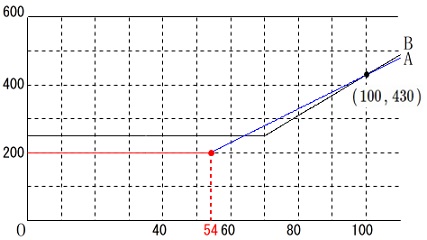
答え　\(\color{black}{\fbox{　お　}}\)　\(\,\underline{　54　}\,\)

関数だけで見れば難しい問題ではありませんが、
意味の読み取りができるかどうかがポイントですね。

問４

\(\,2\,\)点で交わる円の問題です。

条件
　\(\,2\,\)円の交点は\(\,\mathrm{A,B}\,\)
　\(\,\mathrm{PQ}\,\)は\(\,\mathrm{B}\,\)を通る。
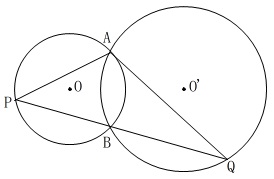問題が\(\,\mathrm{Ⅰ,Ⅱ}\,\)と分かれますが、
共通する条件はこれだけです。

\(\,\mathrm{Ⅰ}\,\)

\(\,\mathrm{P}\,\)を\(\,\mathrm{R}\,\)に動かしたときにともなって、
\(\,\mathrm{Q}\,\)が\(\,\mathrm{S}\,\)に動くとします。
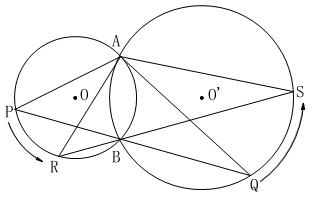ダラダラ説明しても意味ないので、
分かることを図に書き込んでおきます。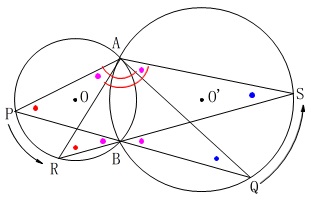円周角や対頂角が等しいことから等しい角が分かります。

(1)
\(\,\mathrm{∠PAQ=∠RSA}\,\)を証明します。

穴埋めなので円周角が等しいことと
\(\,\mathrm{∠RAQ}\,\)が共通であることをいえば終わります。

　\(\color{black}{\fbox{　あ　}}\)　\(\,\mathrm{\underline{　QS　}}\,\)
　\(\color{black}{\fbox{　い　}}\)　\(\,\mathrm{\underline{　∠RAQ　}}\,\)

(2)
また証明です。（しつこいな。）
\(\,\mathrm{△PAQ}\,\)∽\(\,\mathrm{△RAS}\,\)を証明し、
\(\,\mathrm{∠PAQ=∠QAS}\,\)を証明します。
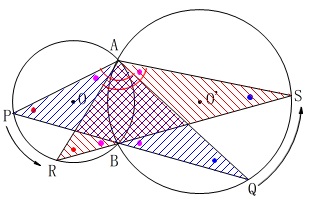\(\,2\,\)角相等条件から相似は明らかでしょう。

（証明）
　\(\,\mathrm{△PAQ}\,\)と\(\,\mathrm{△RAS}\,\)において
弧\(\,\mathrm{AB}\,\)の円周角が等しいことから
円\(\,\mathrm{O}\,\)において
　\(\mathrm{∠APQ=∠ARS}　･･･①\)
円\(\,\mathrm{O’}\,\)において
　\(\mathrm{∠AQP=∠ASR}　･･･②\)
①②より
　\(\,2\,\)組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△PAQ}\,\)∽\(\,\mathrm{△RAS}\,\)
相似な三角形の対応する角は等しいので、
　\(\,\mathrm{∠PAQ=∠RAS}\,\)
（終わり）

(3)
\(\,\mathrm{△PAQ}\,\)∽\(\,\mathrm{△RAS}\,\)であることから、
\(\,\mathrm{∠PAQ=∠RAS}\,\)の他に言えることを探します。

選択肢には角度ではなく辺の比だけがあるので、
辺の比で言えることを探せば良いだけです。
　\(\mathrm{PA:RA=AQ:AS=PQ:RS}\)
なので、正しいのは\(\,\mathrm{AP:AR=AQ:AS}\,\)です。

答え　\(\,\underline{　イ　}\,\)

\(\,\mathrm{Ⅰ}\,\)では相似な図形の基本性質しか聞かれていません。

\(\,\mathrm{Ⅱ}\,\)

長さの条件が加わります。

条件
　\(\,\mathrm{AB=BP=PA=BQ=4}\,\)
（単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）
ほとんどのことが分かりますが、
問題の順に解いていきましょう。

(1)
\(\,\mathrm{∠BAQ}\,\)の大きさを求めます。

\(\,\mathrm{△ABP}\,\)が正三角形なので、
　\(\,\mathrm{∠ABQ=120^{\circ}}\,\)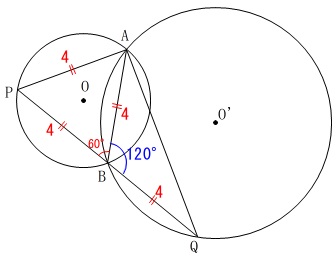\(\,\mathrm{△BAQ}\,\)は二等辺三角形なので、
底角が等しくなることから
　\(\begin{eqnarray}\displaystyle
\mathrm{∠BAQ}&=&\frac{180^{\circ}-120^{\circ}}{2}\\
&=&\underline{　30^{\circ}　}
\end{eqnarray}\)

(2)
円\(\,\mathrm{O}\,\)の半径を求めます。
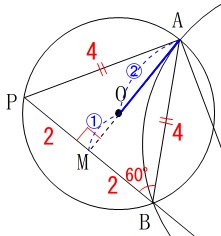\(\,\mathrm{△ABP}\,\)は正三角形なので、
\(\,\mathrm{A}\,\)から\(\,\mathrm{PB}\,\)に垂線を引くと円の中心\(\,\mathrm{O}\,\)を通ります。

このとき\(\,\mathrm{O}\,\)は\(\,\mathrm{△ABP}\,\)の重心になるので、
　\(\,\mathrm{AO:OM=\color{blue}{2}:\color{blue}{1}}\,\)

\(\,\mathrm{△APM}\,\)は三角定規で
　\(\begin{eqnarray}\displaystyle
\mathrm{PM:AM}&=&1:\sqrt{3}\\
2:\mathrm{AM}&=&1:\sqrt{3}\\
\mathrm{AM}&=&2\sqrt{3}
\end{eqnarray}\)

よって、円\(\,\mathrm{O}\,\)の半径となる\(\,\mathrm{AO}\,\)は
　\(\begin{eqnarray}\displaystyle
\mathrm{AO}&=&\frac{\color{blue}{2}}{\color{blue}{2}+\color{blue}{1}}\times 2\sqrt{3}\\
&=&\underline{　\frac{4\sqrt{3}}{3}　\mathrm{cm}}
\end{eqnarray}\)

(3)
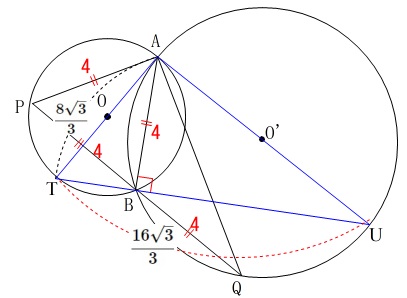
\(\,\mathrm{A,B}\,\)を通る条件は同じで\(\,\mathrm{△ATU}\,\)を作り、
\(\,\mathrm{△ATUの}\,\)面積が最大のときの面積を求めます。

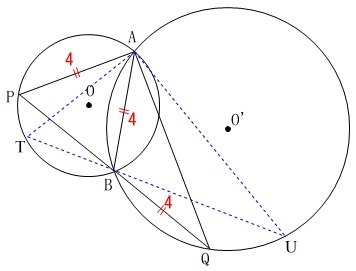
\(\,\mathrm{Ⅰ}\,\)でしつこいくらいに証明してきました。
　\(\,\mathrm{△APQ}\,\)∽\(\,\mathrm{△ATU}\,\)

\(\,\mathrm{△ATU}\,\)の面積が最大になるのは、
辺のどれかが最大になるときと考えて良いので、
\(\,\mathrm{AT}\,\)が最大のときを考えると、
\(\,\mathrm{AT}\,\)が円\(\,\mathrm{O}\,\)の直径と一致するときです。
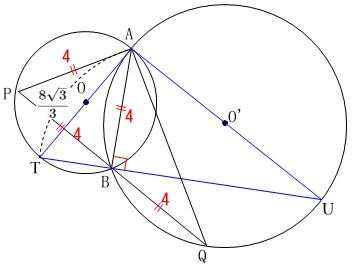\(\,\mathrm{AT}\,\)が直径になるとき(2)で半径を求めているので
　\(\mathrm{AT}=\displaystyle \frac{8\sqrt{3}}{3}\)

また直径に対する円周角が\(\,90^{\circ}\,\)になるので、
\(\,\mathrm{△ATU}\,\)の底辺は\(\,\mathrm{TU}\,\)、
高さを\(\,\mathrm{AB}\,\)と見ることができます。

　\(\,\mathrm{△APQ}\,\)∽\(\,\mathrm{△ATU}\,\)

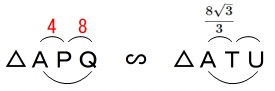
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AP:AT}&=&\mathrm{PQ:TU}\\
4:8&=&\frac{8\sqrt{3}}{3}:\mathrm{TU}\\
4\times \mathrm{TU}&=&\frac{64\sqrt{3}}{3}\\
\mathrm{TU}&=&\frac{16\sqrt{3}}{3}
\end{eqnarray}\)

よって、求める\(\,\mathrm{△ATU}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ATU}&=&\frac{1}{2}\times \mathrm{TU}\times \mathrm{AB}\\
&=&\frac{1}{2}\times \frac{16\sqrt{3}}{3}\times 4\\
&=&\underline{　\frac{32\sqrt{3}}{3}　\mathrm{cm^2}}
\end{eqnarray}\)

または
　\(\,\mathrm{△ATB}\,\)∽\(\,\mathrm{△UAB}\,\)∽\(\,\mathrm{△UTA}\,\)
で三角定規の比を持つ三角形だと気がつけば、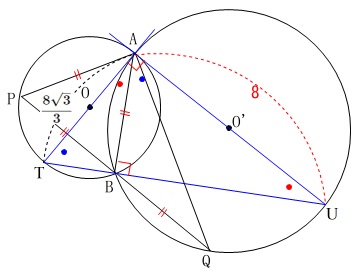
円\(\,\mathrm{O’}\,\)の直径が底辺で
　\(\,\mathrm{AU=8}\,\)
高さが\(\,\mathrm{AT}\,\)になるので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ATU}&=&\frac{1}{2}\times \mathrm{AU}\times \mathrm{AT}\\
&=&\frac{1}{2}\times 8\times \frac{8\sqrt{3}}{3}\\
&=&\underline{　\frac{32\sqrt{3}}{3}　\mathrm{cm^2}}
\end{eqnarray}\)
でも良いですよ。

(4)
(3)で求めた\(\,\mathrm{△ATU}\,\)の面積が\(\,\mathrm{△APQ}\,\)の面積の何倍か求めます。

\(\,\mathrm{△ATU}\,\)と\(\,\mathrm{△APQ}\,\)が相似なので、
相似比が
　\(\hspace{4pt}\displaystyle \mathrm{AT}:\mathrm{AP}=\frac{8\sqrt{3}}{3}:4\)
なので面積比は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ATU:△APQ}&=&\left(\frac{8\sqrt{3}}{3}\right)^2:4^2\\
&=&\frac{64\times 3}{9}:16\\
&=&\frac{64}{3}:16\\
&=&64:48\\
&=&4:3
\end{eqnarray}\)

よって、
　\(\hspace{4pt}\displaystyle \mathrm{△ATU}=\frac{4}{3}\times \mathrm{△APQ}\)

答え　\(\displaystyle \underline{　\frac{4}{3}　倍}\)

\(\,\mathrm{△APQ}\,\)は、
　底辺が\(\,\color{red}{8}\,\)
　高さが\(\,\color{blue}{2\sqrt{3}}\,\)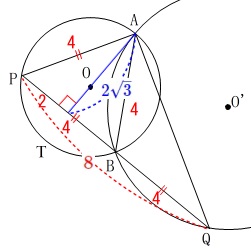なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\frac{1}{2}\times 8\times 2\sqrt{3}\\
&=&8\sqrt{3}
\end{eqnarray}\)

よって、
　\(\hspace{10pt}\displaystyle \frac{32\sqrt{3}}{3}\div 8\sqrt{3}\\
=\displaystyle \frac{32\sqrt{3}}{3}\times \frac{1}{8\sqrt{3}}\\
\displaystyle =\underline{　\frac{4}{3}　倍}\)

でも良いです。
応用が厳しい問題ではないので思いついた方針でどんどん進めれば良いです。

以上です。

⇒　長野県公立高校入試数学の問題と解説

対策は別として、数年分見ておけば傾向は見えてきます。
取り組みにくく感じるかもしれませんが基本中心の問題が多いです。