2019年(平成31年)度滋賀県公立高校入試の数学第3問の解説

2019年（平成31年）度に滋賀県で行われた公立高校入試の数学、第3問の解説です。
紙コップを回転させるときの回転数と中心角の関係や相似を利用した長さの関係式を求める問題で、平面図形と比例反比例の融合となっていますが、変化する値と変化しない値を見分けられれば関係式が立てられます。
この問題は手を動かすか動かないかで大きな差の出る問題ですよ。

問題は滋賀県が公開してくれています。

⇒　2019年滋賀県公立高校入試数学問題

円周の分割と中心角と相似

\(\color{black}{\fbox{　3　}}\)は紙コップをすべらないように回転させたときの、線分の長さと回転数の関係です。

図が\(\,1\,\)～\(\,3\,\)まであり、表もあるので読み取りにくいかもしれませんが、変わらないものと変わるものを理解すれば難しくはありません。

紙コップが円錐台になっているので転がすと回転しますが、
\(\,\mathrm{AB}\,\)と\(\,\mathrm{DC}\,\)とを延長した交点が回転の中心で、
変化しないのは\(\,\mathrm{AD}\,\)と\(\,\mathrm{BC}\,\)です。
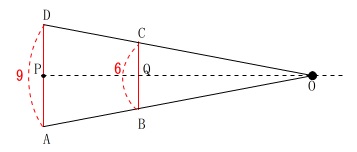これが理解できれば表の関係はすべてはっきりしますが、
一度に解決する必要はないので後は問題に合わせて見ていきましょう。

相似を利用した回転半径

コップ③は\(\,\mathrm{AB=16.5}\,\)です。
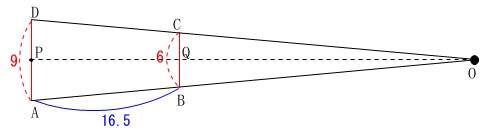ここで
　\(\,\mathrm{△OBC}\,\)　∽　\(\,\mathrm{△OAD}\,\)
なので
　\(\begin{eqnarray}
\mathrm{BC:AD}&=&\mathrm{OB:OA}\\
6:9&=&2:3
\end{eqnarray}\)
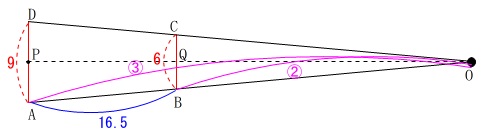このことから

　\(\,\mathrm{OA:BA=3:1}\,\)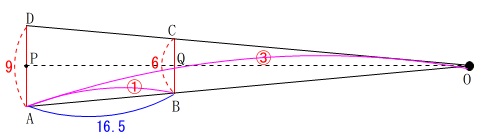よって、

　\(\begin{eqnarray}
\mathrm{OA:AB}&=&3:1\\
r:16.5&=&3:1\\
r&=&16.5\times 3\\
r&=&\underline{　49.5　}
\end{eqnarray}\)

単なる相似を利用した長さを求める問題でした。

回転数と反比例

(2)は\(\,\mathrm{AB}\,\)の長さの違いによる回転数の問題です。

\(\,\mathrm{AB}\,\)は長さが変わりますが、長くなると回転中心までの距離が長くなるので回転数は多くなります。
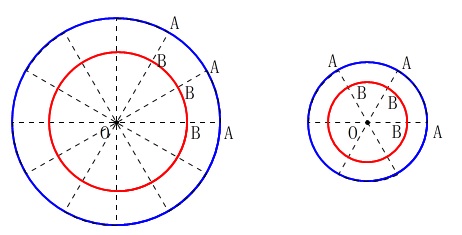このことと、回転数は中心角の\(\,360^{\circ}\,\)を等分すること
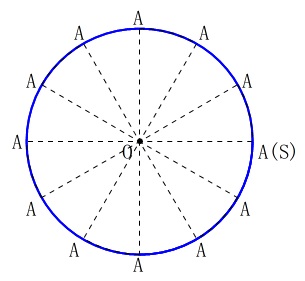それさえ分かれば、この問題は簡単です。

コップ②は\(\,9\,\)回転するので

　\(\begin{eqnarray}
∠\mathrm{AOS}&=&\frac{360^{\circ}}{9}\\
&=&\underline{　40^{\circ}}
\end{eqnarray}\)

表からコップが\(\,1\,\)回転させたときの\(\,\mathrm{∠AOS}\,\)と、
コップの回転数との関係を説明せよ、となっています。

回転数が多い方が中心角が小さくなることからも分かるように、

　\(\,\mathrm{∠AOS}\,\)と回転数\(\,m\,\)は反比例

します。

関係式は

　\(\,∠\mathrm{AOS}=y^{\circ}\,\)
　回転数を\(\,m\,\)

とすると、

　\(\displaystyle m=\frac{360}{y}\)
または
　\(\displaystyle y=\frac{360}{m}\)

となるので、

　コップが円を\(\,1\,\)周する回転数\(\,m\,\)が多くなったとき、
　\(\,\mathrm{∠AOS}\,\)は小さくなる。

　答え　\(\,\underline{　イ　}\,\)　

線分の関係と文字式の利用

(3)
コップの形は横から見ると台形です。
その長さを

　\(\,\mathrm{AD}=\color{red}{a}\,\)
　\(\,\mathrm{BC}=\color{blue}{b}\,\)
　\(\,\mathrm{AB}=\color{magenta}{x}\,\)

とし、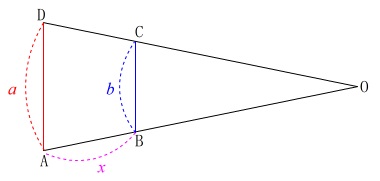　回転数を\(\,m\,\)

としたときの、

　\(\,\color{red}{a}\,,\,\color{blue}{b}\,,\,\color{magenta}{x}\,,\,m\,\)

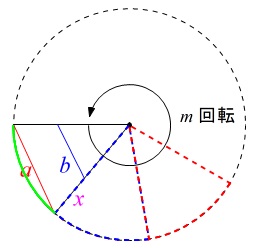
を関係式を表します。

少し数式の扱いに慣れていないと時間がかかるかもしれませんが、
　回転半径\(\,\mathrm{OA}\,\)の周を、
　コップが\(\,1\,\)回転するときの円周で割れば、
　回転数\(\,m\,\)
が出てきます。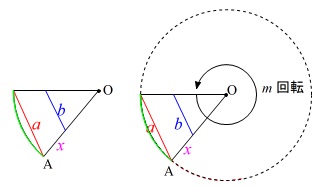

その前に、

　相似比は　\(\,\color{red}{a}:\color{blue}{b}=\mathrm{\color{red}{OA}:\color{blue}{OB}}\,\)

で回転半径の1つとして\(\,\mathrm{OB}\,\)が関係するので
\(\,\mathrm{OB}\,\)の長さを\(\,x\,\)で表しておきましょう。

\(\,\mathrm{OB}=y\,\)としておきます。

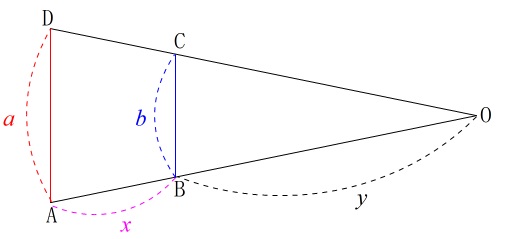
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{OA}:\color{blue}{OB}}&=&\mathrm{\color{red}{AD}:\color{blue}{BC}}\\
(\color{magenta}{x}+y):y&=&\color{red}{a}:\color{blue}{b}\\
\color{red}{a}y&=&\color{blue}{b}(\color{magenta}{x}+y)\\
ay&=&bx+by\\
ay-by&=&bx\\
(a-b)y&=&bx\\
\displaystyle y&=&\frac{\color{blue}{b}}{(\color{red}{a}-\color{blue}{b})}\color{magenta}{x}　･･･①
\end{eqnarray}\)

回転数\(\,m\,\)は、

　回転半径\(\,\mathrm{OA}\,\)の周をコップの直径\(\,\mathrm{AD}\,\)の周で割る。

または

　回転半径\(\,\mathrm{OB}\,\)の周をコップの直径\(\,\mathrm{BC}\,\)の周で割る。

と出てくるので、それを関係式にすれば良いのです。

回転半径\(\,\mathrm{OA}\,\)の周は\(\,x+y\,\)を出していないので、回転半径\(\,\mathrm{OB}\,\)からやります。
（回転半径\(\,\mathrm{OA}\,\)については後でやります。）

半径\(\,\mathrm{OB}=y\,\)の円周の長さは、

　\(\begin{eqnarray}
y&=&2\pi \times y\\
&=&2\,y\,\pi
\end{eqnarray}\)

\(\,\mathrm{BC}=\color{blue}{b}\,\)を直径とする円周の長さは\(\,\color{blue}{b}\,\pi\,\)なので

回転数\(\,m\,\)は

　\(\begin{eqnarray}\displaystyle
m&=&2\,y\,\pi\div \color{blue}{b}\,\pi\\
\displaystyle &=&\frac{2\,y\,\pi}{\color{blue}{b}\,\pi}\\
\displaystyle &=&\frac{2\,y}{\color{blue}{b}}　･･･②
\end{eqnarray}\)

ここで先ほど\(\,y\,\)は\(\,x\,\)で表しておいたので①を利用します。

　\(\displaystyle y=\frac{\color{blue}{b}}{(\color{red}{a}-\color{blue}{b})}\color{magenta}{x}\)

を②に代入して、

　\(\begin{eqnarray}\displaystyle
\displaystyle m&=&\frac{2\,y\,}{\color{blue}{b}}\\
\displaystyle &=&\frac{2}{\color{blue}{b}}\times y\\
\displaystyle &=&\frac{2}{\color{blue}{b}}\times \frac{\color{blue}{b}}{(\color{red}{a}-\color{blue}{b})}\color{magenta}{x}\\
\displaystyle &=&\frac{2x}{a-b}
\end{eqnarray}\)

よって、\(\,\mathrm{A},\mathrm{B},x,m\,\)の関係式は、

　\(\displaystyle \underline{　m=\frac{2x}{a-b}　}\)

となります。

これは変形すると、

　\(\begin{eqnarray}\displaystyle
m&=&\frac{2x}{a-b}\\
m(a-b)&=&2x\\
\end{eqnarray}\)

から

　\(\displaystyle \underline{　x=\frac{m(a-b)}{2}　}\)

とも表すことができます。
理由は上に書いたとおりです。

滋賀県の解答ではコップ\(\,1\,\)回転の周の長さに回転数をかけると回転半径の円周になることが利用され、
さらに\(\,\mathrm{OB}\,\)の長さが\(\,\mathrm{OA}\,\)から\(\,\mathrm{AB}\,\)を引いた長さであることから関係式を出しています。

どちらでも良いですよ。
関係式は変わりません。

ただ、回転半径\(\,\mathrm{OA,OB}\,\)の周の長さがコップ\(\,1\,\)回転の円周の長さに回転数\(\,m\,\)をかける方程式が立てられるなら上の解答は十分理解できるでしょう。
模範解答へのつなぎ役としてご利用ください。

回転半径\(\,\mathrm{OA}\,\)つまり半径が\(\,(x+y)\,\)を利用した場合の関係式も導いておきます。
もちろん結果は同じにならなければおかしいですよ。

①に戻って見てください。

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{OA}:\color{blue}{OB}}&=&\mathrm{\color{red}{AD}:\color{blue}{BC}}\\
(\color{magenta}{x}+y):y&=&\color{red}{a}:\color{blue}{b}\\
\color{red}{a}y&=&\color{blue}{b}(\color{magenta}{x}+y)　･･･③\\
ay&=&bx+by\\
ay-by&=&bx\\
(a-b)y&=&bx\\
\displaystyle y&=&\frac{\color{blue}{b}}{(\color{red}{a}-\color{blue}{b})}\color{magenta}{x}　･･･①
\end{eqnarray}\)

③の式から

　\(\begin{eqnarray}\displaystyle
a\,y&=&b\,(x+y)\\
b\,(x+y)&=&a\,y\\
\displaystyle \color{red}{x+y}&=&\color{blue}{\frac{a\,y}{b}}　･･･④
\end{eqnarray}\)

このとき\(\,\mathrm{OA}\,\)を回転半径とする円周は、

　\(\begin{eqnarray}\displaystyle
2\,\pi\,(\color{red}{x+y})&=&2\,\pi\times\color{blue}{\frac{a\,y}{b}}\\
&=&\color{magenta}{\frac{2\,a\,y\,\pi}{b}}
\end{eqnarray}\)

これを直径\(\,a\,\)の円周\(\,a\,\pi\,\)で割ると回転数\(\,m\,\)が出てきます。

　\(\begin{eqnarray}\displaystyle
\displaystyle m&=&\color{magenta}{\frac{2\,a\,y\,\pi}{b}}\div {a\,\pi}\\
&=&\color{magenta}{\frac{2\,a\,y\,\pi}{b}}\times \frac{1}{a\,\pi}\\
&=&\frac{2\,y}{b}
\end{eqnarray}\)

これに①を代入すると先ほどと同じになるはずです。

　\(\begin{eqnarray}\displaystyle
m&=&\frac{2\,\color{red}{y}}{b}\\
&=&\frac{2}{b}\times \color{red}{\frac{b\,x}{a-b}}\\
&=&\frac{2\,x}{a-b}
\end{eqnarray}\)

または、

　\(\begin{eqnarray}\displaystyle
m&=&\frac{2\,x}{a-b}\\
m\,(a-b)&=&2\,x\\
x&=&\frac{m\,(a-b)}{2}
\end{eqnarray}\)

いずれにしても関係式は、

　\(\underline{　2\,x=m\,(a-b)　}\)

これは「\(\,m\,\)を」や「\(\,x\,\)を」表せという指定がないので分数でなくても関係式は同じです。

\(\color{black}{\fbox{　3　}}\)は以上です。

⇒　2019年(平成31年)度滋賀県公立高校入試の数学第4問の解説

\(\color{black}{\fbox{　4　}}\)は平面図形の総合問題ですが、正多角形なのであつかいやすいです。

⇒　滋賀県公立高校入試2019年数学問題の解説

\(\color{black}{\fbox{　1　}}\)は小問集合で配点が\(\,43\,\)点、

⇒　滋賀県公立高校入試2019年数学データの活用問題の解説

\(\color{black}{\fbox{　2　}}\)はデータの活用で配点が\(\,17\,\)点あり、
\(\color{black}{\fbox{　1　}}\)、\(\color{black}{\fbox{　2　}}\)だけで\(\,60\,\)点分あることは確認しておきましょう。