2019年(平成31年)度滋賀県公立高校入試の数学第4問の解説

2019年（平成31年）度に滋賀県で行われた公立高校入試の数学、第4問の解説です。
第4問は正方形と正三角形との重なり、正六角形と正三角形の重なりについての図形総合問題です。
最後の面積を求める問題まで落ち着いて問題を見れば、対称性からそれほど難しい問題ではありませんので簡単に済ませます。

問題は滋賀県が公開してくれています。

⇒　2019年滋賀県公立高校入試数学問題

正方形と正三角形

(1)正方形の1つの頂点に、正三角形の1つの頂点が対称に重なっています。
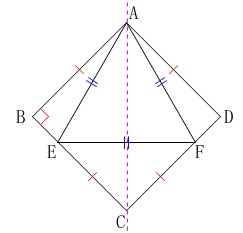分かっているのは正三角形の\(\,1\,\)辺です。

　\(\,\mathrm{AE=EF=AF}=\sqrt{2}\,\)

すべての長さは求めることができますが、問題はそこまで聞いていません。

正方形の\(\,1\,\)辺を\(\,\color{red}{x}\,\)とすると\(\,\mathrm{BE}\,\)の長さは\(\,\color{red}{x}\,\)用いて表すとどうなるか？
それだけです。
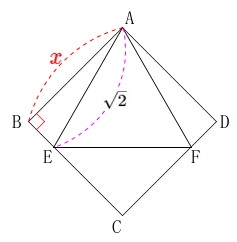\(\,\mathrm{△ABE}\,\)は直角三角形なので三平方の定理が使えます。

　\(\begin{eqnarray}
\mathrm{AB^2+BE^2}&=&\mathrm{AE^2}\\
x^2+\mathrm{BE^2}&=&(\sqrt{2})^2\\
\mathrm{BE^2}&=&(\sqrt{2})^2-x^2\\
\mathrm{BE}&=&\pm \sqrt{2-x^2}
\end{eqnarray}\)

\(\,\mathrm{BE}\,\)は長さなので正の平方根をとって、

　\(\mathrm{BE}=\underline{　\sqrt{2-x^2}　}\)

また、\(\,\mathrm{AC}\,\)と\(\,\mathrm{EF}\,\)の交点を\(\,\mathrm{G}\,\)とすると、\(\,\mathrm{△AEG}\,\)は三角定規になるので、

　\(\displaystyle \mathrm{EG}=\color{blue}{\frac{\sqrt{2}}{2}}\)

で、\(\,\mathrm{△CEG}\,\)は直角二等辺三角形になるので

　\(\mathrm{CE}＝1\)

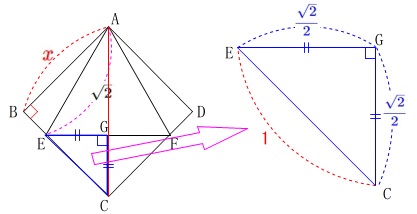
よって

　\(\begin{eqnarray}
\mathrm{BE}&=&\mathrm{BC-CE}\\
&=&\underline{　x-1　}
\end{eqnarray}\)

と表すこともできます。

これらの関係から

　\(\begin{eqnarray}
\sqrt{2-x^2}&=&x-1
\end{eqnarray}\)

の両辺を\(\,2\,\)乗することで具体的な長さも求まります。
求める必要はありませんが、長さなので正の数にならなければ不適です。

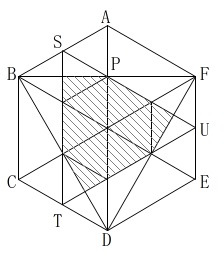
正六角形と正三角形

(2)
条件を図示しておきます。
対称性を見れば最後までさほど時間はかからないでしょう。

条件

　正六角形\(\,\mathrm{ABCDEF}\,\)の面積は\(\,40\sqrt{3}\,\)
　\(\,\mathrm{ＡＢ,ＣＤ,ＥＦ}\,\)の中点を\(\,\mathrm{S,T,U}\,\)
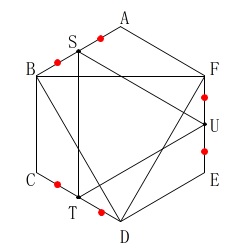もっと対称性の分かる条件を書き込むとすぐに終わる問題ですが、問題の順番に説明して行きます。

①
線分\(\,\mathrm{BF}\,\)と線分\(\,\mathrm{SU}\,\)の交点を\(\,\mathrm{P}\,\)とするとき、

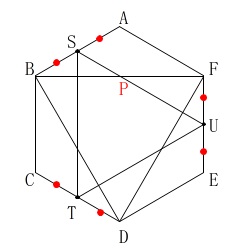
点\(\,\mathrm{P}\,\)が線分\(\,\mathrm{BF}\,\)の中点になっていることを証明します。

線分\(\,\mathrm{BE}\,\)を加えると分かり易いです。
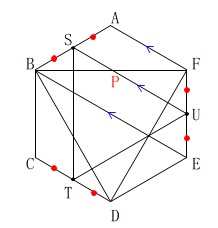点\(\,\mathrm{S,U}\,\)は線分\(\,\mathrm{AB,FE}\,\)の中点なので

　\(\mathrm{AF}\,/\!/\,\mathrm{SU}\,/\!/\,\mathrm{BE}\)

このとき

　\(\mathrm{AF}\,/\!/\,\mathrm{SP}\)

で、

　\(\,\mathrm{AS:SB=\color{red}{1:1}}\,\)
から
　\(\,\mathrm{FP:PB=\color{blue}{1:1}}\,\)
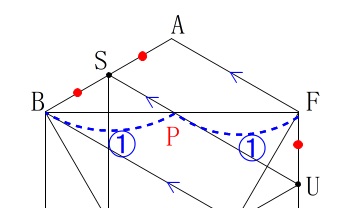なので中点連結定理により、
点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{BE}\,\)の中点になります。

証明は上で説明したこと表現してあれば良いですよ。

②
正六角形\(\,\mathrm{ABCDEF}\,\)の\(\,1\,\)辺の長さを求めます。

正六角形の面積は与えられているので、普通とは逆の問題になります。

正六角形は正三角形\(\,6\,\)個でできています。
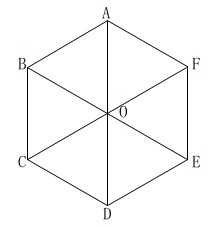\(\,\mathrm{AD,BE,CF}\,\)の交点を\(\,\mathrm{O}\,\)としておきます。

正三角形\(\,\mathrm{OAB}\,\)の面積は正六角形の\(\displaystyle \frac{1}{6}\)です。

　\(\begin{eqnarray}\displaystyle
△\mathrm{OAB}&=&\frac{1}{6}\times 40\sqrt{3}\\
&=&\color{magenta}{\frac{20\sqrt{3}}{3}}
\end{eqnarray}\)

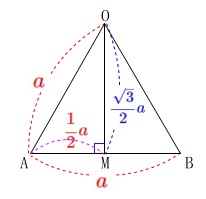
\(\,\mathrm{△OAB}\,\)の\(\,1\,\)辺を\(\,\color{red}{a}\,\)として方程式にしましょう。

正三角形の面積は求め慣れているでしょう。

\(\,\mathrm{O}\,\)から\(\,\mathrm{AB}\,\)の下ろした垂線と\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{M}\,\)とすると

　\(\displaystyle \mathrm{AM}=\color{red}{\frac{1}{2}a}\)
　\(\displaystyle \mathrm{OM}=\color{blue}{\frac{\sqrt{3}}{2}a}\)

の三角定規になるので

　\(\begin{eqnarray}\displaystyle
△\mathrm{OAB}&=&\frac{1}{2}\times \color{red}{a}\times \color{blue}{\frac{\sqrt{3}}{2}a}\\
\color{magenta}{\frac{20\sqrt{3}}{3}}&=&\frac{\sqrt{3}}{4}\,a^2\\
\frac{\sqrt{3}}{4}\,a^2&=&\frac{20\sqrt{3}}{3}\\
a^2&=&\frac{20\sqrt{3}}{3}\times \frac{4}{\sqrt{3}}\\
&=&\frac{80}{3}
\end{eqnarray}\)

\(\,a\,\)は長さなので正の平方根をとって、

　\(\begin{eqnarray}\displaystyle
a&=&\sqrt{\frac{80}{3}}\\
&=&\frac{\sqrt{80}}{\sqrt{3}}\\
&=&\frac{4\sqrt{5}}{\sqrt{3}}\\
&=&\underline{　\frac{4\sqrt{15}}{3}　}
\end{eqnarray}\)

正六角形\(\,\mathrm{ABCDEF}\,\)の\(\,1\,\)辺と、
正三角形\(\,\mathrm{OAB}\,\)の\(\,1\,\)辺は同じ長さ、

なのでこれが答えです。

もちろん、正三角形の面積を

　\(\displaystyle △\mathrm{OAB}=\frac{\sqrt{3}}{4}\,a^2\)

とした後、
この\(\,6\,\)個分が正六角形の面積\(\,40\sqrt{3}\,\)として、

　\(\displaystyle 6\times \frac{\sqrt{3}}{4}\,a^2=40\sqrt{3}\)

を解いても同じです。どちらでも良いですよ。

③
面積を求めますが、対称性を利用すれば線分の長さなどを求める必要が無いので簡単に出ます。
図の斜線部分ですが同じ大きさの部分が二通りあるだけです。
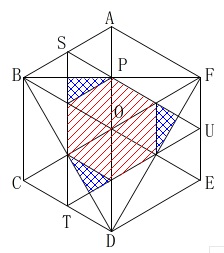図の赤い部分は正六角形で、正六角形\(\,\mathrm{ABCDEF}\,\)と相似比\(\,2：1\,\)なので、
面積は\(\,\mathrm{ABCDEF}\,\)の\(\displaystyle \,\frac{1}{4}\,\)で、

　\(\hspace{10pt}\displaystyle \frac{1}{4}\times 40\sqrt{3}\\
=\color{red}{10\sqrt{3}}\)

青い部分は正三角形\(\,\mathrm{OAB}\,\)の面積の\(\displaystyle \,\frac{1}{8}\,\)です。
それが3つ分あります。

正三角形\(\,\mathrm{OAB}\,\)の面積は正六角形の\(\displaystyle \,\frac{1}{6}\,\)なので

　\(\begin{eqnarray}\displaystyle
△\mathrm{OAB}&=&\frac{1}{6}\times 40\sqrt{3}\\
&=&\frac{20\sqrt{3}}{3}
\end{eqnarray}\)

青い部分は\(\,\mathrm{△OAB}\,\)の\(\displaystyle \,\frac{1}{8}\,\)で3つあるので

　\(\hspace{10pt}\displaystyle \frac{20\sqrt{3}}{3}\times \frac{1}{8}\times 3\\
\displaystyle =\color{blue}{\frac{5\sqrt{3}}{2}}\)

よって、求める面積は、

　\(\hspace{10pt}\displaystyle \color{red}{10\sqrt{3}}+\color{blue}{\frac{5\sqrt{3}}{2}}\\
\displaystyle =\underline{　\frac{25\sqrt{3}}{2}　}\)

青い部分一つが正三角形の\(\displaystyle \,\frac{1}{8}\,\)になることの説明です。

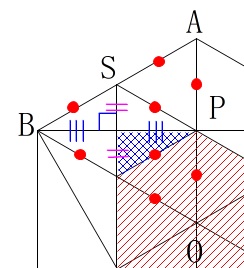\(\,\mathrm{△OAB}\,\)を詳しく見ると線分をすべての等分していることが分かります。

　\(\displaystyle \mathrm{\color{magenta}{△OBP}}=\frac{1}{2}\times \mathrm{\color{red}{△OAB}}\)

さらに、

　　\(\begin{eqnarray}\displaystyle
\displaystyle (\color{blue}{青い部分の面積})&=&\mathrm{\color{magenta}{△OBP}}\times \frac{1}{2}\times \frac{1}{2}\\
&=&\frac{1}{4}\,\times \mathrm{\color{magenta}{△OBP}}
\end{eqnarray}\)

なので、

　　\(\begin{eqnarray}\displaystyle
(\color{blue}{青い部分の面積})&=&\frac{1}{4}\times \frac{1}{2}\times \mathrm{\color{red}{△OAB}}\\
&=&\frac{1}{8}\times △\mathrm{OAB}
\end{eqnarray}\)

となります。

大ざっぱな説明になっていますが、この説明はあちこちでしているので全国の過去問を見ればどこにでもありますので確認しておいて下さい。

⇒　全国の公立高校入試 数学過去問の解答解説

滋賀県の\(\,2019\,\)年数学問題の解説は以上です。

⇒　滋賀県公立高校入試2019年数学問題の解説

\(\color{black}{\fbox{　1　}}\)から配点を見ながら全体をもう一度確認してみて下さい。

\(\color{black}{\fbox{　4　}}\)がそれほどやゆやこしくなかったので時間が余った人も多かったかもしれませんが、
時間が足りなかったという場合は時間配分を考えて取り組んでおきましょう。

⇒　滋賀県公立高校入試数学の問題と解説

例年、配点は均等になっているわけではありません。