2023年（令和5年度）大阪府公立高校入試数学C問題の解説

２０２３年（令和５年度）大阪府公立高校入試数学Ｃ問題の解説です。
Ｃ問題を受験する時点で基礎はできているという前提で解説します。
方針についてはできるだけ基本的なところからしますが、
公式は応用レベルのものも使うと思うのでご了承下さい。

2023年（令和5年度）大阪府公立高校入試数学のＣ問題

問題は大問３つです。
ページごとに分けておきました。

⇒　2023年（令和5年度）大阪府公立高校入試数学のＣ問題ＰＤＦ

大阪府公開分のＰＤＦも載せておきます。

⇒　令和５年度大阪府公立高校入試数学のＣ問題公開ＰＤＦ

自分で解く場合、
作業量からするとページごとの印刷を利用することをお勧めします。

2023年（令和5年度）大阪府公立高校入試数学C問題の解説

傾向や難易度は例年と変わりないので早速解説に入ります。
分かっていると思うのでしつこくはいいませんが、
作業は軽くないので覚悟はしておいて下さい。

第１問小問集合（総合分野）

\(\,\large{1}\,\)
(1)
　\(\hspace{10pt}\displaystyle -a\times (2ab)^2\div \left(-\frac{\color{blue}{2}}{\color{red}{3}}\color{blue}{ab^2}\right)\\
\displaystyle =\frac{a\times 4\,a^2\,b^2\times \color{red}{3}}{\color{blue}{2\,a\,b^2}}\\
\displaystyle =\underline{　6\,a^2　}\)

符号は良いとして、
逆数にする際分数の分母と分子をしっかり見て。
(2)
　\(\hspace{10pt}\displaystyle \color{red}{\frac{6+\sqrt{8}}{\sqrt{2}}}+(2-\sqrt{2})^2\\
\displaystyle =\color{red}{\frac{6\sqrt{2}+\sqrt{16}}{2}}+4-4\sqrt{2}+2\\
\displaystyle =\color{red}{3\sqrt{2}+2}+6-4\sqrt{2}\\
=\underline{　8-\sqrt{2}　}\)

過度な暗算はしていない、と思う。
（２行目はなくても良いかもしれないけど。）
(3)
方程式の解の基本です。
\(\hspace{10pt}\displaystyle ax^2+4x-7a-16=0\)

方程式に\(\,x=3\,\)を代入すると
　\(\begin{eqnarray}
9a+12-7a-16&=&0\\
2a&=&4\\
a&=&\underline{　2　}
\end{eqnarray}\)
この\(\,a\,\)を方程式に戻して解くと
　\(\begin{eqnarray}
2x^2+4x-30&=&0\\
x^2+2x-15&=&0\\
(x-3)(x+5)&=&0\\
x&=&3\,,\,-5
\end{eqnarray}\)
よってもう一つの解は
\(\hspace{10pt}x=\underline{　-5　}\)

解と係数の関係でも良いけどメンドウ。

⇒　方程式の解とは？2次方程式の係数と他の解を求める代入問題の解き方

方程式の解とは何かは説明の必要もないでしょうが一応確認して。
(4)
２つの関数の値域が一致する問題です。

定義域は\(\hspace{4pt}-3\,≦\,x\,≦\,1\,\)で、
関数\(\,\displaystyle y=a\,x^2\,\)と\(\,y=b\,x+1\,\)の値域が同じなので
\(\hspace{10pt}\color{red}{9a}=\color{blue}{-3b+1}\)（最大値が同じ。）
\(\hspace{10pt}\color{blue}{b+1}=\color{red}{0}\)（最小値が同じ。）
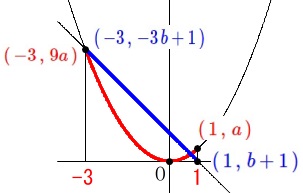最小値から\(\,b\,\)から求まりますね。
\(\hspace{10pt}\displaystyle b=\underline{　-1　}\,,\,a=\underline{\underline{　\frac{4}{9}　}}\)

放物線の\(\,(\,1\,,\,a\,)\,\)が最小値に関係ないことが分かればそれで良い。
(5)
連続自然数の個数を差で求めるときの注意が１つありますね。
\(\hspace{10pt}n\,≦\,\sqrt{x}\,≦\,n+1\)

全辺正の数だから平方しても成り立つので
\(\hspace{10pt}n^2\,≦\,x\,≦\,(n+1)^2\)
自然数\(\,x\,\)が\(\,100\,\)個あるので
　\(\begin{eqnarray}
(n+1)^2-n^2\color{red}{+1}&=&100\\
2n+2&=&100\\
n&=&\underline{　49　}
\end{eqnarray}\)

差は間隔なので\(\,\color{red}{+1}\,\)するのを忘れないように。
といっても忘れていれば答えに違和感を感じて思い出すだろうけど。
(6)
得点が偶数になる確率です。
得点の『きまり』
\(\hspace{10pt}\color{red}{a}\,,\,\color{blue}{b},\)の最大公約数が\(\,1\,\)のとき\(\,\color{red}{a}+\color{blue}{b}\,\)
\(\hspace{10pt}\color{red}{a}\,,\,\color{blue}{b},\)の最大公約数が\(\,1\,\)以外のとき\(\,\sqrt{2\,\color{red}{a}\,\color{blue}{b}}\,\)
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4}\, \\ \hline
\,\color{blue}{4}\, & 5 & \color{magenta}{4} & 7 & \sqrt{32}\\ \hline
\color{blue}{5} & \color{magenta}{6} & 7 & \color{magenta}{8} & 9\\ \hline
\color{blue}{6} & 7 & \sqrt{24} & \color{magenta}{6} & \sqrt{48}\\ \hline
\color{blue}{7} & \color{magenta}{8} & 9 & \color{magenta}{10} & 11\\ \hline
\color{blue}{8} & 9 & \sqrt{32} & 11 & \color{magenta}{8}\\ \hline
\end{array}\)
（計算しなくても明らかなところは省ける。）
答え\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{7}{20}　}}\)

全部でたかだか\(\,20\,\)通りなので、
樹形図書いて計算したら終わり。
（互いに素で和？と考えるくらいなら計算した方が早い。）
(7)
２つの自然数を\(\,x\,,\,y\,\)を使って表します。
\(\hspace{10pt}a=10x+y　･･･①\)
\(\hspace{10pt}b=10y+x　･･･②\)
条件を満たすとき
　\(\begin{eqnarray}
\frac{b^2-a^2}{99}&=&24\\
(\color{red}{b+a})(\color{blue}{b-a})&=&99\times 24\\
\end{eqnarray}\)
①②から
\(\hspace{10pt}\color{red}{b+a}=11x+11y=11(x+y)\)
\(\hspace{10pt}\color{blue}{b-a}=9y-9x=9(y-x)\)
これらから
　\(\begin{eqnarray}
(b+a)(b-a)&=&99\times 24\\
99(y+x)(y-x)&=&99\times 24\\
(y+x)(y-x)&=&24
\end{eqnarray}\)

左辺の２つの因数は整数（自然数）だから\(\,24\,\)の約数なので
\(\hspace{4pt}1\times 24\,,\,2\times 12\,,\,3\times 8\,,\,4\times 6\)
の中に\(\,y+x\,,\,y-x\,\)の組はあり、
\(\hspace{10pt}(y+x)+(y-x)=2y\)
だから因数の和が奇数になる組み合わせはあり得ない。

自然数だから\(\,y+x\,＞\,y-x\,\)であることも加えて
　\( \begin{cases}
\hspace{4pt} y+x=12\\
\hspace{4pt} y-x=2
\end{cases}\)
から\(\hspace{4pt}x=5\,,\,y=7\)
　\( \begin{cases}
\hspace{4pt} y+x=6\\
\hspace{4pt} y-x=4
\end{cases}\)
から\(\hspace{4pt}x=1\,,\,y=5\)

答え\(\hspace{4pt}a=\underline{　15　}\,,\,\underline{　57　}\)

因数の候補は全て計算しようとしたらすぐに気がつきます。
(8)
関数だけど文字設定すれば単なる方程式です。
（もちろん、グラフ上で座標を書き込む作業くらいはしましょう。）
条件から、
\(\hspace{4pt}\mathrm{A}\,\color{blue}{(\,5\,,\,5\,)}\,,\,\mathrm{B}\,(\,0\,,\,-1\,)\)
\(\hspace{4pt}\displaystyle \ell\,:\,y=\frac{6}{5}x-1\)
\(\hspace{4pt}\displaystyle \mathrm{C}\,\color{red}{\left(\,t\,,\,\frac{6}{5}\,t-1\,\right)}\,,\, \mathrm{D}\,\color{red}{\left(\,t\,,\,\frac{1}{5}\,t^2\,\right)}\,,\,\mathrm{E}\,\color{blue}{(\,t\,,\,5\,)}\)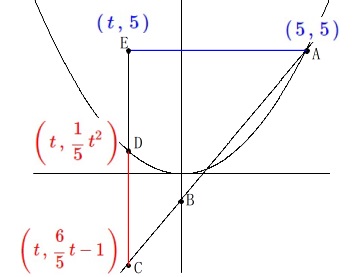よって、線分\(\,\mathrm{\color{red}{DC}}\,\)が線分\(\,\mathrm{\color{blue}{EA}}\,\)より\(\,\color{magenta}{3}\,\)短いから
　\(\begin{eqnarray}
\mathrm{\color{red}{DC}}&=&\mathrm{\color{blue}{EA}}\color{magenta}{-3}\\
\color{red}{\frac{1}{5}\,t^2}-\left(\,\color{red}{\frac{6}{5}\,t-1}\,\right)&=&\color{blue}{5}-\color{blue}{t}\color{magenta}{-3}\\
\frac{1}{5}\,t^2-\frac{6}{5}\,t+1&=&2-t\\
\frac{1}{5}\,t^2-\frac{1}{5}\,t-1&=&0\\
t^2-t-5&=&0\\
t&=&\frac{1\pm \sqrt{21}}{2}
\end{eqnarray}\)
\(\,t\,＜\,0\,\)なので
\(\hspace{4pt}\displaystyle t=\underline{\underline{　\frac{1-\sqrt{21}}{2}　}}\)

※長さの単位は\(\,\mathrm{cm}\,\)ですが関係式には関係ありません。

第２問平面図形（証明と長さ）

\(\,\large{2}\,\)
ひし形の条件を使い切れば、問題に十分な条件が与えられています。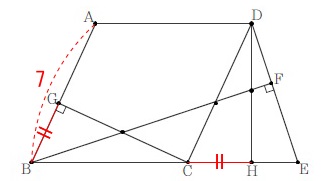四角形\(\,\mathrm{ABCD}\,\)はひし形です。
(1)
①
対角線\(\,\mathrm{AC}\,\)が\(\,a\,\)のとき四角形\(\,\mathrm{ABCD}\,\)の面積が\(\,S\,\)なので、
　\(\begin{eqnarray}
S&=&\frac{1}{2}\times a\times \mathrm{BD}\\
2S&=&a\times \mathrm{BD}\\
\mathrm{BD}&=&\underline{\underline{　\frac{2S}{a}　}}\mathrm{cm}
\end{eqnarray}\)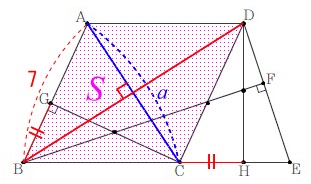公式としても良いですが、
ひし形は対角線が直交するので問題ないでしょう。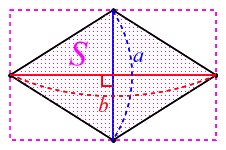ひし形の面積は対角線の積の半分です。
　\(\begin{eqnarray}
\color{magenta}{S}&=&\frac{1}{2}\times \color{blue}{a}\times \color{red}{b}
\end{eqnarray}\)
②
相似の証明です。
\(\hspace{10pt}\mathrm{△DHE}\,\)∽\(\,\mathrm{△BFE}\,\)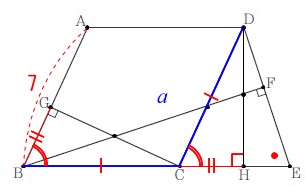薄々気がついていたと思いますが、
ひし形の１辺と平行線の同位角が等しいことから
「２組の辺とその間の角がそれぞれ等しい。」（合同条件）
\(\hspace{10pt}\mathrm{△CGB}\,\)≡\(\,\mathrm{△DCH}\,\)
なので\(\,\mathrm{∠DHE}=\mathrm{∠BFE}=90°\)
また、
\(\,\mathrm{△DHE}\,\)と\(\,\mathrm{△BFEは}\,\)
\(\hspace{10pt}\mathrm{\color{red}{∠DEH}}=\mathrm{\color{red}{∠BEF}}\)を共通にしているので
「２組の角がそれぞれ等しい。」（相似条件）

後は証明のルール通りにまとめれば良いだけです。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

この問題は相似の証明ですが合同の証明もあるので、
両方の成立条件は示すことがポイントになります。

ここまでの内容は問題\(\,\large{2}\,\)全体に通じていることを忘れずに。
(2)
条件が加わります。
\(\hspace{10pt}\mathrm{GB}=2\,,\,\mathrm{HE}=3\)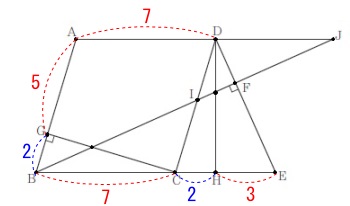①
線分\(\,\mathrm{FE}\,\)の長さですが、
(1)で証明した相似にあります。
\(\hspace{10pt}\mathrm{△DHE}\,\)∽\(\,\mathrm{△BFE}\,\)
ただ、\(\,\mathrm{△DHE}\,\)側の長さが足りていません。
証明の中で出てきた合同を使います。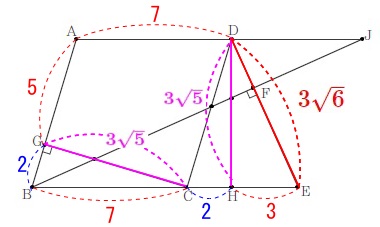三平方の定理から（計算は自分で。）
\(\hspace{10pt}\displaystyle \mathrm{CG=DH}=\color{magenta}{3\sqrt{5}}\)
さらに、\(\,\mathrm{△DHE}\,\)に三平方の定理を使って
\(\hspace{10pt}\displaystyle \mathrm{DE}=\sqrt{(\,\color{magenta}{3\sqrt{5}}\,)^2+3^2}=\color{red}{3\sqrt{6}}\)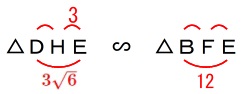\(\hspace{4pt}\mathrm{△DHE}\,\)∽\(\,\mathrm{△BFE}\,\)から
　\(\begin{eqnarray}
3:\mathrm{FE}&=&3\sqrt{6}:12\\
3\sqrt{6}\times \mathrm{FE}&=&3\times 12\\
\mathrm{FE}&=&\frac{12}{\sqrt{6}}\\
&=&\underline{　2\sqrt{6}　}\mathrm{cm}
\end{eqnarray}\)
②
線分\(\,\mathrm{IJ}\,\)を求めます。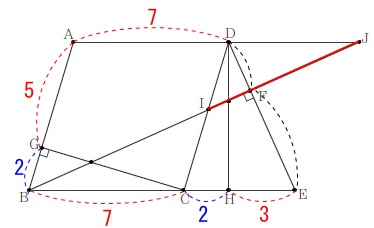相似がたくさんあるのでいろいろと方針は出てきたそうですが、
先ずは①で求めた長さを利用することを考えます。
\(\hspace{10pt}\displaystyle \mathrm{FE}=\color{red}{2\sqrt{6}}\,,\,\mathrm{DF}=\color{blue}{\sqrt{6}}\)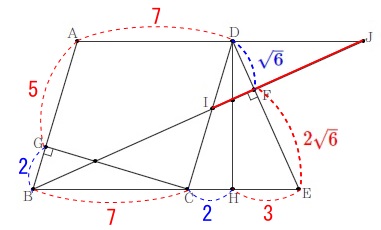なので\(\,\mathrm{△JDF}\,\)∽\(\,\mathrm{△BEF}\,\)の相似比が
\(\hspace{10pt}\mathrm{DF:EF}=\color{blue}{\sqrt{6}}:\color{red}{2\sqrt{6}}=\,\color{blue}{①}:\color{red}{②}\,\)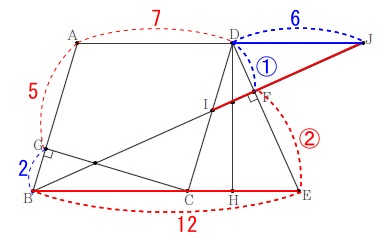これから\(\hspace{4pt}\mathrm{DJ}=\color{blue}{6}\,\)は分かります。

線分\(\,\mathrm{IJ}\,\)を含む相似は
\(\hspace{10pt}\mathrm{△JID}\,\)∽\(\,\mathrm{△BIC}\,\)
なので\(\,\mathrm{JD:BC}=\color{blue}{6}:\color{red}{7}\,\)を利用したい。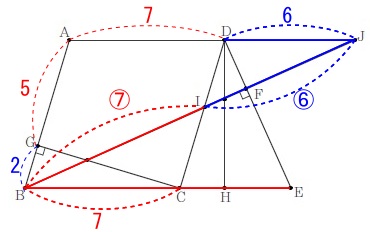線分\(\,\mathrm{BJ}\,\)が分かればいいので、直角三角形を作ります。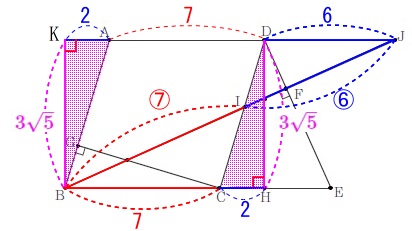直角三角形\(\,\mathrm{△DCH}\,\)と合同な三角形を加えると、
\(\,\mathrm{△BKJ}\,\)は直角三角形になるので、
（\(\,\mathrm{DH}=\color{magenta}{3\sqrt{5}}\,\)は求めてあります。）
長さなので正の平方根をとって
\(\begin{eqnarray}
\mathrm{BJ}&=&\sqrt{\mathrm{BK^2+JK^2}}\\
&=&\sqrt{(3\sqrt{5})^2+15^2}\\
&=&\sqrt{45+225}\\
&=&\sqrt{270}\\
&=&3\sqrt{30}
\end{eqnarray}\)
よって、相似比\(\,\color{blue}{6}:\color{red}{7}\,\)から
　\(\begin{eqnarray}
\mathrm{IJ}&=&\frac{\color{blue}{6}}{\color{red}{7}+\color{blue}{6}}\times \mathrm{BJ}\\
&=&\frac{6}{13}\times 3\sqrt{30}\\
&=&\underline{\underline{　\frac{18\sqrt{30}}{13}　}}\mathrm{cm}
\end{eqnarray}\)

相似比\(\,6:7\,\)から\(\,\mathrm{DC=7}\,\)を利用して\(\,\mathrm{DJ}\,\)が求まるので、
平行線を補助しても出てきそうですが、
相似の計算がかなり増えそうなのでお任せします。

第３問空間図形（立体の性質や体積など）

\(\,\large{3}\,\)
\(\,\mathrm{C}\,\)問題でも差がつきそうな立体です。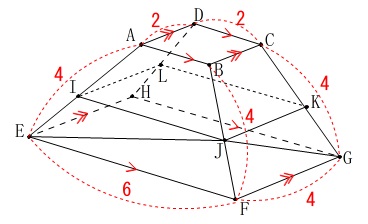条件にある合同な台形は認識しておいて下さい。

「錐台じゃない。」ということは引っかけがある？

(1)
図で与えられていますが条件が加わります。
\(\hspace{4pt}\mathrm{AI=BJ=CK=DL}\)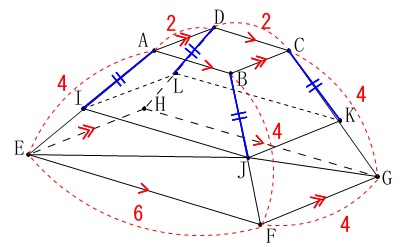①
ありました。ねじれの位置です。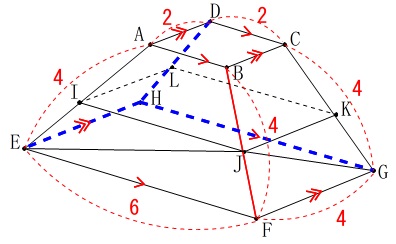辺\(\,\mathrm{\color{red}{BF}}\,\)とねじれの位置にある辺をすべて選びます。
辺\(\,\mathrm{\color{blue}{EH}\,,\,\color{blue}{GH}\,,\,\color{blue}{\underline{\,DH\,}}}\,\)がねじれの位置になります。

答え\(\hspace{4pt}\underline{　イ\,,\,エ\,,\,オ　}\)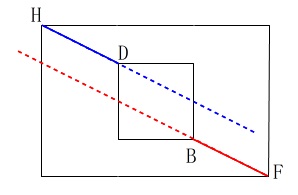真上から見るとわかりやすいですが、
錐台じゃないので直線\(\,\mathrm{DH}\,\)と直線\(\,\mathrm{BF}\,\)は交わりません。
※
錐台なら平行な面で切ったすべての断面は相似です。
（会員は錐台の体積公式が使えないので注意。）
②
三角形の面積比を求めます。
\(\,\mathrm{\color{blue}{△JFG}}\,\)の面積は\(\,\mathrm{\color{red}{△JEF}}\,\)の面積の何倍か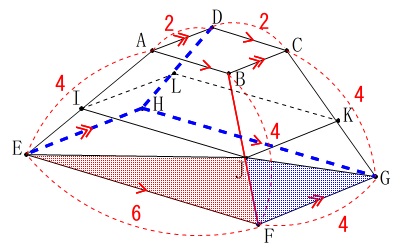？基本通り面で見ます。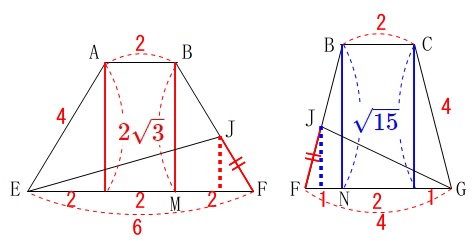それぞれの三角形の高さの比は台形の高さの比になるので、
（相似な三角形に注目して）
三平方の定理から
\(\hspace{10pt}\mathrm{\color{red}{BM}}=\sqrt{12}=\color{red}{2\sqrt{3}}\)
\(\hspace{10pt}\mathrm{\color{blue}{BN}}=\color{blue}{\sqrt{15}}\)
（ここでの\(\,\mathrm{M\,,\,N}\,\)は(2)とは違う点です。）
これから面積比は
　\(\begin{eqnarray}
\mathrm{\color{blue}{△JFG}}:\mathrm{\color{red}{△JEF}}&=&\frac{1}{2}\times 4\times \color{blue}{\sqrt{15}}:\frac{1}{2}\times 6\times \color{red}{2\sqrt{3}}\\
&=&4\sqrt{15}:6\sqrt{3}
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}
\frac{\color{blue}{\mathrm{△JFG}}}{\color{red}{\mathrm{△JEF}}}&=&\frac{4\sqrt{15}}{6\sqrt{3}}\\
&=&\underline{\underline{　\frac{\sqrt{5}}{3}　}}\,(\,倍\,)
\end{eqnarray}\)

面の傾き（倒れ方）が違うから高さが違うことに注意ですね。
③
長方形\(\,\mathrm{IJKL}\,\)の周の長さ\(\,15\,\)のとき、
辺\(\,\mathrm{JK}\,\)の長さを求めます。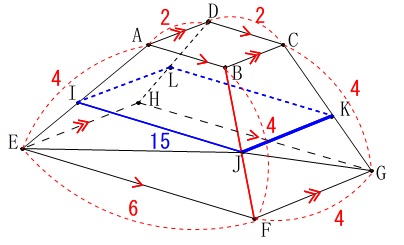申し訳ないですけど会員向け解説を先にします。
（簡単な解説で理解できるでしょう。）

２つの台形を等しい比で切り取るので、
点\(\,\mathrm{J}\,\)が辺\(\,\mathrm{BF}\,\)を\(\,a:b\,\)に内分するとします。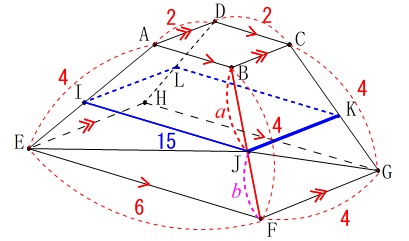このとき
\(\hspace{10pt}\displaystyle \mathrm{IJ=KL}=\frac{6a+2b}{a+b}\)
\(\hspace{10pt}\displaystyle \mathrm{JK=IL}=\frac{4a+2b}{a+b}\)
となるので
　\(\begin{eqnarray}
2\times \frac{6a+2b}{a+b}+2\times \frac{4a+2b}{a+b}&=&15\\
12a+4b+8a+4b&=&15(a+b)\\
20a+8b&=&15a+15b\\
5a&=&7b
\end{eqnarray}\)
これから
\(\hspace{10pt}a:b=7:5\)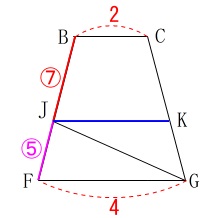つまり\(\,\mathrm{J}\,\)は辺\(\,\mathrm{BF}\,\)を\(\,7:5\,\)に内分するので
　\(\begin{eqnarray}
\mathrm{JK}&=&\frac{4\times 7+2\times 5}{7+5}\\
&=&\frac{38}{12}\\
&=&\underline{\underline{　\frac{19}{6}　}}\,\mathrm{cm}
\end{eqnarray}\)

\(\,\mathrm{C}\,\)問題を受験する会員は方針、同じじゃないですか？
公式を使わず問題の条件から部分的に長さを求めに行きましょう。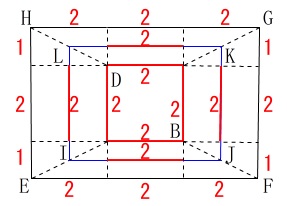立体を上から見た場合を利用しますが、
対称性から１つの隅の長さだけ見た方がすっきりします。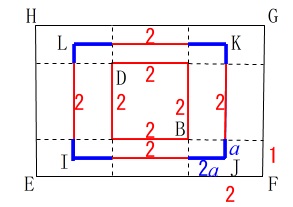青線の長さは\(\,\mathrm{EF}\,\)側と\(\,\mathrm{FG}\,\)側では\(\,2:1\,\)になります
短い方を\(\,\color{blue}{a}\,\)とすると長い方が\(\,\color{blue}{2a}\,\)で四隅にあるから、
正方形の４辺が間に入ることを考えると周の長さの関係から
　\(\begin{eqnarray}
\color{red}{2}\times 4+(\color{blue}{2a}+\color{blue}{a})\times 4&=&15\\
8+12\,\color{blue}{a}&=&15\\
12\,\color{blue}{a}&=&7\\
\color{blue}{a}&=&\color{blue}{\frac{7}{12}}
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}
\mathrm{JK}&=&\color{red}{2}+2\times \color{blue}{a}\\
&=&2+2\times \color{blue}{\frac{7}{12}}\\
&=&2+\frac{7}{6}\\
&=&\underline{\underline{　\frac{19}{6}　}}\,\mathrm{cm}
\end{eqnarray}\)

後に続く問題から考えればこっちの方が良いかな、
と思えますがどちらでも良いです。
(2)
垂線の長さ\(\,\mathrm{BM}\,\)は立体の高さとなります。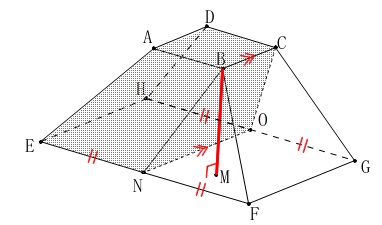①
線分\(\,\mathrm{BM}\,\)を求めます。

高さを求める事になるので直角三角形を見つけることになりますが、
どれと決まっているわけではありませんので適当なものがあればそれでいいです。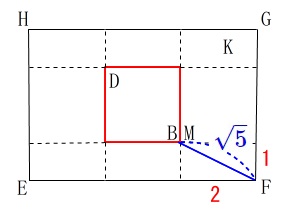真上からみた図から、
線分\(\,\mathrm{MF}\,\)が\(\,\color{blue}{\sqrt{5}}\,\)というのはすぐに分かるので、
\(\,\mathrm{△BMF}\,\)が早いですね。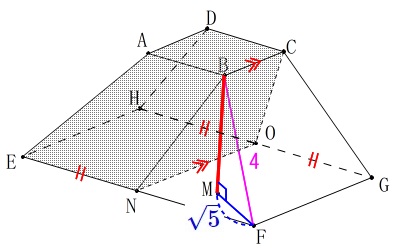三平方の定理から
　\(\begin{eqnarray}
\mathrm{BM}&=&\sqrt{\mathrm{BF^2-MF^2}}\\
&=&\sqrt{\color{magenta}{4}^2-(\,\color{blue}{\sqrt{5}}\,)^2}\\
&=&\underline{　\sqrt{11}　}\mathrm{cm}
\end{eqnarray}\)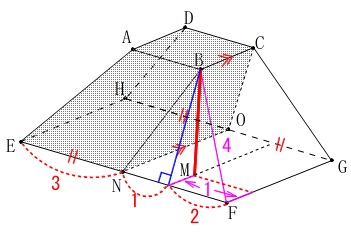台形\(\,\mathrm{AEFB}\,\)で\(\,\mathrm{B}\,\)から\(\,\mathrm{EF}\,\)に垂線引いても出てくるので、
やってみて下さい。上から見た対称性は確認しておきましょう。
②
体積ですが錐台ではないので公式は使えません。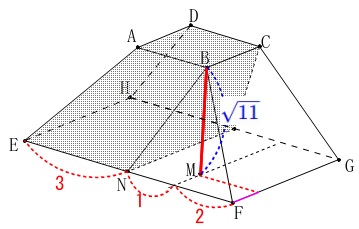立体の高さは\(\,\color{blue}{\sqrt{11}}\,\)で固定で考えられますね。

公式が使えないのでいつも通りの方針ですが、
求めたい方をブツブツ切るのもメンドウなので、
全体から部分を引くことにします。
（個人的には\(\,\mathrm{△BCM}\,\)を含む面で切りたいです。）

先ずは全体となる立体\(\,\mathrm{ABCD-EFGH}\,\)の体積を求めましょう。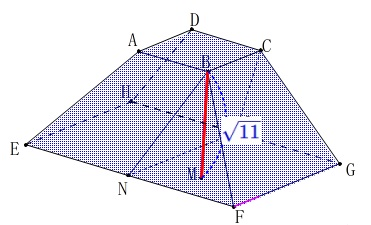これもパッと出てくれば良いのですがそういうわけにもいきません。

部分ごとの体積を求めて足します。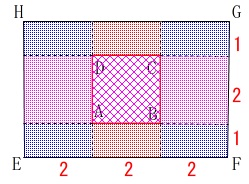色分けした同じ色の部分は対称性から同じ体積です。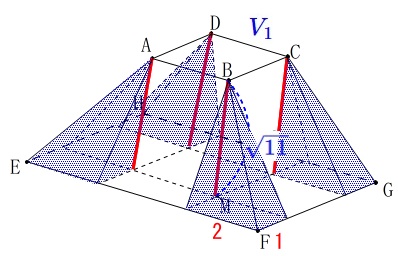四隅の４つの四角錐の体積の和\(\,\color{blue}{V_1}\,\)は、
　\(\begin{eqnarray}
\color{blue}{V_1}&=&\frac{1}{3}\times 2\times 1\times \sqrt{11}\times 4\\
&=&\color{blue}{\frac{8\sqrt{11}}{3}}
\end{eqnarray}\)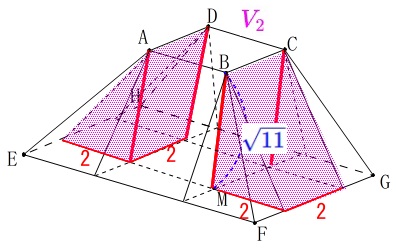線分\(\,\mathrm{AD}\,\)と線分\(\,\mathrm{BC}\,\)を高さとする三角柱２つの体積の和\(\,\color{magenta}{V_2}\,\)は
　\(\begin{eqnarray}
\color{magenta}{V_2}&=&\frac{1}{2}\times 2\times \sqrt{11}\times 2\times 2\\
&=&\color{magenta}{4\sqrt{11}}
\end{eqnarray}\)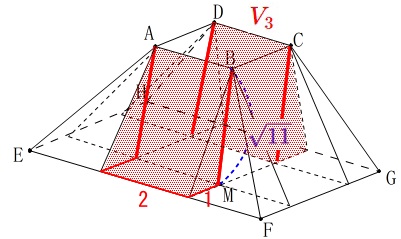線分\(\,\mathrm{AB}\,\)と線分\(\,\mathrm{DC}\,\)を高さとする三角柱２つの体積の和\(\,\color{red}{V_3}\,\)は
　\(\begin{eqnarray}
\color{red}{V_3}&=&\frac{1}{2}\,1\times \sqrt{11}\times 2\times 2\\
&=&\color{red}{2\sqrt{11}}
\end{eqnarray}\)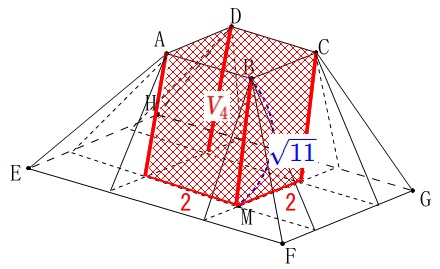正方形\(\,\mathrm{ABCD}\,\)を底面とする四角柱の体積\(\,\color{red}{V_4}\,\)は
　\(\begin{eqnarray}
\color{red}{V_4}&=&2\times 2\times \sqrt{11}\\
&=&\color{red}{4\sqrt{11}}
\end{eqnarray}\)
よって立体\(\,\mathrm{ABCD-EFGH}\,\)の体積\(\,V_5\,\)は
　\(\begin{eqnarray}
V_5&=&\color{blue}{V_1}+\color{magenta}{V_2}+\color{red}{V_3}+\color{red}{V_4}\\
&=&\color{blue}{\frac{8\sqrt{11}}{3}}+\color{magenta}{4\sqrt{11}}+\color{red}{2\sqrt{11}}+\color{red}{4\sqrt{11}}\\
&=&\frac{8\sqrt{11}}{3}+10\sqrt{11}\\
&=&\frac{38\sqrt{11}}{3}
\end{eqnarray}\)
※
色分け失敗したなあ、と思うけどこれ以上時間を割くような部分じゃないのでこのまま。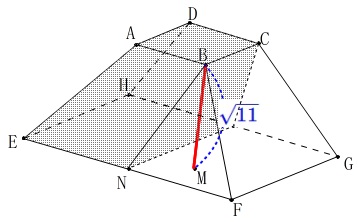今度は白い部分の体積を求めて引きます。
台形\(\,\mathrm{BNOC}\,\)を含む平面で切ったときの\(\,\mathrm{FG}\,\)側の立体です。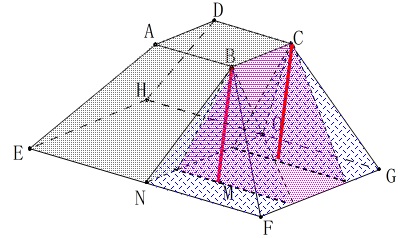四角錐２つと三角柱が１つあります。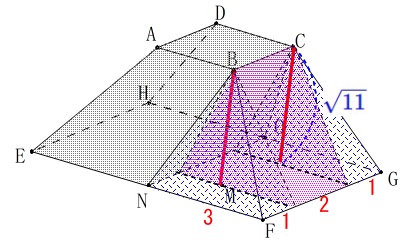この部分の体積を\(\,V_6\,\)とすると
　\(\begin{eqnarray}
V_6&=&\color{blue}{\frac{1}{3}\times 3\times 1\times \sqrt{11}}\times 2+\color{magenta}{\frac{1}{2}\times 3\times \sqrt{11}\times 2}\\
&=&2\sqrt{11}+3\sqrt{11}\\
&=&5\sqrt{11}
\end{eqnarray}\)
よって求める体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&V_5-V_6\\
&=&\frac{38\sqrt{11}}{3}-5\sqrt{11}\\
&=&\underline{\underline{　\frac{23\sqrt{11}}{3}　}}\mathrm{cm^3}
\end{eqnarray}\)