三重県公立高校入試2018年度後期試験数学の問題と解説(後半)

2018年(平成30年)度に三重県で行われた公立高校入試後期試験の数学の問題と解説(後半)です。
後半は図形総合問題となるのは前期選抜試験と同じです。
作図から合同、相似な図形から長さや面積の比、立体の体積利用まで幅広く問われています。

問題は三重県で公開してくれています。

⇒　2018年三重県公立高校入試後期選抜試験の数学問題

作図と立体の辺の長さと体積の利用

　\(\color{blue}{\fbox{　4　}}\)

(1)
\(\,60°\,\)の作図です。

作図で利用する方法は限られています。

角の二等分線や垂線の引き方は覚えているでしょう。
あと、円や三角定規も作図できるのでどれかを利用すると考えて取り組むとなんとかなります。笑

直線のなす角が\(\,180°\,\)なので\(\,90°\,\)や\(\,45°\,\)の作図は角の二等分線の作図を繰り返せば良いのですが、
\(\,60°\,\)という角は角の二等分線だけではなかなか出てきません。

\(\,60°\,\)といえば正三角形です。
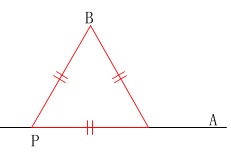図のように正三角形が作図できれば良いのですが、うまくいきません。

そこで、
\(\,\mathrm{B}\,\)から\(\,\ell\,\)に垂線を引いて、
\(\,\ell\,\)との交点を\(\,\mathrm{H}\,\)とすると\(\,\mathrm{∠PBH=30^{\circ}}\,\)となれば、
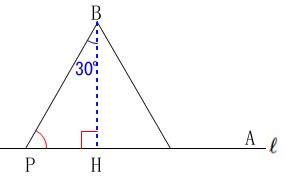\(\,\mathrm{∠APB=60^{\circ}}\,\)となることを利用します。

①\(\,\mathrm{B}\,\)から\(\,\ell\,\)に垂線を引き、

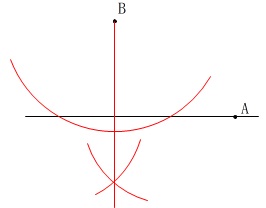
②その垂線の一部を\(\,1\,\)辺とする正三角形を作り、

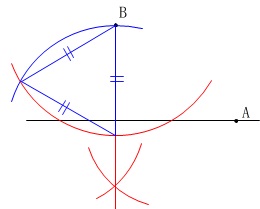
③\(\,\color{magenta}{角の二等分線を引いて}\,\)\(\,\mathrm{P}\,\)を決定します。
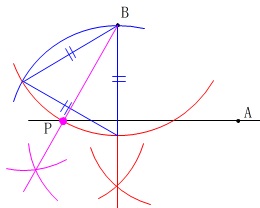作図に\(\,\mathrm{A}\,\)の位置は関係ありません。

(2)
立方体の中にある三角錐の問題です。
ここまでは普通の問題なので確実に得点して最後の\(\color{black}{\fbox{　5　}}\)に時間を余らせておきましょう。

簡単ので解説も簡単に済ませます。

立体の中にある点の条件は、

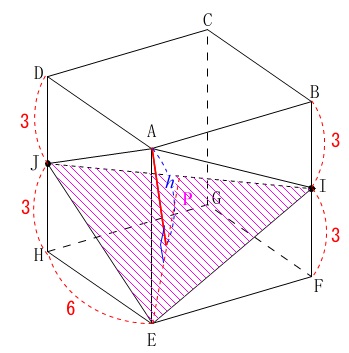
　\(\,\mathrm{ABCD-EFGH}\,\)は\(\,1\,\)辺\(\,6\,\)の立方体
　\(\,\mathrm{I}\,\)は\(\,\mathrm{BF}\,\)の中点
　\(\,\mathrm{J}\,\)は\(\,\mathrm{DH}\,\)の中点
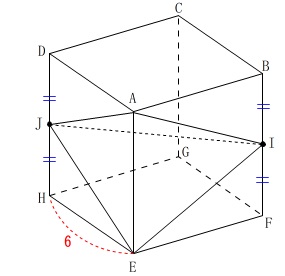分かる長さは書き込んでおくと問題に取り組みやすくなりますよ。
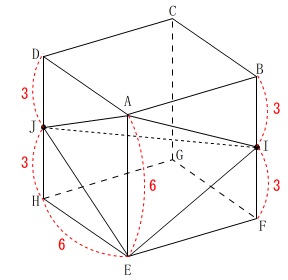これからほとんどの長さと面積と体積は出せますが、
時間のムダになるので問題に合わせて求めていくことにします。

①
辺\(\,\mathrm{EJ}\,\)は直角三角形\(\,\mathrm{JHE}\,\)の斜辺です。
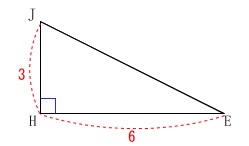三平方の定理を用いて、

　\(\begin{eqnarray}
\mathrm{EJ}^2&=&\mathrm{JH^2+EH^2}\\
&=&3^2+6^2\\
&=&9+36\\
&=&45\\
\mathrm{EJ}&=&\pm 3\sqrt{5}
\end{eqnarray}\)

\(\,\mathrm{EJ}\,\)は長さなので\(\,\mathrm{EJ\,＞\,0}\,\)だから、

　\(\,\mathrm{EJ}=\underline{　3\sqrt{5}　}\,\)

②
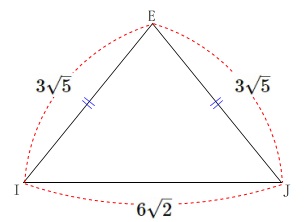
\(\,\mathrm{△EIJ}\,\)は\(\,\mathrm{EJ=EI}\,\)の二等辺三角形です。

①から
　\(\,\mathrm{EJ=EI=3\sqrt{5}}\,\)
は分かっています。

辺\(\,\mathrm{IJ}\,\)は中点どうしを結んでいるので\(\,1\,\)辺\(\,6\,\)の正方形の対角線になるから、
　\(\mathrm{IJ}=6\sqrt{2}\)
は計算しなくても分かるとは思いますが、三平方の定理で丁寧に求めておくと、
　\(\begin{eqnarray}
\mathrm{IJ^2}&=&\mathrm{AB^2+AD^2}\\
&=&6^2+6^2\\
&=&72\\
&=&6\sqrt{2}　(\,\mathrm{IJ}\,＞\,0\,)
\end{eqnarray}\)
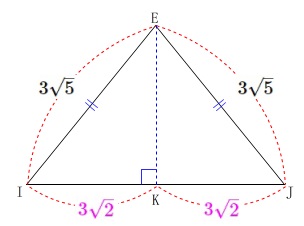
このとき頂点\(\,\mathrm{E}\,\)の角の二等分線は底辺\(\,\mathrm{IJ}\,\)と垂直に交わり、
底辺\(\,\mathrm{IJ}\,\)を\(\,2\,\)等分します。

このとき、底辺との交点を\(\,\mathrm{K}\,\)とすると
　\(\begin{eqnarray}\displaystyle
\mathrm{JK}&=&\frac{1}{2}\times \mathrm{IJ}\\
&=&\frac{1}{2}\times 6\sqrt{2}
&=&\color{magenta}{3\sqrt{2}}\,
\end{eqnarray}\)
\(\,\mathrm{△EIK}\,\)に三平方の定理を用いて、

　\(\begin{eqnarray}
\mathrm{IK^2+EK^2}&=&\mathrm{EI^2}\\
(\color{magenta}{3\sqrt{2}})^2+\mathrm{EK}^2&=&(3\sqrt{5})^2\\
18+\mathrm{EK}^2&=&45\\
\mathrm{EK}^2&=&45-18\\
&=&27\\
\mathrm{EK}=\pm \,3\sqrt{3}
\end{eqnarray}\)

\(\,\mathrm{EK\,＞\,0}\,\)なので、\(\,\mathrm{EK=\color{blue}{3\sqrt{3}}}\,\)
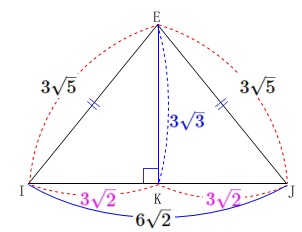このことから\(\,\mathrm{△EIJ}\,\)は、
　底辺を\(\,\mathrm{IJ}\,\)、高さを\(\,\mathrm{EK}\,\)
とする三角形なので面積は、

　\(\begin{eqnarray}\displaystyle
\mathrm{△EIJ}&=&\frac{1}{2}\times \mathrm{IJ}\times \mathrm{EK}\\
&=&\frac{1}{2}\times 6\sqrt{2}\times \color{blue}{3\sqrt{3}}\\
&=&\underline{　9\sqrt{6}　}　(\mathrm{cm^2})
\end{eqnarray}\)

面積や体積は底辺や底面の見方を変えても変わらない

③
三角すいの体積は転がしても変わらない、という性質を利用します。

⇒　円錐(すい)の表面積や四角錐,五角錐の体積の求め方

錐体の体積の求め方は復習しておきましょう。

三角すい\(\,\mathrm{P}\,\)は\(\,\mathrm{△AEI}\,\)または\(\,\mathrm{△AEJ}\,\)を底面とし、
高さを立方体の\(\,1\,\)辺\(\,6\,\)とする立体です。
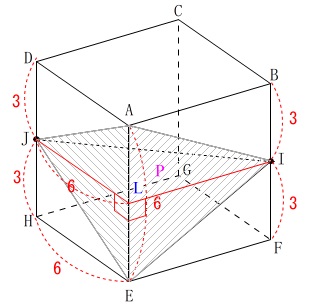三角すい\(\,\mathrm{P}\,\)の体積\(\,\mathrm{V}\,\)は、

　\(\begin{eqnarray}
\mathrm{V}&=&\frac{1}{3}\times \mathrm{△AEJ}\times \mathrm{IL}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 6\times 6\\
&=&\color{red}{36}
\end{eqnarray}\)

この計算は結果までしなくても良いのですが、置きかえやすく済ませておきました。

次に、\(\,\mathrm{△EIJ}\,\)を底面としたときの三角すい\(\,\mathrm{P}\,\)の高さを求めますが、
三角すい\(\,\mathrm{P}\,\)の体積は変わらないので\(\,\color{red}{36}\,\)です。

底面を\(\,\mathrm{△EIJ}\,\)としたときの三角すい\(\,\mathrm{P}\,\)の高さを\(\,\color{blue}{h}\,\)とすると、
②から\(\,\mathrm{△EIJ=\color{magenta}{9\sqrt{6}}}\,\)と分かっているので、

　\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{1}{3}\times \mathrm{△EIJ}\times \color{blue}{h}\\
\color{red}{36}&=&\frac{1}{3}\times \color{magenta}{9\sqrt{6}}\times \color{blue}{h}\\
\color{red}{36}\times 3&=&\color{magenta}{9\sqrt{6}}\times \color{blue}{h}\\
\color{magenta}{9\sqrt{6}}\times \color{blue}{h}&=&\color{red}{36}\times 3\\
\color{blue}{h}&=&\frac{\color{red}{36}\times 3}{\color{magenta}{9\sqrt{6}}}\\
&=&\frac{12}{\sqrt{6}}\\
&=&\underline{　2\sqrt{6}　}　(\mathrm{cm})
\end{eqnarray}\)

\(\color{black}{\fbox{　4　}}\)はここまでですが良くある問題なのでそれほど時間はかからないでしょう。

差が出るのは次の\(\color{black}{\fbox{　5　}}\)ですね。
しっかり手を動かして下さい。

合同と相似の証明と線分比と面積比

　\(\color{blue}{\fbox{　5　}}\)

問題にある図形の条件は前期と同様にシンプルですが、
一般入試としては差が出る問題です。

図形の条件を書き出しておきます。

条件

　円\(\,\mathrm{O}\,\)は直径が\(\,\mathrm{AB}\,\)
　\(\,\mathrm{DC}\,\)も中心を通るので円\(\,\mathrm{O}\,\)の直径
　\(\,\mathrm{AG}\,\)は\(\,\mathrm{∠CAB}\,\)の二等分線
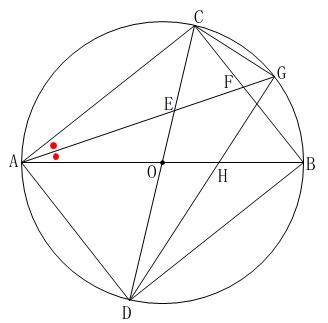言えることが多すぎて迷うのは前期試験と同じです。笑

こういう条件が多いときは何を使えば効果的かは分かりませんので、
やみくもに解いても時間がかかりすぎますので、
問題の聞いてくる順番通りに見ていきましょう。

(1)
\(\,\mathrm{△AOE}\,\)と\(\,\mathrm{△DOH}\,\)が合同がであることを証明しますが、
\(\,\color{black}{\fbox{(ア)}}\,\)から\(\,\color{black}{\fbox{(ウ)}}\,\)をうめれば良いので考えることはほとんどありません。

合同の証明や相似の証明は図の中で完成させておきましょう。
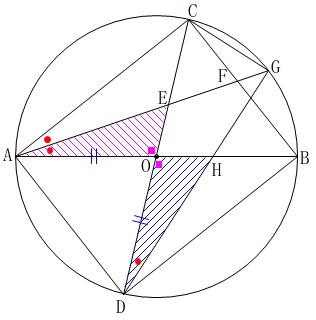角の二等分線による等しい角と円周角が等しいことをつなげれば終わりです。

証明は自分の言葉でつなげていけば良いですが、この問題は穴埋めなので問題文通りにうめていきます。

〈証明〉\(\,\mathrm{△AOE}\,\)と\(\,\mathrm{△DOH}\,\)において
円\(\,\mathrm{O}\,\)の半径だから、　\(\,\mathrm{\color{blue}{OA}=\color{blue}{OD}　･･･①}\,\)
対頂角は等しいから、　\(\,\mathrm{∠AOE=\color{magenta}{∠DOH}　･･･②}\,\)
線分AGは∠CABの二等分線だから、　\(\,\mathrm{∠EAO}=\mathrm{\color{red}{∠CAG}}　･･･③\,\)
弧CGに対する円周角は等しいから、　\(\,\mathrm{\color{red}{∠CAG}=∠HDO　･･･④}\,\)
③,④より、　\(\,\mathrm{∠EAO=∠HDO　･･･⑤}\,\)
①,②,⑤より、\(\,1\,\)組の辺とその両端の角がそれぞれ等しいので、
　\(\,\mathrm{△AOE}\,\)　≡　\(\,\mathrm{△DOH}\,\)

\(\color{black}{\fbox{(ア)}}\)　\(\,\mathrm{\underline{　∠DOH　}}\,\)
\(\color{black}{\fbox{(イ)}}\)　\(\,\mathrm{\underline{　∠CAG　}}\,\)
\(\color{black}{\fbox{(ウ)}}\)　\(\,\underline{　1\,組の対辺とその両端の角　}\,\)

図の中で、
　\(\,1\,\)組の辺とその両端角がそれぞれ等しくなっている
ことに気がついたら、合同の対応する記号順にうめていけば考えることはありません。

(2)
今度は\(\,\mathrm{△ADH}\,\)と\(\,\mathrm{△GCE}\,\)が相似であることの証明です。
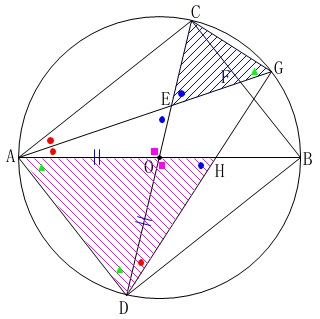(1)で示した合同な三角形を二等辺三角形\(\,\mathrm{OAD}\,\)にひっつけたことを利用すれば条件を並べることもなく相似だと分かりますが、
相似の証明では相似条件をそろえていきましょう。

（証明）
　\(\,\mathrm{△ADH}\,\)　と　\(\,\mathrm{△GCE}\,\)　において、
半径は等しいので\(\,\mathrm{OA=OD}\,\)で、
\(\,\mathrm{△OAD}\,\)が二等辺三角形であることから、
　\(\mathrm{∠OAD=∠ODA}　･･･①\)
弧\(\,\mathrm{AC}\,\)の円周角から
　\(\,\mathrm{∠ADC=∠CGE}　･･･②\,\)
①②から\(\,\mathrm{∠DAH}\,\)と\(\,\mathrm{∠CGE}\,\)が等しいことが言える。
　\(\mathrm{\color{green}{∠DAH}=\color{green}{∠CGE}}　･･･③\)
また、\(\,\mathrm{△AOE}\,\)　≡　\(\,\mathrm{△DOH}\,\)であることから
　\(\,\mathrm{∠AEO=∠DHO　･･･④}\,\)
対頂角は等しいので、
　\(\,\mathrm{∠AEO=∠CEG　･･･⑤}\,\)
④⑤は\(\,\mathrm{∠DHA}\,\)と\(\,\mathrm{∠CEG}\,\)が等しいことを示しているので、
　\(\,\mathrm{\color{blue}{∠DHA}=\color{blue}{∠CEG}　･･･⑥}\,\)
③⑥より、
　\(\,2\,\)組の角がそれぞれ等しい
ので、
　\(\,\mathrm{△ADH}\,\)　∽　\(\,\mathrm{△GCE}\,\)
（証明終わり）

他にも四角形\(\,\mathrm{ADBC}\,\)が長方形であることや、
直線\(\,\mathrm{OG}\,\)が対称の軸になっていることなど、
いろいろなことが言えるのですが省略します。

問題が必要なことを順番に導いてくれるので、最低限の補助線で終わります。

補助線の引き方取り方

(3)
ここで初めて長さが与えられます。

　\(\,\mathrm{AB=10}\,\)
　\(\,\mathrm{BC=6}\,\)
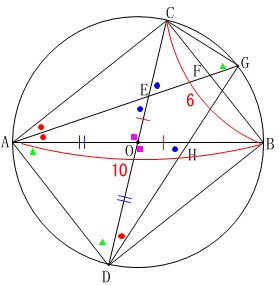ちょっと応用が入りますので、簡単に求まる長さは出しておきます。

直径に対する円周角は\(\,90°\,\)で\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ADC}\,\)は直角三角形で、
三平方の定理から、
　\(\,\mathrm{AC=8}\,\)
　\(\,\mathrm{AD=6}\,\)
半径は常に等しく、
　\(\,\mathrm{OA=OC=OD=5}\,\)
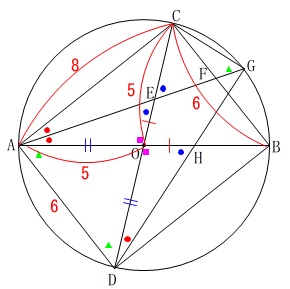相似や合同な図形がいくつかあり、
何を求めるかで違ってくるので問題に入ります。

①
線分\(\,\mathrm{OE}\,\)の長さです。

『覚え太郎』会員は角の二等分線定理を知っているので、

　\(\begin{eqnarray}\displaystyle
\mathrm{AO:AC}&=&\mathrm{OE:EC}\\
5:8&=&\mathrm{OE:EC}
\end{eqnarray}\)
から
　\(\begin{eqnarray}
\mathrm{OE}&=&\frac{5}{8+5}\times \mathrm{OC}\\
&=&\frac{5}{13}\times 5\\
&=&\underline{　\frac{25}{13}　}　(\mathrm{cm})
\end{eqnarray}\)

で良いです。

知らない人は、
　長さを求めるときの補助線は平行線か垂線
と考えておくと良いですよ。

\(\,\mathrm{E}\,\)を通り\(\,\mathrm{AO}\,\)に平行になるように補助線を引いて、
\(\,\mathrm{AC}\,\)との交点を\(\,\mathrm{I}\,\)とします。
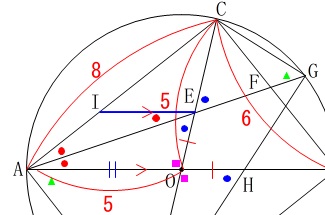\(\,\mathrm{AE}\,\)は\(\,\mathrm{∠CAO}\,\)の二等分線なので、錯角が等しいことから、
\(\,\mathrm{△AIE}\,\)は二等辺三角形になります。

ここで、\(\,\mathrm{AI}=x\,\)とすると
　\(\,\mathrm{IE}=x\,\)
　\(\,\mathrm{CI=}8-x\,\)
となります。

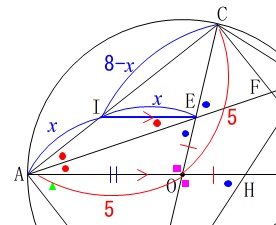\(\,\mathrm{△CIE}\,\)　∽　\(\,\mathrm{△CAO}\,\)　なので、

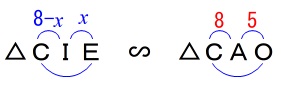
　\(\begin{eqnarray}\displaystyle
\mathrm{CI:CA}&=&\mathrm{IE:AO}\\
(8-x):8&=&x:5\\
8x&=&5(8-x)\\
&=&40-5x\\
13x&=&40\\
x&=&\frac{40}{13}
\end{eqnarray}\)

このとき
　\(\begin{eqnarray}
\mathrm{IC}&=&8-x\\
&=&8-\frac{40}{13}\\
&=&\frac{104-40}{13}\\
&=&\frac{64}{13}
\end{eqnarray}\)

よって、\(\,\mathrm{IE}\, /\!/ \,\mathrm{AO}\,\)から

　\(\begin{eqnarray}\displaystyle
\mathrm{CE:OE}&=&\mathrm{CI:AI}\\
&=&\frac{64}{13}:\frac{40}{13}\\
&=&8:5
\end{eqnarray}\)

となるので、

　\(\begin{eqnarray}
\mathrm{OE}&=&\frac{5}{8+5}\times \mathrm{OC}\\
&=&\frac{5}{13}\times 5\\
&=&\underline{　\frac{25}{13}　}
\end{eqnarray}\)

角の二等分線定理は知らなくても求まりますが、
定理を使えばだんぜん早いです。

②
線分\(\,\mathrm{AE}\,\)と\(\,\mathrm{EG}\,\)の線分比ですがうまく使える相似が見抜きにくいです。
しかし補助線の入れ方で簡単に答えが出ます。

①から線分\(\displaystyle \,\mathrm{OE}=\color{red}{\frac{25}{13}}\,\)で、
(1)の合同から\(\,\mathrm{△OEM}\,\)が二等辺三角形なので、
二等辺三角形\(\,\mathrm{OAD}\,\)と相似だから錯角が等しく、
線分\(\,\mathrm{EM}\,\)は\(\,\mathrm{AD}\,\)と平行になります。
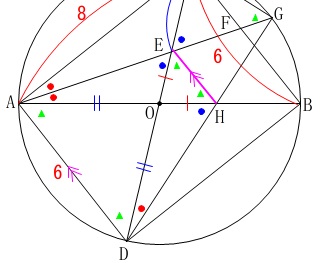このとき\(\,\mathrm{△GEH}\,\)　∽　\(\,\mathrm{△GAD}\,\)なので、
　\(\,\mathrm{GE:GA=EH:AD}\,\)
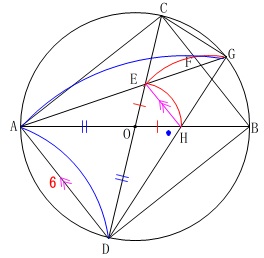線分\(\,\mathrm{EH}\,\)の長さは分からないので、（求めていないだけです。笑）
　\(\,\mathrm{△OEH}\,\)　∽　\(\,\mathrm{△ODA}\,\)
だから
　\(\,\mathrm{EH:DA=OE:OD}\,\)
に切り換えます。

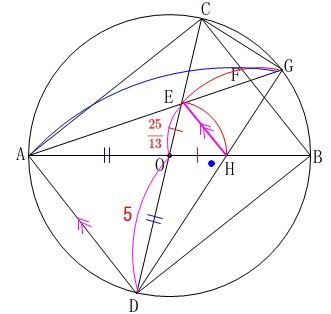
　\(\begin{eqnarray}
\mathrm{EH:DA}&=&\mathrm{OE:OD}\\
&=&\frac{25}{13}:5\\
&=&25:5\times 13\\
&=&\color{blue}{5}:\color{blue}{13}
\end{eqnarray}\)
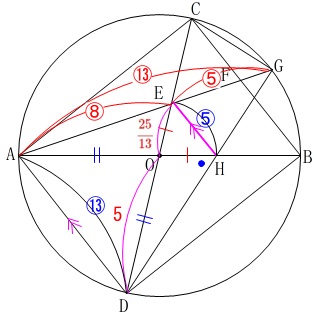　\(\,\mathrm{GE:GA=\color{red}{5}:\color{red}{13}}\,\)
よって、
　\(\mathrm{AE:EG}=\underline{　8:5　}\)

③
相似な図形の面積比ですがこれも相似比が分かっていません。

\(\,\mathrm{△ADH}\,\)と\(\,\mathrm{△DAE}\,\)は同じ面積なので、
\(\,\mathrm{△DAE}\,\)と\(\,\mathrm{△GCE}\,\)の面積を比べます。

②から\(\,\mathrm{AE:EG=\color{red}{⑧}:\color{red}{⑤}}\,\)であることと、

　\(\begin{eqnarray}
\mathrm{DE:EC}&=&5+\frac{25}{13}:5-\frac{25}{13}\\
&=&\frac{65+25}{13}:\frac{65-25}{13}\\
&=&90:40\\
&=&\color{blue}{⑨}:\color{blue}{④}
\end{eqnarray}\)
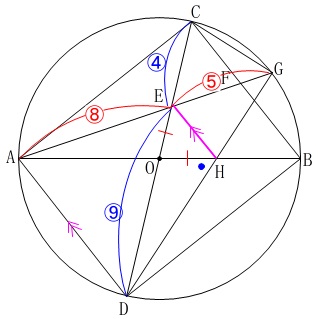なので、
　\(\begin{eqnarray}
\mathrm{△ADH:△GCE}&=&\mathrm{△ADE:△GCE}\\
&=&\color{red}{⑧}\times \color{blue}{⑨}:\color{red}{⑤}\times \color{blue}{④}\\
&=&\underline{　18:5　}
\end{eqnarray}\)

『覚え太郎』会員はこれでいいです。

別の方法として、
三角形を基準にして面積比を出す方法をお伝えしておきます。

基準にする三角形はいくつか考えられますが、底辺が同じ\(\,\mathrm{AG}\,\)で進めてみます。

先ずは\(\,\mathrm{△ADG}\,\)を基準にします。

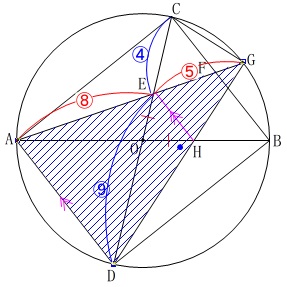
　\(\begin{eqnarray}
\mathrm{△ADH}&=&\mathrm{△AED}\\
&=&\frac{8}{8+5}\times \mathrm{△ADG}\\
&=&\color{red}{\frac{8}{13}}\times \mathrm{△ADG}
\end{eqnarray}\)

今度は\(\,\mathrm{△GCE}\,\)を含む\(\,\mathrm{△ACG}\,\)から見ます。
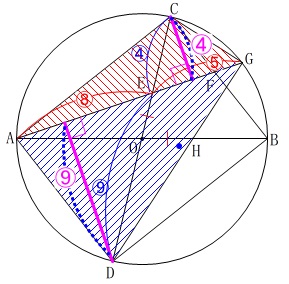線分比\(\,\mathrm{DE:CE=\color{blue}{9}:\color{blue}{4}}\,\)だから、
\(\,\mathrm{△ADG}\,\)と\(\,\mathrm{ACG}\,\)の底辺を\(\,\mathrm{AG}\,\)と見ると、
高さの比も\(\,\color{magenta}{9}:\color{magenta}{4}\,\)なので

　\(\displaystyle \mathrm{△ACG}=\color{magenta}{\frac{4}{9}}\times \mathrm{△ADG}\)

また、\(\,\mathrm{AE:EG=8:5}\,\)なので、
　\(\displaystyle \mathrm{△GCE}=\color{blue}{\frac{5}{13}}\times \mathrm{△ACG}\)
だから、
　\(\begin{eqnarray}\displaystyle
\mathrm{△GCE}&=&\color{blue}{\frac{5}{13}}\times \mathrm{△ACG}\\
&=&\color{blue}{\frac{5}{13}}\times\color{magenta}{\frac{4}{9}}\times \mathrm{△ADG}\\
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}
\mathrm{△ADH}:\mathrm{△GCE}&=&\color{red}{\frac{8}{13}}:\color{blue}{\frac{5}{13}}\times\color{magenta}{\frac{4}{9}}\\
&=&72:20\\
&=&\underline{　18:5　}
\end{eqnarray}\)

もう少し図を入れて詳しくした方が分かり易いでしょうけど、
自分で図を書いて確認して下さい。

これは1つの方法でしかありません。
数学の解法は1つではありませんので、自分でやってみた方法が合っているかどうかは学校の先生にでも聞いて下さい。
会員の方は私に聞いて下さい。

\(\,2018\,\)年三重県後期選抜試験の数学問題は以上です。

⇒　三重県公立高校入試2018年度後期試験数学の問題と解説（前半）

前半から見直して、時間配分を考えて目標点数をとって下さいね。
満点狙うなら、\(\color{black}{\fbox{　5　}}\,\)には少し時間をかけられるように、
前半の基本問題を素早く確実に解いておくことです。

⇒　三重県公立高校入試(2018年)前期選抜試験数学の問題と解説

\(\,2018\,\)年前期選抜試験はほとんど同じ問題構成です。
計算の量は前期の方が若干多い、と思える程度ですが過去問を解いて傾向を知るのなら前期後期両方見ておいた方が良いですよ。

⇒　三重県公立高校入試の数学の問題と解説

\(\,2019\,\)年度の問題も（いつか？笑）解説しますので、見ておくと良いです。
（遅くなりましたが解説しました。）