和歌山県公立高校入試2018年数学の過去問題と解説

2018年（平成30年）度に和歌山県で行われた公立高校入試数学の過去問題と解説です。
問題は全部で大問5題ですが、答えはきれいな数字ばかりですので方針を立てられれば満点は十分に狙えます。
満点を狙わない人は配点に注意して目標点数をどうやってとるかを計画しておくと良いです。

問題は和歌山県で公開してくれています。

⇒　2018年和歌山県公立高校入試数学の問題

計算の小問集合

　\(\color{blue}{\fbox{　1　}}\)

〔問\(\,1\,\)〕
「計算しなさい。」です。
規則通りに計算すればすぐに終わります。

(1)
正の数負の数の加減です。

　\(\hspace{10pt}-9+3\\
=\underline{　-6　}\)

正の数負の数の加減は数直線で見れば確実ですね。

⇒　正の数負の数の加法と減法と分数の計算問題のポイント

(2)
分数の足し算と割り算です。

　\(\hspace{10pt}\displaystyle \frac{1}{2}+2\div \left(-\frac{4}{5}\right)\\
\displaystyle =\frac{1}{2}\color{red}{-}2\color{red}{\times \frac{5}{4}}\\
\displaystyle =\frac{1}{2}-\frac{5}{2}\\
\displaystyle =\frac{-4}{2}\\
=\underline{　-2　}\)

割り算は逆数のかけ算です。
符号には注意しておきましょう。

⇒　分数の文字式計算問題をはやく処理するコツとポイント(中学1年)

文字式でも処理方法は同じです。

(3)
展開して同類項をまとめるだけです。

　\(\hspace{10pt} -2(a-4)+5(a-3)\\
=-2a+8+5a-15\\
=\underline{　3a-7　}\)

(4)
無理数の有理化と引き算です。

　\(\hspace{10pt}\displaystyle \frac{30}{\sqrt{6}}-\sqrt{24}\\
\displaystyle =\frac{30\times\color{red}{\sqrt{6}}}{\sqrt{6}\times \color{red}{\sqrt{6}}}-\color{blue}{2\sqrt{6}}\\
\displaystyle =\frac{30\sqrt{6}}{6}-2\sqrt{6}\\
=5\sqrt{6}-2\sqrt{6}\\
=\underline{　3\sqrt{6}　}\)

⇒　近似値とは？ルートのついた無理数の分母の有理化と近似値の使い方

無理数の有理化と同時に、近似値までの利用を復習しておくと良いです。

\(\sqrt{24}=\color{blue}{2\sqrt{6}}\)
としている部分の素因数分解はミスを減らすためにも確実にやっておいた方が良いですよ。

(5)
文字式の展開ですが、公式を利用すると早いというだけで、ひとつひとつ展開しても大して変わりません。
確実に展開しましょう。

　\(\hspace{10pt}x(x+2y)-\color{red}{(x+3y)(x-3y)}\\
=x^2+2xy-\color{red}{(x^2-9y^2)}\\
=x^2+2xy-x^2+9y^2\\
=\underline{　2xy+9y^2　}\)

公式を使わない場合でも同じです。

　\(\hspace{10pt}x(x+2y)-\color{red}{(x+3y)(x-3y)}\\
=x^2+2xy-\color{red}{(x^2-3xy+3xy+9y^2)}\\
=x^2+2xy-\color{red}{(x^2-9y^2)}\\
=x^2+2xy-x^2+9y^2\\
=\underline{　2xy+9y^2　}\)

\(\,1\,\)行増えるだけでかかる時間はたいして変わりません。
ただし、因数分解もできないと厳しい公式ですので利用できるようになっておいた方が良いです。

それと、（かっこ）を外すときの符号の変化には気をつけましょう。

〔問\(\,2\,\)〕
\(\,2\,\)次方程式の解を求めます。

　\(\begin{eqnarray}
(x+3)^2&=&2\\
x+3&=&\pm \sqrt{2}\\
x&=&\underline{　-3\pm \sqrt{2}　}
\end{eqnarray}\)

展開して解の公式でも良いですけど、平方完成型なのでそのまま利用した方がはやいです。

⇒　２次方程式を平方根と文字の置きかえを利用して解く方法(中３)

方程式を解くことと、方程式の解を求めることは同じことですよ。

⇒　方程式の解とは？2次方程式の係数と他の解を求める代入問題の解き方

\(\,2\,\)次方程式の解は2つあるので気をつけておきましょう。

〔問\(\,3\,\)〕
良くある問題なので説明は不要でしょう。
素因数分解して平方数になっていない部分が答えです。

　\(\hspace{10pt}\sqrt{60\,n}\\
=\sqrt{2^2\times \color{red}{3\times 5}\times n}\)

よって\(\,\sqrt{60\,n}\,\)を整数とする最小の自然数\(\,n\,\)は

　\(n=\underline{　15　}\)

⇒　ルートのついた無理数を整数や自然数に変える方法と問題の解き方

整数にする（ルートを外す）だけなら\(\,n\,\)は1つではありません。
最小の自然数だから1つになることを確認しておきましょう。

〔問\(\,4\,\)〕
平行四辺形なので同位角か錯角がポイントになると推測はできるでしょう。
この問題では、二等辺三角形であることも見逃せません。

条件
　\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{∠ADC=50^{\circ}}\,\)
　\(\,\mathrm{ＣＤ=ＣＥ}\,\)
　\(\,\mathrm{∠ACE=20^{\circ}}\,\)
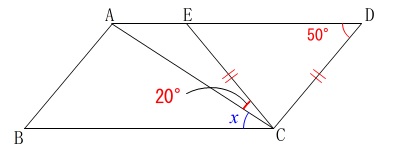\(\,\mathrm{△CED}\,\)は二等辺三角形なので、
　\(\,\mathrm{∠CED=50^{\circ}}\,\)
\(\,\mathrm{ABCD}\,\)は平行四辺形だから錯角は等しいので、
　\(\,\mathrm{∠BCE=50^{\circ}}\,\)
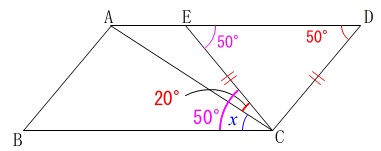よって、
　\(\begin{eqnarray}
\color{blue}{x}+\color{red}{20^{\circ}}&=&\color{magenta}{50^{\circ}}\\
x&=&\underline{　30^{\circ}　}
\end{eqnarray}\)

図形問題では条件を1つでも見落とすと答えまでたどり着けませんよ。

〔問\(\,5\,\)〕
円すいの体積と展開図です。

(1)
体積を\(\,\mathrm{V}\,\)とすると、
底面の半径が\(\,\color{red}{3}\,\)、高さが\(\,\color{blue}{4}\,\)なので

　\(\begin{eqnarray}
\mathrm{V}&=&\frac{1}{3}\times (\pi \,\times \color{red}{3}^2)\times \color{blue}{4}\\
&=&\underline{　12\,\pi　}
\end{eqnarray}\)

(2)
円すいの展開図は扇形と円になります。
側面は扇形ですが、母線と底面の半径の長さによって中心角が変わります。

底面の円周と、側面の弧の長さは等しいので\(\,6\,\pi\,\)です。
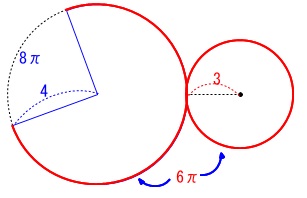半径\(\,4\,\)の円周は\(\,8\,\pi\,\)なので、
扇形の弧の長さは半周の\(\,4\,\pi\,\)より大きいから半円より中心角が大きくなります。

　答え　\(\,\underline{　ア　}\,\)

文章問題の小問集合

　\(\color{blue}{\fbox{　2　}}\)

確率、座標、連立方程式、データの活用の小問集合です。
文章問題ですが、条件をしっかり読み取ればそれほど難しい問題はありません。

〔問\(\,1\,\)〕
袋\(\,\mathrm{A}\,\)と袋\(\,\mathrm{B}\,\)がありますが、関係ありません。

　分母になる\(\,\color{red}{a}\,\)が\(\,1,2,3,4\,\)
　分子になる\(\,\color{blue}{b}\,\)が\(\,5,6,7,8\,\)

このとき、\(\displaystyle \,\frac{\color{blue}{b}}{\color{red}{a}}\,\)が自然数になる確率です。

分母分子の組み合わせは\(\,16\,\)通りありますが、樹形図ですぐに終わります。

ここでは\(\,b\div a\,\)が自然数に組み合わせを書き出しておきます。

自然数になるのは
　分母が\(\,1\,\)のとき分子は\(\,5,6,7,8\,\)の\(\,4\,\)通り
　分母が\(\,2\,\)のとき分子は\(\,6,8\,\)の\(\,2\,\)通り
　分母が\(\,3\,\)のとき分子は\(\,6\,\)の\(\,1\,\)通り
　分母が\(\,4\,\)のとき分子は\(\,8\,\)の\(\,1\,\)通り
で、全部で\(\,8\,\)通りあります。

よって、\(\displaystyle \frac{8}{16}=\underline{　\frac{1}{2}　}\)

〔問\(\,2\,\)〕
放物線を表す関数がありますが比例定数が分かっているので、
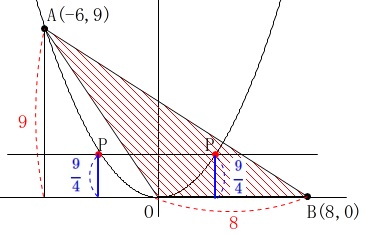
\(\,\mathrm{A}\,\)の座標、\(\,\mathrm{B}\,\)の座標とも具体的に分かります。

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,x=-6\,\)なので、
①の関数に代入すれば\(\,y\,\)座標が分かります。

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{4}\times (-6)^2\\
&=&9
\end{eqnarray}\)

このことから、
　\(\,\mathrm{A\,(\,-6\,,\,9\,)}\,\)

点\(\,\mathrm{B}\,\)は\(\,x\,\)軸上で\(\,x\,\)座標が\(\,8\,\)なので、
　\(\,\mathrm{B\,(\,8\,,\,0\,)}\,\)
※）\(\,x\,\)軸は\(\,y=0\,\)という直線ですよ。
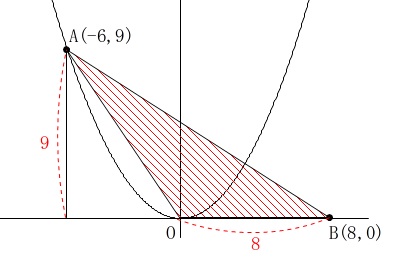このとき\(\,\mathrm{△OAB}\,\)の面積を求める必要はありません。

①上の点\(\,\mathrm{P}\,\)と\(\,\mathrm{O,B}\,\)とでできる\(\,\mathrm{△OPB}\,\)の面積が、
\(\,\mathrm{△OAB}\,\)の\(\displaystyle \,\frac{1}{4}\,\)となる点\(\,\mathrm{P}\,\)を求めるのですが、
底辺\(\,\mathrm{OB}\,\)が共通なので高さが\(\displaystyle \,\frac{1}{4}\,\)となれば良いのです。

つまり、①上の点\(\,\mathrm{P}\,\)の\(\,y\,\)座標が、
点\(\,\mathrm{A}\,\)の\(\,y\,\)座標\(\,\color{red}{9}\,\)の\(\displaystyle \,\frac{1}{4}\,\)
　\(\displaystyle \color{red}{9}\times \frac{1}{4}=\color{blue}{\frac{9}{4}}\)
になれば良いということです。
①の\(\displaystyle \,y=\frac{1}{4}x^2\,\)に\(\displaystyle \,y=\frac{9}{4}\,\)を代入して、

　\(\begin{eqnarray}\displaystyle
\frac{9}{4}&=&\frac{1}{4}\times x^2\\
x^2&=&9\\
x&=&\pm 3
\end{eqnarray}\)

よって求める点\(\,\mathrm{P}\,\)の座標は、
　\(\displaystyle \underline{　\left(\,-3\,,\,\frac{9}{4}\,\right)\,,\,\left(\,3\,,\,\frac{9}{4}\right)　}\)

説明は長いですが、答えまでは\(\,1\,\)分もかかりませんよ。

〔問\(\,3\,\)〕
連立方程式です。
難しく考えなければ難しくありません。笑

お弁当\(\,\color{red}{2}\,\)個とお茶を\(\,\color{blue}{2}\,\)本を買うのは変わりません。

割引クーポンを使うとお弁当を\(\,2\,\)個買うとお茶が\(\,1\,\)本だけ半額になります。
お弁当とお茶をセット割引で買うと、\(\,1\,\)セット\(\,50\,\)円安くなります。

　お弁当\(\,1\,\)個の値段を\(\,x\,\)円、
　お茶\(\,1\,\)本の値段を\(\,y\,\)円
とすると、
割引クーポンを使うと\(\,960\,\)円になるので
　\(\displaystyle \,2x+y+\frac{1}{2}y=960　･･･①\,\)
セット割引を利用すると\(\,2\,\)セット買うことになり\(\,100\,\)円引きになるので
　\(\,2x+2y-100=900　･･･②\,\)

①②を連立して、
　\(\,x=420\,,\,y=80\,\)
（※連立方程式は自分で解いておいて下さい。）

答え　
　\(\,\underline{　お弁当\,1\,個の値段　420\,円　}\,\)
　\(\,\underline{　お茶\,1\,本の値段　80\,円　}\,\)

〔問\(\,4\,\)〕
データの活用の基本用語の確認問題です。

(1)
「適当なものをすべて選びなさい。」なので、
すべて見ておきます。

ア
\(\,1\,\)組の範囲は
　\(\,12-7=5\,\)
\(\,2\,\)組の範囲は
　\(\,14-6=8\,\)
なので\(\,2\,\)組の方が範囲は大きい。
\(\,\color{red}{○}\,\)

イ
相対度数は、
　\(\displaystyle \frac{　各階級の度数　}{　度数合計　}\)
ですが、相対度数は計算する必要はありませんね。

\(\,1\,\)組も\(\,2\,\)組も\(\,11\,\)分以上\(\,12\,\)分未満の階級の度数は同じで\(\,2\,\)です。
しかし、\(\,1\,\)組と\(\,2\,\)組では度数合計が違うので相対度数は違います。
\(\,×\,\)

ウ
\(\,1\,\)組は見る必要はありません。
代表値が同じになるかならないか、です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

平均値は計算があるので後回しにして、笑
\(\,2\,\)組\(\,15\,\)人の中央値は累積度数が\(\,8\,\)になる人がいる階級の階級値なので
　中央値　\(\,9.5\,\)
最頻値は度数の一番多い階級の階級値なので
　最頻値　\(\,10.5\,\)
この2つですでに違うので間違い。
\(\,×\,\)

エ
\(\,1\,\)組の中央値を含む階級は
　\(\,9\,\)分以上\(\,10\,\)分未満の階級
\(\,2\,\)組の中央値を含む階級は
　\(\,9\,\)分以上\(\,10\,\)分未満の階級
なので同じです。
\(\,\color{red}{○}\,\)

オ
\(\,1\,\)組の最頻値は\(\,9.5\,\)
\(\,2\,\)組の最頻値は\(\,\color{red}{10.5}\,\)
なので最頻値が大きいのは\(\,2\,\)組です。
\(\,×\,\)

答え　\(\,\underline{　ア　,　エ　}\,\)

(2)
これは(1)のヒストグラムからちょうど\(\,6\,\)人で区切れるように問題が作られているので、
上位\(\,6\,\)人を抜き出せばすぐに終わります。

記録の良い順に\(\,6\,\)人を選ぶと、
\(\,6\,\)分以上\(\,7\,\)分未満の階級には
　\(\,1\,\)組\(\,\color{red}{0}\,\)人、\(\,2\,\)組\(\,\color{blue}{3}\,\)人
\(\,7\,\)分以上\(\,8\,\)分未満の階級には
　\(\,1\,\)組\(\,\color{red}{2}\,\)人、\(\,2\,\)組\(\,\color{blue}{1}\,\)人
いるので\(\,1\,\)組から\(\,\color{red}{2}\,\)人、\(\,2\,\)組から\(\,\color{blue}{4}\,\)人
選ぶことになります。

　\(\,1\,\)組の代表選手\(\,\color{red}{2}\,\)人の平均値が\(\,7\,\)分\(\,10\,\)秒（\(\,\color{red}{430}\,\)秒）
　\(\,2\,\)組の代表選手\(\,\color{blue}{4}\,\)人の平均値が\(\,6\,\)分\(\,40\,\)秒（\(\,\color{blue}{400}\,\)秒）
なので代表選手\(\,6\,\)人の平均値は、

　\(\begin{eqnarray}\displaystyle
(平均値)&=&\frac{\color{red}{430}\times 2+\color{blue}{400}\times 4}{6}\\
&=&\frac{860+1600}{6}\\
&=&\frac{2460}{6}\\
&=&410　(秒)\\
&=&\underline{　6\,分\,50\,秒　}
\end{eqnarray}\)

分と秒の単位2つを混ぜて計算するのはややこしいので1つの単位で計算しますが、
小さい方の単位、秒に統一して計算したほうが計算しやすいですよ。

規則性問題

　\(\color{blue}{\fbox{　3　}}\)

正方形を重ねて行く規則性問題ですが、縦と横の枚数は同じなので分かり易いです。
推測でも答えが出ますが、一般的に成り立つように文字式でおけるようになっておくと良いですね。

〔問\(\,1\,\)〕
図と表があります。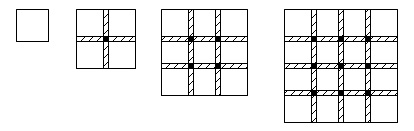図は\(\,4\,\)番目まであるので、表をうめるために\(\,6\,\)番目まで書けば〔問\(\,1\,\)〕は終わりです。
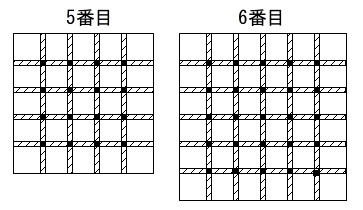数え上げれば答えは出ますが簡単に規則性を見ておきます。

折り紙の枚数は番目の数の平方数になります。
　\(\,1^2\,,\,2^2\,,\,3^2\,,\,4^2\,,\,5^2\,,\cdots\,\)

正方形の\(\,1\,\)辺は、最初の\(\,5\,\)に\(\,4\,\)ずつ増えています。
　\(\,5\,,\,5+4\,,\,5+4\times 2\,,\,5+4\times 3\,,\,\cdots\,\)

重なりの\(\,■\,\)は番目より小さい数の平方数になっています。
　\(\,(1-1)^2\,,\,(2-1)^2\,,\,(3-1)^2\,,\,(4-1)^2\,,\,\cdots\,\)

表をうめると、
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
\,番目 \,& 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
\,枚数\, & 1 & 4 & 9 & 16 & 25 & 36 \\ \hline
\,1\,辺\, & 5 & 9 & 13 & 17 & \color{red}{21} & 25\\ \hline
\,■\, & 0 & 1 & 4 & 9 & 16 & \color{blue}{25}\\ \hline
\end{array}\)

答え　\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　21　}\,\)　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　25　}\,\)

〔問\(\,2\,\)〕

折り紙の枚数は番目の平方数だけ必要です。

　\(\,8\,\)番目の正方形には\(\,8^2=64\,\)枚
　\(\,9\,\)番目の正方形には\(\,9^2=81\,\)枚

この枚数の差だけ貼り合わせることになります。

よって、
　\(\hspace{10pt}81-64\\
=\underline{　17　}　(枚)\,\)

〔問\(\,3\,\)〕
\(\,4\,\)番目の正方形です。
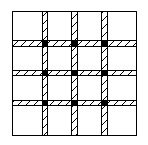\(\,2\,\)枚以上重なっている部分の面積なので斜線部と\(\,■\,\)部分の面積です。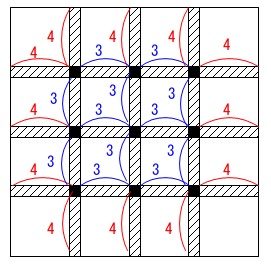
重なり部分の幅は\(\,\mathrm{1\,cm}\,\)なので、
　面積\(\,\color{red}{4}\,\)の長方形が\(\,12\,\)個
　面積\(\,\color{blue}{3}\,\)の長方形が\(\,12\,\)個
　面積\(\,\color{magenta}{1}\,\)の正方形\(\,■\,\)が\(\,9\,\)個
だから、
　\(\hspace{10pt} \color{red}{4}\times 12+\color{blue}{3}\times 12+ \color{magenta}{1}\times 9\\
=48+36+9\\
=\underline{　93　}　(\mathrm{cm^2})\)

〔問\(\,4\,\)〕
正方形や長方形の面積を考える必要はありません。
\(\,1\,\)辺の長さを\(\,n\,\)を用いて表すだけです。

この程度の規則性は簡単に表せるでしょうけど問題にヒントがあります。

バラバラで正方形を\(\,\color{blue}{n}\,\)個並べると\(\,5n\,\)ですが、
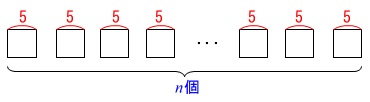\(\,n\,\)番目の正方形では重なり部分は\(\,\color{magenta}{n-1}\,\)個あります。
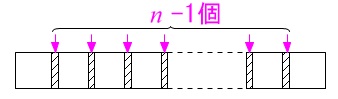重なりの分短くなるので\(\,n\,\)番目の正方形の\(\,1\,\)辺は、

　\(\hspace{10pt}\color{red}{5}\times \color{blue}{n}-(\color{magenta}{n-1})\\
=5n-n+1\\
=\underline{　4n+1　}　(\mathrm{cm})\)

\(\color{black}{\fbox{　3　}}\)はこれで終わりです。
\(\,2\,\)ページに渡っている問題ですが、それほど時間のかかる問題ではありません。

1次関数とグラフの読み取り

　\(\color{blue}{\fbox{　4　}}\)

グラフが与えられていて、\(\,x\,\)軸が時間で\(\,y\,\)軸が距離ですが、
\(\,x=0\,\)が午後\(\,4\,\)時だということさえ気をつけておけば簡単な\(\,1\,\)次関数の基本問題です。
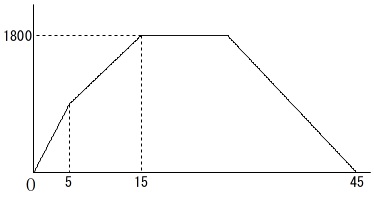歩く速さに変化があるので整理しておきます。

　最初の\(\,5\,\)分間は毎分\(\,\mathrm{180\,m}\,\)
　\(\,5\,\)分から\(\,15\,\)分までは毎分\(\,\mathrm{90\,m}\,\)
　帰りは毎分\(\,\mathrm{100\,m}\,\)

すべての区間での直線の式が求まりますが、問題になっているので順番に見ていきましょう。

〔問\(\,1\,\)〕
午後\(\,4\,\)時\(\,3\,\)分に郵便局の前を通ったということは出発してから\(\,3\,\)分後です。
出発してから\(\,5\,\)分間は分速\(\,\mathrm{180\,m}\,\)で走っているので、
　
　\(\hspace{10pt}180\times 3\\
=\underline{　540　}　(\mathrm{m})\)

〔問\(\,2\,\)〕
歩き始めてから図書館までの関数を求めます。

歩き始めたのは\(\,5\,\)分後で、この時点で家から
　\(\hspace{10pt}180\times 5=900　(\mathrm{m})\)
離れていて、座標で表すと
　\((\,5\,,\,900\,)\)

このあと毎分\(\,\mathrm{90\,m}\,\)で\(\,10\,\)分間歩いて\(\,\mathrm{1800\,m}\,\)離れた図書館についているので、
図書館に着いたときを表す座標は
　\((\,15\,,\,1800\,)\)

この\(\,2\,\)点を通る直線の関数なので、
　\(\begin{eqnarray}\displaystyle
(傾き)&=&(変化の割合)\\
&=&\frac{1800-900}{15-5}\\
&=&\color{red}{90}\,
\end{eqnarray}\)
だから
　\(y=\color{red}{90}x+b\)
とおけて、\(\,2\,\)点を通るのでどちらかを代入して切片を求めます。

\((\,5\,,\,900\,)\)を代入すると、

　\(\begin{eqnarray}
900&=&90\times (5)+b\\
&=&450+b\\
b&=&450
\end{eqnarray}\)

求める\(\,x\,\)と\(\,y\,\)の関係式は

　\(\underline{　y=90x+450　}\)

この問題では\(\,x\,\)の変域（定義域）は求める必要はありませんが、
すべての関数を定義域付きで求めておけばすべての問題がすぐに終わります。

ここでの解説は問題に合わせて進めますが、すべての直線の関数を出すつもりで問題に取り組めばほとんどの関数問題は答えに近づけますよ。

〔問\(\,3\,\)〕
図書館にいた（グラフの横ばいになっている）時間を求めます。

和夫さん（誰でもいいです）は帰りは\(\,\mathrm{1800\,m}\,\)の道のりを分速\(\,\mathrm{100\,m}\,\)で歩いて帰っているので
　\(\hspace{10pt}\displaystyle \frac{1800}{100}=18　(分)\)
かけて\(\,4\,\)時\(\,45\,\)分に家に帰っています。

つまり、図書館を出発したのはその\(\,18\,\)分前の
　\(\,4\,\)時\(\,\color{blue}{27}\,\)分
となります。

図書館に着いたのは\(\,4\,\)時\(\,\color{red}{15}\,\)分なので、図書館にいた時間は、
　
　\(\hspace{10pt}\color{blue}{27}-\color{red}{15}=\underline{　12　}　(分間)\)

今までに分かった座標をグラフに書き込んでみます。
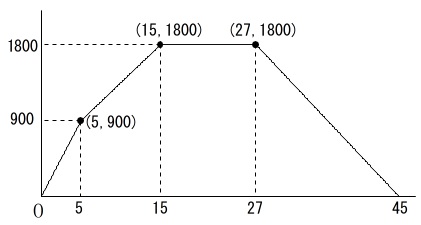\(\,2\,\)点を通る直線の方程式は求められるのですべての関数は出せますね。

〔問\(\,4\,\)〕
妹の美紀さん（誰でもいいです）は\(\,4\,\)時\(\,18\,\)分に家を出発して、
一定の速さで図書館に向かって\(\,4\,\)時\(\,33\,\)分に和夫さんに出会っています。
家を出発して\(\,\color{red}{15}\,\)分後です。

このときの美紀さんの速さを求めます。

\(\,4\,\)時\(\,33\,\)分というと和夫さんが図書館を出発して\(\,6\,\)分後です。

和夫さんは帰りは分速\(\,\mathrm{100\,m}\,\)で歩いているので
　\(100\times 6=600　(\mathrm{m})\)
戻ってきていますので、家からの道のりは
　\(1800-600=\color{blue}{1200}　(\mathrm{m})\)
座標では\(\,(\,33\,,\,1200\,)\,\)になります。
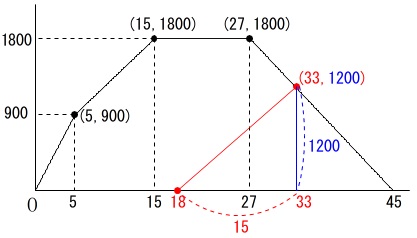この道のりを美紀さんは\(\,\color{red}{15}\,\)分で移動したことになるので求める速さは

　\(\hspace{10pt}\displaystyle \frac{\color{blue}{1200}}{\color{red}{15}}=80　(\mathrm{m}/分)\)

答え　\(\,毎分　\underline{　80　}　(\mathrm{m})\,\)

\(\,4\,\)区間とも直線の式は求まります。
美紀さんの移動を表す直線も求まります。

練習のつもりで求めておくと良いですよ。

円に内接する三角形と相似

　\(\color{blue}{\fbox{　5　}}\)

この問題はシンプルで解法もシンプルなのでサクッと終わらせます。

先ず全体に通じる条件です。

条件
　\(\,\mathrm{AB}\,\)は直径
　\(\,\mathrm{∠BAC}\,\)の二等分線と\(\,\mathrm{BC}\,\)の交点を\(\,\mathrm{D}\,\)
　\(\,\mathrm{OA=5}\,\)
　\(\,\mathrm{AC=3}\,\)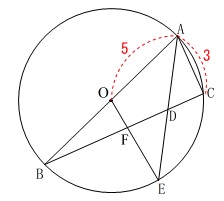

〔問\(\,1\,\)〕
\(\,\mathrm{AB}\,\)は直径なので、
\(\,\mathrm{△ACB}\,\)は\(\,\mathrm{∠ACB=90^{\circ}}\,\)の直角三角形で、
斜辺となる直径が\(\,\mathrm{AB=10}\,\)です。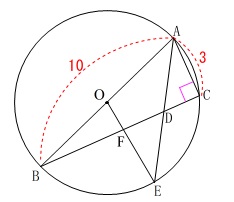三平方の定理から、

　\(\begin{eqnarray}
\mathrm{AC}^2+\mathrm{BC}^2&=&\mathrm{AB}^2\\
3^2+\mathrm{BC}^2&=&10^2\\
\mathrm{BC}^2&=&100-9\\
&=&91\\
\mathrm{BC}&=&\pm \sqrt{91}
\end{eqnarray}\)

線分の長さ\(\,\mathrm{BC}\,＞\,0\,\)なので

　\(\mathrm{BC}=\underline{　\sqrt{91}　(\mathrm{cm})}\)
　
〔問\(\,2\,\)〕

合同の証明です。
図で言えることを示しておきます。

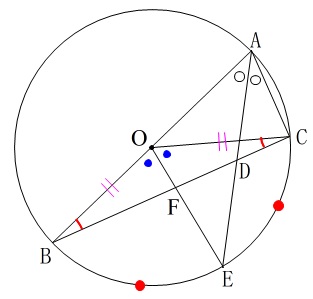
　（証明）
　\(\,\mathrm{△OBF}\,\)　と　\(\,\mathrm{△OCF}\,\)　において
仮定から\(\,\mathrm{AE}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線なので
　\(\,\mathrm{∠BAE=∠EAC}\,\)
円周角が等しいから弧の長さが等しく、
　\(\stackrel{\large{\frown}}{\mbox{BE}} =\stackrel{\large{\frown}}{\mbox{EC}}\)
中心角も等しくなるので、
　\(\,\mathrm{∠BOE=∠EOC}\,\)
これは
　\(\,\mathrm{∠BOF=∠COF　･･･①}\,\)
と同じことを示している。
また、半径は等しいから\(\,\mathrm{△OBC}\,\)は二等辺三角形となるので
　\(\,\mathrm{OB=OC　･･･②}\,\)
このとき底角も等しいので
　\(\,\mathrm{∠OBF=∠OCF　･･･③}\,\)
①②③より
　\(\,1\,\)組の辺とその両端の角がそれぞれ等しい
ので
　\(\,\mathrm{△OBF}\,\)　≡　\(\,\mathrm{△OCF}\,\)
（証明終わり）

\(\,\mathrm{OF}\,\)を共通の辺とみて、
　\(\,2\,\)組の辺とその間の角がそれぞれ等しい
という合同条件でも良いですね。

合同条件が2つも考えられる簡単な証明です。

この程度の証明では円周角と中心角の関係のところは

　\(\,(中心角)=(円周角)\times 2\,\)

を利用して詳しく書いておく方が良いかもしれません。

〔問\(\,3\,\)〕
線分比の問題ですが相似比そのままです。

\(\,\mathrm{△ACG}\,\)と\(\,\mathrm{△ABE}\,\)は最初からる仮定の角の二等分線と、
直径に対する円周角および垂線\(\,\mathrm{CG}\,\)とから相似です。
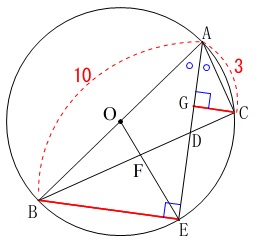よって、
　\(\mathrm{△ACG}\)　∽　\(\,\mathrm{△ABE}\,\)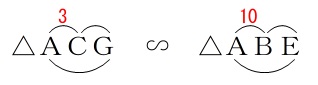相似比から