青森県公立高校入試2019年(平成31年)度の数学問題と解説【後半】

青森県で2019年(平成31年)度に行われた公立高校入試の数学過去問題と解説【後半】です。
第3問が図形、第4問が関数、第5問が規則性の読み取り問題になります。
規則性問題を除けばそれほど考える問題もありませんので手短に解説しておきます。

2019年度青森県公立高校入試数学の問題

問題は青森県で公開してくれています。

⇒　2019年度青森県公立高校入試数学の問題

2019年度青森県公立高校入試数学の解説後半

\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)を前半とし、2019年度青森県公立高校入試数学の続きです。

正方形の回転図形と円柱の動点問題

　\(\color{blue}{\fbox{　3　}}\)

(1)正方形\(\,\mathrm{ABCD}\,\)を\(\,\mathrm{D}\,\)を中心として回転移動しています。
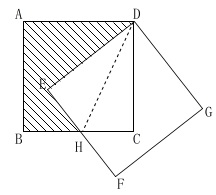正方形の回転なので合同な図形がいくつか出てきます。

ア
　\(\,\mathrm{△DEH}\,\)と\(\,\mathrm{△DCH}\,\)が合同であることの証明です。

図の中で等しい辺や角を書き込んで行けばすぐに合同条件が見つかります。
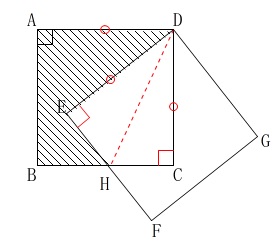他にも合同な三角形はありますが、証明に必要な条件だけにしてあります。

（証明）
　\(\,\mathrm{△DEH}\,\)　と　\(\,\mathrm{△DCH}\,\)　において
共通の辺なので
　\(\mathrm{DH=DH}　･･･①\)
正方形の辺および角は回転しても変わらないので、
　\(\mathrm{DE=DC}　･･･②\)
　\(\,\mathrm{∠DEH=∠DCH=90^{\circ}　･･･③}\,\)
①②③より
　直角三角形の斜辺と他の\(\,1\,\)辺がそれぞれ等しい
ので
　\(\,\mathrm{△DEH}\,\)　≡　\(\,\mathrm{△DCH}\,\)
（証明終わり）

イ
方程式を立てて辺の長さを求めますが、
　\(\,\mathrm{BH:HC=2:3}\,\)
なので、求める正方形の\(\,1\,\)辺を\(\,5x\,\)とすると計算がしやすいです。
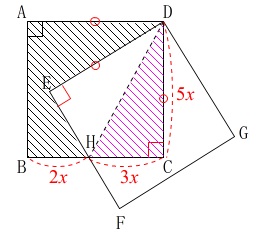正方形の\(\,1\,\)辺を\(\,\color{red}{5x}\,\)とすると、
　\(\,\mathrm{BH:HC=2:3}\,\)
なので
　\(\,\mathrm{BH}=2x\,,\,\mathrm{CH}=3x\,\)
とおけるので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△DCH}}&=&\frac{1}{2}\times \mathrm{CH}\times \mathrm{DC}\\
&=&\frac{1}{2}\times 3x\times 5x\\
&=&\color{magenta}{\frac{15}{2}x^2}
\end{eqnarray}\)

\(\,\mathrm{△DEH}\,\)と\(\,\mathrm{△DCH}\,\)は合同なので面積も等しいから、

　\(\begin{eqnarray}\displaystyle
　(四角形\mathrm{DEHC})&=&2\times \color{magenta}{\frac{15}{2}x^2}\\
&=&15x^2
\end{eqnarray}\)

斜線部分の面積が\(\,\mathrm{20\,cm^2}\,\)であることから
　\(\,\mathrm{(正方形ABCD)-(四角形DEHC)=20}\,\)
だから

　\(\begin{eqnarray}
(5x)^2-15x^2&=&20\\
10x^2&=&20\\
x^2&=&2
\end{eqnarray}\)

\(\,x\,＞\,0\,\)なので\(\,x=\sqrt{2}\,\)

よって正方形の\(\,1\,\)辺は
　\(\,5x=\underline{　5\sqrt{2}　}\,\)

求めるのは\(\,x\,\)ではなく\(\,5x\,\)ですので間違えないようにして下さい。
もちろん正方形の\(\,1\,\)辺を\(\,x\,\)とおいても同じ答えが出ます。

(1)はそれほど考えなかったと思いますが、差が出るのは(2)です。
\(\,2\,\)点が空間で動いている問題なので取り組みにくかった人も多いのではないでしょうか。

何故難しく見えるか？
理由は簡単です。

空間のまま考えようとしているから。

(2)
ア
これは\(\,2\,\)点\(\,\mathrm{P,Q}\,\)とは関係ありません。

底面の半径が\(\,5\,\)で、高さが\(\,10\,\)の円柱の表面積です。
円柱の展開図を書き出します。
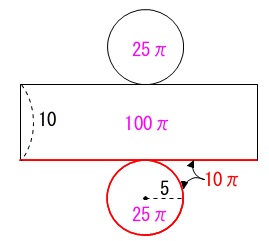底面の円周と側面の長方形の横の長さは等しくなります。

求める表面積は

　\(\hspace{10pt}\pi\times (5)^2\times 2+10\,\pi\times 10\\
=50\,\pi+100\,\pi\\
=\underline{　150\,\pi　}　(\mathrm{cm^2})\)

イ
円\(\,\mathrm{O}\,\)上を\(\,\mathrm{P}\,\)は動きます。

点\(\,\mathrm{P}\,\)は\(\,30\,\)秒で\(\,1\,\)周するので、
\(\,5\,\)秒だと、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AOP}&=&360°\times \frac{5}{30}\\
&=&\underline{　60^{\circ}　}\end{eqnarray}\)
回転します。
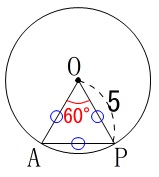このとき\(\,\mathrm{△AOP}\,\)は正三角形になるので、
　\(\,\mathrm{AP=5}\,\)
点\(\,\mathrm{B}\,\)は動かないので\(\,\mathrm{AB}\,\)と\(\,\mathrm{AP}\,\)が垂直になります。
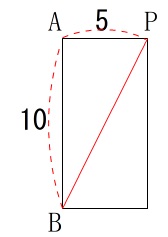三平方の定理を利用して、

　\(\begin{eqnarray}
\mathrm{PB^2}&=&\mathrm{AP^2+AB^2}\\
&=&5^2+10^2\\
&=&25+125\\
&=&125\\
\mathrm{PB}&=&\pm 5\sqrt{5}
\end{eqnarray}\)

\(\,\mathrm{PB\,＞\,0}\,\)より\(\,\mathrm{PB}=\underline{　5\sqrt{5}　(\mathrm{cm})}\,\)

ウ
\(\,\mathrm{OP}\,\)と\(\,\mathrm{O’Q}\,\)が平行になるときを考えます。

しかし、\(\,\mathrm{OP}\,\)と\(\,\mathrm{OQ}\,\)は同じ平面上にないので考えにくいです。
同じ平面で考えましょう。

円柱を真上から見れば、ねじれているようには見えません。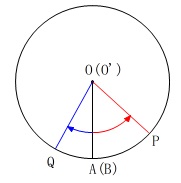
ここで、点\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)から反時計回りに\(\,30\,\)秒で\(\,360°\,\)まわるので、
　\(\hspace{10pt}(毎秒)　360^{\circ}\div 30=12^{\circ}　\)
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{A}\,\)から時計回りに\(\,45\,\)秒で\(\,360°\,\)まわるので、
　\(\hspace{10pt}(毎秒)　360^{\circ}\div 45=8^{\circ}\)
回転することになります。

最初に\(\,\mathrm{OP}\,\)と\(\,\mathrm{O’Q}\,\)が平行になるのは、
　\(\,\mathrm{∠POQ=180^{\circ}}\,\)
となるときで、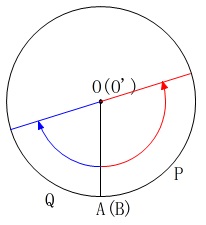
　\(\begin{eqnarray}
12x+8x&=&180\\
20x&=&180\\
x&=&\underline{　9　}　(秒後)
\end{eqnarray}\)

次に\(\,\mathrm{OP}\,\)と\(\,\mathrm{O’Q}\,\)が平行になるのは\(\,\mathrm{OP}\,\)と\(\,\mathrm{O’Q}\,\)が重なって見えるときです。
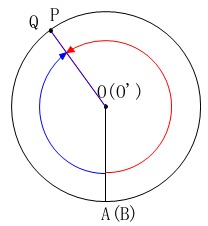つまり、\(\,\mathrm{∠AOP+∠AOQ=180^{\circ}}\,\)となるときで、
\(\,\mathrm{∠POQ}\,\)のつくる角度が毎秒\(\,20^{\circ}\,\)増えることから

　\(\begin{eqnarray}
20x&=&360\\
x&=&\underline{　18　}　(秒後)
\end{eqnarray}\)

これで終わりではありません。
点\(\,\mathrm{P}\,\)が円\(\,\mathrm{O}\,\)の周上を\(\,1\,\)周するのに\(\,30\,\)秒かかりますので、
もう一度平行となる場合があります。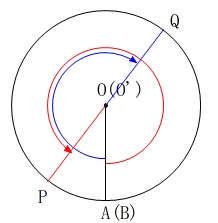周期から見ても\(\,27\,\)秒後と分かりますが、
　\(\,\mathrm{∠AOP+∠AOQ=360^{\circ}+180^{\circ}}\,\)
となるときで、
　\(\begin{eqnarray}
20x&=&360+180\\
x&=&\underline{　27　}　(秒後)
\end{eqnarray}\)

答え　\(\,\underline{　9\,,\,18\,,\,27　} (秒後)\,\)

弧の長さや方程式を利用して求める方法もありますが、
どのような場合があるかを探す方法で求めておきました。

問題に、
　『出発時の重なりは考えないものとする』
と重なるときも平行であることがヒントとして書いてあります。

こういう一言は何故書いてあるのか少しだけでも考えておくと良いですよ。
必要無いことは問題には普通書いていないものです。

エ
線分\(\,\mathrm{PQ}\,\)の長さの変域です。

これは簡単で、重なったときが最小で、反対側に平行になったときが最大になります。

最小になるのは線分\(\,\mathrm{AB}\,\)と同じで\(\,\color{blue}{10}\,\)です。
　
最大になるのは\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)が反対側で\(\,\mathrm{P,O,Q}\,\)が平行になるときなので、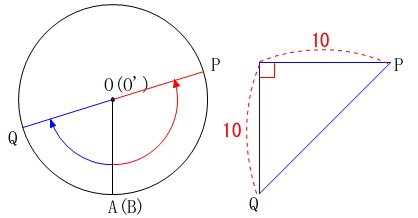
　\(\begin{eqnarray}
\mathrm{PB^2}&=&10^2+10^2\\
&=&200\\
\mathrm{PB}&=&\color{red}{10\sqrt{2}}　(\mathrm{PB}\,＞\,0)
\end{eqnarray}\)

よって
　\(\underline{　10　}\,≦\,\mathrm{PQ}\,≦\,\underline{　10\sqrt{2}　}\)

この程度の問題に時間をかける必要もないので先に進めます。

関数（放物線と双曲線と直線）

　\(\color{blue}{\fbox{　4　}}\)

グラフを見ると複雑そうに見えますが、気をつける問題は(3)だけです。

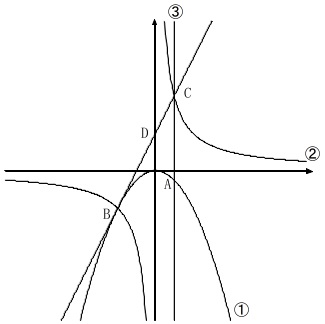問題に書いてある条件がありますので見ておきましょう。

　①:\(\,y=ax^2\)
　②:\(\,\displaystyle y=\frac{16}{x}\,\)
　③:\(\,x=2\,\)
　\(\,\mathrm{A}\,\)は①と③の交点
　\(\,\mathrm{B}\,\)は①と②の交点で\(\,x\,\)座標が\(\,-4\,\)

後は座標上に示していある通りです。
③の直線が\(\,x=2\,\)なので、
　\(\,\mathrm{A}\,\)も\(\,\mathrm{C}\,\)も\(\,x\,\)座標が\(\,2\,\)
だということを見逃さないようにしましょう。

(1)
①の関数の比例定数\(\,a\,\)を求めます。

①は\(\,\mathrm{B}\,\)を通ります。
\(\,\mathrm{B}\,\)は②上の点でもあり\(\,x\,\)座標が\(\,4\,\)なので

　\(\begin{eqnarray}\displaystyle
y&=&\frac{16}{-4}\\
&=&-4
\end{eqnarray}\)

つまり、\(\,\mathrm{B}\,\)の座標は\(\,(\,-4\,,\,-4\,)\,\)で①は\(\,\mathrm{B}\,\)を通るので、

　\(\begin{eqnarray}\displaystyle
-4&=&a\times (-4)^2\\
-4&=&16a\\
a&=&\underline{　-\frac{1}{4}　}
\end{eqnarray}\)

①は決まりました。
　\(\displaystyle y=-\frac{1}{4}\,x^2\)　
このとき\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,2\,\)だから
　\(\mathrm{A}\,(\,2\,,\,-1\,)\,\)
また、\(\,\mathrm{C}\,\)は③上の点で\(\,x\,\)座標が\(\,2\,\)だから　
　\(\,\mathrm{C\,(\,2\,,\,8\,)}\,\)

分かったことをグラフ上に示しておきます。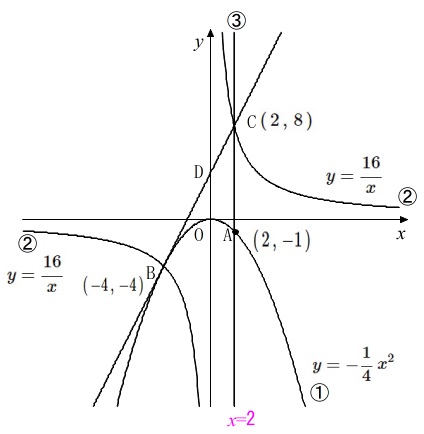ここまでくれば\(\color{black}{\fbox{　4　}}\)は終わったようなものです。

(2)
直線\(\,\mathrm{BC}\,\)は\(\,2\,\)点
　\(\,\mathrm{B}\,(\,-4\,,\,-4\,)\,\)
　\(\,\mathrm{C\,(\,2\,,\,8\,)}\,\)
を通るので、傾き（変化の割合に等しい）が
　\(\hspace{10pt}\displaystyle \frac{8-(-4)}{2-(-4)}=\color{red}{2}\)
だから、\(\,y=\color{red}{2}x+b\,\)とおけて\(\,\mathrm{B}\,\)と\(\,\mathrm{C}\,\)を通るのでどちらかを代入して、
　\(\begin{eqnarray}
8&=&\color{red}{2}\times (2)+b\\
b&=&4
\end{eqnarray}\)

よって、\(\underline{　y=2x+4　}\)

また\(\,2\,\)点を通る直線を直接求める方法を知っている人は
　\(\begin{eqnarray}\displaystyle
y-8&=&\frac{8-(-4)}{2-(-4)}(x-2)\\
y&=&2x+4
\end{eqnarray}\)
とかっこよく求めても良いですが、時間は大して変わりません。笑

(3)
①の関数は求めてあります。
問題は\(\displaystyle \,y=-\frac{1}{4}x^2\,\)の\(\,x\,\)の変域が
　\(\,n\,≦\,x\,≦\,4\,\)
のとき、\(\,y\,\)の変域が
　\(\,-4\,≦\,y\,≦\,0\,\)
となるときの\(\,n\,\)を整数値で求めます。

グラフを見ればすぐに分かりますが、
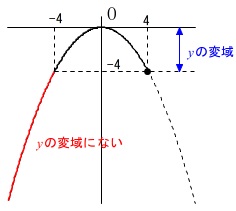赤い部分を含むと最小値が\(\,-4\,\)より小さくなり、
\(\,x=0\,\)は\(\,x\,\)の変域に入っていないと最大値が\(\,0\,\)にはなりません。

だから\(\,n\,\)は
　\(\,-4\,\)以上で\(\,0\,\)以下
でなければ\(\,y\,\)の変域が\(\,\color{blue}{-4}\,≦\,y\,≦\,\color{blue}{0}\,\)となりません。

答え　\(\,n=\underline{　-4\,,\,-3\,,\,-2\,,\,-1\,,\,0　}\,\)

(4)
①上の点\(\,\mathrm{P}\,\)とでつくる\(\,\mathrm{△ACP}\,\)の面積が、
\(\,\mathrm{△ACD}\,\)の面積の\(\,5\,\)倍になるときの\(\,\mathrm{P}\,\)の座標を求めます。

底辺\(\,\mathrm{AC}\,\)を共通にしているので簡単です。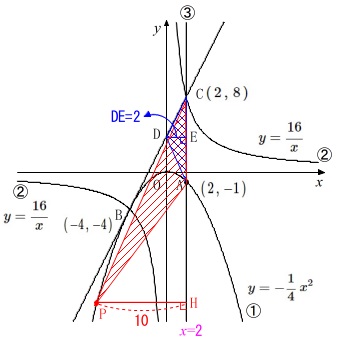具体的な面積を求める必要もありません。
底辺\(\,\mathrm{AC}\,\)は共通なので同じ長さだから、
　\(\,\mathrm{△ACP}\,\)の高さとなる\(\,\mathrm{\color{red}{PH}}\,\)が
　\(\,\mathrm{△ACD}\,\)の高さとなる\(\,\mathrm{\color{blue}{DE}}\,\)の\(\,5\,\)倍
となれば良いだけです。

点\(\,\mathrm{E}\,\)は③上にあるので\(\,x\,\)座標が\(\,2\,\)で、
\(\,\mathrm{D}\,\)は\(\,y\,\)軸\(\,(x=0)\,\)上の点なので
　\(\,\mathrm{\color{blue}{DE}=\color{blue}{2}}\,\)

この\(\,5\,\)倍なので
　\(\,\mathrm{\color{red}{PH}=\color{red}{10}}\,\)

点\(\,\mathrm{H}\,\)も③上にあるので\(\,x\,\)座標が\(\,2\,\)だから、
　\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,-8\,\)
点\(\,\mathrm{P}\,\)の\(\,y\,\)座標は①上の点であることから
　\(\begin{eqnarray}\displaystyle
y&=&-\frac{1}{4}\,(-8)^2\\
&=&-16
\end{eqnarray}\)

よって求める点\(\,\mathrm{P}\,\)の座標は
　\(\hspace{10pt}\displaystyle \underline{　(\,-8\,,\,-16\,)　}\)

「座標」を聞かれているので\(\,x,y\,\)座標の両方ですよ。

\(\,\mathrm{△ACP}\,\)が\(\,\mathrm{△ACD}\,\)の\(\,5\,\)倍になるのは、
\(\,\mathrm{P}\,\)の座標を設定して求めると\(\,x\,\)座標が\(\,12\,\)のときもありますが、
問題に「点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は負である。」と書いてあるので答えにはなりません。

規則性と文字式

　\(\color{green}{\fbox{　5　}}\)

文字数はそれほど多くはありませんが規則性を見抜いて整理するのは、
慣れていない人にはできないか、できても時間がかかる問題です。

ですので、簡単に済ませてます。笑

(1)から解いて行けば分かるように問題が導いてくれますが、手順をまとめておきます。

先生\(\,4\,\)人と生徒\(\,90\,\)人の記事を\(\,2\,\)ずつ\(\,1\,\)ページに配置し、
集合写真と編集後記を\(\,1\,\)ページ加え合計\(\,48\,\)ページの文集を作ります。

つまり、\(\,96\,\)個の記事を\(\,2\,\)個ずつ\(\,1\,\)ページに配置して\(\,48\,\)ページの文集を作ります。

ややこしいのは、順番に両面に印刷して行くのではなく、重ねて折り曲げて真ん中を閉じたときにページ順になるように配置するということです。

両面で\(\,8\,\)個の記事を配置するので用紙は
　\(\,96\div 8=12　(枚)\,\)
となります。
※このことから(4)では何枚目か？という問がありますが、\(\,12\,\)より大きい数字は出てきません。

紙を\(\,12\,\)枚用意して折り曲げて順に番号だけ書いていけばある程度は解ける問題ですけど、
さすがに試験中はできないでしょうからイメージして下さい。笑
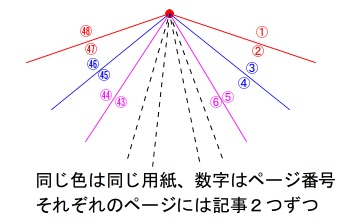綴じた文集を真上から見た状態です。

(1)
ページ番号だけなので簡単です。
\(\,1\,\)ページには\(\,2\,\)個の記事が配置されます。

\(\,1\,\)組\(\,30\,\)番の人は先生も含めると\(\,34\,\)個目の記事だから

　\(34\div \color{red}{2}=\underline{　17　}　(ページ)\)　

\(\,3\,\)組\(\,1\,\)番の人は先生も含めて\(\,2\,\)組の\(\,30\,\)人目が終わったページの次のページになります。
\(\,2\,\)組の\(\,30\,\)番の人は先生と\(\,1\,\)組も含め\(\,64\,\)個目の記事なので\(\,32\,\)ページの下段になります。

よって\(\,3\,\)組\(\,1\,\)番の人は次のページで
　\(\underline{　33　}　(ページ)\)

(2)
\(\,2\,\)組だけに着目してはややこしくなります。

先生から始まり\(\,1\,\)組\(\,2\,\)組と通し番号が打ってあるとすると、
\(\,2\,\)組の\(\,1\,\)番は先生\(\,4\,\)人と\(\,1\,\)組\(\,30\,\)人の次から始まるので、
\(\,35\,\)番からとなります。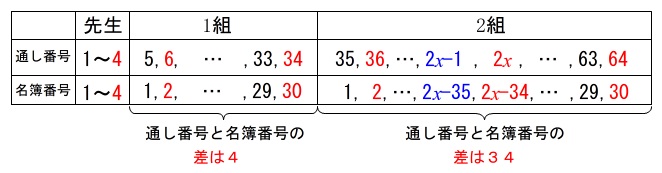※赤字の偶数番号は下段の記事になります。

\(\,x\,\)ページの下段の人の番号は通し番号では\(\,\color{red}{2x}\,\)ですが、
\(\,1\,\)組の\(\,30\,\)番までで\(\,34\,\)記事分あるので、
\(\,x\,\)ページの下段で\(\,2\,\)組の人の名簿番号は
　\(\color{black}{\fbox{　ア　}}\)　\(\underline{　2x-34　}\)

(3)
この問題は記事番号ではなくて、ページ番号についての問題です。
図\(\,2\,\)のページ番号を見ていくと規則性が見えてきます。

裏のページ数を見ていくと、
左は
　\(\,47,45,43,\cdots \,\)
とページ番号が\(\,2\,\)ずつ減っていき、
右が
　\(\,2,4,6\,\cdots \,2n,\cdots\,\)
と\(\,2\,\)ずつ増えていきます。

表も裏もとなりのページ数合計は\(\,\color{blue}{49}\,\)なので、
\(\,n\,\)枚目の裏は、
　右のページは\(\,\color{red}{2n}\,\)
　左のページは\(\,\color{blue}{49}-\color{red}{2n}\,\)

答え　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　49-2n　}\,\)　\(\color{black}{\fbox{　ウ　}}\)　\(\,\underline{　2n　}\,\)
　
(4)
(2)と(3)を利用して考えて、というのが問題を作成された方の意図でしょう。

ただし、(3)では裏の場合しか見ていないので表の場合を自分で探る必要があります。

ここでは(2)(3)がない場合ならどうするかを先に解説します。
分かるだけ具体的に書き出して規則性を見つける練習にしてみましょう。

表と裏で規則性が少し違うので別に考えます。

(1)で解説したように番号を通しで考えると、
　\(\,2\,\)組は記事番号が\(\,\color{red}{35}\,\)～\(\,\color{red}{64}\,\)、
　用紙は全部で\(\,\color{red}{12}\,\)枚、
ということは思いだしておいて下さい。

表の記事配列で下段の記事番号で並べると、
　\(\begin{array}{|c|c|c|c|} \hline
\,表の順番\,&\,左(a)\,&\,右(b)\,&\,差\,\\ \hline
\,表\,1\,枚目\,&\,2\,&\,96\,&\,-94\,\\ \hline
\,表\,2\,枚目\,&\,6\,&\,92\,&\,-86\,\\ \hline
\,表\,3\,枚目\,&\,10\,&\,88\,&\,-78\,\\ \hline
\,表\,4\,枚目\,&\,14\,&\,84\,&\,-70\,\\ \hline
\,表\,5\,枚目\,&\,18\,&\,80\,&\,-62\,\\ \hline
\,表\,6\,枚目\,&\,22\,&\,76\,&\,-54\,\\ \hline
\,表\,7\,枚目\,&\,26\,&\,72\,&\,-46\,\\ \hline
\,表\,8\,枚目\,&\,30\,&\,68\,&\,-38\,\\ \hline
\,表\,9\,枚目\,&\,34\,&\,\color{red}{64}\,&\,-30\,\\ \hline
\,表\,10\,枚目\,&\,\color{red}{38}\,&\,\color{red}{60}\,&\,-22\,\\ \hline
\,表\,11\,枚目\,&\,\color{red}{42}\,&\,\color{red}{56}\,&\,-14\,\\ \hline
\,表\,12\,枚目\,&\,\color{red}{46}\,&\,\color{red}{52}\,&\,-6\,\\ \hline
\end{array}\)

用紙は\(\,12\,\)枚しかないのでこれで終わりです。
赤字は\(\,2\,\)組の記事ですが\(\,a-b=10\,\)となる用紙は\(\,2\,\)組でなくてもありません。

もっと先まで行くと\(\,n=14\,\)のときになりますが用紙は\(\,12\,\)枚しかないのでありません。
後で数式で確認してみましょう。

裏の記事配列で下段の記事番号で並べると、
　\(\begin{array}{|c|c|c|c|} \hline
\,裏の順番\,&\,左(a)\,&\,右(b)\,&\,差\,\\ \hline
\,裏\,1\,枚目\,&\,94\,&\,4\,&\,90\,\\ \hline
\,裏\,2\,枚目\,&\,90\,&\,8\,&\,82\,\\ \hline
\,裏\,3\,枚目\,&\,86\,&\,12\,&\,74\,\\ \hline
\,裏\,4\,枚目\,&\,82\,&\,16\,&\,66\,\\ \hline
\,裏\,5\,枚目\,&\,78\,&\,20\,&\,58\,\\ \hline
\,裏\,6\,枚目\,&\,74\,&\,24\,&\,50\,\\ \hline
\,裏\,7\,枚目\,&\,70\,&\,28\,&\,42\,\\ \hline
\,裏\,8\,枚目\,&\,66\,&\,32\,&\,34\,\\ \hline
\,裏\,9\,枚目\,&\,\color{red}{62}\,&\,\color{red}{36}\,&\,26\,\\ \hline
\,裏\,10\,枚目\,&\,\color{red}{58}\,&\,\color{red}{40}\,&\,18\,\\ \hline
\,裏\,11\,枚目\,&\,\color{red}{54}\,&\,\color{red}{44}\,&\,\color{blue}{10}\,\\ \hline
\,裏\,12\,枚目\,&\,\color{red}{50}\,&\,\color{red}{48}\,&\,2\,\\ \hline
\end{array}\)

\(\,\color{red}{2}\,\)組の記事どうしの差が\(\,a-b=\color{blue}{10}\,\)の用紙がありました。

答え　\(\,\underline{　11\,枚目の裏　}\,\)

順番に調べて行くと答えがほぼ最後に出てくる、という問題です。笑
　

(2)(3)を利用して文字式で解いて見ます。

(2)から\(\,x\,\)ページの\(\,2\,\)組の下段の記事番号は\(\,2x-34\,\)です。

(3)から\(\,n\,\)枚目の裏は、
　左のページが\(\,\color{red}{49-2n}\,\)
　右のページが\(\,\color{blue}{2n}\,\)
なので記事番号を\(\,n\,\)を用いて表すと、
左のページの下段記事番号は
　\(\begin{eqnarray}
a&=&2(\color{red}{49-2n})-34\\
&=&94-4n-34\\
&=&60-4n\end{eqnarray}\)
右のページの下段記事番号は
　\(\begin{eqnarray}
b&=&2(\color{blue}{2n})-34\\
&=&4n-34\end{eqnarray}\)

よって、\(\,a-b=10\,\)となるときがあるとすれば、
　\(\begin{eqnarray}
(60-4n)-(4n-34)&=&10\\
60-4n-4n+34&=&10\\
-8n&=&-88\\
n&=&11
\end{eqnarray}\)

で答えは\(\,\underline{　11\,枚目の裏　}\,\)とでますが、表を見ていません。

裏のときと同じように、
（\(\,2\,\)組の記事番号\(\,35～64\,\)までの間では）
(2)から\(\,x\,\)ページの下段の記事番号は\(\,(2x-34)\,\)です。

(3)と同じように\(\,n\,\)枚目の表は、
　左のページが\(\,\color{red}{2n-1}\,\)
　右のページが\(\,\color{blue}{50-2n}\,\)
なので記事番号を\(\,n\,\)を用いて表すと、
左のページの下段記事番号は
　\(\begin{eqnarray}
a&=&2(\color{red}{2n-1})-34\\
&=&4n-2-34\\
&=&4n-36
\end{eqnarray}\)
右のページの下段記事番号は
　\(\begin{eqnarray}
a&=&2(\color{blue}{50-2n})-34\\
&=&100-4n-34\\
&=&66-4n
\end{eqnarray}\)