青森県公立高校入試2019年(平成31年)度の数学問題と解説

青森県で2019年(平成31年度)に行われた公立高校入試の数学の問題と解説です。
問題は問1から問5までの大問がありますが、配点は問1に半分近くがあるので目標得点を決めたら時間配分に注意して受験しましょう。
満点を狙うのであれば、ポイントは手を動かすことです。

問題は青森県で公開してくれています。

⇒　2019年青森県公立高校入試数学問題

小問集合（式の計算や方程式）

　\(\color{blue}{\fbox{　1　}}\)

基本問題が並んだ小問集合です。
配点が\(\,43\,\)点ありますので素早く、確実に得点しておきましょう。

(1)
ア
　\(\hspace{10pt}-8+6\\
=\underline{　-2　}\)

正の数負の数の計算なので問題ないでしょう。
数直線上で考えれば良いです。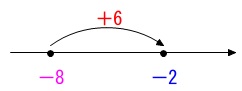

イ
小数は分数にして、割り算は逆数のかけ算です。

　\(\hspace{10pt}\displaystyle (-0.5)\div \frac{2}{7}\\
\displaystyle =\left(-\frac{1}{2}\right)\times \frac{7}{2}\\
\displaystyle =\underline{　-\frac{7}{4}　}\)

符号には注意しておきましょう。

ウ
文字式の引き算をしろということです。
同類項だけを引く計算を続ければいいですよ。

　\(\hspace{14pt}a+3b-2\\
\underline{-)\hspace{2pt}a-\hspace{4pt}b+4}\\
\hspace{30pt}\underline{　4b-6　}\)

引いているので下の式の符号は反対になって上の式に加わります。

普通に文字式の引き算をした方が慣れているのではないでしょうか。

　\(\hspace{10pt}a+3b-2-(a-b+4)\\
=a+3b-2-a+b-4\\
=\underline{　4b-6　}\)

エ
文字式を展開して引き算するだけです。

　\(\hspace{10pt}(x-2)^2-(x-1)(x+4)\\
=x^2-4x+4-(x^2+3x-4)\\
=x^2-4x+4\color{red}{-x^2-3x+4}\\
=\underline{　-7x+8　}\)

公式を利用して展開していますが、一つひとつ展開しても良いです。
見直しは公式利用せず計算してみると良いですね。

\(\,3\,\)行目の（かっこ）を外す\(\,1\,\)行は飛ばさない方がミスが確実に減ります。
下手に暗算するより早いです。笑

オ
無理数の有理化と加減です。

　\(\hspace{10pt}\displaystyle \sqrt{3}-\frac{9}{\sqrt{3}}-\sqrt{12}\\
\displaystyle =\sqrt{3}-\frac{9\sqrt{3}}{3}-2\sqrt{3}\\
\displaystyle =\sqrt{3}-3\sqrt{3}-2\sqrt{3}\\
=\underline{　-4\sqrt{3}　}\)

無理数のルートの中が同じ場合はルートの前の整数部分で足し算引き算ができます。

⇒　近似値とは？ルートのついた無理数の分母の有理化と近似値の使い方

有理化が不安という人は必ず復習しておきましょう。
計算問題だけではなく、問題全体で何点捨てることになるか分かりませんよ。

(2)
関係式を不等式で表します。

　大人\(\,2\,\)人の料金が\(\,\color{red}{2a}\,\)円
　子ども\(\,3\,\)人の料金が\(\,\color{blue}{3b}\,\)円
　合計が\(\,\color{magenta}{2000円以下}\,\)

なので

　\(\underline{　2a+3b\,≦\,2000　}\)

日本語の通りに組み立てれば良いだけです。

(3)
代入は文字式を簡単にした後です。

　\(\hspace{10pt}6\,a\,b^2\times (-a)^2\\
=6\,a\,b^2\times a^2\\
=6\,a^3\,b^2\\
=6\times(-2)^3\times (-1)^2\\
=6\times (-8)\times 1\\
=\underline{　-48　}\)

代入するときは正の数でも負の数でも（かっこ）をつけておくと符号ミスが減ります。

(4)
\(\,2\,\)次方程式を解くときは因数分解を先に試して見ると良いですが、
ここでは簡単には因数分解ができないので解の公式です。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

　\(\hspace{10pt}x^2+x-3=0\)

解の公式より

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-1\pm \sqrt{1^2-4\times 1\times (-3)}}{2}\\
&=&\frac{-1\pm \sqrt{1+12}}{2}\\
&=&\underline{　\frac{-1\pm \sqrt{13}}{2}　}
\end{eqnarray}\)

⇒　２次方程式を解の公式で解く問題の見分け方と例題

因数分解できる問題も多いので確認しておいた方が良いですよ。

確率や角度の基本小問集合

(5)
「少なくとも」とあるので、反対を考えれば良いのですがここではまともに場合を出しておきます。

少なくとも\(\,1\,\)人はあたりを引く場合は、
　\(\,\mathrm{A}\,\)が当たりで\(\,\mathrm{B}\,\)も当たり
　\(\,\mathrm{A}\,\)が当たりで\(\,\mathrm{B}\,\)が外れ
　\(\,\mathrm{A}\,\)が外れで\(\,\mathrm{B}\,\)が当たり
の\(\,3\,\)通りがあるのでそれぞれの確率を足します。

しかし、ずべての場合を書き出した方がはやいですね。
\(\,1\,\)から\(\,5\,\)までの数字を考え、
\(\,1,2,3\,\)までが当たりで\(\,\color{red}{4},\color{red}{5}\,\)が外れだとします。
ここでは表にしますが、樹形図の方がはやいですよ。

　\(\begin{array}{|c|c|c|} \hline
　\mathrm{A}　&　\mathrm{B}　& 　1人は当たる　\\ \hline
　1　&　2　&　○　\\ \hline
　1　&　3　&　○　\\ \hline
　1　&　\color{red}{4}　&　○　\\ \hline
　1　&　\color{red}{5}　&　○　\\ \hline
　2　&　1　&　○　\\ \hline
　2　&　3　&　○　\\ \hline
　2　&　\color{red}{4}　&　○　\\ \hline
　2　&　\color{red}{5}　&　○　\\ \hline
　3　&　1　&　○　\\ \hline
　3　&　2　&　○　\\ \hline
　3　&　\color{red}{4}　&　○　\\ \hline
　3　&　\color{red}{5}　&　○　\\ \hline
　\color{red}{4}　&　1　&　○　\\ \hline
　\color{red}{4}　&　2　&　○　\\ \hline
　\color{red}{4}　&　3　&　○　\\ \hline
　\color{red}{4}　&　\color{red}{5}　&　\color{red}{×}　\\ \hline
　\color{red}{5}　&　1　&　○　\\ \hline
　\color{red}{5}　&　2　&　○　\\ \hline
　\color{red}{5}　&　3　&　○　\\ \hline
　\color{red}{5}　&　\color{red}{4}　&　\color{red}{×}　\\ \hline
\end{array}\)

答え　\(\displaystyle \frac{18}{20}= \underline{　\frac{9}{10}　}\)

\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)が\(\,\color{red}{4}\,\)と\(\,\color{red}{5}\,\)を引いたときだけが「少なくとも\(\,1\,\)人はあたる」ではないので、逆の方がはやいでしょう。

確率はすべての場合の確率が\(\,1\,\)（何かは起こる）だから、
余事象の確率を\(\,1\,\)からひいて

　\(\hspace{10pt}\displaystyle 1-\frac{2}{20}\\
\displaystyle =\frac{18}{20}\\
\displaystyle =\underline{　\frac{9}{10}　}\)

残念ながら余事象という言葉が中学生にはありません。
が、考え方は使って良いですよ。

(6)
水を移動させたときの比例式を解くだけです。

　\(\,\mathrm{42\,L}\,\)ずつ入った容器\(\,\mathrm{A}\,\)、\(\,\mathrm{B}\,\)があって、
　\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)に\(\,x\,\mathrm{L}\,\,\)移したら\(\,\color{red}{2:5}\,\)になった。
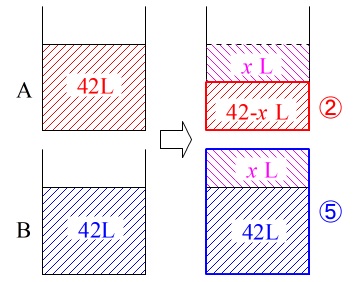移した水の量を文字\(\,x\,\)を使って比例式を立てて解くと、

移した後、
　\(\,\mathrm{A}\,\)は\(\,42-x\,\)
　\(\,\mathrm{B}\,\)は\(\,42+x\,\)
なので
　\(\begin{eqnarray}
(42-x):(42+x)&=&2:5\\
2(42+x)&=&5(42-x)\\
84+2x&=&210-5x\\
7x&=&126\\
x&=&\underline{　18　}　(\mathrm{L})
\end{eqnarray}\)

(7)
角度を求めます。
具体的な数値は少ないですが文字を使えば簡単に求まります。

条件
　図の\(\,\mathrm{∠B}\,\)の二等分線と\(\,\mathrm{∠ACE}\,\)の二等分線の交点を\(\,\mathrm{D}\,\)
2等分された角の●や×は具体的には求まりません。
というより、具体的に設定することはできますが、定まりません。
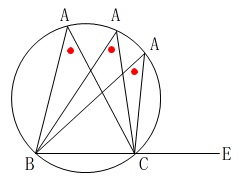頂点\(\,\mathrm{A}\,\)が1つの円周上を動いたとすると円周角となる\(\,\mathrm{∠BAC}\,\)は同じですが、
\(\,\mathrm{∠ABC}\,\)を2等分した角の大きさは変わるからです。

このことを考えれば定まらないというのは分かると思いますが、
ある特定の角でも成り立たなくてはならない（一般性がある）ので、
\(\,\mathrm{∠ABC}\,\)を適当に決めても\(\,x\,\)は求まります。

例えば、
　\(\,\mathrm{∠ABC=58^{\circ}}\,\)とすると、
　\(\,\mathrm{∠ACE=100^{\circ}}\,\)となり、
二等分された角はそれぞれ、
　\(\,\mathrm{∠DBC=29^{\circ}}\,\)
　\(\,\mathrm{∠DCE=50^{\circ}}\,\)
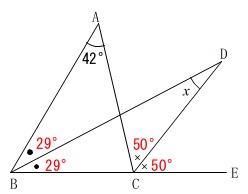このことから

　\(\begin{eqnarray}
x+29^{\circ}&=&50^{\circ}\\
x&=&\underline{　21^{\circ}　}
\end{eqnarray}\)

これを一般的に求めると、
　\(\,\mathrm{∠ABD=∠DBC}=\color{red}{a}\,\)
　\(\,\mathrm{∠ACD=∠DCE}=\color{blue}{b}\,\)

とすると、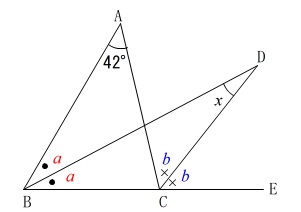　\(\begin{eqnarray}
x+\color{red}{a}&=&\color{blue}{b}\\
x&=&\color{blue}{b}-\color{red}{a}
\end{eqnarray}\)

となりますが、

　\(\begin{eqnarray}
42^{\circ}+2\color{red}{a}&=&2\color{blue}{b}\\
21^{\circ}+\color{red}{a}&=&\color{blue}{b}\\
21^{\circ}&=&\color{blue}{b}-\color{red}{a}
\end{eqnarray}\)

なので\(\,x=\underline{　21^{\circ}　}\,\)と求まります。

どちらも\(\,\color{magenta}{c}=\color{red}{a}+\color{blue}{b}\,\)となることを利用しています。

一般的な事実と、ある条件のときに成り立つ事実を使い分けることができれば良いですが、
何を言っているのかもわからないかもしれないので、笑
この問題のように角度が具体的に決まらない場合には文字を利用することに慣れておくと良いです。

この程度の問題に時間をかけている場合ではありませんので先を急ぎましょう。

(8)
連立方程式の解をグラフから求める不確実な方法をさせられます。

　　\( \begin{cases}
\hspace{7pt} y=x+6\\ \\
\hspace{7pt} x+2y=6
\end{cases}\)

の両方のグラフを書くと、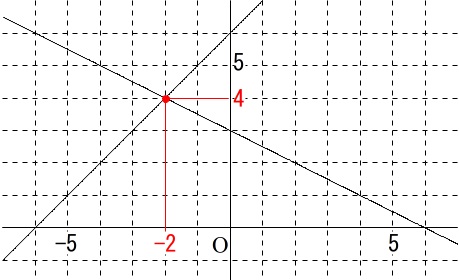
答え　\(\,\underline{　x=-2\,,\,y=4　}\,\)

2つの曲線の交点をグラフから読み取るのは不確実です。
この問題も交点を連立方程式の解として求めておくと良いですよ。

ちなみにですが、普通に扱う数学では曲線という言葉は直線を含んでいます。

⇒　直線は曲線の一部

（当会の高校数学サイトに移ります。）

\(\color{black}{\fbox{　1　}}\)はここまでです。

もう一度お伝えしておきます。
ここまでで\(\,43\,\)点配点されています。

垂線の作図とデータの活用（平均値と整数によるしぼり込み）

　\(\color{blue}{\fbox{　2　}}\)

作図とデータの活用です。

データの活用問題では平均値を扱いますが、整数の性質を含んでいて計算だけでは答えまで時間がかかるので手を動かしましょう。

(1)
垂線の作図ですので問題ないでしょう。

頂点\(\,\mathrm{A}\,\)から辺\(\,\mathrm{BC}\,\)に\(\,2\,\)点交わるように円を描き、
その\(\,2\,\)点から同じ半径の円を描いて交点を見つけ、
頂点\(\,\mathrm{A}\,\)と交点を結ぶだけです。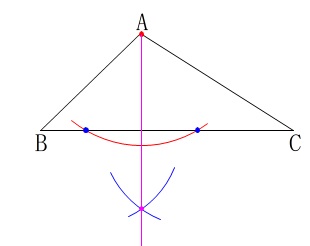

(2)
\(\,10\,\)人のデータがあります。
\(\,1\,\)人分の成功した回数と、平均値が分かっていません。

\(\,2\,\)人の会話から分かっていない成功回数と平均値を求めますが、
文字を使っても機械的には求まりません。

\(\,\mathrm{A}\,\)とか\(\,\mathrm{B}\,\)とか関係ないので、
分かっている\(\,9\,\)人のデータを成功した回数の多い人順に並べ直してみましょう。

　\(\,9,8,7,7,\color{red}{6},3,2,1,1\,\)

この中に\(\,\mathrm{G}\,\)の成功回数が加わります。

兄の話によると、
\(\color{black}{\fbox{　ア　}}\)に入る\(\,\mathrm{G}\,\)の人の成功した回数は真ん中より下の順位らしいので、
\(\,5\,\)位より下の順位で、平均値より成功回数は多い、ということが分かっています。

つまり、\(\color{black}{\fbox{　ア　}}\)には\(\,5\,\)位の\(\,\color{red}{6}\,\)より小さい値が入ります。
（順位の決め方から同順位はないので\(\,5\,\)位の\(\,6\,\)という数字は入りません。）

\(\,\mathrm{G}\,\)の成功回数が\(\,5\,\)回のとき、
全体の平均値は、
\(\,10\,\)人の成功回数を加えると\(\,49\,\)回となるので
　\(\hspace{10pt}\displaystyle \frac{49}{10} =4.9　(回)\)

これは\(\,\mathrm{G}\,\)の人の回数より少ない平均値なので適しています。

\(\,\mathrm{G}\,\)の成功回数が\(\,4\,\)回のとき、
全体の平均値は
\(\,10\,\)人の成功回数を加えると\(\,48\,\)回となるので
　\(\hspace{10pt}\displaystyle \frac{48}{10} =4.8　(回)\)

となるので平均値が\(\,\mathrm{G}\,\)の人の成功回数より多くなり不適です。

これ以下の成功回数はすべて兄の会話に適していません。

\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　5　}\,\)　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　4.9　}\,\)

不等式で解いても良いですが、
成功回数は整数なので調べ尽くしても大した時間はかかりませんよ。

ここまでで配点の半分以上があるので後半と分けます。

⇒　青森県公立高校入試2019年(平成31年)度の数学問題と解説【後半】

後半は図形と関数と規則性です。
規則性の読み取りには時間がかかると思われますので、前半をさっさと終わらせて時間を余らせておくと良いですね。

⇒　青森県公立高校入試2018数学の過去問と解説

\(\,2018\,\)年度の青森県立高校入試は\(\,1\,\)問ずつ、ていねいに解説してあります。笑
難易度と傾向はそれほど変わりませんので、見直しておくと良いですよ。

中学数学全体から偏りのない出題なので良い復習になります。