三重県公立高校入試2019年度前期数学の問題と解説【後半】

三重県で行われた公立高校入試2019年（平成31年）度の前期数学の問題と解説の後半です。
第4問は円柱と球の体積と整数の足し算問題、第5問は平面図形で平行四辺形の性質問題と回転体の体積を求める問題があります。
手を動かせば計算力はそれほど必要ではありませんので、問題の誘導にのって進めると良いですよ。

問題は三重県で公開してくれています。

⇒　2019年三重県公立高校入試【前期】数学の問題

前半では少し長くなってしまったので後半は簡単に済ませます。笑

円柱の体積と球の体積および整数の足し算

　\(\large{\color{black}{\fbox{　4　}}}\)

(1)体積の差を求める問題と、
(2)の自然数の足し算や引き算のいろいろな組み合わせと文字式の問題があります。

円柱の体積と球の体積の差

(1)
円柱は底面の直径と高さ\(\,\color{red}{6}\,\)が等しいので、
底面の直径が\(\,\color{red}{6}\,\)なので　底面の半径は\(\,\color{blue}{3}\,\)です。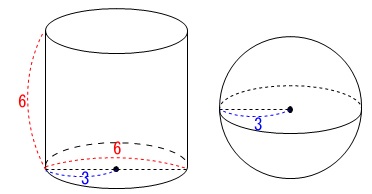
円柱の体積\(\,\mathrm{V_1}\,\)は、
　\(\begin{eqnarray}
\mathrm{V_1}&=&\pi\,\times (3)^2\times 6\\
&=&\color{red}{54\,\pi}
\end{eqnarray}\)

球の半径は\(\,\color{blue}{3}\,\)なので球の体積\(\,\mathrm{V_2}\,\)は、
　\(\begin{eqnarray}\displaystyle
\mathrm{V_2}&=&\frac{4}{3}\times \pi\,\times (3)^3\\
&=&\color{blue}{36\,\pi}
\end{eqnarray}\)

よって求める体積の差は
　\(\begin{eqnarray}
\mathrm{V_1-V_2}&=&\color{red}{54\,\pi}-\color{blue}{36\,\pi}\\
&=&\underline{　18\,\pi　}　(\mathrm{cm^3})
\end{eqnarray}\)

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

球の体積や表面積を求める公式は中学生には証明できないので覚えていないと使えません。

自然数の足し算引き算の組合わせ

(2)
自然数の足し算引き算は整数の足し算です。
正の数だけが足されたとき最大で、負の数を加えると小さくなる、ということが分かっていれば問題ありません。

自然数\(\,a\,\)の数が\(\,\color{red}{n}\,\)個のとき、
\(\,+\,\)と\(\,-\,\)は\(\,(\color{blue}{n-1})\,\)個になります。

①
\(\,a=2\,,\,n=4\,\)の場合、
\(\,2\,\)が\(\,\color{red}{4}\,\)個で\(\,+\,\)と\(\,-は\,\)合わせて\(\,\color{blue}{3}個\,\)あります。

　\(\,2+2+2+2=8\,\)
　\(\,2+2+2-2=4\,\)
　\(\,2+2-2-2=0\,\)
　\(\,2-2-2-2=-4\,\)
の\(\,4\,\)通りの計算結果が出ます。

答え　\(\,\underline{　8\,,\,4\,,\,0\,,\,-4　}\,\)

計算の最初の\(\,2\,\)には省略された\(\,+\,\)だけというのがポイントです。

②
\(\,\color{red}{a}\,\)が\(\,\color{blue}{n}\,\)個あるので、
計算結果はすべて足し算のとき最大で
　\(\hspace{10pt}\color{red}{a}\times \color{blue}{n}=\color{red}{an}\)

最初の\(\,a\,\)以外の\(\,(n-1)\,\)個すべてが引き算になるとき計算結果が最小で、
　\(\hspace{10pt}a-a\times (n-1)=\color{blue}{2a-an}\)

よってこれらの差は、
　\(\hspace{10pt}\color{red}{an}-\color{blue}{2a-an}\\
=\underline{　2an-2a　}\)

最大になるときと最小になるときは図Ⅰの結果を見てもおおよそ検討がつきます。

③
②の続きになります。

　\(2an-2a=50\)

となる自然数\(\,a\,\)をすべて求めるということです。

　\(\begin{eqnarray}
2an-2a&=&50\\
2a(n-1)&=&50\\
a(n-1)&=&25
\end{eqnarray}\)

と変形できて、\(\,a\,\)が自然数なので\(\,(n-1)\,\)も自然数になります。
でなければかけて\(\,+25\,\)にはなりませんからね。

かけて\(\,25\,\)になる自然数の組は、
　\(\,1\times 25\,,\,5\times 5\,,\,25\times 1\,\)
だけなので、
　\(a=1\,,\,n-1\,=\,25\)
　\(a=5\,,\,n-1\,=\,5\)
　\(a=25\,,\,n-1\,=\,1\)
の\(\,3\,\)組になります。

答え　\(\,\underline{　a=1\,,\,5\,,\,25　}\,\)

必要無いので\(\,n\,\)の値を求めていませんが、
　\(n=26\,,\,6\,,\,2\)
と個数である自然数になっています。

\(\large{\color{black}{\fbox{　4　}}}\)はこれだけです。
　

平行四辺形の性質と中点連結定理

平行四辺形と中点が2つ与えられています。
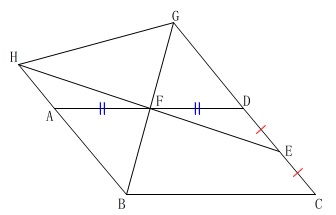合同な三角形がいくつもあるので証明もしやすく、長さの比も出しやすいです。

三角形の合同の証明

(1)
\(\,\mathrm{△BFH}\,\)と\(\,\mathrm{△GFE}\,\)が合同であることの証明です。
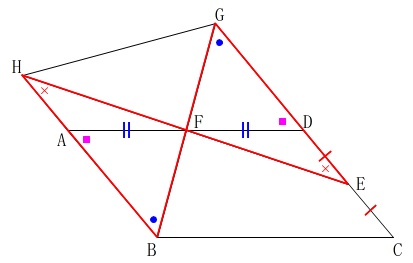平行線の錯角が等しいことと、
\(\,\mathrm{F}\,\)が\(\,\mathrm{AD}\,\)の中点であること、
また対頂角が等しいことから
　\(\,\mathrm{△AFH}\,\)　≡　\(\,\mathrm{△DFE}\,\)
および
　\(\,\mathrm{△AFB}\,\)　≡　\(\,\mathrm{△GFD}\,\)
の証明は簡単にできます。
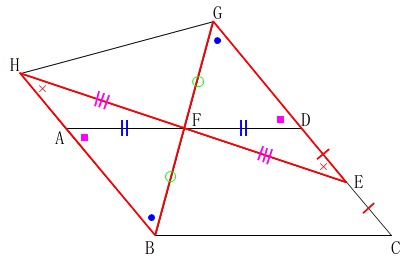このことから等しい辺や角が分かるので、
　\(\,\mathrm{△BFH}\,\)≡\(\,\mathrm{△GFE}\,\)
合同条件は、
　\(\,1\,\)組の辺とその両端の角がそれぞれ等しい。
または
　\(\,2\,\)組の辺とその間の角がそれぞれ等しい。
のどちらでも良いですよ。

証明は省略します。笑

⇒　中学２年 平行と合同と証明の書き方ポイントまとめ

証明の書き方は好きにしていいですけど、合同条件を忘れずに書くようにしましょう。

線分比と三角形の面積

(2)
ここから長さと面積が出てきます。

　\(\,\mathrm{BC=4}\,\)
　平行四辺形\(\,\mathrm{ABCD}\,\)の面積は\(\,\color{magenta}{6}\,\)

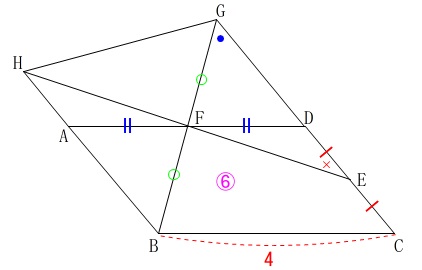
①
\(\,\mathrm{△DGF}\,\)の面積は、\(\,\mathrm{△BAF}\,\)の面積に等しくて、
\(\,\mathrm{F}\,\)が\(\,\mathrm{AD}\,\)の中点なので、
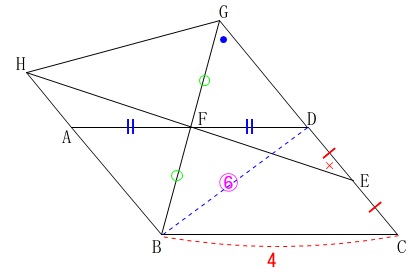平行四辺形\(\,\mathrm{ABCD}\,\)の半分である\(\,\mathrm{△ABD}\,\)のさらに半分だから、
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGF}&=&\mathrm{△BAF}\\
&=&\color{magenta}{6}\times \frac{1}{2}\times \frac{1}{2}\\
&=&\underline{　\frac{3}{2}　}　(\mathrm{cm^2})
\end{eqnarray}\)

面積比と線分比

②
辺\(\,\mathrm{BF}\,\)上に\(\,\mathrm{△DEF}\,\)と\(\,\mathrm{△BCI}\,\)の面積が等しくなるように\(\,\mathrm{I}\,\)をとります。
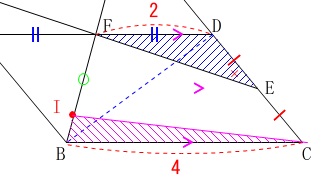\(\,\mathrm{△DEF}\,\)の底辺と見なせる\(\,\mathrm{FD}\,\)は\(\,\mathrm{BC}\,\)の半分の長さなので、
高さは\(\,\mathrm{△BCI}\,\)の\(\,2\,\)倍になります。

\(\,\mathrm{DC}\,\)の中点\(\,\mathrm{E}\,\)から\(\,\mathrm{FD,BC}\,\)に平行となる直線を引き、
\(\,\mathrm{BG}\,\)との交点を\(\,\mathrm{J}\,\)とすると、
　\(\mathrm{BI:IJ:JF}=1:1:2\)
となるので

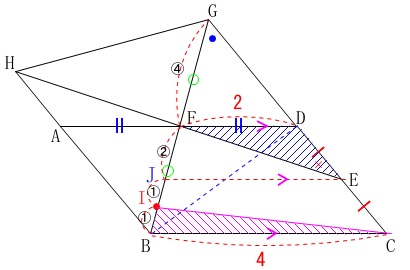
　\(\mathrm{BI:IG}=\underline{　1:7　}\)

垂直な線分として高さは出していませんが、相似を利用すれば高さの比に垂線は必要ありません。

⇒　神奈川県公立高校入試2018の数学問4関数と図形融合問題の解説

他にも詳しく解説している問題もあるので見ておくと良いです。

三角形を回転させた体積

③
\(\,\mathrm{△BCI}\,\)を\(\,\mathrm{BC}\,\)を軸として回転させた立体の体積を求めます。
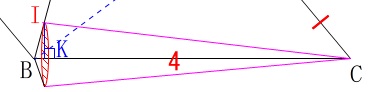回転体は円すい2つを合わせた形になりますが、底面積は等しいので別々に計算する必要はありません。

底面となる円の半径を求めておきましょう。
\(\,\mathrm{I}\,\)から\(\,\mathrm{BC}\,\)に下ろした垂線の足を\(\,\mathrm{M}\,\)とします。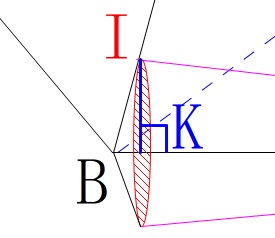
\(\,\mathrm{△BCI}\,\)の面積は\(\,\mathrm{△DEF}\,\)と等しく、
平行四辺形の面積\(\,\color{magenta}{6}\,\)の\(\displaystyle \,\frac{1}{8}\,\)倍なので
　\(\begin{eqnarray}
\mathrm{△BCI}&=&\mathrm{△DEF}\\
&=&\color{magenta}{6}\times \frac{1}{8}\\
&=&\color{red}{\frac{3}{4}}
\end{eqnarray}\)
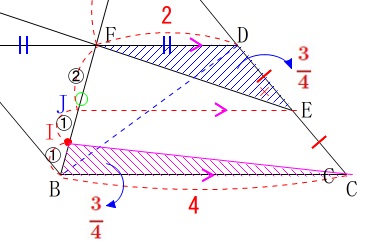\(\,\mathrm{△BCI}\,\)の底辺\(\,\mathrm{BC}\,\)の長さは\(\,\color{red}{4}\,\)なので、

　\(\begin{eqnarray}
\mathrm{△BCI}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{IK}\\
\color{red}{\frac{3}{4}}&=&\frac{1}{2}\times \color{red}{4}\times \mathrm{IK}\\
\mathrm{IK}&=&\color{blue}{\frac{3}{8}}
\end{eqnarray}\)

よって求める回転体の体積\(\,\mathrm{V}\,\)は、
底面の半径が\(\displaystyle \,\frac{3}{8}\,\)で高さが\(\,4\,\)の円すいと同じなので、

　\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{1}{3}\times \pi\,\left(\color{blue}{\frac{3}{8}}\right)^2\times \color{red}{4}\\
&=&\underline{　\frac{3}{16}\,\pi　}　(\mathrm{cm^3})
\end{eqnarray}\)

以上が\(\,2019\,\)年度の三重県公立高校前期選抜数学問題です。

⇒　2019年(平成31年)度三重県【前期】公立高校入試数学の問題と解説

前半の小問集合から見直しておきましょう。

⇒　三重県公立高校入試の数学の問題と解説

\(\,2018\,,\,2020\)年も同様なので時間配分などの目安にすると良いですね。