2019年(平成31年)度三重県【前期】公立高校入試数学の問題と解説

2019年(平成31年)度に三重県で行われた公立高校入試【前期】数学の問題と解説です。
広い範囲を偏りなく出題されていますので苦手分野を作らないように中学数学全般の基本を中心とした対策が効果的です。
ただ、この年の問題の中で1つだけ解答が他にも存在する、条件があいまいな問題がありますので確認しておきましょう。

※群馬県と間違えて三重県の前期問題を説明していました。
このページは三重県の過去問解説です。<(_ _)>

問題は三重県で公開してくれています。

⇒　2019年三重県公立高校入試【前期】数学の問題

長々と説明する必要もない基本的な問題が並びますので簡単に済ませます。
わかりにくい所は他県の問題でも同じような問題がたくさんありますので参考にすると良いですよ。

それでもわからないところはお問い合わせフォームからでも結構ですので質問して下さい。

式の計算、方程式、平均値、作図などの小問集合

　\(\large{\color{black}{\fbox{　1　}}}\)

悩むことがない程突っ走れば良い簡単な計算が多い小問集合です。

式の計算と代入

(1)
計算順序と符号に気をつければ問題ありません。

　\(\hspace{10pt}-18\div 3^2\\
=-18\div 9\\
=\underline{　-2　}\)

(2)
展開した式は書いて計算を進めた方がミスは減ります。

　\(\hspace{10pt}4(x-1)+3(x-2)\\
=4x-4+3x-6\\
=\underline{　7x-10　}\)

(3)
文字の値を代入するのは与式（求値式）を計算してからです。

　\(\hspace{10pt}6xy\color{red}{\div (-2x)^2}\times (-12x^2y)\\
=6xy\color{red}{\div 4x^2}\times (-12x^2y)\\
\displaystyle =-\frac{6xy\times 12x^2y}{\color{red}{4x^2}}\\
=-18xy^2\\
\displaystyle =-18\times (-2)\times \left(\frac{1}{3}\right)^2\\
\displaystyle =\frac{18\times 2}{9}\\
=\underline{　4　}\)

割り算は逆数のかけ算として処理しますが、\(\,\div\,\)の直後を分母にまわして分数計算（約分）をするだけです。

(4)
直線に限らず交点は連立すれば求まります。
その交点を1つの直線が通るので代入すれば良いだけです。

　\( \begin{cases}
\hspace{7pt} x+y=5　･･･①\\ \\
\hspace{7pt} x+2y=4　･･･②
\end{cases}\)

交点はこの連立方程式を加減法で解いて簡単に求まります。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

　\(\hspace{25pt}x+y=5\\
\underline{-)\hspace{10pt}x+2y=4}\\
\hspace{30pt}-y=1\\
\hspace{40pt}y=-1\)

これを①か②に代入して\(\,x\,\)を求めると、
　\(\begin{eqnarray}
x+(-1)&=&5\\
x&=&6
\end{eqnarray}\)

交点は\(\,(\,6\,,\,-1\,)\,\)で、
交点が直線\(\,y=ax+1\,\)を通ることから代入します。

　\(\begin{eqnarray}\displaystyle
-1&=&a\times (6)+1\\
-1&=&6a+1\\
-6a&=&2\\
a&=&\underline{　-\frac{1}{3}　}
\end{eqnarray}\)

無理数の計算と方程式の解

(5)
無理数の展開計算と分母の有理化です。

　\(\hspace{10pt}\displaystyle (\sqrt{5}+2)(\sqrt{5}-7)-\color{red}{\frac{5}{\sqrt{5}}}\\
\displaystyle =(5-5\sqrt{5}-14)-\color{red}{\frac{5\sqrt{5}}{5}}\\
=-9-5\sqrt{5}-\sqrt{5}\\
=\underline{　-9-6\sqrt{5}　}
\)

(6)
方程式を解くときの基本は展開してすべての項を左辺に集めることからです。

　\(\begin{eqnarray}
\color{red}{(x-5)(x+2)}&=&\color{blue}{-10}\\
\color{red}{x^2-3x-10}\color{blue}{+10}&=&0\\
x^2-3x&=&0\\
x(x-3)&=&0\\
x&=&\underline{　0\,,\,3　}
\end{eqnarray}\)

解の1つ\(\,x=0\,\)を忘れように注意しておきましょう。

⇒　2次方程式の因数分解を利用する解き方のコツと注意点

正の数負の数の大小と平均値および作図

(7)
一般的になり立つ場合、具体的な数値（取り上げた1つの例）でも成り立たなくてはなりません。

　\(a=2\,,\,b=-3\)

とすると

　\(-a=-2\,,\,-b=+3\,,\,a-b=5\,,\,b-a=-5\)

よって、小さい順に並べると
　
　\(\underline{　b-a\,,\,b\,,\,-a\,,\,a\,,\,-b\,,\,a-b　}\)

これは一般的に成り立ちます。

(8)
\(\,\mathrm{A,B}\,\)の二組合わせて\(\,70\,\)人です。

　\(\,\mathrm{A}\,\)組の人数を\(\,\color{red}{x}\,\)
とすると
　\(\,\mathrm{B}\,\)組の人数は\(\,\color{blue}{70-x}\,\)
となるので、全体の平均値は
　\(\hspace{10pt}\displaystyle \frac{81\times \color{red}{x}+88\times (\color{blue}{70-x})}{70}\)

これが\(\,84.4\,\)となるので
　\(\begin{eqnarray}\displaystyle
\frac{81\,x+88\,(\,70-x\,)}{70}&=&84.4\\
81\,x+88\,(\,70-x\,)&=&84.4\times 70\\
81x+6160-88x&=&5908\\
-7x&=&-252\\
x&=&\underline{　36　(人)}
\end{eqnarray}\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値は必ずといって良いほど出題されますよ。

(9)
\(\,135°\,\)の作図です。

　\(135=90+45\)
なので、
　\(\,180°\,\)の角の二等分線
と
　\(\,90°\,\)の角の二等分線
を作図すれば良いだけです。

直線\(\,\mathrm{AO}\,\)に\(\,\mathrm{O}\,\)を通る垂線を引いて
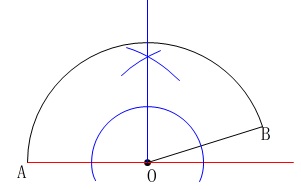\(\,\mathrm{B}\,\)側にもう一度角の二等分線を引けば終わりです。

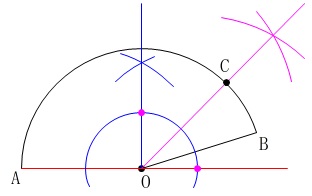
最初に\(\,\mathrm{O}\,\)を中心とする円を書きましたが、半径\(\,\mathrm{OA}\,\)の円を利用しても同じです。

度数分布表と確率

　\(\color{black}{\fbox{　2　}}\)

データと確率の\(\,2\,\)問あります。

相対度数と代表値（答えに注意）

(1)
度数分布表に関する問題です。

①
相対度数はその階級の度数を度数合計で割れば求まります。

\(\,26\,\mathrm{m}\,\)以上\(\,30\,\mathrm{m}\,\)未満の階級の度数は\(\,4\,\)なので

　\(\hspace{10pt}\displaystyle \frac{4}{25}=\underline{　0.16　}\)

②
中央値が\(\,18\,\mathrm{m}\,\)以上\(\,22\,\mathrm{m}\,\)未満の階級にあるということは、
　全体\(\,25\,\)人中の小さい方から\(\,13\,\)人目はこの階級にいる
ということです。
これは\(\color{black}{\fbox{　(ア)　}}\)が\(\,5\,\)人以上だということになります。

最頻値が\(\,24\,\mathrm{m}\,\)ということは、
　\(\,22\,\mathrm{m}\,\)以上\(\,36\,\mathrm{m}\,\)未満の階級の度数は\(\,6\,\)人以上
ということです。
\(\,6\,\)人以上でなければ最頻値が変わってきます。

全体で\(\,25\,\)人だから他の階級の度数から、
\(\color{black}{\fbox{　(ア)　}}\)と\(\color{black}{\fbox{　(イ)　}}\)は合わせると\(\,12\,\)人なので、

　\(\color{black}{\fbox{　(ア)　}}\)\(\,\underline{　5　}\,\) , \(\color{black}{\fbox{　(イ)　}}\)\(\,\underline{　7　}\,\)

この組合わせ以外は中央値と最頻値が一致しません。

\(\color{red}{\fbox{\(\,\color{red}{　注意　}\,\)}}\)
度数分布表での最頻値は度数が一番多い階級の階級値になります。
\(\color{black}{\fbox{　(ア)　}}\)と\(\color{black}{\fbox{　(イ)　}}\)が\(\,6\,\)人で同じとき、
最頻値は\(\,\mathrm{16\,m}\,\)と\(\,\mathrm{24\,m}\,\)の2つになります。

この場合、確かに\(\,\mathrm{24\,m}\,\)も最頻値ではありますが、
ここでは問題の条件は\(\,\mathrm{24\,m}\,\)だけが最頻値になると見て良いでしょう。
採点はどうしたんでしょうね。
私が何か条件を見落としたかな？笑
気づいた方はご一報下さい。

正六角形の頂点で正三角形と二等辺三角形になる確率

(2)
正六角形の頂点3つを選んで三角形を作るというだけです。

①
3つのカードの取り出し方は、
　\(\begin{array}{|c|c|c|c|} \hline
\,A\, &\, B \,& \,C \,& \\ \hline
A & B & D & \\ \hline
A & B & E & \\ \hline
A & B & F & \\ \hline
A & C & D & \\ \hline
A & C & E & \,\color{red}{●}\,\\ \hline
A & C & F & \\ \hline
A & D & E & \\ \hline
A & D & F & \\ \hline
A & E & F & \\ \hline
B & C & D & \\ \hline
B & C & E & \\ \hline
B & C & F & \\ \hline
B & D & E & \\ \hline
B & D & F & \color{red}{●}\\ \hline
B & E & F & \\ \hline
C & D & E & \\ \hline
C & D & F & \\ \hline
C & E & F & \\ \hline
D & E & F & \\ \hline
\end{array}\)
の全部で\(\,20\,\)通りあって、
正三角形になるのは\(\,\color{red}{●}\,\)の付いた\(\,2\,\)通りなので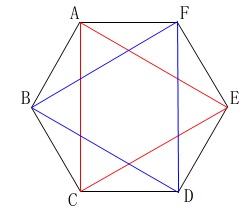
　\(\hspace{10pt}\displaystyle \frac{2}{20}=\underline{　\frac{1}{10}　}\)

②
今度は二等辺三角形になる確率です。
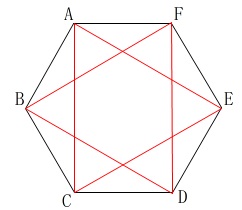
正三角形は二等辺三角形でもあるので忘れずに数えなければなりませんが、
問題が「ただし、正三角形になる場合も含む」と教えてくれています。

　\(\begin{array}{|c|c|c|c|} \hline
\,A\, &\, B \,& \,C \,& \,\color{blue}{○}\,\\ \hline
A & B & D & \\ \hline
A & B & E & \\ \hline
A & B & F & \,\color{blue}{○}\,\\ \hline
A & C & D & \\ \hline
A & C & E & \,\color{red}{●}\,\\ \hline
A & C & F & \\ \hline
A & D & E & \\ \hline
A & D & F & \\ \hline
A & E & F & \,\color{blue}{○}\,\\ \hline
B & C & D & \,\color{blue}{○}\,\\ \hline
B & C & E & \\ \hline
B & C & F & \\ \hline
B & D & E & \\ \hline
B & D & F & \color{red}{●}\\ \hline
B & E & F & \\ \hline
C & D & E & \,\color{blue}{○}\,\\ \hline
C & D & F & \\ \hline
C & E & F & \\ \hline
D & E & F & \,\color{blue}{○}\,\\ \hline
\end{array}\)

正三角形も含め\(\,8\,\)通りの二等辺三角形があるので、
　\(\hspace{10pt}\displaystyle \frac{8}{20}=\underline{　\frac{2}{5}}　\)

袋から取り出すことと正六角形の頂点とを合わせる問題ですが、袋のカードは必要無い問題ですよ。
問題をよく読んでシンプルに考えていきましょう。

長方形の辺上を動く2点と三角形の面積

　\(\large{\color{black}{\fbox{　3　}}}\)

長方形の辺上を動く2点と三角形の面積の変化を見ます。

具体的な面積から関数やグラフなどが問われますが、動点問題の考え方はどれも同じです。

問題の条件を簡単にまとめると、
　長方形\(\,\mathrm{ABCD}\,\)の辺上を\(\,\mathrm{P,Q}\,\)の\(\,2\,\)点が同じ速さ秒速\(\,\mathrm{1\,cm}\,\)で動く。
　点\(\,\mathrm{P}\,\)は\(\,\mathrm{A→B→A}\,\)の順に移動する。
　点\(\,\mathrm{Q}\,\)はの順に移動する。

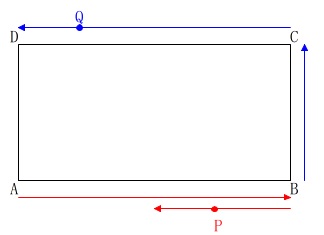
ただし、点\(\,\mathrm{Q}\,\)が\(\,\mathrm{D}\,\)に到着したら点\(\,\mathrm{P}\,\)は移動を停止するので、
\(\,\mathrm{B→C→D}\,\)の移動時間\(\,4+8=12\,\)秒後には点\(\,\mathrm{P}\,\)は移動を停止します。
　このとき点\(\,\mathrm{P}\,\)は\(\,\mathrm{B}\,\)で折り返した後、辺\(\,\mathrm{AB}\,\)の中点で止まります。
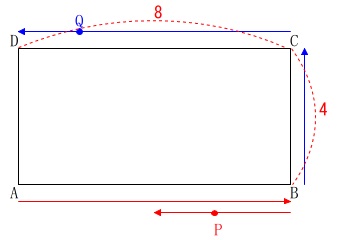これくらいのことが分かれば後は、点が動く問題での基本的な取り組みをすれば楽に進みます。

点が動く問題では変化の起こるところで場合をわけて考えます。

点\(\,\mathrm{P}\,\)は\(\,8\,\)秒後に\(\,\mathrm{B}\,\)に到達して折り返すので、
変化が起こるのは\(\,\color{red}{8}\,\)秒後です。

点\(\,\mathrm{Q}\,\)は\(\,4\,\)秒後に\(\,\mathrm{C}\,\)に到達して\(\,\mathrm{D}\,\)に向くので、
変化が起こるのは\(\,\color{blue}{4}\,\)秒後です。

このことから
　\(\,0≦x≦\color{blue}{4}\,\)
　\(\,\color{blue}{4}≦x≦\color{red}{8}\,\)
　\(\,8≦x≦12\,\)
で別々に考えれば良いのです。

この問題では一気に解決する必要はありませんので、問題の順番通りに解いて行きます。

具体的な面積の求め方

(1)
点\(\,\mathrm{P,Q}\,\)が出発して3秒後、
　点\(\,\mathrm{P}\,\)は辺\(\,\mathrm{AB}\,\)上
　点\(\,\mathrm{Q}\,\)は辺\(\,\mathrm{BC}\,\)上
にいます。
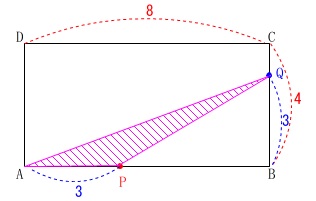このとき\(\,\mathrm{△APQ}\,\)は底辺\(\,\color{blue}{3}\,\)、高さ\(\,\color{blue}{3}\,\)なので、
　\(\begin{eqnarray}
y&=&\frac{1}{2}\times 3\times 3\\
&=&\underline{　\frac{9}{2}　}
\end{eqnarray}\)

(2)
　\(4≦x≦8\)
\(\,4\,\)秒後から\(\,8\,\)秒後の\(\,\mathrm{△APQ}\,\)の面積\(\,y\,\)の関数を求めます。

\(4≦x≦8\)のとき、
　点\(\,\mathrm{P}\,\)は\(\,\mathrm{ＡＢ}\,\)上
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{ＣＤ}\,\)上
にいます。

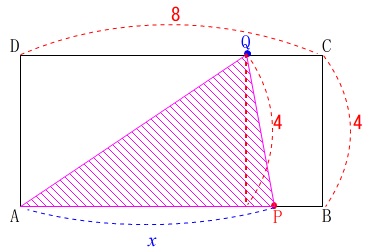
このとき\(\,\mathrm{△APQ}\,\)の底辺は\(\,\mathrm{AP}\,\)の\(\,\color{blue}{x}\,\)で、高さは\(\,\color{red}{4}\,\)で一定なので、
　\(\begin{eqnarray}
y&=&\frac{1}{2}\times \color{blue}{x}\times \color{red}{4}\\
&=&\underline{　2x　}　(\,4≦\,x\,≦\,8\,)
\end{eqnarray}\)

(3)
答えは(2)を満たすグラフは1つしかないのですぐに分かります。

答え　\(\,\underline{　イ　}\,\)

確かめたければ全部の区間で関数を表しておきます。

①\(0≦x≦4\)のとき
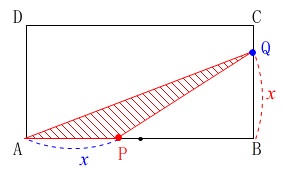底辺は\(\,\color{blue}{x}\,\)、高さは\(\,\color{red}{x}\,\)なので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times x\\
&=&\frac{1}{2}\,x^2
\end{eqnarray}\)

②\(4≦x≦8\)のときは(2)で求めていますがもう一度見ておくと、
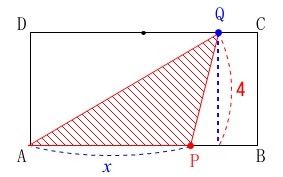底辺が\(\,\color{blue}{x}\,\)、高さが\(\,\color{red}{4}\,\)なので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \color{blue}{x}\times \color{red}{4}\\
&=&2x
\end{eqnarray}\)

③\(8≦x≦12\)のとき、
点\(\,\mathrm{P}\,\)について、
　\(\,\mathrm{A→B→A}\,\)と動いたとすると\(\,8+8=\color{red}{16}\,\)
なので、\(\,\mathrm{B}\,\)を折り返した後\(\,\mathrm{AP}=\color{blue}{16-x}\,\)となります。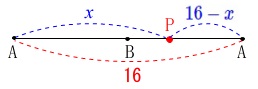
このとき\(\,\mathrm{△APQ}\,\)の面積\(\,y\,\)は、

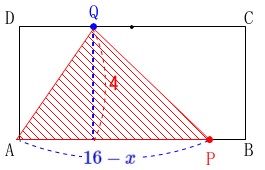
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \color{blue}{16-x}\times \color{red}{4}\\
&=&32-2x
\end{eqnarray}\)

①②③をつなぐと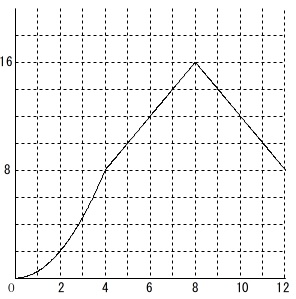　\(\,\underline{　イ　}\,\)のグラフになります。

(4)
\(\,\mathrm{△APQ}\,\)の面積が長方形\(\,\mathrm{ABCD}\,\)の\(\displaystyle \frac{1}{6}\)倍になるということは、
長方形\(\,\mathrm{ABCD}\,\)の面積が\(\,8\times 4=\color{red}{32}\,\)なので、
\(\,\mathrm{△APQ}\,\)の面積が
　\(\hspace{10pt}\displaystyle \color{red}{32}\times \frac{1}{6}=\frac{16}{3}\)
になるときです。

(3)のグラフを見てわかるように、
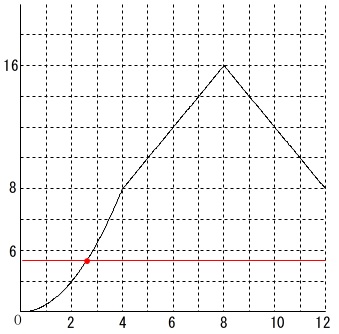\(\,0\,≦\,x\,≦\,4\,\)のときしかありません。

\(\,0\,≦\,x\,≦\,4\,\)のとき\(\displaystyle \,y=\frac{1}{2}\,x^2\,\)なので

　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\,x^2&=&\frac{16}{3}\\
x^2&=&\frac{32}{3}\end{eqnarray}\)
\(\,x＞\,\)0なので
　\(\begin{eqnarray}\displaystyle
x&=&\frac{\sqrt{32}}{\sqrt{3}}\\
&=&\frac{4\sqrt{2}}{\sqrt{3}}\\
&=&\underline{　\frac{4\sqrt{6}}{3}　}
\end{eqnarray}\)

(5)
\(\,\mathrm{△APQ}\,\)が直角三角形になるのは、
　①\(\,\mathrm{∠APQ=90°}\,\)
　②\(\,\mathrm{∠AQP=90°}\,\)
　③\(\,\mathrm{∠QAP=90°}\,\)
の\(\,3\,\)通りが考えられます。
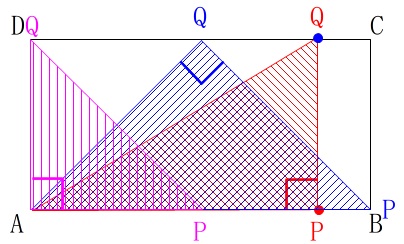すぐに点の位置が分かるわけではありませんので、確かめていきます。

点\(\,\mathrm{Q}\,\)は\(\,\mathrm{B→C→D}\,\)と\(\,\mathrm{D}\,\)まで動いたときに\(\,12\,\)秒なので、
\(\,\mathrm{B→C→Q}\,\)と動いた\(\,x\,\)秒後は、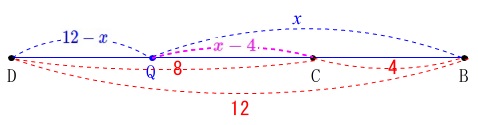
　\(\,\mathrm{CQ}=\color{magenta}{x-4}\,\)
　\(\,\mathrm{DQ}\,=\color{blue}{12-x}\,\)
となります。

①\(\,\mathrm{∠APQ=90°}\,\)になるのは、
\(\,\mathrm{AP}\,\)と\(\,\mathrm{PQ}\,\)が垂直になるときで、
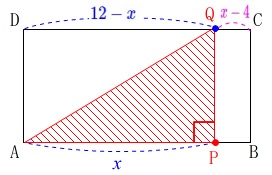\(\,\mathrm{AP=DQ}\,\)のときだから
　\(\begin{eqnarray}
x&=&12-x\\
2x&=&12\\
x&=&\underline{　6　}　秒後
\end{eqnarray}\)

②\(\,\mathrm{∠AQP=90°}\,\)になるのは、
\(\,\mathrm{AP}\,\)と\(\,\mathrm{PQ}\,\)が垂直になるときで、
点\(\,\mathrm{Q}\,\)が\(\,\mathrm{DC}\,\)の中点になるとき
　\(\mathrm{AQ=BQ}=\color{red}{4\sqrt{2}}\)
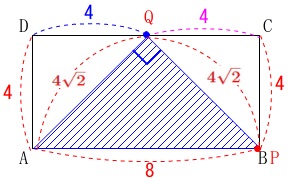直感的ですが、\(\,\mathrm{△AQP}\,\)は直角三角形になるので答えに加えます。

このとき点\(\,\mathrm{P,Q}\,\)が出発してから\(\,8\,\)秒後で
　\(\,x=\underline{　8　}\,\)

三平方の定理できっちり求めようかと思いましたがやめました。笑
やってみるなら\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)を折り返す前と後で分けて考えて見ると良いです。

③\(\,\mathrm{∠QAP=90°}\,\)になるのは、
\(\,\mathrm{AP}\,\)と\(\,\mathrm{QA}\,\)が垂直になるときで
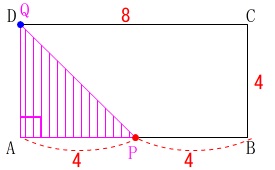点\(\,\mathrm{Q}\,\)が\(\,\mathrm{D}\,\)に到着したときで、点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)を折り返し\(\,\mathrm{AB}\,\)の中点まで来たときです。