トレミーの定理の証明方法は1つではありません。
ここでは中学生でもできる方法を示しておきます。
ただし、中学生の普通の作業ではなかなか気がつくことではないので、証明よりは使う機会があれば使えることを優先していいでしょう。
高校生の証明の仕方は他にありますので別に示します。
トレミーの定理
先ずは定理を確認しておきましょう。
【トレミーの定理】
円に内接する四角形\(\,ABCD\,\)において、
対辺の長さの和は対角線の長さの積に等しい。
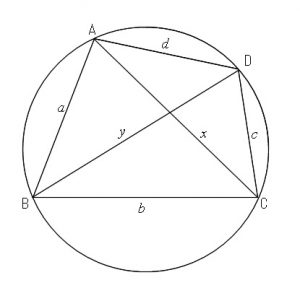
すなわち、
\(AB=a\,,\,BC=b\,,\,CD=c\,,\,DA=d\)
とし、\(AC=x\,,\,BD=y\) とすると
\(\color{red}{\large{ac+bd=xy}}\)
である。
中学生ができる証明方針
高校生が三角比を使って証明するのは普通です。
しかし、次のように相似を利用して中学生でも証明することができるのです。
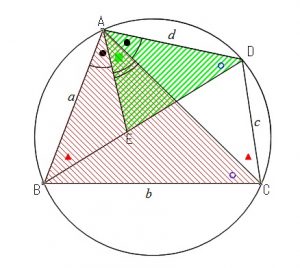
下の図のように
\(\angle BAE=\angle CAD\)
となる点\(\,E\,\)を取り、 \(\color{red}{・・・☆}\)
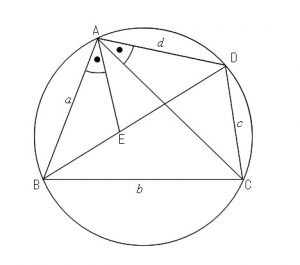
円周角が等しいことを利用すると、
\(\triangle ABE\) ∽ \(\triangle ACD\) ・・・①
\(\triangle AED\) ∽ \(\triangle ABC\) ・・・②
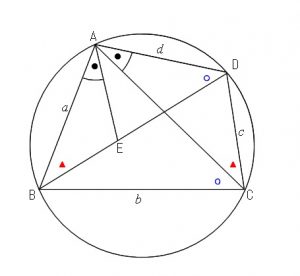
この2つの相似から辺の比を利用して簡単に証明できます。
①より
\(\displaystyle \frac{AB}{BE}=\frac{AC}{CD}\)
②より
\(\displaystyle \frac{AD}{ED}=\frac{AC}{BC}\)
これらの分母を払って加えると終了です。
中学数学の範囲での補助線は平行線か、垂線がほとんどなので、
\(\color{red}{☆}\) の利用はちょっと技巧的といってもいいでしょう。
なかなか気がつくものではありませんね。
詳しく証明をしておきます。
トレミーの定理の証明
\(\,BD\,\)上に
\(\angle BAE=\angle CAD ・・・①\)
となるように点Eを取る。
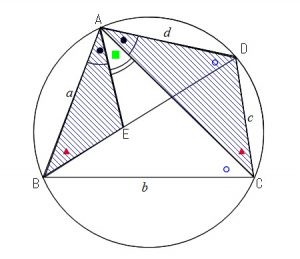
\(\triangle ABE\) と \(\triangle ACD\) において
弧ADに対する円周角であることから
\(\angle ABE=\angle ACD ・・・②\)
①②より
\(\triangle ABE\) ∽ \(\triangle ACD\)
このことから
\(\hspace{16pt}\color{red}{AB}\,:\,\color{blue}{BE}\,=\,\color{blue}{AC}\,:\,\color{red}{CD}\, \\ \\
\Leftrightarrow\,\color{red}{AB} \cdot \color{red}{CD}\,=\,\color{blue}{AC} \cdot \color{blue}{BE} ・・・③\)
次に \(\triangle AED\) と \(\triangle ABC\) において
\(\angle EAC\) を共通の角とみると
\(\angle EAD=\angle CAD\,+\,\color{red}{\angle EAC}\)
\(\angle BAC=\angle BAE\,+\,\color{red}{\angle EAC}\)
\(\angle CAD=\angle BAE\) なので
\(\angle EAD=\angle BAC ・・・④\)
また、
弧ABの円周角であることから
\(\angle ADE=\angle ACB ・・・⑤\)
④⑤より
\(\triangle AED\) ∽ \(\triangle ABC\)
このことから
\(\hspace{16pt}\color{red}{AD}:\color{blue}{DE}=\color{blue}{AC}:\color{red}{CB}\\ \\
\Leftrightarrow \,\color{red}{AD}\cdot \color{red}{CB}=\color{blue}{AC}\cdot \color{blue}{DE} ・・・⑥\)
③と⑥の両辺を加えることにより
\(AB \cdot CD+BC\cdot AD=AC \cdot BE+AC\cdot DE\)
右辺は
\(AC \cdot BE+AC\cdot DE\\ \\
=AC(\color{red}{BE+ED})=AC\cdot \color{red}{BD}\)
\( ∴ AB \cdot CD+BC\cdot AD=AC\cdot BD\\ \\
\hspace{20pt} \Leftrightarrow \hspace{5pt}\color{red}{ac+bd=xy}\)
証明の際、三角形の相似条件を書いていませんが、
高校生なら相似の証明は「二角相等」を言わずに進めて良いでしょう。
(中学生に誘導条件なしで「証明せよ」という問題は出ない、としておきます。)
三角比で定理を学んだ後なら、
余弦定理を使って証明できます。
三角比を利用した証明の方が計算だけで済むので導くには楽かもしれません。