代金や速さの連立方程式の文章問題の解き方と線分図の利用方法です。
連立方程式は方程式を連立するということなので、文章から２つの条件を抜き出すことが重要になります。
問題文の中から方程式を立てられるだけの条件を見つけ出す練習をやっておきましょう。
代金の問題と道のり、速さ、時間の練習問題ですが線分図をかくという１つの作業で差が出ます。
代金の問題の解き方
代金に関する基本問題を１つ残していました。
日本語の文章題から条件を抜き出す復習をかねてやっておきましょう。
（３） Ａ，Ｂ ２種類のジュースがある。
Ａ\(\,3\,\)本とＢ\(\,1\,\)本の代金は\(\,1300\,\)円で，Ａ\(\,2\,\)本とＢ\(\,3\,\)本の代金は\(\,1450\,\)円である。
Ａ\(\,1\,\)本，Ｂ\(\,1\,\)本の値段をそれぞれ求めよ。
２．（２）までは別のページにあります。
ここにはありませんので気にしないでください。
⇒ 連立方程式の文章問題を解くポイント(十の位一の位の数を入れかえる)
求めたいものはＡとＢの\(\,1\,\)本の値段なので、
Ａ\(\,1\,\)本の値段を \(x\) ，Ｂ\(\,1\,\)本の値段を \( y\) とします。
後は問題の条件通りに式を２つ立てればいいだけです。
『Ａ\(\,3\,\)本とＢ\(\,1\,\)本の代金は\(\,1300\,\)円』から
\( 3x+y=1300 ･･･①\)
『Ａ\(\,2\,\)本とＢ\(\,3\,\)本の代金は\(\,1450\,\)円』から
\( 2x+3y=1450 ･･･②\)
①②を連立させると、
\( \begin{cases} 3x+y=1300 \\ \\ 2x+3x=1450 \end{cases}\)
これを解いて
\( x=350 , y=250\)
（計算は自分でしてみてください。）
答えはそのままです。
Ａ\(\,1\,\)本の値段は\(\,350\,\)円
Ｂ\(\,1\,\)本の値段は\(\,250\,\)円。
次は少しレベルを上げてみましょう。
といってもそれほど変わりませんが苦手にしている人が多い速さの問題や食塩水の問題をやって見ます。
速さの問題の解き方
文章題の基本は、「求めたいもの、分からないものを文字でおく」、これは同じです。
（１） Ａ，Ｂの２人が，水泳とマラソンだけのトライアスロンをした。
Ａは分速\(\,50\,\)ｍで泳ぎ，分速\(\,150\,\)ｍで走って\(\,2\,\)時間かかった。
Ｂは分速\(\,40\,\)ｍで泳ぎ，分速\(\,200\,\)ｍで走って，\(\,1\,\)時間\(\,40\,\)分かかった。
２人は，水泳，マラソンそれぞれ何ｍのトライアスロンをしたか求めよ。
「道のり」と「速さ」と「時間」の関係は、
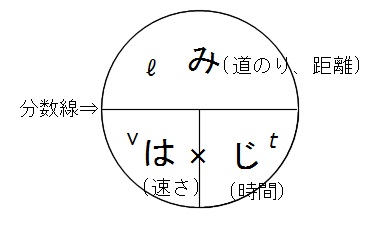
「道のり」＝「速さ」×「時間」
「速さ」＝「道のり」÷「時間」
「時間」＝「道のり」÷「速さ」
です。
例えば
「みちのり」を知りたければ \(「は」\times 「じ」\)
「はやさ」を知りたければ \(\displaystyle \frac{「み」}{「じ」}\)
「じかん」を知りたければ \(\displaystyle\frac{「み」}{「は」}\)
で式にします。
求めたいのは、水泳の「道のり」と、マラソンの「道のり」です。
水泳の道のりを \(x\) (ｍ)
マラソンの道のりを \( y\) (ｍ) とおきます。
さて、分かっているのは、「速さ」です。
時間は水泳とマラソンとの合計での時間なので、
それぞれにかかった時間は分かっていません。
線分図１つで大きく変わる
そこで、線分図を書いてみましょう。
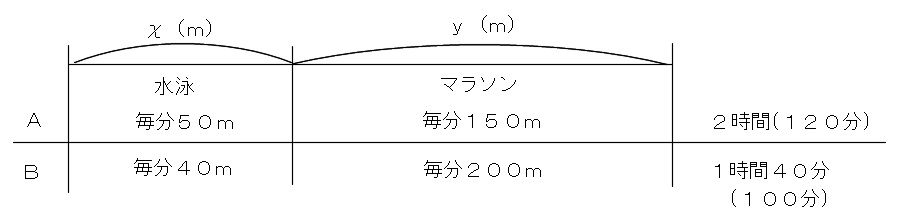
この線分図を書くのと書かないのとでは大きな差になりますよ。
速さが分速なので、時間の単位をを分に換えておくことに注意して、
Ａ：「水泳にかかった時間」と「マラソンでかかった時間」とを足すと\(\,120\,\)分
Ｂ：「水泳にかかった時間」と「マラソンでかかった時間」とを足すと\(\,100\,\)分
の関係を式にすると、
Ａ： \(\displaystyle \frac {x}{50}+ \frac{y}{150}=120\) ･･･①
Ｂ： \(\displaystyle \frac {x}{40}+ \frac{y}{200}=100\) ･･･①
①②を連立させて解けばいいだけですが、分数があるので分母を無くします。
①は全体を\(\,150\,\)倍、②は全体を\(\,200\,\)倍します。
最小公倍数が計算は一番楽になりますが、公倍数なら何でも良いです。
とにかく分数を無くすことで計算しやすくします。
すると、
\( \begin{cases} 3x+y=18000 \\ \\ 5x+y=20000 \end{cases}\)
という連立方程式になります。
これを解くと、
\( x=1000 , y=15000\) となります。
答えは、
\(\underline{\,水泳 1000 ｍ\,}\)
\(\underline{\,マラソン 15000 ｍ\,}\)
このように、道のり、速さ、時間に関する問題はどういう関係が成り立つか、
どれを方程式にするか、それを探せばいいだけです。
左辺は時間、右辺は道のり、なんてことはありません。
速さや道のりの関係式は３つしか無いのだから、どれかですよ。
このうちどれかを使って関係式を２つ作る。
そして、それを解くだけです。
連立方程式の処理は復習しておきましょう。
⇒ 小数や分数が係数にある連立方程式をはやく解く解き方のコツ
文章問題は立式してしまえば、計算処理は簡単なのものが多いですからね。
長くなりそうなので食塩水の問題は別に解説することにします。
⇒ 連立方程式(食塩水の濃度と食塩水を混ぜる文章問題の立式方法と解き方)
理科でも必要になるので解ける様になっておきましょう。
比例計算ができれば理解でも計算問題に強くなれます。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
