和歌山県公立高校入試2021年（令和3年）度数学の問題と解説

2021年（令和3年）度の和歌山県公立高校入試数学の問題と解説です。
例年通りかたよりの無い中学数学全般の基礎の確認問題と
若干の応用を必要とする標準的な問題で構成されています。
高得点を狙う場合の対策も基礎の抜け落ちがないかの確認がポイントになります。

和歌山県公立高校入試2021年（令和3年）度数学の問題

令和３年度の問題も大問５つで例年通りです。

⇒　和歌山県公立高校入試2021年（令和3年）度数学の問題

和歌山の県立入試では除外された項目はありません。

和歌山県公立高校入試2021年（令和3年）度数学の解説

基本問題中心なので解説も簡単に済ませておきます。
大問は５つですが小問に分かれる問題もあり、
問題数が多いので時間配分に注意が必要ですね。

第１問小問集合

\(\color{black}{\fbox{1}}\)
〔問１〕から〔問５〕まであります。

〔問１〕計算問題が５題です。
(1)
　\(\hspace{10pt}3-7\\
=\underline{　-4　}\)

数直線上で\(\,3\,\)から
左に\(\,7\,\)移動します。

(2)
　\(\hspace{10pt}\displaystyle -1+4\div \frac{2}{3}\\
\displaystyle =-1+4\times \frac{3}{2}\\
=-1+6\\
=\underline{　5　}\)

割り算は分数でも逆数の掛け算です。

(3)
文字式の展開です。

　\(\hspace{10pt}3(2a+5b)-(a+2b)\\
=6a+15b-a-2b\\
=\underline{　5a+13b　}\)

文字式も計算順序などの規則は同じです。

(4)
無理数の計算です。

　\(\hspace{10pt}\displaystyle \frac{10}{\sqrt{2}}-\sqrt{8}\\
\displaystyle =\frac{10\sqrt{2}}{2}-2\sqrt{2}\\
=5\sqrt{5}-2\sqrt{2}\\
=\underline{　3\sqrt{2}　}\)

分母の有理化と素因数分解は確実に進めましょう。

(5)
文字式の展開です。

　\(\hspace{10pt}(x-2)(x+2)+(x-1)(x+4)\\
=(x^2-4)+(x^2+3x-4)\\
=x^2-4+x^2+3x-4\\
=\underline{　2x^2+3x-8　}\)

展開公式を使わなくても、
確実に展開していけば良いですよ。

⇒　高校入試対策 中学数学単元別の要点とまとめ

基本が不十分と感じる人は確認しておきましょう。

〔問２〕
２次方程式を解きます。
　\(\hspace{4pt}x^2+5x+3=0\)

因数分解できないので解の公式です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{5^2-4\cdot (1)\cdot (3)}}{2\times 1}\\
&=&\frac{-5\pm \sqrt{25-12}}{2}\\
&=&\frac{-5\pm \sqrt{13}}{2}
\end{eqnarray}\)

２次方程式の解の公式は使えることが先で良いです。
解の公式を使えばすべての２次方程式が解けますが
因数分解できるかを先に試してからですよ。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

公式は導けなくても良いですが
使えるようにはなっておきましょう。

〔問３〕
等式の変形です。
　\(\begin{eqnarray}\displaystyle
4x+3y-8&=&0\\
3y&=&8-4x\\
y&=&\underline{\underline{　\frac{8-4x}{3}　}}
\end{eqnarray}\)

分母を分けて
　\(\hspace{10pt}\displaystyle y=-\frac{4}{3}\,x+\frac{8}{3}\)
でも良いですよ。

〔問４〕
不等号を使って表す問題です。

小数第１位を四捨五入して14になるのは
　「\(\,13.5\,\)以上」で「\(\,14.5\,\)より小さい数」
なので
　\(\hspace{4pt}\underline{　13.5\,≦\,a\,＜\,14.5　}\)

\(\,14.5\,\)は四捨五入すると\(\,15\,\)になるので含みません。

〔問５〕
中央値と最頻値を求めます。

データが小さい順に並べてあるので
並べ直す必要がありません。

中央値は左から\(\,5\,,\,6\,\)番目の平均値になります。
（右からでも同じ）
　\(\hspace{10pt}\displaystyle \frac{20+22}{2}=\underline{　21　}\)

最頻値は度数が最も多い値です。
　\(\hspace{10pt}\underline{　17　}\)

代表値は意味が分からないと答えられません。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

意味さえ知ってしまえばデータを並べ直すだけで
計算は簡単なものが多いです。

第２問小問集合

\(\color{black}{\fbox{2}}\)
空間の位置関係から確率や方程式など
〔問１〕から〔問４〕までの４問があります。

〔問１〕
立方体について３題あります。
(1)
辺\(\,\mathrm{AB}\,\)と垂直な面を１つ答えます。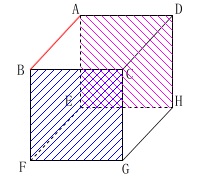２つありますが１つで良いです。

答え　\(\,\underline{　\mathrm{面\,BFGC}　}\,\)または\(\,\underline{　\mathrm{面\,AEHD}　}\,\)

(2)
辺\(\,\mathrm{AD}\,\)とねじれの位置にある辺を数えます。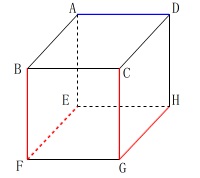
答え　\(\,\underline{　4　}本\,\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

ねじれの位置にある辺について
注意しておかなければならないことがあります。
良く問題になるので確認しておきましょう。

(3)
点と直線との距離の問題です。

「距離」は最短距離のことなので垂線になります。
ここでは辺\(\,\mathrm{AH}\,\)の長さが距離です。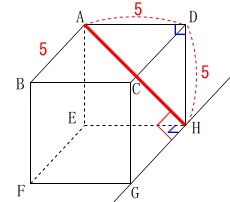\(\,\mathrm{△ADH}\,\)は三角定規なので
　\(\hspace{10pt}\mathrm{AH}=\underline{　5\sqrt{2}　}\mathrm{cm}\)

もちろん三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AH}&=&\sqrt{5^2+5^2}\\
&=&\sqrt{50}\\
&=&5\sqrt{2}
\end{eqnarray}\)
でも良いです。

〔問２〕
条件にあてはまる関数を選びます。

条件
　\(\,x＞0\,\)の範囲で
　\(\,x\,\)の値が増加するにつれて
　\(\,y\,\)の値が減少する。

グラフを簡単にでも良いのでかいて、
\(\,y\,\)軸より右側で右に行くほど
\(\,y\,\)が減少しているものを選べば良いです。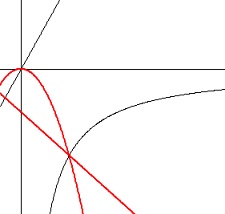
答え　
　\(\hspace{4pt}\underline{　ウ　}　y=-x-2\)
　\(\hspace{4pt}\underline{　エ　}　\displaystyle y=-x^2\)

〔問３〕
規則によって動く点の確率問題です。

「規則」で注意するのは
１回目に\(\,\mathrm{A}\,\)に止まったときは
２回目は取り出したカードの数字より１大きく動かす。
ということです。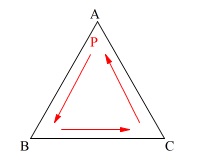１回目に取り出したカードは元にもどし、
まわる方向は反時計回りです。

(1)
\(\,1\,\)回目の移動後に\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)にある確率です。

最初\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)にあるので、
\(\,\mathrm{B}\,\)に移動するのは
　\(\,\color{black}{\fbox{1}}\,,\,\color{black}{\fbox{4}}\,\)のカードを取り出したとき
なので
　\(\hspace{4pt}\displaystyle \frac{2}{4}=\underline{　\frac{1}{2}　}\)

(2)
２回の移動で\(\,\mathrm{P}\,\)が\(\,\mathrm{C}\,\)の位置にある確率です。

あれこれ考えるより樹形図の方が早いです。
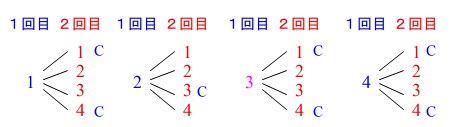１回目に\(\color{black}{\fbox{3}}\)を取り出したとき
\(\,2\,\)回目は取り出したカードに\(\,+1\,\)することに注意して
　\(\hspace{4pt}\displaystyle \underline{　\frac{7}{16}　}\)

取り出したカードの数字の合計が
\(\,\color{magenta}{2}\,,\,\color{blue}{5}\,,\,\color{red}{8}\,\)になるときですが、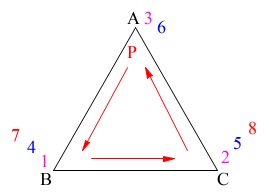\(\,1\,\)回目が\(\color{black}{\fbox{3}}\)のときは
合計に\(\,+1\,\)されます。

〔問４〕
道のり、速さ、時間の問題です。

午後\(\,4\,\)時に学校を出発し、
学校から家までは毎分\(\,\mathrm{80\,m}\,\)で、
家に到着して\(\,5\,\)分後に
自転車で図書館に毎分\(\,\mathrm{240\,m}\,\)、
午後\(\,4\,\)時\(\,18\,\)分に学校から\(\,\mathrm{2000\,m}\,\)離れた図書館に到着。
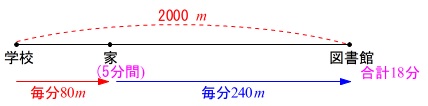ということが問題に書いてあります。
※
単位をそろえておきたいので\(\,m\,\)にしてあります。

距離か時間を文字でおく方法がありますが、
求めたいのは時間なので
家を出発した時刻を\(\,4\,\)時\(\,x\,\)分とします。

\(\,5\,\)分間家にいたので学校から家まで歩いた時間は
　\(\hspace{4pt}(\color{red}{x-5})\,分\)
また家から図書館まで歩いた時間は
　\(\hspace{4pt}(\color{blue}{18-x})\,分\)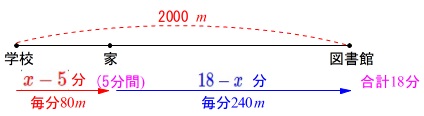移動した距離は\(\,2000\,\)なので
　\(\hspace{4pt}80(x-5)+240(18-x)=2000\)
これを解いて
　\(\hspace{10pt}x=12\)

答え　\(\,4\,時\underline{　12　}分\,\)

学校を出発してからの時間を文字で表しても良いですし、
連立方程式にしても良いです。

答えるのは何かをしっかり読み取っていれば何でも良いです。

第３問規則性

\(\color{black}{\fbox{3}}\)
規則性の問題が〔問１〕〔問２〕とあります。

考え方は色々ありますが
問題が解き方を説明してくれているので
長い文章を読み取るだけです。

〔問１〕
白タイルと黒タイルの枚数の関係です。

タイルの枚数の表があります。
\(\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline
番目 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\ \hline
白 & 1 & \color{magenta}{3} & \color{blue}{6} & \color{red}{10} & 15 & \color{black}{\fbox{ア}} & * & * \\ \hline
黒 & 0 & 1 & \color{magenta}{3} & \color{blue}{6} & \color{red}{10} & * & * & \color{black}{\fbox{イ}}\\ \hline
計 & 1 & 4 & 9 & 16 & 25 & * & * & *\\ \hline
\end{array}\)

(1)
６番目の白と８番目の黒の枚数を答えます。

規則によると６番目の白は
５番目の白より６枚多くなるので
　答え　\(\,ア　\underline{　21　}\,\)　

８番目の黒は７番目の白と同じです。
６番目の白は\(\,21\,\)なので
７番目の白は
　\(\hspace{4pt}21+7=28\)

答え　\(\,イ　\underline{　28　}\,\)

図を書き上げてでもここは出しておきたいですね。
図で考えると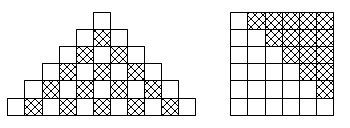と見ることもできます。
（この形は色々考えられます。）

白黒ともに１つずつ増えていくので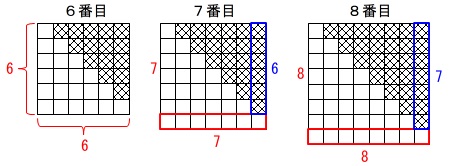６番目の白タイルの数は
　\(\hspace{4pt}1+2+3+\cdots +6=21\)

８番目の黒タイルの数は
　\(\hspace{4pt}1+2+3+\cdots +7=28\)

正方形なので白黒合わせると
平方数になることが(2)で利用されています。

※
表の数字だけから規則性を見ることは十分できます。
時間をかけていられない試験会場では
数字を追いかけた方が早いですよ。

(2)
\(\,n\,\)番目の白タイルの枚数を\(\,n\,\)を使って表します。

白と黒のタイルの枚数や
「合計の枚数が平方数になる」
ことは問題が書いてくれているので
流れにのって文字式を処理するだけです。

（\(\,n\,\)番目のタイルの合計枚数を\(\,n\,\)の式で表すと）
\(\,n\,\)の平方数\(\,n^2\,\)となる。
これが白と黒のタイルの合計になるから
　\(\begin{eqnarray}\displaystyle
x+(x-n)&=&n^2\\
2x&=&n^2+n\\
x&=&\frac{n^2+n}{2}\\
&=&\frac{1}{2}n(n+1)
\end{eqnarray}\)

\(\,n\,\)番目の白タイルの枚数
　\(\hspace{4pt}\underline{　\displaystyle \frac{1}{2}n(n+1)　}枚\)

表の数字から
白タイルの枚数の「増え方」が
　\(\hspace{4pt}+2\,,\,+3\,,\,+4\,,\,\cdots\)
となっていることが分かれば表の中がうまるので
後は文字式を処理するだけですね。

〔問２〕
今度は周の長さについての問題ですが、
和歌子さんが素晴らしい着目をしているので簡単です。

ここでも表があるので数字を見ていけば解決します。
　\(\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline
番目 & 1 & 2 & 3 & 4 & \cdots & ☆ & ★ & \cdots \\ \hline
周 & 4 & 10 & 16 & 22 & \cdots & a & b & \cdots \\ \hline
\end{array}\)

(1)
周の長さは\(\,6\,\)ずつ増えていくので
　\(\hspace{4pt}\underline{　b-a=6　}\)

タイルを合わせた図形の周の長さは
図形を囲む長方形になる。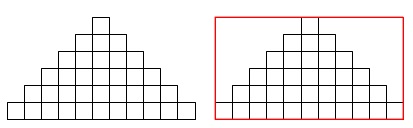和歌子さんの着目した周の長さです。

１つ前の番目の図形と比べてみると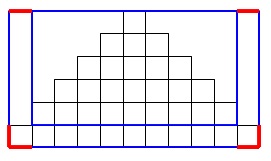長くなっている\(\,\color{red}{6}\,\)の部分が分かります。
（関係ないけど。）

和歌子さんの着目した長方形の周の長さを利用します。

\(\,n\,\)番目の長方形の縦と横の長さを
\(\,n\,\)を使って表すことを考えます。

縦には\(\,\color{red}{n}\,\)個並び、
横には「\(\,n\,\)番目の奇数」分\(\,\color{blue}{2n-1}\,\)個並ぶ。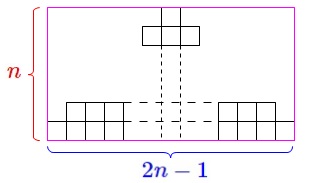よって\(\,n\,\)番目の周の長さは
（上下、左右を考えて）
　\(\hspace{10pt}2\times \color{red}{n}+2\times (\color{blue}{2n-1)}\\
=2\,n+4\,n-2\\
=6\,n-2\)
と表されるので\(\,50\,\)番目の図形の周の長さは
　\(\hspace{10pt}6\times (50)-2\\
=\underline{　298　}\mathrm{cm}\)

長方形を利用せず数字だけを見てくと
\(\,n\,\)番目の周の長さは
\(\,1\,\)番目の\(\,4\,\)から\(\,(n-1)\,\)回分\(\,\color{red}{6}\,\)増えるので
　\(\hspace{4pt}4\color{red}{+6+6+\cdots +6}\)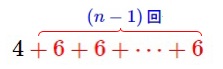
　\(\hspace{10pt}4+6\times (n-1)\\
=6n-2\)
とした方が早い、と感じた人も多いでしょう。

「和歌子さんの考え方を参考にして」
とはありますが解法を示すわけではないので
どちらでも構いませんよ。

第４問正方形上の動点

\(\color{black}{\fbox{4}}\)
正方形の周上を２点が移動する問題です。

２点の移動する速さが違いますが
問題の順に進めれば分かり易くなっています。

問題全体に通じる条件がありますので整理しておきます。
※
長さの単位は\(\,\mathrm{cm}\,\)です。

条件
　\(\,\mathrm{O\,(\,0\,,\,0\,)}\,\)\(\,\mathrm{A\,(\,6\,,\,0\,)}\,\)
　\(\,\mathrm{B\,(\,6\,,\,6\,)}\,\)\(\,\mathrm{C\,(\,0\,,\,6\,)}\,\)
　\(\,\mathrm{P\,,\,Q}\,\)は\(\,\mathrm{O}\,\)を出発点とし
　\(\,\mathrm{P}\,\)は毎秒\(\,\mathrm{3}\,\)の速さで
　\(\,\mathrm{O\rightarrow C\rightarrow B\rightarrow A}\,\)の順に\(\,\mathrm{A}\,\)まで
　\(\,\mathrm{Q}\,\)は毎秒\(\,\mathrm{1}\,\)の速さで
　\(\,\mathrm{O\rightarrow A}\,\)の順に\(\,\mathrm{A}\,\)まで動く。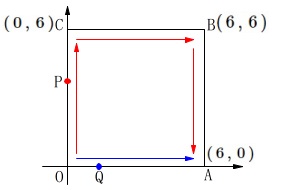
〔問１〕
\(\,\mathrm{P\,,\,Q}\,\)がそれぞれ\(\,\mathrm{A}\,\)に到着するのは何秒後かです。

\(\,\mathrm{P}\,\)は毎秒\(\,3\,\)で正方形の\(\,3\,\)辺（\(\,18\,\)）を移動するので
　\(\hspace{4pt}\displaystyle \frac{18}{3}=\underline{　6　}秒後\)

\(\,\mathrm{Q}\,\)は毎秒\(\,1\,\)で正方形の\(\,1\,\)辺（\(\,6\,\)）を移動するので
　\(\hspace{4pt}\displaystyle \frac{6}{1}=\underline{　6　}秒後\)

〔問２〕
\(\,\mathrm{P\,,\,Q}\,\)が出発して１秒後の
直線\(\,\mathrm{PQ}\,\)の式を求めます。

１秒後の座標は
　\(\hspace{4pt}\mathrm{P}\,(0\,,\,3\,)\)
　\(\hspace{4pt}\mathrm{Q}\,(1\,,\,0\,)\)

\(\,2\,\)点\(\,\mathrm{P\,,\,Q}\,\)を通る直線の式は
　\(\hspace{10pt}\underline{　y=-x+3　}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

本格的な関数問題では直線の式をいくつも求めることがあるので、
２点を通る直線の式は短時間で求められるようになっておいた方が良いですよ。

〔問３〕
\(\,\mathrm{△APQ}\,\)が二等辺三角形になる問題です。

\(\,\mathrm{PO=PQ}\,\)の場合だけなので簡単です。
（\(\,\mathrm{OQ=PQ}\,\)を考えなくて良い。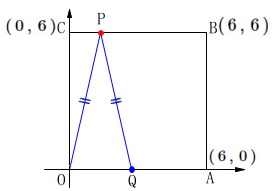）　\(\hspace{4pt}\mathrm{PO=PQ}\)
となるのは線分\(\,\mathrm{CB}\,\)上しかありません。

出発してから\(\,t\,\)秒後の座標を
　\(\hspace{4pt}\mathrm{Q}\,(\,\color{blue}{t}\,,\,0\,)\)
とすると\(\,\mathrm{P}\,\)は\(\,3\,t\,\)移動し
線分\(\,\mathrm{CB}\,\)上にあるとして良いので
　\(\hspace{4pt}\mathrm{P}\,(\,\color{red}{3t-6}\,,\,6\,)\)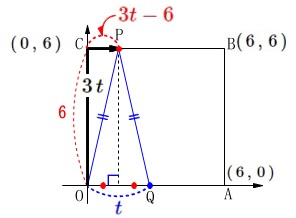\(\,\mathrm{PO=PQ}\,\)の二等辺三角形なので
\(\,x\,\)座標を比較して
　\(\begin{eqnarray}\displaystyle
\mathrm{OQ}&=&2\,\mathrm{CP}\\
t&=&2\times (3t-6)\\
-5t&=&-12\\
t&=&\underline{　\frac{12}{5}　}秒後
\end{eqnarray}\)

点\(\,\mathrm{Q}\,\)の座標を\(\,(\,t\,,\,0\,)\)とすると
\(\,x\,\)座標が半分になることから
点\(\,\mathrm{P}\,\)の座標を\(\displaystyle \mathrm{P}\,\left(\frac{t}{2}\,,\,6\,\right)\)
として\(\,\mathrm{P}\,\)の移動距離を考えて
　\(\begin{eqnarray}\displaystyle
\frac{t}{2}+6&=&3\,t\\
t&=&\frac{12}{5}
\end{eqnarray}\)
でも良いですよ。

〔問４〕
\(\,\mathrm{P\,,\,Q}\,\)が出発して５秒後の面積です。

５秒後の点の座標はそれぞれ
　\(\,\mathrm{P\,(\,6\,,\,3\,)}\,\)
　\(\,\mathrm{Q\,(\,5\,,\,0\,)}\,\)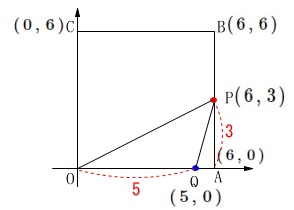このとき\(\,\mathrm{△OPQ}\,\)の面積は
底辺を線分\(\,\mathrm{OQ}\,\)、高さを\(\,\mathrm{AP}\,\)と見ることができるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△OPQ}&=&\frac{1}{2}\times \mathrm{OQ}\times \mathrm{AP}\\
&=&\frac{1}{2}\times 5\times 3\\
&=&\color{red}{\frac{15}{2}}
\end{eqnarray}\)

線分\(\,\mathrm{AP}\,\)上の点\(\,\mathrm{D}\,\)とでできる
\(\,\mathrm{△OPD}\,\)は高さが\(\,\color{magenta}{6}\,\)とみることができ
\(\,\mathrm{△OPQ}\,\)と面積が等しくなるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△OPQ}&=&\mathrm{△OPD}\\
\color{red}{\frac{15}{2}}&=&\frac{1}{2}\times \mathrm{PD}\times \color{magenta}{6}\\
15&=&6\times \mathrm{PD}\\
\mathrm{PD}&=&\color{blue}{\frac{5}{2}}
\end{eqnarray}\)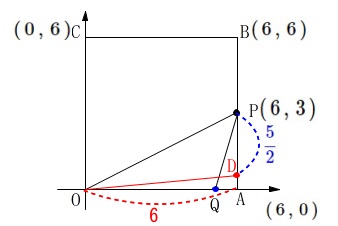このとき\(\,\mathrm{AD}\,\)は
　\(\begin{eqnarray}\displaystyle
\mathrm{AD}&=&\mathrm{AP-PD}\\
&=&3-\frac{5}{2}\\
&=&\frac{1}{2}
\end{eqnarray}\)
これは\(\,\mathrm{D}\,\)の\(\,y\,\)座標になります。
（\(\,x\,\)座標は\(\,6\,\)です。）

よって\(\,\mathrm{D}\,\)の座標は
　\(\hspace{4pt}\displaystyle \underline{　\mathrm{D}\,\left(\,6\,,\,\frac{1}{2}\,\right)　}\)

底辺を\(\,\mathrm{OP}\,\)と見て、
頂点\(\,\mathrm{Q}\,\)を平行移動しても良いのですが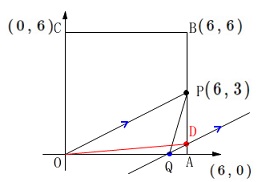具体的に面積を出す方向で進めました。

直線\(\,\mathrm{QD}\,\)の式は
　\(\hspace{4pt}\displaystyle y=\frac{1}{2}\,x-\frac{5}{2}\)
です。

第５問平面図形（円周角と相似）

\(\color{black}{\fbox{5}}\)
円周上に\(\,4\,\)点\(\,\mathrm{A\,,\,B\,,\,C\,,\,D}\,\)があります。
各問題で条件が変わるので注意しておきましょう。

〔問１｝
角度を求めます。

条件
　\(\,\mathrm{DB=DC}\,\)
　\(\,\mathrm{∠BDC=70^{\circ}}\,\)
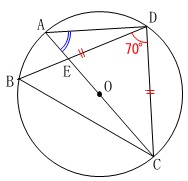\(\,\mathrm{∠CAD}\,\)を求めます。

\(\,\mathrm{△DBC}\,\)は二等辺三角形で
頂角が\(\,\mathrm{∠BDC=70^{\circ}}\,\)なので
　\(\displaystyle \mathrm{∠CBD}=\frac{180^{\circ}-70^{\circ}}{2}=\color{blue}{55^{\circ}}\)

1つの弧\(\,\mathrm{DC}\,\)の円周角は等しいので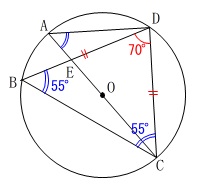
　\(\begin{eqnarray}\displaystyle
\mathrm{∠CAD}&=&\mathrm{∠CBD}\\
&=&\underline{　55　}(度)
\end{eqnarray}\)

〔問２〕
条件が変わります。

条件
　\(\,\mathrm{AC=4}\,\)
　\(\,\mathrm{∠ACD=30^{\circ}}\,\)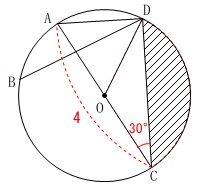斜線部分の面積を求めます。

中心角\(\,\mathrm{∠DOC}\,\)のおうぎ形から
\(\,\mathrm{△ODC}\,\)（二等辺三角形）を引けば求まります。

\(\,\mathrm{△DOC}\,\)は二等辺三角形なので
　\(\,\mathrm{∠DOC=\color{blue}{120^{\circ}}}\,\)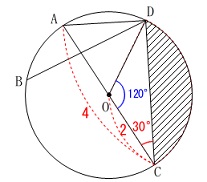また\(\,\mathrm{AC}\,\)は直径なので
　\(\,\mathrm{∠ADC=90^{\circ}}\,\)　
三角定規の比から
　\(\hspace{10pt}\mathrm{DC}=\color{red}{2\sqrt{3}}\)
中心\(\,\mathrm{O}\,\)から\(\,\mathrm{DC}\,\)に垂線\(\,\mathrm{OH}\,\)を引くと
　\(\hspace{4pt}\mathrm{OH}=1\)
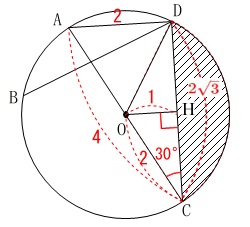よって求める面積\(\,Sは\,\)
　\(\begin{eqnarray}\displaystyle
S&=&\pi\,(2)^2\times \frac{120}{360}-\frac{1}{2}\times 2\sqrt{3}\times 1\\
&=&\underline{　\frac{4}{3}\,\pi-\sqrt{3}　}\mathrm{cm^2}
\end{eqnarray}\)

〔問３〕
辺の長さが等しいことの証明です。

条件
　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{DF}\,\)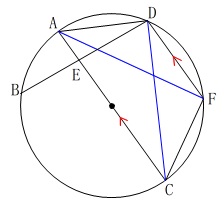このとき
　\(\hspace{4pt}\mathrm{ＡＦ=ＣＤ}\)
を証明します。

具体的な長さがないので合同の利用ですね。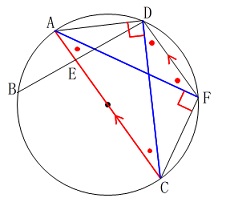
　\(\,\mathrm{△AFC}\,\)と\(\,\mathrm{△CDA}\,\)において
平行線の錯角は等しいから
　\(\hspace{4pt}\mathrm{\color{red}{∠AFD}=∠FAC}　･･･①\)
円周角の定理から
　\(\hspace{4pt}\mathrm{\color{red}{∠AFD}=∠DCA}　･･･②\)
\(\,①②\,\)から
　\(\hspace{4pt}\mathrm{∠FAC=∠DCA}　･･･③\)
\(\,\mathrm{AC}\,\)は直径で共通な辺なので
　\(\hspace{4pt}\mathrm{AC=CA}　･･･④\)
　\(\hspace{4pt}\mathrm{∠AFC=∠CDA}=90^{\circ}　･･･⑤\)
\(\,③④⑤\,\)より
　直角三角形の斜辺と１つの鋭角がそれぞれ等しい。
よって
　\(\,\mathrm{△AFC}\,\)≡\(\,\mathrm{△CDA}\,\)
合同な図形の対応する辺は等しいので
　\(\hspace{10pt}\mathrm{ＡＦ=ＣＤ}\)
（終わり）

注意するのは、
合同の証明で終わらないことですね。

〔問４〕
面積比を求める問題です。

条件
　\(\,\mathrm{AC⊥BD}\,\)
　\(\,\mathrm{AD=3\,,\,DE=\sqrt{5}}\,\)
　\(\,\mathrm{BA}\,\)∥\(\,\mathrm{CF}\,\)
※
長さの単位は\(\,\mathrm{cm}\,\)です。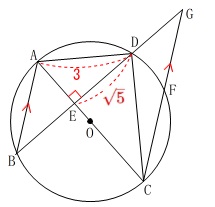\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△CGE}\,\)の面積比です。

具体的な面積も求めることができるので
解法をいくつか用意してくれているのでしょう。

ここでは合同と相似を利用して面積比を出しておきます。

その前に直角三角形の\(\,2\,\)辺が分かっているので
\(\,\mathrm{△ADE}\,\)において三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AE^2+DE^2}&=&\mathrm{AD^2}\\
\mathrm{AE^2}+(\sqrt{5})^2&=&3^2\\
\mathrm{AE^2}&=&4\\
\mathrm{AE}&=&\pm 2
\end{eqnarray}\)
\(\,\mathrm{AE}\,\)は長さだから\(\,\mathrm{AE＞0}\,\)で
　\(\hspace{10pt}\mathrm{AE}=\color{red}{2}\)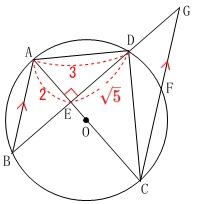
　\(\,\mathrm{AC⊥BD}\,\)
　\(\,\mathrm{BA}\,\)∥\(\,\mathrm{CF}\,\)
からまとめて条件を書き出すと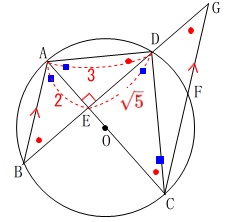合同と相似な図形がたくさんあります。

どれを使っても同じようなものなので
相似な三角形
　\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△CGE}\,\)
の比から面積比を求めることにします。

相似比は\(\,\mathrm{AE:CE}\,\)です。
　\(\,\mathrm{△AED}\,\)∽\(\,\mathrm{△DEC}\,\)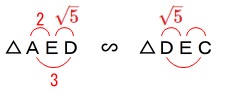なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AE:DE}&=&\mathrm{ED:EC}\\
2:\sqrt{5}&=&\sqrt{5}:\mathrm{EC}\\
2\times \mathrm{EC}&=&5\\
\mathrm{EC}&=&\color{blue}{\frac{5}{2}}
\end{eqnarray}\)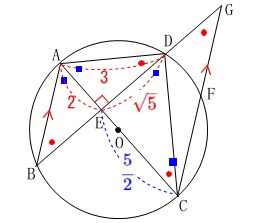このことから\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△CGE}\,\)の相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{AE:CE}&=&2:\frac{5}{2}\\
&=&4:5
\end{eqnarray}\)

よって面積比は
　\(\hspace{10pt}4^2:5^2=\underline{　16:25　}\)
※
相似比\(\,\color{red}{a}:\color{blue}{b}\,\)のとき
面積比は\(\,\color{red}{a^2}:\color{blue}{b^2}\,\)です。

具体的な面積を求めると
　\(\hspace{4pt}\displaystyle \mathrm{△ABE}=\sqrt{5}\)
　\(\hspace{4pt}\displaystyle \mathrm{△CGE}=\frac{25\sqrt{5}}{16}\)
となるので
　\(\hspace{10pt}\displaystyle
\mathrm{△ABE:△CGE}\\
\displaystyle =\sqrt{5}:\frac{25\sqrt{5}}{16}\\
=\underline{　16:25　}\)

簡単なので面積計算は自分でやってみて下さい。

以上です。

ここは対策ページではないので細かくはいいませんが、
問題自体は基本中心です。
ただ、改めて見ると「多いわっ！」
って受験生は（解説する私も）感じる量です。
広い範囲の基本をすぐに引き出せるように、
徹底して習得おくことが一番の対策になります。
（どこでも同じですけど、より重視して。）

⇒　和歌山県公立高校入試の数学の過去問題と解答解説

基本さえおさえておけば試験時間は十分余ります。