令和3年（2021年）度奈良県公立高校入試数学の問題と解説

令和3年（2021年）度の奈良県公立高校入試の数学の問題と解説です。
大問4つの構成は前年度と同じで、
中学で学習する数学すべてを問いに組み込んでいるといって良いでしょう。
問題自体はシンプルに書かれていますが
問題量は少なくないので取り組み方で差が出る問題です。

令和3年（2021年）度奈良県公立高校入試数学の問題

2021年度の奈良県の県立入試では除外項目はほぼありません。
※
「標本調査」は除外されていますが過去問として影響はありません。

⇒　令和3年（2021年）度奈良県公立高校入試数学の問題

小問集合、関数、図形総合問題など大問が４問あります。

令和3年（2021年）度奈良県公立高校入試数学の解説

問題量が結構あるので早速解説に入ります。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
(1)から(8)まであり、
さらに問題が分かれるものもあります。

(1)
計算問題が4つあります。

①
　\(\hspace{10pt}-2-5\\
=\underline{　-7　}\)

数直線上で\(\,-2\,\)から左に\(\,5\,\)移動します。

②
　\(\hspace{10pt}-3^2\times 9\\
=-9\times 9\\
=\underline{　-81　}\)

符号のミスに注意ですね。
\(\,-3^2=-(\,3\times 3)\,\)です。

③
　\(\hspace{10pt}8a^2b\div (-2ab)^2\times 6ab\\
\displaystyle =\frac{8a^2b\times 6ab}{4a^2b^2}\\
=\underline{　12a　}\)

割り算は逆数の掛け算です。

④
　\(\hspace{10pt}(x+7)(x-4)-(x-4)^2\\
=(x^2+3x-28)-(x^2-8x+16)\\
=x^2+3x-28-x^2+8x-16\\
=\underline{　11x-44　}\)

３行目の（かっこ）を外す一行を書くことで
計算ミスを減らせます。

(2)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 3x+4y=1　･･･①\\
\hspace{4pt} 2x-y=-3　･･･②
\end{cases}\)

ここでは\(\,y\,\)を消去する方向で進めます。
\(\,(①+4\times ②)\,\)から
　\(\hspace{14pt}3x+4y=1\\
\underline{+)\,8x-4y=-12}\\
\hspace{8pt}11x\hspace{21pt}=-11\\
\hspace{40pt}x=-1\)

\(\,②\,\)から
　\(\begin{eqnarray}\displaystyle
2x-y&=&-3\\
y&=&2x+3\\
&=&2\times (-1)+3\\
&=&1
\end{eqnarray}\)

答え　\(\,\underline{　x=-1\,,\,y=1　}\,\)

連立方程式は一文字消去が基本です。

(3)
２次方程式を解きます。
　\(\hspace{4pt}x^2-3x+1=0\)

左辺の因数分解ができないので
解の公式を利用します。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{3\pm \sqrt{(-3)^2-4\cdot (1)\cdot (1)}}{2\times 1}\\
&=&\frac{3\pm \sqrt{9-4}}{2}\\
&=&\underline{\underline{　\frac{3\pm \sqrt{5}}{2}　}}
\end{eqnarray}\)

⇒　２次方程式を解の公式で解く問題の見分け方と例題

解の公式は使えるようになっておきましょう。

(4)
無理数の小数部分と文字式の計算です。

　\(\hspace{4pt}\sqrt{9}＜\sqrt{15}＜\sqrt{16}\)
なので
　\(\hspace{4pt}3\,＜\,\sqrt{15}\,＜\,4\)
だから
　\(\hspace{10pt}\sqrt{15}=3.\cdots\)
小数部分\(\,a\,\)は整数部分を引いて
　\(\hspace{10pt}a=\sqrt{15}-3\)

ここからは代入しても良いですが
会員は代入しない方法で解いているはずです。

　\(\begin{eqnarray}\displaystyle
a&=&\sqrt{15}-3\\
a+3&=&\sqrt{15}
\end{eqnarray}\)
両辺を２乗して
　\(\begin{eqnarray}\displaystyle
(a+3)^2&=&(\sqrt{15})^2\\
a^2+6a+9&=&15\\
a^2+6x&=&\underline{　6　}
\end{eqnarray}\)

時間かかけるけど、
二次式程度なので代入しても良いですよ。

(5)
データから読み取れる適切なものをすべて選びます。

ア
\(\,5\,\)時間以上\(\,6\,\)時間未満の階級では度数は同じです。
度数合計が\(\,\mathrm{B}\,\)の方が多いので
\(\,\mathrm{A}\,\)の方が相対度数は大きい。
○

イ
\(\,8\,\)時間以上の生徒数は同じ。
×

ウ
最頻値は同じ。
×

エ
\(\,\mathrm{B}\,\)の\(\,7\,\)時間未満の
累積度数は\(\,37\,\)で半数以上。
○

答え　\(\,\underline{　ア\,,\,エ　}\,\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値などの用語の意味を知っておけば問題ありません。

(6)
立方体の展開図問題です。

立体の対角線が最も長くなります。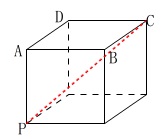答え　\(\,\underline{　ウ　}(線分\mathrm{PC})\,\)

見取り図にもどせば分かりますが
展開図のままでも構いません。

二マスで進んだ点が
反対側の頂点になるので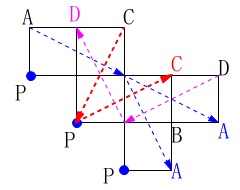二度行えば元の頂点に戻ります。

(7)
作図です。

条件
　\(\,①\,\)点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{BC}\,\)上にある。
　\(\,②\,\)\(\,\mathrm{∠BAP=30^{\circ}}\,\)である。

\(\,30°\,\)があるので正三角形を利用します。
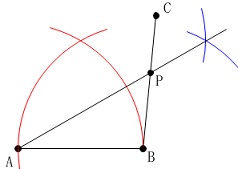\(\,1\,\)辺を\(\,\mathrm{AB}\,\)とする正三角形を書くために
\(\,\mathrm{A\,,\,B}\,\)中心に半径\(\,\mathrm{AB}\,\)の円をかきます。

２円の交点と\(\,\mathrm{B}\,\)から同じ半径の円をかいた交点と、
\(\,\mathrm{A}\,\)をつなげば\(\,60°\,\)の角の二等分線が引けます。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

作図で使う手法はそれほど多くはありません。

(8)
連続する４つの整数についての問題です。

条件
「連続する４つの整数のうち、
１つの数を除いた３つの整数の和は\(\,2021\,\)である。」

\(\,①\,\)
これは条件とは関係ありません。

連続する４つの整数は
　\(\hspace{4pt}a\,,\,a+1\,,\,a+2\,,\,a+3\)

答え　\(\underline{　a+3　}\)

\(\,②\,\)
除いた数を求めます。

連続する３つの整数の和は３の倍数になるので、
\(\,2021\,\)は\(\,3\,\)の倍数でないから
除いた数は\(\,a\,,\,a+3\,\)ではありません。

除いた整数が\(\,a+1\,\)のとき
　\(\begin{eqnarray}\displaystyle
a+(a+2)+(a+3)&=&2021\\
3a+5&=&2021\\
3a&=&2016\\
a&=&672
\end{eqnarray}\)

このとき除いた数は
　\(\hspace{10pt}a+1\\
=672+1\\
=\underline{　673　}\)

除いた数が\(\,a+2\,\)のとき
　\(\begin{eqnarray}\displaystyle
a+(a+1)+(a+3)&=&2021\\
3a+4&=&2021\\
3a&=&2017
\end{eqnarray}\)

これを満たす\(\,a\,\)は整数ではありません。

「３連続整数の和が３の倍数」を知らなくても
除いた数を\(\,a\,,\,a+3\,\)の場合も調べて行けば良いですよ。

⇒　覚えておいた方がいい倍数の見分け方

※
３連続整数の和は
　\(\hspace{10pt}n+(n+1)+(n+2)\\
=3(n+1)\)
となり\(\,3\,\)の倍数になります。

第２問文字式と不等式と確率

\(\large{\color{black}{\fbox{2}}}\)
割引のある料金の問題です。

設定が３つあるので整理しておきましょう。

通常料金
　大人　\(\,500\,\)円　子ども　\(\,200\,\)円
特別割引
　大人　\(\,500\,\)円
　子ども　\(\,200\,\)円（大人の人数分　\(\,0\,\)円）
月末割引
　大人　\(\,450\,\)円　子ども　\(\,150\,\)円

(1)
計画している日の料金についてです。

\(\,①\,\)
花子さんは
「特別割引」で「大人\(\,2\,\)人、子ども\(\,3\,\)人」
で計画しているので
　\(\hspace{10pt}500\times \color{red}{2}+200\times (3-\color{red}{2})\\
=1000+200\\
=\underline{　1200　}(円)\)

太郎さんは
「月末割引」で「大人\(\,3\,\)人、子ども\(\,5\,\)人」
で計画しているので
　\(\hspace{10pt}450\times 3+150\times 5\\
=1350+750\\
=2100　(円)\)
これが「特別割引」の日だとすると
　\(\hspace{10pt}500\times \color{red}{3}+200\times (5-\color{red}{3})\\
=1500+400\\
=1900　(円)\)
なので\(\,\underline{　200　}\,(円)\)高くなる。

\(\,②\,\)
大人\(\,x\,\)人、子ども\(\,y\,\)人（\(\,x\,＜\,y\,\)）
として「特別割引」日の料金を\(\,x\,,\,y\,\)で表します。

　\(\hspace{10pt}500\times x+200\times (y-x)\\
=500x+200y-200x\\
=\underline{　300\,x+200\,y　}(円)\)

\(\,③\,\)
「月末割引」日の料金は\(\,x\,,\,y\,\)を用いて表すと
　\(\hspace{10pt}450\,x+150\,y\)

「特別割引」と等しくなるのは
　\(\begin{eqnarray}\displaystyle
300\,x+200\,y&=&450\,x+150\,y\\
50\,y&=&150\,x\\
y&=&3\,x
\end{eqnarray}\)

つまり、
子どもの人数が大人の人数の\(\,\underline{　3　}\,\)倍のとき。

また、「月末割引」が「特別割引」より安くなるのは
　\(\begin{eqnarray}\displaystyle
300\,x+200\,y&＞&450\,x+150\,y\\
50\,y&＞&150\,x\\
y&＞&3\,x
\end{eqnarray}\)
となるときなので
「子どもが大人の\(\,3\,\)倍のとき」より
「子どもが増える\(\,\mathrm{(Y)}\,\)」か「大人が減る\(\,\mathrm{(X)}\,\)」
場合に成り立ちます。

答え　\(\,\underline{　ウ　}\,\)

※
例えば子ども\(\,10\,\)人、大人\(\,2\,\)人の場合などを
料金計算して見ると良いです。

(2)
問題は続いていますが確率を求める別問題です。

３人がスクラッチカードでくじを引き、
「少なくとも１人」はクリアファイルがプレゼントされる確率を求めます。

スクラッチカードは
　\(\,\mathrm{A\,,\,B\,,\,B}\,\)
がかくされていて
　\(\,\mathrm{\color{red}{A}}\,\)が出ればクリアファイル
　\(\,\mathrm{\color{blue}{B}}\,\)が出ればポストカード
がプレゼントされます。

樹形図で良いです。
ただし、\(\,\mathrm{B}\,\)が２つあるので区別しておきます。
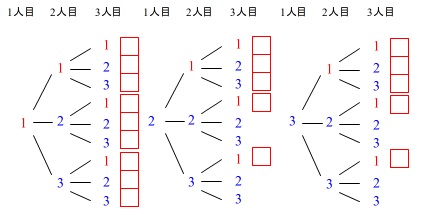\(\,\mathrm{A}\,\)を\(\,\color{red}{1}\,\)、\(\,\mathrm{B}\,\)２つを\(\,\color{blue}{2}\,,\,\color{blue}{3}\,\)とします。

答え　\(\displaystyle \underline{　\frac{19}{27}　}\)

「少なくとも」とあるので
反対の事象（余事象）
「１枚もプレゼントされない。」
確率を求めて\(\,1\,\)から引くと
　\(\hspace{10pt}\displaystyle 1-\frac{8}{27}\\
\displaystyle =\frac{19}{27}\)
でも良いです。

同じものが複数ある場合
区別すると考えやすくなりますよ。

第３問関数の問題

\(\large{\color{black}{\fbox{3}}}\)
関数\(\,y=ax^2\,(a\,＞\,0)\,\)についての問題です。

\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標はそれぞれ\(\,-1\,,\,2\,\)

各問で比例定数は違うので注意しましょう。

(1)
比例定数\(\,a\,\)の値が大きくなるとどう変化するかです。
\(\,①\,\)
「グラフの開き方」

一定の\(\,x\,\)の変化に対し\(\,y\,\)の変化が大きくなるので、
「開き方」は小さくなります。
（とがる感じになります。）

答え　\(\,\underline{　イ　}\,\)

\(\,②\,\)
「線分\(\,\mathrm{AB}\,\)の長さ」

\(\,x\,\)座標の差は一定で、
\(\,y\,\)座標の差が大きくなるので
線分\(\,\mathrm{AB}\,\)は長くなります。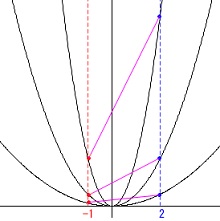
答え　\(\,\underline{　ア　}\,\)

(2)
ある条件における比例定数を求めます。

　\(\,x\,\)の変域が\(\,-1\,≦\,x\,≦\,2\,\)
のとき
　\(\,y\,\)の変域が\(\,0\,≦\,x\,≦\,2\,\)

(1)で見たグラフからも分かるように
　\(\,x=0\,\)で最小値\(\,0\,\)
　\(\,x=\color{red}{2}\,\)で最大値\(\,\color{blue}{2}\,\)
となるので
　\(\begin{eqnarray}\displaystyle
\color{blue}{2}&=&a\times (\color{red}{2})^2\\
a&=&\underline{　\frac{1}{2}　}
\end{eqnarray}\)

\(\,x=-1\,\)のときの\(\,y\,\)の値は
\(\,y\,\)の変域には関係しません。

(3)
比例定数が\(\,a=2\,\)のときです。

関数\(\hspace{4pt}y=2\,x^2\)
　\(\,\mathrm{A\,(\,-1\,,\,2\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,8\,)}\,\)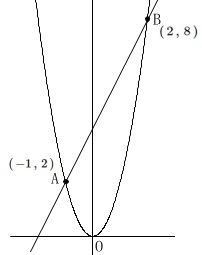①
直線\(\,\mathrm{AB}\,\)の式を求めます。

２点
　\(\,\mathrm{A\,(\,-1\,,\,2\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,8\,)}\,\)
を通る直線なので
　\(\hspace{10pt}\underline{　y=2x+4　}\)

\(\,②\,\)
２つの三角形の面積が等しくなるときの
点\(\,\mathrm{C}\,\)の\(\,x\,\)座標を求めます。

問題の通りに点\(\,\mathrm{C\,,\,D\,,\,E}\,\)があり、
　\(\,\mathrm{△BED=△ODC}\,\)
となるときの点\(\,\mathrm{C}\,\)の\(\,x\,\)座標です。\(\,①\,\)から
　\(\,\mathrm{E\,(\,0\,,\,4\,)}\,\)
は分かります。

点\(\,\mathrm{C}\,\)を文字設定しても良いですが、
等積移動を利用します。

（３）等積移動を利用する場合

２点\(\,\mathrm{O\,,\,B}\,\)を結ぶと
\(\,\mathrm{△OBD}\,\)を共通部分と見て、
　\(\,\mathrm{△OEB=△OCB}\,\)
となるとき
　\(\,\mathrm{△BED=△ODC}\,\)
となるので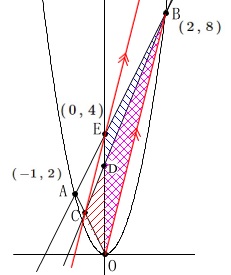直線\(\,\mathrm{OB}\,\)と直線\(\,\mathrm{CE}\,\)が平行になるときの
直線\(\,\mathrm{OA}\,\)と直線\(\,\mathrm{CE}\,\)の交点の\(\,x\,\)座標を求めれば良いのです。

分かる直線の式を先に出しておきます。
　直線\(\,\mathrm{OB}:y=4x\,\)
　直線\(\,\mathrm{OA}:y=-2x\,\)

直線\(\,\mathrm{CE}\,\)の式は
傾きが直線\(\,\mathrm{OB}\,\)と同じで\(\,4\,\)になるので
点\(\,\mathrm{E\,(\,0\,,\,4\,)}\,\)を通ることから
　直線\(\,\mathrm{CE}:y=4x+4\,\)

点\(\,\mathrm{C}\,\)は
「直線\(\,\mathrm{OA}\,\)と直線\(\,\mathrm{CE}\,\)の交点」
なので求める\(\,x\,\)座標は
　\(\begin{eqnarray}\displaystyle
-2x&=&4x+4\\
-6x&=&4\\
x&=&\underline{　-\frac{2}{3}　}
\end{eqnarray}\)

（３）文字設定する場合

この場合は共通部分を四角形\(\,\mathrm{ACDE}\,\)と見て、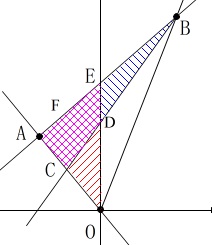　\(\,\mathrm{△ABC=△AOE}\,\)
のときに
　\(\,\mathrm{△BED=△ODC}\,\)
となります。

点\(\,\mathrm{C}\,\)の座標を
　\(\hspace{4pt}\mathrm{C}\,(\,t\,,\,-2\,t\,)\hspace{4pt}(\,t\,＜\,0)\,\)
とすると点\(\,\mathrm{C}\,\)を通り
\(\,y\,\)軸に平行な直線と直線\(\,\mathrm{AB}\,\)との交点を
　\(\,\mathrm{F}\,(\,t\,,\,2t+4\,)\)
として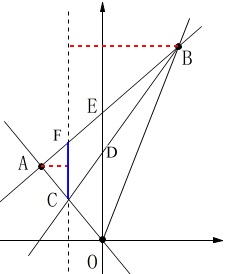底辺を\(\,\mathrm{CF}\,\)と見て
\(\,\mathrm{△ABC}\,\)の面積を\(\,t\,\)で表し
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,\{2t+4-(-2t)\}\times (3)\\
&=&6(t+1)
\end{eqnarray}\)
これが底辺\(\,\mathrm{OE}\,\)、
高さ点\(\,\mathrm{A}\,\)の\(\,x\,\)座標とみた
　\(\,\begin{eqnarray}\displaystyle
\mathrm{△AOE}&=&\frac{1}{2}\times 4\times 1\\
&=&2
\end{eqnarray}\)
と等しくなるときなので
　\(\begin{eqnarray}\displaystyle
6(t+1)&=&2\\
t+1&=&\frac{1}{3}\\
t&=&\underline{　-\frac{2}{3}　}
\end{eqnarray}\)
となります。

長さや面積は自分で出してみて下さい。

第４問図形の問題

\(\large{\color{black}{\fbox{4}}}\)
円と内接する三角形の問題です。

相似の証明、角度、線分比、面積と４題あります。

全部の問題に共通する条件は
　\(\,\mathrm{AB}\,\)は直径
　\(\,\mathrm{AB=5}\,\)
　\(\,\mathrm{AC=3}\,\)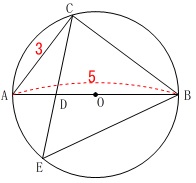他の点\(\,\mathrm{D\,,\,E}\,\)は変化します。

(1)
証明です。
　\(\,\mathrm{△ACD}\,\)∽\(\,\mathrm{△EBD}\,\)
を証明します。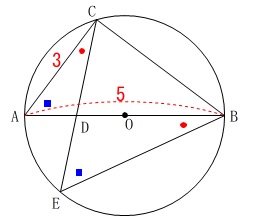円周角２つか対頂角を使えば
相似条件
「２組の角がそれぞれ等しい。」
が言えるので証明ができます。

省略します。

(2)
角度を文字を用いて表します。

条件
　\(\,\mathrm{∠BAC}=\color{red}{a^{\circ}}\,\)
　\(\,\mathrm{BC=CE}\,\)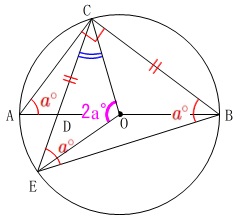1つの弧\(\,\mathrm{BC}\,\)の円周角は等しいので
　\(\,\mathrm{∠BAC=∠BEC}=\color{red}{a^{\circ}}\,\)
また\(\,\mathrm{BC=CE}\,\)から
\(\,\mathrm{△CEB}\,\)は二等辺三角形で底角は等しいので
　\(\,\mathrm{∠CEB=∠CBE}=\color{red}{a^{\circ}}\,\)
さらに中心角は円周角の\(\,2\,\)倍なので
　\(\,\mathrm{∠EOC}=\color{magenta}{2\,a^{\circ}}\,\)

半径は等しいから\(\,\mathrm{△OCE}\,\)は二等辺三角形で
底角が等しくなるから
　\(\begin{eqnarray}\displaystyle
\mathrm{∠OCD}&=&\frac{180^{\circ}-2\,a^{\circ}}{2}\\
&=&\underline{\underline{　90^{\circ}-a^{\circ}　}}
\end{eqnarray}\)

数値でも文字でも分かる角度を書き込んで行けば
ほとんどの角度は求まります。

(3)
次は長さの比です。

条件
　\(\,\mathrm{∠AOE}=\color{blue}{60^{\circ}}\,\)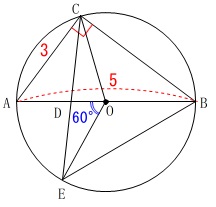このとき
線分\(\,\mathrm{DE}\,\)は線分\(\,\mathrm{AD}\,\)の何倍かを求めます。

(1)から\(\,\mathrm{△ACD}\,\)∽\(\,\mathrm{△EBD}\,\)なので
相似比を求めれば良いことになります。

ところで、
　\(\,\mathrm{∠AOE}=\color{blue}{60^{\circ}}\,\)
なので\(\,\mathrm{△OAE}\,\)は正三角形で
１辺は円の半径で\(\,\displaystyle \color{red}{\frac{5}{2}}\,\)になります。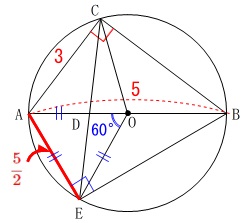
三角形\(\,\mathrm{AEB}\,\)は直角三角形なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AE^2+EB^2}&=&\mathrm{AB^2}\\
\left(\frac{5}{2}\right)^2+\mathrm{EB^2}&=&5^2\\
\frac{25}{4}+\mathrm{EB^2}&=&25\\
\mathrm{EB^2}&=&25-\frac{25}{4}\\
&=&\frac{75}{4}
\end{eqnarray}\)
\(\,\mathrm{EB}\,\)は長さだから\(\,\mathrm{EB\,＞\,0}\,\)で
　\(\hspace{10pt}\displaystyle \mathrm{EB}=\color{red}{\frac{5\sqrt{3}}{2}}\)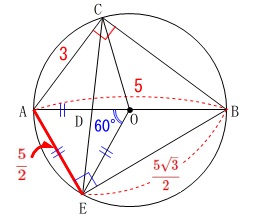これから
\(\,\mathrm{△ACD}\,\)と\(\,\mathrm{△EBD}\,\)の相似比は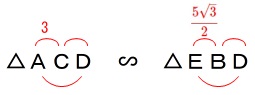
　\(\begin{eqnarray}\displaystyle
\mathrm{AC:EB}&=&3:\frac{5\sqrt{3}}{2}\\
&=&6:5\sqrt{3}
\end{eqnarray}\)

よって他の対応する辺の比も等しいから
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:ED}&=&3:\frac{5\sqrt{3}}{2}\\
3\times \mathrm{ED}&=&\frac{5\sqrt{3}}{2}\times \mathrm{AD}\\
\mathrm{ED}&=&\frac{5\sqrt{3}}{6}\times \mathrm{AD}
\end{eqnarray}\)

答え　\(\displaystyle \underline{　\frac{5\sqrt{3}}{6}　}(倍)\)

(4)
具体的な面積を求めます。

条件
　\(\,\mathrm{ＡＣ=ＣＤ}\,\)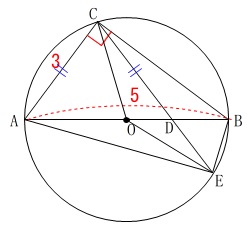このときの\(\,\mathrm{△OEB}\,\)の面積です。

\(\,\mathrm{△AEB}\,\)の半分になることは分かりますが
\(\,\mathrm{AE\,,\,BE}\,\)は分かっていません。
平行線もないので等積移動も考えにくい。
長さを具体的に求める方向で進めるかな？
ということで条件に戻ります。

　\(\,\mathrm{ＡＣ=ＣＤ}\,\)
なので\(\,\mathrm{DC=3}\,\)です。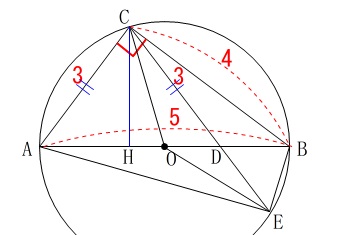部分的な長さを求めておきます。

三平方の定理から\(\,\mathrm{BC=4}\,\)で、
\(\,\mathrm{△ABC}\,\)の面積は
　\(\begin{eqnarray} \displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{AC}\\
&=&\frac{1}{2}\times 4\times 3\\
&=&\color{red}{6}
\end{eqnarray}\)

\(\,\mathrm{△ACD}\,\)（二等辺三角形）の頂点から垂線\(\,\mathrm{CH}\,\)を引くと
\(\,\mathrm{△ABC}\,\)の面積は底辺を\(\,\mathrm{AB}\,\)、
高さを\(\,\mathrm{CH}\,\)と見ることもできるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AB}\times \mathrm{CH}\\
\color{red}{6}&=&\frac{1}{2}\times 5\times \mathrm{CH}\\
\mathrm{CH}&=&\color{blue}{\frac{12}{5}}
\end{eqnarray}\)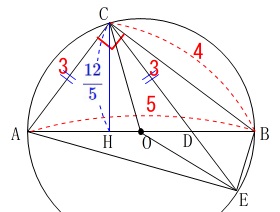
三平方の定理から
　\(\hspace{10pt}\displaystyle \mathrm{AH=HD}=\color{magenta}{\frac{9}{5}}\)
※
\(\,\mathrm{CH\,,\,AH}\,\)は
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△ACH}\,\)∽\(\,\mathrm{△CBH}\,\)
からも求まります。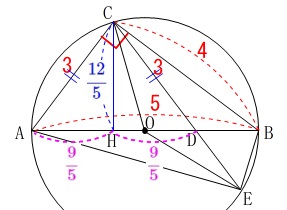このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{DB}&=&\mathrm{AB-AD}\\
&=&5-\frac{18}{5}\\
&=&\color{blue}{\frac{7}{5}}
\end{eqnarray}\)

ここからは二通りの方法で解説します。

（４）三平方の定理を利用する場合

\(\,\mathrm{△BDE}\,\)は二等辺三角形なので
　\(\hspace{10pt}\displaystyle \mathrm{\color{blue}{BE}}=\color{blue}{\frac{7}{5}}\)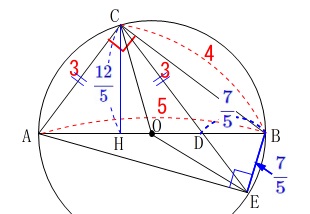三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AE^2+BE^2}&=&\mathrm{AB^2}\\
\mathrm{AE^2}+\left(\frac{7}{5}\right)^2&=&5^2\\
\mathrm{AE^2}+\frac{49}{25}&=&25
\end{eqnarray}\)
これから\(\,\mathrm{AE＞0}\,\)だから
　\(\displaystyle \mathrm{\color{red}{AE}}=\color{red}{\frac{24}{5}}\)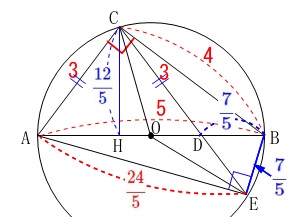
\(\,\mathrm{△OEB}\,\)の面積は\(\,\mathrm{△ABE}\,\)の半分だから
　\(\begin{eqnarray}\displaystyle
\mathrm{△OEB}&=&\frac{1}{2}\times \mathrm{△ABE}\\
&=&\frac{1}{2}\times \frac{1}{2}\times \mathrm{\color{red}{AE}}\times \mathrm{\color{blue}{BE}}\\
&=&\frac{1}{2}\times \frac{1}{2}\times \frac{24}{5}\times \frac{7}{5}\\
&=&\underline{　\frac{42}{25}　}\mathrm{cm^2}
\end{eqnarray}\)

（４）相似比を利用して面積を求める場合

　\(\,\mathrm{△ACD}\,\)∽\(\,\mathrm{△EBD}\,\)
における相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{DC:DB}&=&\color{red}{3}:\color{blue}{\frac{7}{5}}\\
&=&15:7
\end{eqnarray}\)

面積比は\(\,225:49\,\)となります。
　\(\begin{eqnarray}\displaystyle
\mathrm{△EBD}&=&\frac{49}{225}\times \mathrm{△ACD}\\
&=&\frac{49}{225}\times \frac{1}{2}\times \mathrm{AD}\times \mathrm{AE}\\
&=&\frac{49}{225}\times \frac{1}{2}\times \frac{18}{5}\times \frac{12}{5}\\
&=&\frac{49\times 12}{25\times 25}
\end{eqnarray}\)

ここで\(\displaystyle \,\mathrm{OB=\color{red}{\frac{5}{2}}}\,\)だから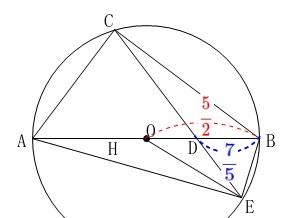
　\(\begin{eqnarray}\displaystyle
\mathrm{△OEB}&=&\frac{5}{2}\div \frac{7}{5}\times \mathrm{△EBD}\\
&=&\frac{5\times 5}{2\times 7}\times \frac{49\times 12}{25\times 25}\\
&=&\underline{　\frac{42}{25}　}\mathrm{cm^2}
\end{eqnarray}\)

相似な三角形は他にもあるので
方法はこれだけではありません。

どちらにしても、
算数の延長だと思って計算を続けるしかないです。

以上です。

⇒　奈良県公立高校入試の数学の過去問題と解答解説

後半で公立高校入試とは思えない問題が並びます。
基本が重要であることはまちがいありませんが、
基本問題だけの演習では高得点を取るのは厳しいかもしれませんね。