2022年度秋田県公立高校入試の数学第５問の問題と解説

２０２２年（令和４年）度秋田県公立高校入試の数学第５問の問題と解説です。
指定された問題を解答する平面図形の問題が２つあります。
選択ではなく受験する高校からの指定となります。
良くある基本的な問題から応用されている問題までがあるのでしっかりと条件を見ていきましょう。

2022年度秋田県公立高校入試の数学第５問の問題

第５問の問題です。

⇒　2022年度秋田県公立高校入試の数学第５問の問題

全部の問題は第１問の解説ページにありますので、
第５問の部分だけを抜いてあります。

2022年度秋田県公立高校入試の数学第５問の解説

第５問は指定された問題を解答します。
どちらも平面図形で条件を整理しやすいので
解説も簡単に進めて行きます。

Ⅰ（相似と面積比）

\(\,\large{Ⅰ}\,\)
条件は図の通りです。
　\(\,\mathrm{∠ACB}=90^{\circ}\,\)
　\(\,\mathrm{ＡＢ}\,\)⊥\(\,\mathrm{ＣＤ}\,\)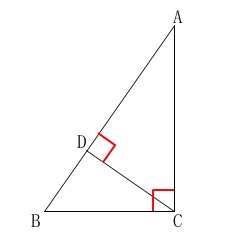直角三角形の斜辺に垂線を下ろしたよく見る形です。

（１）相似の証明

(1)は相似の証明です。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)
相似の証明をするときの第一の目標は相似条件を見つけることになります。
相似条件がそろわないと証明になりませんから。
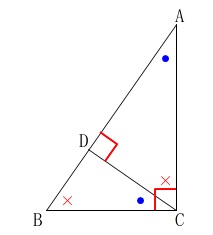三角形の内角の和は一定\(\,180°\,\)なので
垂直部分の角の他の２角の和は\(\,90°\,\)です。
\(\,\mathrm{△CDB}\,\)も相似になりますが証明するのはもっと分かり易い方です。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ACD}\,\)において
　\(\hspace{4pt}\mathrm{∠ACB=∠ADC}=90^{\circ}　（仮定）･･･①\)
　\(\hspace{4pt}\mathrm{∠BAC=∠CAD}　（共通）　･･･②\)
\(\,①②\,\)より
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)　
（証明終わり）

証明は図の中で終わらせておきましょう。

（２）円周角の定理と面積比

問題の中に埋もれて見逃しがちになりますが、
「図１の直角三角形\(\,\mathrm{ABC}\,\)」は同じ条件です。

加わる条件
　\(\,\mathrm{A\,,\,B\,,\,C\,,\,E}\,\)は円\(\,\mathrm{O}\,\)上の点。
　点\(\,\mathrm{C\,,\,D\,,\,E}\,\)は同じ直線上にある。
　\(\,\mathrm{BE}=6\,,\,\mathrm{AC}=8\,\)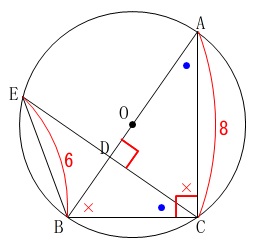点\(\,\mathrm{O}\,\)は\(\,\mathrm{AB}\,\)の中点であり、
円\(\,\mathrm{O}\,\)の中心です。
（円周角\(\,\mathrm{∠ACB=90^{\circ}}\,\)なので\(\,\mathrm{AB}\,\)が直径になります。）

①
辺の長さと角度について等しいものを聞かれているので
円周角の定理から角が等しいところや
辺が等しいと分かるところ
（すぐに見つかるところで良いです。）
に印をしておきます。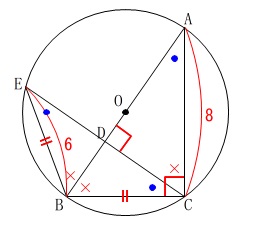具体的な長さも出せますが問題の順に進めます。

　\(\hspace{4pt}\mathrm{∠ABE=∠ACE}\)　（\(\,\color{blue}{●}\,\)の角度）
は(1)の相似と円周角の定理からいえます。

答え　\(\,\underline{　ウ　}\,\)

②
\(\,\mathrm{△BCD}\,\)と\(\,\mathrm{△ABC}\,\)の面積比を求めます。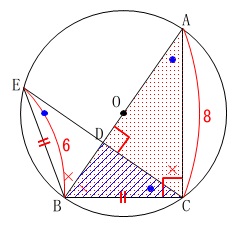『何倍か？』と『面積比は？』は同じことです。

例えば面積比\(\,a:b\,\)という比があったとして
　比\(\hspace{4pt}a:b\hspace{4pt}\)は『面積比』
　比の値\(\hspace{4pt}\displaystyle \frac{a}{b}\hspace{4pt}\)は\(\,a\,\)が\(\,b\,\)の『何倍』か
を表しています。

⇒　比例式と比の値(分数,小数,(かっこ)のついた)問題の解き方

比較する三角形は２つとも直角三角形なので
具体的に面積を求めていっても良いですね。

方法はいろいろあるのでいくつか説明しておきます。
※
時間に制限があるので、
試験中は１つの方針を立てたらそれで突き進みましょう。

１つだけ、
与えられた長さを使うことは忘れないで下さい。
ムダな条件はないのが普通です。
　　\(\,\mathrm{BE}=\color{red}{6}\,,\,\mathrm{AC}=\color{red}{8}\,\)
\(\,\mathrm{△BCE}\,\)は底角が等しくなるので二等辺三角形です。
　\(\hspace{10pt}\mathrm{BC}=\color{red}{6}\)
ついでに\(\,\mathrm{△ABC}\,\)は直角三角形なので三平方の定理から
　\(\hspace{10pt}\mathrm{AB}=\color{blue}{10}\)
となります。
　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2}&=&\mathrm{BC^2+AC^2}\\
&=&6^2+8^2\\
&=&100\\
\mathrm{AB}&=&10　(\,\mathrm{AB}\,＞\,0\,)
\end{eqnarray}\)※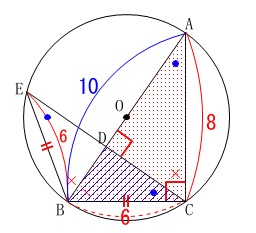
いうのを忘れていました。
単位は\(\,\mathrm{cm}\,\)ですが省略します。

先ずは簡単に答えを出しておきます。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)　∽　\(\,\mathrm{△CBD}\,\)
相似比が（斜辺を相似比とみて）
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:AC:CB}&=&10:8:6\\
&=&5:4:3
\end{eqnarray}\)
面積比は相似比の２乗になるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}:\mathrm{△ACD}:\mathrm{△CBD}&=&5^2:4^2:3^2\\
&=&25:16:9
\end{eqnarray}\)
よって、
　\(\hspace{10pt}\displaystyle \mathrm{△BCD}=\frac{9}{25}\times \mathrm{△ABC}\)
答え
　\(\hspace{10pt}\displaystyle \underline{　\frac{9}{25}　}　(倍)\)

(1)で証明した相似
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)
だけを使うなら
　相似比：\(\,5\,:\,4\,\)
　面積比：\(\,25\,:\,16\,\)
\(\,\mathrm{△BCD}\,\)は残りの\(\,\mathrm{9}\,\)となります。\(\,\mathrm{△ABC}\,\)が\(\,\color{red}{25}\,\)、\(\,\mathrm{△BCD}\,\)の面積が\(\,\color{blue}{9}\,\)となるので
　\(\hspace{10pt}\displaystyle \mathrm{△BCD}=\underline{\underline{　\frac{9}{25}　}}\times \mathrm{△ABC}\)

相似から長さを求める方向で進んだ人もいるかもしれません。
この場合も分かれるとは思いますが、
底辺の比だけ求める方法で説明していきます。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)　∽　\(\,\mathrm{△CBD}\,\)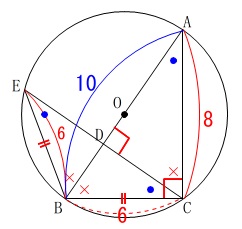(1)で証明した相似だけを利用した場合、
三平方の定理から\(\,\mathrm{AB}=\color{blue}{10}\,\)は求めているとして
　　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)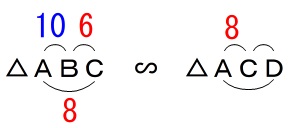比例式を立てて
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:AC}&=&\mathrm{AC:AD}\\
10:8&=&8:\mathrm{AD}\\
10\times \mathrm{AD}&=&8\times 8\\
\mathrm{AD}&=&\frac{8\times 8}{10}\\
&=&\color{magenta}{\frac{32}{5}}
\end{eqnarray}\)
残りとなる\(\,\mathrm{BD}\,\)の長さは
　\(\begin{eqnarray}\displaystyle
\mathrm{BD}&=&\mathrm{AB-AD}\\
&=&10-\frac{32}{5}\\
&=&\color{magenta}{\frac{18}{5}}
\end{eqnarray}\)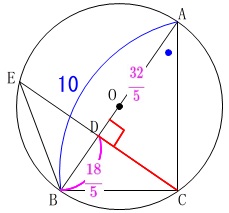\(\,\mathrm{△BCD}\,\)と\(\,\mathrm{△ABC}\,\)は高さが\(\,\mathrm{DC}\,\)で共通なので、
底辺の比が面積比となります。
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCD}&=&\frac{\mathrm{BD}}{\mathrm{AC}}\times \mathrm{△ABC}\\
&=&\color{magenta}{\frac{18}{5}}\div \color{blue}{10}\times \mathrm{△ABC}\\
&=&\frac{18}{5}\times \frac{1}{10}\times \mathrm{△ABC}\\
&=&\underline{\underline{　\frac{9}{25}　}}\times \mathrm{△ABC}
\end{eqnarray}\)

分数が出てくる比例式や倍数の求め方がわかりにくい人は
簡単な整数のとき自分でどうやって計算しているか確かめてみると良いです。
　「\(\,10\,\)は\(\,2\,\)の\(\,5\,\)倍」
　「\(\,a\,\)は\(\,b\,\)の\(\,a\div b\,\)倍」
計算方法は同じです。

⇒　比例式と比の値(分数,小数,(かっこ)のついた)問題の解き方

もちろん高さとなる\(\,\mathrm{DC}\,\)を求めて
面積を具体的にだして比較しても良いですよ。

他にも、面積の等しい合同な三角形があります。
　\(\hspace{4pt}\mathrm{△BCD}=\mathrm{△BED}\)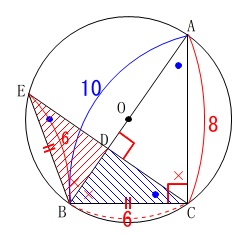\(\,\mathrm{△BED}\,\)と\(\,\mathrm{△ABC}\,\)も相似です。　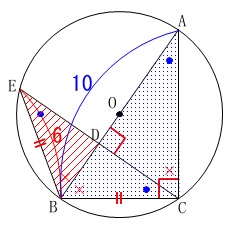相似比：\(\,\mathrm{BE:AB=6:10=3:5}\,\)
なので面積比は
　\(\hspace{4pt}\mathrm{△BED}:\mathrm{△ABC}=9:25\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCD}&=&\mathrm{△BED}\\
&=&\underline{\underline{　\frac{9}{25}　}}\times \mathrm{△ABC}
\end{eqnarray}\)

どれが早いかは別にして、どれも正解です。
自信を持って進んで下さい。

Ⅱ（相似と面積比）

\(\,\large{Ⅱ}\,\)
相似と面積比です。
円と接線が出てきますので位置関係を確認しましょう。

条件は図にある通りです。
　直線\(\,\ell\,\)は点\(\,\mathrm{B}\,\)における円\(\,\mathrm{O}\,\)の接線。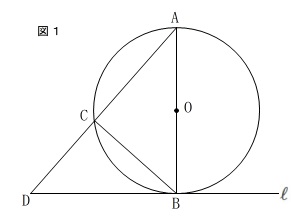

（１）相似の証明

（１）２つの三角形の相似を証明します。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ADB}\,\)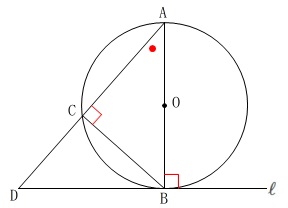これは問題\(\,\mathrm{Ⅱ}\,\)を指定された高校を受験する人なら説明は不要でしょう。
（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ADB}\,\)において
共通の角であることから
　\(\hspace{10pt}\mathrm{∠BAC}=\mathrm{∠DAB　}　･･･①\)
円の直径に対する円周角は\(\,90°\,\)なので
　\(\hspace{10pt}\mathrm{\color{red}{∠ACB}}=90^{\circ}　･･･②\)
また、円の接線と接点と中心を結ぶ半径は直行するので
　\(\hspace{10pt}\mathrm{\color{blue}{∠ABD}}=90^{\circ}　･･･③\)
②③から
　\(\hspace{10pt}\mathrm{\color{red}{∠ACB}}= \mathrm{\color{blue}{∠ABD}}　･･･④\)
①④より
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ADB}\,\)
（終わり）

相似条件をいうために
２つの条件をそろえれば良いだけです。

ところで、
この解説を順に見ている人は気がついてるかもしれませんが、
円を省いてみた条件は\(\,\large{5}\,\)の\(\,\large{\mathrm{Ⅰ}}\,\)と同じです。

ある定理（接弦定理）が背景にあるように見えますが、
定理を使えばすぐに答えが出るというわけではなく
相似や三平方の定理を組合わせた応用問題です。
しっかり手を動かして作業を続けましょう。

（２）円と接線の関係と面積比

（２）
接線と弦とのなす角の関係と
２つの面積比を求める問題が２つあります。

（１）で証明したことに条件が加わります。
　点\(\,\mathrm{E}\,\)は線分\(\,\mathrm{BC}\,\)と線分\(\,\mathrm{OD}\,\)の交点である。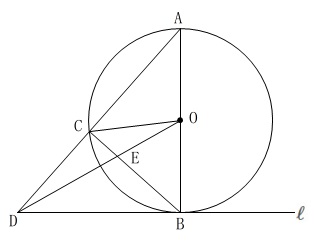
\(\,①\,\)
角度について必ずいえること（等しい角）を選びます。
問題の選択肢にある関係を順に見ていっても良いですが、
（１）で証明した相似から等しい角を同じ記号で書き込んでおきます。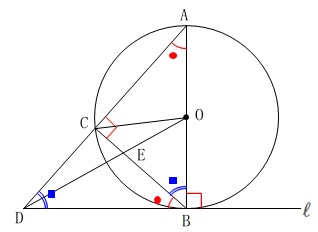ここまでは\(\,Ⅰ\,\)でも説明していますので省略します。
※
これは接弦定理という定理を証明するときの元になる関係です。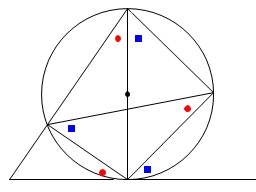接線と弦とで作られる角にある関係ですが
ここでは必要ありませんので詳しい説明は省略します。

必ずいえるのは
　\(\,\mathrm{∠BAD=∠CBD}\,\)

答え　\(\,\underline{　イ　}\,\)

選択肢を順に見ていきます。
詳しい説明はしませんので図を見ながら確認して下さい。
ア：\(\,\mathrm{∠BOE=∠OEB}\,\)
このとき\(\,\mathrm{△OBE}\,\)は二等辺三角形になりますが、
\(\,\mathrm{OB}\,\)は半径で一定なので\(\,\mathrm{D}\,\)の位置が変われば
点\(\,\mathrm{E}\,\)の位置も変わるので必ず等しいとはいえません。
ウ：\(\,\mathrm{∠ODC=∠COD}\,\)
これもアと同じことがいえます。
エ：\(\,\mathrm{∠COD=∠CBD}\,\)
これは見た目にも違いますが、
４点\(\,\mathrm{O\,,\,B\,,\,D\,,\,C}\,\)が同一円周上にあるとはいえません。

問題に『必ず』とあるときは
１つでもダメなもの（反例）があればダメですよ。

\(\,②\,\)
長さが比として条件に加わります。
　\(\hspace{4pt}\mathrm{OB:AD}=3:8\)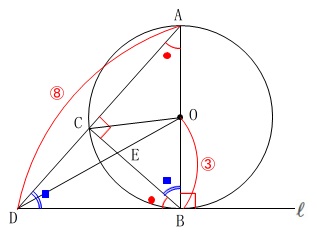問題自体に長さが与えられていないので
与えられた比は具体的な長さとしても良いですよ。

このとき\(\,\mathrm{△OBE}\,\)の面積が\(\,\mathrm{△ABD}\,\)の何倍かを求めます。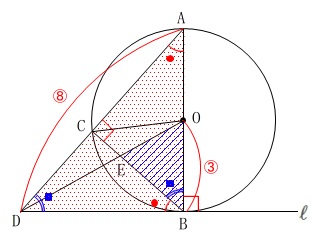方向性は線分比による圧縮になりますが、
方向はいくつか分かれると思います。
例えば、相似比を利用したい場合
　\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△ABC}\,\)の比から進める。
　\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△OBD}\,\)の比から進める。
などですが、どちらも線分比
　\(\,\mathrm{CE:EB}\,\)または\(\,\mathrm{DE:EO}\,\)
のどちらかを求める必要がありそうです。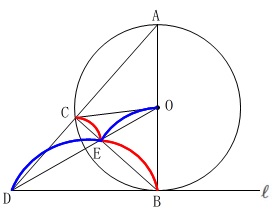または具体的な面積を求めて進めることもできます。
といっても具体的な長さはないので面積比ではありますけど。
ここでも高さをどちらにとるかは分かれますね。
　\(\,\mathrm{O}\,\)から\(\,\mathrm{BC}\,\)に下ろした垂線
　\(\,\mathrm{E}\,\)から\(\,\mathrm{OB}\,\)に下ろした垂線（遠いかな？）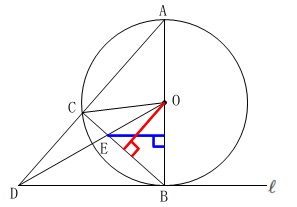
などの長さを高さと見ます。

いくつも説明すると長くなるので
ここではいろいろと復習になる方法を１つだけやっておきます。
（時間があれば自分で方針を決めて進めてみてください。）

大きな方針としては
　三平方の定理から部分的な長さを求める。
　中点連結定理と相似で線分比を求める。
　線分比を利用して面積比を求める。
となります。

高さを利用する垂線を引いたときに気がついたかもしれませんが、
半径が等しいことから\(\,\mathrm{△OBC}\,\)は二等辺三角形なので
\(\,\mathrm{O}\,\)から\(\,\mathrm{BC}\,\)に垂線を引くと\(\,\mathrm{BC}\,\)の中点におります。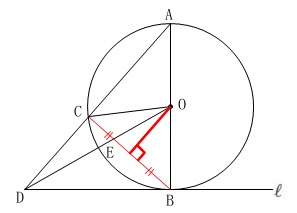そのまま\(\,\mathrm{BD}\,\)まで延長すると
線分\(\,\mathrm{BD}\,\)の中点となります。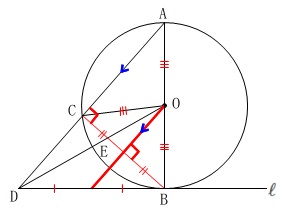中点連結定理が使えそうですね。
線分\(\,\mathrm{BD}\,\)の中点を\(\,\mathrm{G}\,\)、
\(\,\mathrm{OG}\,\)と\(\,\mathrm{BC}\,\)の交点を\(\,\mathrm{F}\,\)としておきます。
点\(\,\mathrm{F}\,\)は\(\,\mathrm{BC}\,\)の中点でもあります。

ここからは具体的な長さを求めていきます。
実際の試験だと長さを求めることが先になる部分もあると思いますが、
構いませんよ。
分かることから書き出しておく方が良いです。

できるだけ数値が整数になるよう倍数で見ても良いのですが、
ここでは与えられた比をそのままの数値として扱います。

相似と三平方の定理を利用して長さが部分的に出せます。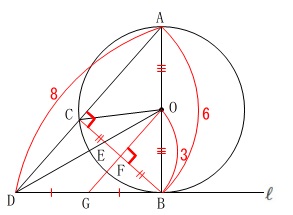三平方の定理を利用すると無理数となるので、
ここでは相似な三角形から分かる線分の長さを出します。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ADB}\,\)　∽　\(\,\mathrm{△BDC}\,\)
※
三平方の定理で進めても答えは出ますので進めてみてください。
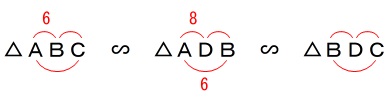ここからは比例式で求められるので自分で計算してみて下さい。
　\(\begin{eqnarray}\displaystyle
\mathrm{AB}:\mathrm{AD}&=&\mathrm{AC:AB}\\
6:8&=&\mathrm{AC}:6\\
8\times \mathrm{AC}&=&6\times 6\\
\mathrm{AC}&=&\color{blue}{\frac{9}{2}}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{DC}&=&\mathrm{AD-AC}\\
&=&8-\frac{9}{2}=\color{blue}{\frac{7}{2}}
\end{eqnarray}\)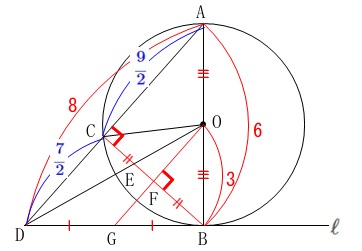中点連結定理から
　\(\hspace{10pt}\displaystyle \mathrm{OG}=\frac{1}{2}\times \mathrm{AD}=4\)
であり、
　\(\hspace{10pt}\displaystyle \mathrm{OF}=\color{magenta}{\frac{9}{4}}\hspace{4pt},\hspace{4pt}\mathrm{FG}=\color{magenta}{\frac{7}{4}}\)
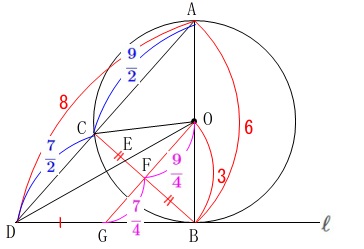使わない長さもありますが勢いで出てくる数値です。
ここで\(\,\mathrm{△EDC}\,\)∽\(\,\mathrm{△EOF}\,\)で
　相似比：\(\hspace{4pt}\displaystyle \mathrm{DC:OF}=\color{blue}{\frac{7}{2}}:\color{magenta}{\frac{9}{4}}=14:9\)
このとき相似比は同じなので
　\(\hspace{10pt}\mathrm{CE:FE}=14:9\)
　\(\hspace{10pt}\mathrm{ED:EO}=14:9\)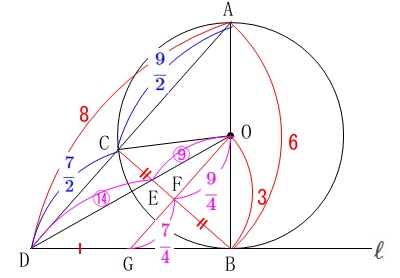ここまで来れば三角形を圧縮していきます。
どちらの三角形で考えるか分かれますがどちらでも良いです。
　\(\,\mathrm{△ABC}\,\)か\(\,\mathrm{△OBD}\,\)
好きな方を選んでください。
選んだ方で突き進めば良いです。

ここでは\(\,\mathrm{△OBD}\,\)が\(\,\mathrm{△ABD}\,\)の半分であることからはじめます。
　\(\hspace{10pt}\mathrm{AO=OB}\,\)
なので
　\(\hspace{10pt}\displaystyle \mathrm{\color{red}{△OBD}}=\color{red}{\frac{1}{2}\times \mathrm{△ABD}}\)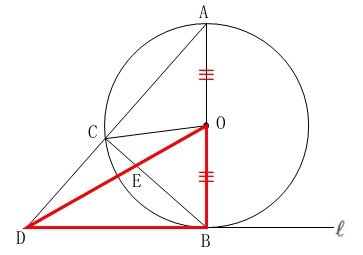次に高さを共通と見て
底辺の比が
　\(\hspace{10pt}\mathrm{ED:EO}=\color{magenta}{14}:\color{magenta}{9}\)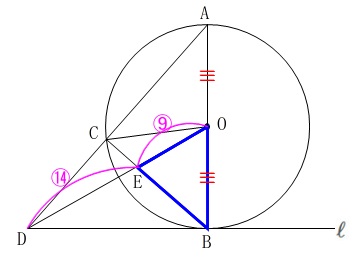なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△OBE}&=&\frac{\color{magenta}{9}}{\color{magenta}{9}+\color{magenta}{14}}\times \color{red}{\mathrm{△OBD}}\\
&=&\frac{9}{23}\times \color{red}{\frac{1}{2}\times \mathrm{△ABD}}\\
&=&\underline{\underline{　\frac{9}{46}　}}\times \mathrm{△ABD}
\end{eqnarray}\)

答え　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{9}{46}　倍}}\)

実は、ややこしい方になるのですが
私は\(\,\mathrm{△ABC}\,\)を選びました。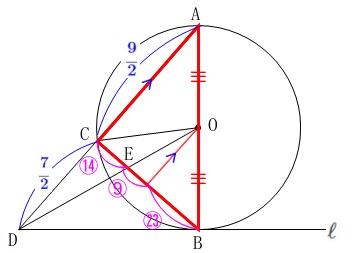\(\,\mathrm{△OBE}\,\)と\(\,\mathrm{△ABC}\,\)が先に目に飛び込んできたからです。
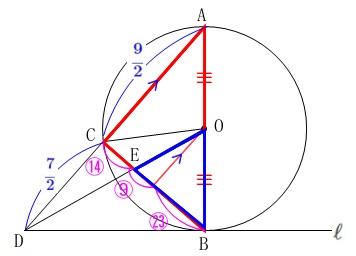こちらの圧縮の方が慣れているというのもありますが、
線分比が出せると分かった時点で突っ走っていました。
結局は\(\,\mathrm{△OBD}\,\)を選んだ方が見やすいです。
ただ、どちらを選んだとしてもそれほど時間は変わりません。線分\(\,\mathrm{BC}\,\)を抜き出して
　\(\hspace{10pt}\mathrm{CE:EF:FB}=\color{magenta}{14}:\color{magenta}{9}:\color{magenta}{23}\)
と出せるかどうかだけですね。

具体的な面積を求めて比較する方法もあります。
詳しく説明はしませんが、
間違いではありませんので構いませんよ。
（与えられた線分の長さは比なので忘れないように。）

三平方の定理から
　\(\hspace{10pt}\mathrm{BD}=\color{blue}{2\sqrt{7}}\)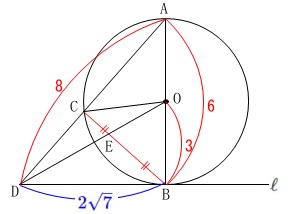
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABD}&=&\frac{1}{2}\times \mathrm{\color{blue}{BD}}\times \mathrm{\color{red}{AB}}\\
&=&\frac{1}{2}\times \color{blue}{2\sqrt{7}}\times \color{red}{6}\\
&=&6\sqrt{7}
\end{eqnarray}\)