2022年度神奈川県公立高校入試の数学の問題と解説【後半】

2022年(令和4年)度に行われた神奈川県公立高校入試の数学の問題と後半の解説です。
問１から問３までを前半として問４以降を後半としています。
問４は関数と面積比、問５は確率、問６は空間図形（立体）の問題です。
前半で割と時間をかける問題もあるのでかなり多めに感じますが、
ほぼ全分野からの出題であることは確認しておきましょう。

問６の最終問題の正答率は、
前半部分問３の最終問題よりも高かったです。
（正答率としては低めの水準ですけど。）

2022年(令和4年)度神奈川県公立高校入試の数学の問題

２０２２年（令和４年）度福神奈川県立高校入試の数学問題【後半】の\(\,\mathrm{PDF}\,\)です。

⇒　２０２２年（令和４年）度神奈川県立高校入試の数学問題【後半】

前半解説部には問題全部を載せてあります。
マークシートの注意書きがあるので確認しておきましょう。
ここでは後半の問４以降にしてあります。

2022年(令和4年)度神奈川県公立高校入試の数学【後半】の解説

早速問４の解説に入ります。

問４関数と面積比

問題の条件がややこしく見えますが、
基本的な作業で見えてくる問題です。
グラフ上で確認していきましょう。

問題とグラフに示してある通りで書く必要もありませんが、
条件をまとめておきます。
条件
　直線\(\,①\,\)：\(\,y=x+3\,\)
　曲線\(\,②\,\)：\(\,y=ax^2\,\)
　点\(\,\mathrm{A}\,\)：\(\,①\,,\,②\,\)の交点で\(\,x\,\)座標が\(\,6\,\)
　点\(\,\mathrm{B}\,\)：\(\,②\,\)上の点で\(\,\mathrm{AB}\,\)は\(\,x\,\)軸に平行
　点\(\,\mathrm{C}\,\)：\(\,①\,\)上の点で\(\,\mathrm{BC}\,\)は\(\,x\,\)軸に平行
　点\(\,\mathrm{D}\,\)：線分\(\,\mathrm{BC}\,\)と\(\,x\,\)軸との交点
　点\(\,\mathrm{E}\,\)：\(\,x\,\)軸上の点で\(\,\mathrm{DO:OE}=6:5\,\)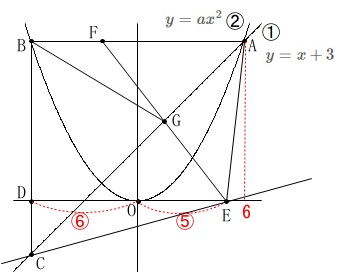直線や曲線および軸上の点であること、
また平行であることから\(\,x\,\)座標や\(\,y\,\)座標が等しい、
ということなので関数に代入して情報を書き加えます。
（代入計算は自分でやっておいて下さい。）
直線\(\,①\,\)上の点で\(\,x\,\)座標が\(\,6\,\)なので代入して
　\(\,\mathrm{A}\,\)：\(\,(\,6\,,\,9\,)\,\)
曲線\(\,②\,\)上の点で\(\,\mathrm{AB}\,\)は\(\,x\,\)軸に平行なので\(\,y\,\)座標は等しく
　\(\,\mathrm{B}\,\)：\(\,(\,-6\,,\,9\,)\,\)
直線\(\,①\,\)上の点で\(\,\mathrm{BC}\,\)は\(\,x\,\)軸に平行なので\(\,x\,\)座標は等しく
　\(\,\mathrm{C}\,\)：\(\,(\,-6\,,\,-3\,)\,\)
線分\(\,\mathrm{BC}\,\)と\(\,x\,\)軸との交点なので\(\,y=0\,\)として
　\(\,\mathrm{D}\,\)：\(\,(\,-6\,,\,0\,)\,\)
さらに\(\,\mathrm{DO:OE}=6:5\,\)なので
　\(\,\mathrm{E}\,\)：\(\,(\,5\,,\,0\,)\,\)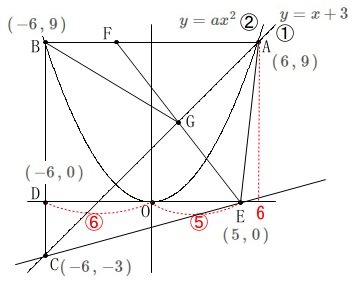ここまでは問題に関係なく条件から書き出すことですが、
ここまでができていればすんなり進みます。

(\(\,ア\,\))
曲線\(\,②\,\)の比例定数\(\,a\,\)を求めます。
曲線\(\,②\,\)は\(\,\mathrm{A\,,\,B}\,\)を通るのでどちらかを代入して
　\(\begin{eqnarray}\displaystyle
9&=&a\times (\,6\,)^2\\
a&=&\underline{\underline{　\frac{1}{4}　}}
\end{eqnarray}\)

(\(\,イ\,\))
直線\(\,\mathrm{CE}\,\)の式を\(\,y=mx+n\,\)として\(\,m\,,\,n\,\)を求めます。
　\(\,\mathrm{C}\,\)：\(\,(\,-6\,,\,-3\,)\,\)
　\(\,\mathrm{E}\,\)：\(\,(\,5\,,\,0\,)\,\)
の２点を通る直線の傾き\(\,m\,\)は
　\(\begin{eqnarray}\displaystyle
m&=&\frac{0-(-3)}{5-(-6)}\\
&=&\underline{\underline{　\frac{3}{11}　}}
\end{eqnarray}\)

傾きは変化の割合のことです。
　\(\displaystyle \color{red}{(\,変化の割合\,)=\frac{　y\,の増加量　}{　x\,の増加量　}}\)

このとき直線\(\,\mathrm{CE}\,\)の切片を\(\,\color{red}{b}\,\)とでもおきましょうか。
　\(\hspace{4pt}\displaystyle y=\frac{3}{11}\,x+\color{red}{b}\)
これが\(\,\mathrm{C\,,\,E}\,\)を通るのでどちらかを代入して
（ここでは点\(\,\mathrm{E}\,\)を代入します。）
　\(\begin{eqnarray}\displaystyle
0&=&\frac{3}{11}\times (\,5\,)+\color{red}{b}\\
\color{red}{b}&=&\underline{\underline{　-\frac{15}{11}　}}
\end{eqnarray}\)

移項のとき符号に注意が必要ですが、
グラフの位置関係と選択肢にないので気がつきますね。
点\(\,\mathrm{C}\,\)を代入して成り立つことを確認すれば確実です。
　\(\begin{eqnarray}\displaystyle
y&=&\frac{3}{11}\times (\,-6\,)-\frac{15}{11}\\
&=&\frac{-33}{11}=-3
\end{eqnarray}\)

直線の式の求め方は連立方程式でも良いです。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

ここでは連立方程式で求めれば問題２つの答えが同時に出ます。
ただし、時間を考えると私としてはおすすめしません。
※
関数問題では直線を求めることは当たり前に何度もやる作業なので、
何度も何度も連立方程式を解くというのはどうかと思うだけで、
好きにして頂いて結構ですよ。

(\(\,ウ\,\))
２つの三角形の面積比を求めます。
条件が加わりますが今までの条件は続いていますよ。
（ここに来てようやく\(\,\mathrm{F\,,\,G}\,\)の意味が分かります。）

加わる条件
　点\(\,\mathrm{F}\,\)は直線\(\,\mathrm{AB}\,\)上の点
　\(\,\mathrm{△AFE}\,\)の面積を直線\(\,①\,\)が２等分する。
　直線\(\,①\,\)と線分\(\,\mathrm{EF}\,\)との交点を\(\,\mathrm{G}\,\)とする。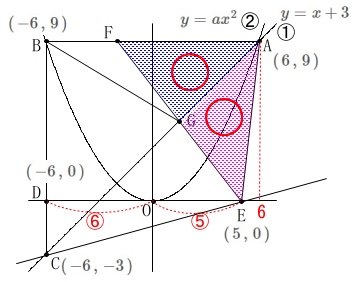このとき、
\(\,\mathrm{△BGF}\,\)と\(\,\mathrm{△CEG}\,\)の面積比を求めます。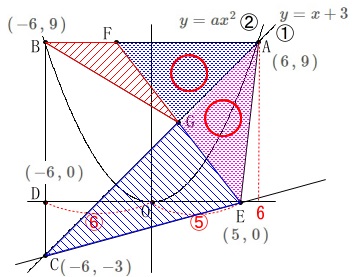グラフや図形の形を見ているといろいろな方法が考えられますが、
あれこれ考えるより２点\(\,\mathrm{F\,,\,G}\,\)の座標を求めておきましょう。
（これもいろいろあります。）

直線\(\,①\,\)が\(\,\mathrm{△AFE}\,\)を２等分するので
　\(\,\mathrm{FG=EG}\,\)
点\(\,\mathrm{G}\,\)は\(\,\mathrm{FE}\,\)の中点になります。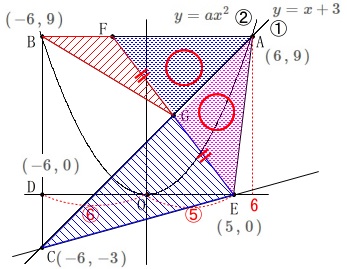文字設定した方が早いとは思いますが、
中点の座標に慣れていない人もいると思うので、
\(\,\mathrm{G}\,\)の\(\,y\,\)座標から求めるというのも方法の１つです。

⇒　三角形の面積を直線が二等分する2つのパターン

三角形を２等分する場合の考え方は確認しておいて下さい。

どちらも点の座標を求めて具体的な面積を比較するのは同じですが、
２つ説明しておきます。

（ウ）文字設定せずに求める方法

文字を使わず具体的な数値で求めていく場合、
\(\,\mathrm{G}\,\)の\(\,y\,\)座標から求めると良いです。
　\(\,\mathrm{FG=EG}\,\)
なので\(\,\mathrm{G}\,\)の\(\,y\,\)座標は\(\,\mathrm{A\,,\,B}\,\)の\(\,y\,\)座標\(\,\color{blue}{9}\,\)と、
\(\,\mathrm{D\,,\,E}\,\)の\(\,y\,\)座標\(\,\color{blue}{0}\,\)との中間になります。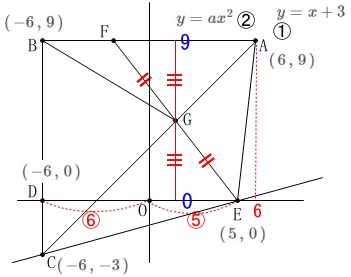このとき\(\,\mathrm{G}\,\)の\(\,y\,\)座標は
　\(\hspace{4pt}\displaystyle \frac{9+0}{2}=\frac{9}{2}\)
点\(\,\mathrm{G}\,\)は直線\(\,①\,\)上の点なので\(\,y=x+3\,\)に代入して
　\(\begin{eqnarray}\displaystyle
\frac{9}{2}&=&x+3\\
x&=&\frac{3}{2}
\end{eqnarray}\)
　\(\hspace{10pt}\displaystyle \mathrm{G}\,:\,\left(\,\frac{3}{2}\,,\,\frac{9}{2}\,\right)\)
点\(\,\mathrm{F}\,\)は\(\,x\,\)座標、\(\,y\,\)座標ともに\(\,\mathrm{E\,\rightarrow \,G}\,\)と同じ変化をするので
　\(\hspace{10pt}\displaystyle \mathrm{F}\,:\,(\,-2\,,\,9\,)\)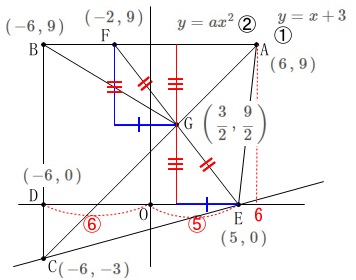となります。

また、直線\(\,①\,\)と\(\,x\,\)軸との交点\(\,\mathrm{K}\,\)は
\(\,y=x+3\,\)において\(\,y=0\,\)とすることで
　\(\hspace{4pt}\mathrm{K}\,:\,(\,-3\,,\,0\,)\)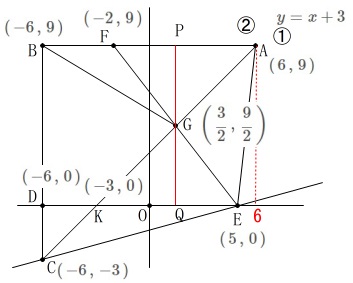ここまで点の座標が出れば三角形の面積が具体的に求めることができます。
（\(\,\mathrm{G}\,\)を通り\(\,y\,\)軸に平行な直線と\(\,\mathrm{AB\,,\,DE}\,\)との交点を\(\,\mathrm{P\,,\,Q}\,\)としています。）
　\(\begin{eqnarray}\displaystyle
\mathrm{△BGF}&=&\frac{1}{2}\times \mathrm{BF}\times \mathrm{PG}\\
&=&\frac{1}{2}\times 4\times \left(\,9-\frac{9}{2}\,\right)\\
&=&\frac{1}{2}\times 4\times \frac{9}{2}\\
&=&9
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{△CEG}&=&\mathrm{△CKE+△GKE}\\
&=&\frac{1}{2}\times \mathrm{KE}\times \mathrm{DC}+\frac{1}{2}\times \mathrm{KE}\times \mathrm{GQ}\\
&=&\frac{1}{2}\times \mathrm{KE}\times \mathrm{DC+GQ}\\
&=&\frac{1}{2}\times 8\times \left\{\frac{9}{2}-(-3)\,\right\}\\
&=&\frac{1}{2}\times 8\times \frac{15}{2}\\
&=&30
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△BGF:△CEG}&=&9:30\\
&=&\underline{　3:10　}
\end{eqnarray}\)　

簡単に言ってしまえば、
条件を満たすときのそれぞれの点を求めてしまえば良いということです。

（ウ）文字設定して点の座標を求める方法

条件を満たす場合の点\(\,\mathrm{F}\,\)の座標が知りたいので
点\(\,\mathrm{F}\,\)を\(\,\color{blue}{(\,t\,,\,9\,)}\,\)とします。
直線\(\,①\,\)と\(\,x\,\)軸との交点を\(\,\mathrm{K}\,\)とするのは先ほどと同じです。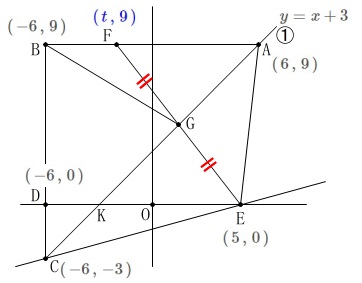（点\(\,\mathrm{F}\,\)の\(\,y\,\)座標は点\(\,\mathrm{A\,,\,B}\,\)の\(\,y\,\)座標と同じ。）

点\(\,\mathrm{G}\,\)は\(\,\mathrm{FE}\,\)の中点で、
　\(\hspace{4pt}\displaystyle \left(\,\frac{t+5}{2}\,,\,\frac{9+0}{2}\,\right)=\color{red}{\left(\,\frac{t+5}{2}\,,\,\frac{9}{2}\,\right)}\)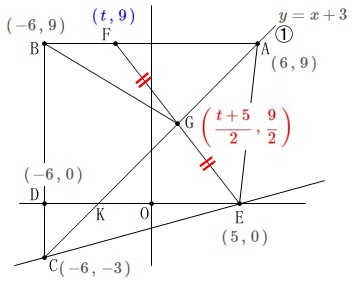これが直線\(\,①\,\)上の点なので\(\,y=x+3\,\)に代入して
　\(\begin{eqnarray}\displaystyle
\frac{9}{2}&=&\frac{t+5}{2}+3\\
9&=&t+5+6\\
t&=&-2
\end{eqnarray}\)
よって、
　\(\hspace{4pt}\mathrm{F}：(\,-2\,,\,9\,)\,\)
このとき
　\(\hspace{4pt}\displaystyle \mathrm{G}：\left(\,\frac{3}{2}\,,\,\frac{9}{2}\,\right)\,\)ここからは文字設定しない場合と同じです。

条件を定めると部分的な面積は固定されるので
他にも方法はありますので自分で試して見て下さい。
時間が足りなくなるくらいの量だと思うので突っ走った方が良いです。

図形だけを見ていると\(\,\mathrm{B\,,\,C}\,\)を通る\(\,\mathrm{FE}\,\)に平行な直線を引きたくなりますが、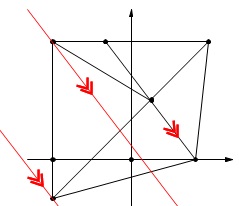やめておきます。
素直に点の座標を求めに行きましょう。

問５確率と図形と文字式の融合

さいころ２つの確率なので樹形図で良いですが、
その前に線分比と正方形の面積比較があります。

条件
　線分\(\,\mathrm{PQ}\,\)の長さは\(\,10\,\)
　大きいさいころの出た目を\(\,\color{red}{a}\,\)
　小さいさいころの出た目を\(\,\color{blue}{b}\,\)
　\(\,\mathrm{PR:RQ}=\color{red}{a}:\color{blue}{b}\,\)
　\(\,\mathrm{PR}\,\)を１辺とする正方形が\(\,\mathrm{X}\,\)
　\(\,\mathrm{RQ}\,\)を１辺とする正方形が\(\,\mathrm{Y}\,\)※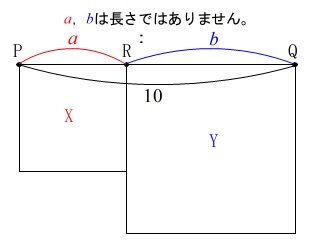
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。

さいころは同時に１回投げます。
問題に「例」があるので、
同じようにいくつか調べてみると良いです。
（分数が出てくるのでメンドウであることが分かるでしょう。）

(\(\,ア\,\))
\(\,\mathrm{X}\,\)の面積と\(\,\mathrm{Y}\,\)の面積が等しくなる確率です。

２つの正方形の１辺が等しくなるときなので
　\(\hspace{4pt}\color{red}{a}=\color{blue}{b}\)
つまり２つのさいころの出た目が同じときの確率ですね。
　\(\hspace{10pt}\displaystyle \frac{6}{36}=\underline{\underline{　\frac{1}{6}　}}\)

(\(\,イ\,\))
\(\,\mathrm{X}\,\)の面積が\(\,\mathrm{Y}\,\)の面積より\(\,25\,\)以上大きくなるときの確率です。

\(\,\mathrm{X}\,\)の面積の方が大きいので\(\,\color{red}{a}≦\color{blue}{b}\,\)のときは条件を満たしません。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\,\color{red}{1}\, & × & × & × & × & × & × \\ \hline
\color{red}{2} & & × & × & × & × & × \\ \hline
\color{red}{3} & & & × & × & × & × \\ \hline
\color{red}{4} & & & & × & × & × \\ \hline
\color{red}{5} & & & & & × & × \\ \hline
\color{red}{6} & & & & & & × \\ \hline
\end{array}\)
いくらか絞れましたが残り\(\,15\,\)通りの中には分数も出てきます。
全てを調べるにしても結構大変でしょう。

方法は２つあります。
文字式で処理するか、根性？で全て調べるかです。笑

調べるにしても差が\(\,25\,\)以上になれば良いので
差が小さい方から調べれば少しは楽になりますよ。

（イ）文字式で処理する場合

文字が２つあるのでややこしく感じますが、
関係式を出して条件を満たすときを調べます。

\(\,\mathrm{X}\,\)の１辺と\(\,\mathrm{Y}\,\)の１辺を\(\,a\,,\,b\,\)で表すと
線分\(\,10\,\)を\(\,a:b\,\)に分けるので
\(\,\mathrm{X}\,\)の１辺は
　\(\hspace{4pt}\displaystyle \frac{a}{a+b}\times 10=\color{red}{\frac{10\,a}{a+b}}\)
\(\,\mathrm{Y}\,\)の１辺は
　\(\hspace{4pt}\displaystyle \frac{b}{a+b}\times 10=\color{blue}{\frac{10\,b}{a+b}}\)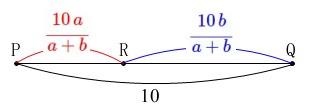長さの和が\(\,10\,\)になっていることを確認しておきましょう。

正方形の面積の差が\(\,25\,\)以上なので
　\(\hspace{4pt}\displaystyle \left(\,\frac{10\,a}{a+b}\right)^2-\left(\,\frac{10\,b}{a+b}\right)^2≧25\)
これを少し見やすく変形します。
　\(\begin{eqnarray}\displaystyle
\left(\,\frac{10\,a}{a+b}\right)^2-\left(\,\frac{10\,b}{a+b}\right)^2&≧&25\\
\frac{100\,a^2}{(\,a+b\,)^2}-\frac{100\,b^2}{(\,a+b\,)^2}&≧&25\\
100\,a^2-100\,b^2&≧&25(\,a+b\,)^2\\
100(\,a^2-b^2\,)^2&≧&25(\,a+b\,)^2\\
4(\,a^2-b^2\,)^2&≧&(\,a+b\,)^2\\
4(\,a+b\,)(\,a-b\,)&≧&(\,a+b\,)^2\\
4(\,a-b\,)&≧&a+b
\end{eqnarray}\)
\(\,a+b＞0\,\)なので両辺を割っても不等号の向きは変わりません。
※
この変形はややこしいですが自分でやってみて下さい。
分数を含んでいますが因数分解と不等号の性質を両方確認できます。

さらに、
　\(\begin{eqnarray}\displaystyle
4(\,a-b\,)&=&a+b\\
4a-4b&≧&a+b\\
3\,a&≧&5\,b\\
a&≧&\frac{5}{3}\,b　･･･①
\end{eqnarray}\)

\(\,a\,＞\,b\,\)のときを見れば良いので\(\,a\,＞\,2\,\)を調べます。
　\(\hspace{4pt}a=2\,\)のとき\(\,b=1\,\)
　\(\hspace{4pt}a=3\,\)のとき\(\,b=1\,\)
（\(\,b=2\,\)のとき\(\,①\,\)を満たしていません。）
　\(\hspace{4pt}a=4\,\)のとき\(\,b=1\,,\,2\,\)
（\(\,b=3\,\)のとき\(\,①\,\)を満たしていません。）
　\(\hspace{4pt}a=5\,\)のとき\(\,b=1\,,\,2\,,3\,\)
（\(\,b=4\,\)のとき\(\,①\,\)を満たしていません。）
　\(\hspace{4pt}a=6\,\)のとき\(\,b=1\,,\,2\,,\,3\)
（\(\,b=4\,,\,5\,\)のとき\(\,①\,\)を満たしていません。）
この問題はこの「調べる」という作業を
するか、しないかで答えが出せるかどうかの問題です。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\,\color{red}{1}\, & × & × & × & × & × & × \\ \hline
\color{red}{2} & ○ & × & × & × & × & × \\ \hline
\color{red}{3} & ○ & × & × & × & × & × \\ \hline
\color{red}{4} & ○ & ○ & × & × & × & × \\ \hline
\color{red}{5} & ○ & ○ & ○ & × & × & × \\ \hline
\color{red}{6} & ○ & ○ & ○ & × & × & × \\ \hline
\end{array}\)
答え
　\(\hspace{10pt}\displaystyle \frac{10}{36}=\underline{\underline{　\frac{5}{18}　}}\)

これをややこしい文字式処理をせずに求める方法が次です。

（イ）樹形図か表を利用して実計算で調べる場合

文字式で求めたときの説明をもう一度しておきます。

面積の差が\(\,25\,\)以上のときなので
　\(\hspace{10pt}\color{red}{a}\,＞\,\color{blue}{b}\)
のときだけです。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\,\color{red}{1}\, & × & × & × & × & × & × \\ \hline
\color{red}{2} & \color{red}{\leftarrow} & × & × & × & × & × \\ \hline
\color{red}{3} & & \color{red}{\leftarrow} & × & × & × & × \\ \hline
\color{red}{4} & & & \color{red}{\leftarrow} & × & × & × \\ \hline
\color{red}{5} & & & & \color{red}{\leftarrow} & × & × \\ \hline
\color{red}{6} & & & & & \color{red}{\leftarrow} & × \\ \hline
\end{array}\)
これを表で確認していきます。
（樹形図でも良いですよ。）

全て調べるのは数が割と多いので、
上の表の矢印方向に調べて行きます。

条件を満たしたところより左は条件を必ず満たすので
（面積の差はより大きくなる。）
調べる必要がなくなるからです。

ここでは\(\,\mathrm{X}\,\)の面積を\(\,V_1\,\)、\(\,\mathrm{Y}\,\)の面積を\(\,V_2\,\)としておきます。
・\(\,a=2\,,\,b=1\)のとき（\(\,10\,\)を\(\,2：1\,\)に分けるので）
\(\,\mathrm{X}\,\)の１辺は\(\displaystyle \,\frac{20}{3}\,\)、\(\,\mathrm{Y}\,\)の１辺は\(\displaystyle \,\frac{10}{3}\,\)となるから
　\(\begin{eqnarray}\displaystyle
V_1-V_2&=&\left(\,\frac{20}{3}\,\right)^2-\left(\,\frac{10}{3}\,\right)^2\\
&=&\frac{400-100}{9}\\
&=&\frac{300}{9}=\frac{100}{3}=33.\cdots　Ok!
\end{eqnarray}\)
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\,\color{red}{1}\, & × & × & × & × & × & × \\ \hline
\color{red}{2} & \color{red}{○} & × & × & × & × & × \\ \hline
\color{red}{3} & & \color{red}{\leftarrow} & × & × & × & × \\ \hline
\color{red}{4} & & & \color{red}{\leftarrow} & × & × & × \\ \hline
\color{red}{5} & & & & \color{red}{\leftarrow} & × & × \\ \hline
\color{red}{6} & & & & & \color{red}{\leftarrow} & × \\ \hline
\end{array}\)
　
・\(\,a=3\,,\,b=2\)のとき（\(\,10\,\)を\(\,3：2\,\)に分けるので）
\(\,\mathrm{X}\,\)の１辺は\(\,6\,\)、\(\,\mathrm{Y}\,\)の１辺は\(\,4\,\)となるから
　\(\begin{eqnarray}\displaystyle
V_1-V_2&=&6^2-4^2\\
&=&36-16\\
&=&20　×
\end{eqnarray}\)
・\(\,a=3\,,\,b=1\)のとき（\(\,10\,\)を\(\,3：1\,\)に分けるので）　
\(\,\mathrm{X}\,\)の１辺は\(\displaystyle \,\frac{30}{4}\,\)、\(\,\mathrm{Y}\,\)の１辺は\(\displaystyle \,\frac{10}{4}\,\)となるから
　\(\begin{eqnarray}\displaystyle
V_1-V_2&=&\left(\,\frac{30}{4}\,\right)^2-\left(\,\frac{10}{4}\,\right)^2\\
&=&\frac{900-100}{16}\\
&=&\frac{800}{16}=50　Ok!
\end{eqnarray}\)
（正方形の１辺は約分した数で面積計算してももちろん良いですよ。）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\,\color{red}{1}\, & × & × & × & × & × & × \\ \hline
\color{red}{2} & \color{red}{○} & × & × & × & × & × \\ \hline
\color{red}{3} & \color{red}{○} & \color{red}{×} & × & × & × & × \\ \hline
\color{red}{4} & & & \color{red}{\leftarrow} & × & × & × \\ \hline
\color{red}{5} & & & & \color{red}{\leftarrow} & × & × \\ \hline
\color{red}{6} & & & & & \color{red}{\leftarrow} & × \\ \hline
\end{array}\)
これを続けていきます。
　
・\(\,a=4\,\)のとき\(\,b=3\,\)は\(\,×\,\)、\(\,b=2\,\)は\(\,Ok!\,\)
ここで\(\,b=1\,\)も\(\,Ok!\,\)となります。
・\(\,a=5\,\)のとき\(\,b=4\,\)は\(\,×\,\)、\(\,b=3\,\)は\(\,Ok!\,\)
ここで\(\,b=1\,,\,2\,\)も\(\,Ok!\,\)となります。
・\(\,a=6\,\)のとき\(\,b=5\,,\,4\,\)は\(\,×\,\)、\(\,b=3\,\)は\(\,Ok!\,\)
ここで\(\,b=1\,,\,2\,\)も\(\,Ok!\,\)となります。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\,\color{red}{1}\, & × & × & × & × & × & × \\ \hline
\color{red}{2} & \color{red}{○} & × & × & × & × & × \\ \hline
\color{red}{3} & \color{red}{○} & \color{red}{×} & × & × & × & × \\ \hline
\color{red}{4} & \color{red}{○} & \color{red}{○} & \color{red}{×} & × & × & × \\ \hline
\color{red}{5} & \color{red}{○} & \color{red}{○} & \color{red}{○} & \color{red}{×} & × & × \\ \hline
\color{red}{6} & \color{red}{○} & \color{red}{○} & \color{red}{○} & \color{red}{×} & \color{red}{×} & × \\ \hline
\end{array}\)

答え\(\hspace{10pt}\displaystyle \frac{10}{36}=\underline{\underline{　\frac{5}{18}　}}\)
ここで面積計算は\(\,10\,\)回していることになります。

文字式で処理できないと感じて、
時間に余裕があれば根性で地道に計算しまくりましょう。

問６空間図形

空間図形の問題ですが、
立体（四角柱）があるだけで平面図形の問題です。
（当会の会員にはおなじみですね。）

四角柱の条件
　\(\,\mathrm{AB=5\,,\,BC=1\,,\,AD=4}\,\)
　底面\(\,\mathrm{ABCD}\,\)は\(\,\mathrm{∠ADC=∠BCD=90°}\,\)の台形
　高さは\(\,\mathrm{AB=BF=CG=DH=1}\,\)※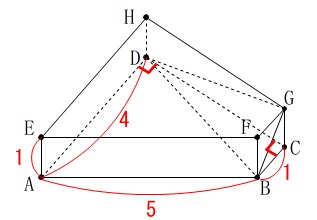
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。

(\(\,ア\,\))
四角柱の体積を求めます。

底面が台形、高さが\(\,1\,\)の四角柱なので
底面の面積を求めに行きましょう。

高さとなる\(\,\mathrm{DC}\,\)の長さが欲しいので
点\(\,\mathrm{B}\,\)から\(\,\mathrm{AD}\,\)に垂線を下ろし交点を\(\,\mathrm{K}\,\)とします。
このとき\(\,\mathrm{DC}\,\)と\(\,\mathrm{BK}\,\)の長さは同じです。（長方形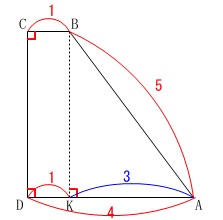）よく出てくる比なのですぐに求まるとは思いますが、
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AK^2+BK^2}&=&\mathrm{AB^2}\\
\mathrm{BK^2}&=&\mathrm{AB^2-AK^2}\\
&=&5^2-3^2\\
&=&16\\
\mathrm{BK}&=&\pm 4
\end{eqnarray}\)
\(\,\mathrm{BK}\,\)は長さなので\(\,\mathrm{BK\,＞\,0}\,\)だから
　\(\hspace{10pt}\mathrm{BK}=\mathrm{DC}=\color{magenta}{4}\)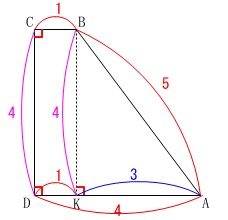よって、
台形\(\,\mathrm{ABCD}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{\color{red}{1}+\color{red}{4}}{2}\times \color{magenta}{4}\\
&=&10
\end{eqnarray}\)
四角柱の高さは\(\,1\,\)なので求まる体積\(\,V\,\)は
　\(\hspace{10pt}V=\underline{　10　}(\,\mathrm{cm^3}\,)\)

基本段階の人もここまではなんとか出しておきたいですね。

(\(\,\mathrm{イ}\,\))
三角形の面積を求めます。
\(\,\mathrm{△BDG}\,\)を抜き出しましょう。

三平方の定理を使いますが計算は省略するので
自分でやって確認しておいてください。

人の解答見てできる気になってはダメですよ。

(\(\,ア\,\))で求めた長さを書き込みします。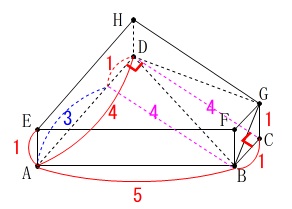\(\,\mathrm{△BDG}\,\)を作る3辺を含む面を部分的に抜き出しましょう。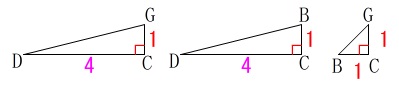これから
　\(\hspace{10pt}\mathrm{DG}=\color{blue}{\sqrt{17}}\)
　\(\hspace{10pt}\mathrm{BD}=\color{blue}{\sqrt{17}}\)
　\(\hspace{10pt}\mathrm{BG}=\color{red}{\sqrt{2}}\)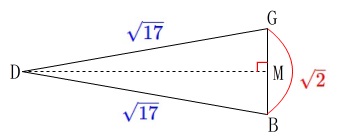二等辺三角形になるので、
頂点\(\,\mathrm{D}\,\)から\(\,\mathrm{BC}\,\)に垂線を引いて交点を\(\,\mathrm{M}\,\)としています。
点\(\,\mathrm{M}\,\)は\(\,\mathrm{BG}\,\)の中点になるので高さ\(\,\mathrm{DM}\,\)は
三平方の定理から
（ここは計算も書いておきます。）
　\(\begin{eqnarray}
\mathrm{DM^2}&=&\mathrm{DG^2-GM^2}\\
&=&(\sqrt{17})^2-\left(\,\frac{\sqrt{2}}{2}\,\right)^2\\
&=&17-\frac{1}{2}\\
&=&\frac{33}{2}
\end{eqnarray}\)
\(\,\mathrm{DM\,＞\,0}\,\)なので（長さです。）
　\(\hspace{10pt}\displaystyle \mathrm{DM}=\color{magenta}{\frac{\sqrt{33}}{\sqrt{2}}}\)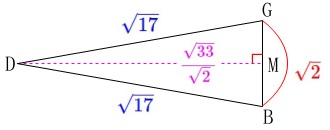よって、
　\(\begin{eqnarray}
\mathrm{△BDG}&=&\frac{1}{2}\times \color{red}{\sqrt{2}}\times \color{magenta}{\frac{\sqrt{33}}{\sqrt{2}}}\\
&=&\underline{\underline{　\frac{\sqrt{33}}{2}　}}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

分母の有理化は途中段階でしても良いですよ。
場合によりますが、
後で約分できることに期待してやらないだけです。笑

(\(\,ウ\,\))
線分の長さの和を求めますが、
「最も短くなる」
とあるので会員は方針が立てやすかったでしょう。

ただ、神奈川県では例年ここにあるんですよ。
やたらハードな計算が、です。
まあ、
計算が割とハードでも内容自体は基本の組み合わせなので、
地道にとっとと計算していけば良いだけです。

分かる人は分かる、
分からない人は分からない問題なので簡単に済ませます。

条件
　点\(\,\mathrm{I}\,\)は辺\(\,\mathrm{ＣＤ}\,\)上の点
　\(\,\mathrm{CI:ID=7:3}\,\)
　点\(\,\mathrm{A}\,\)と点\(\,\mathrm{I}\,\)を結んで最も短くなる。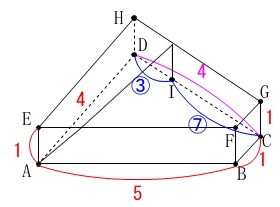折れ線が「最も短くなる」のは一直線になったときなので、
展開図で考えます。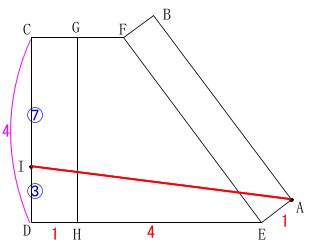三平方の定理を利用するんだな、
と思えるので直角三角形を作りましょう。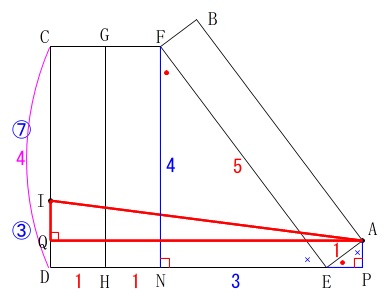最終的には\(\,\mathrm{△AIQ}\,\)で三平方の定理ですが、
それまでにいくつか線分の長さを出さなければなりません。

先ずは\(\,\mathrm{CI:ID=7:3}\,\)から
　\(\hspace{10pt}\displaystyle \mathrm{IC}=\frac{7}{7+3}\times 4=\color{blue}{\frac{14}{5}}\)
　\(\hspace{10pt}\displaystyle \mathrm{ID}=\frac{3}{7+3}\times 4=\color{blue}{\frac{6}{5}}\)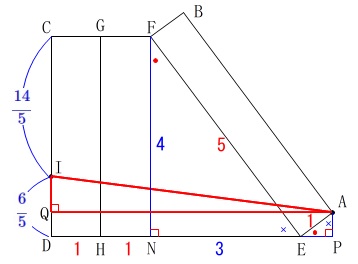また、
　\(\,\mathrm{△FNE}\,\)　∽　\(\,\mathrm{△EPA}\,\)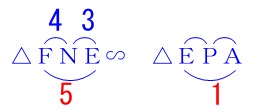となるので
　\(\hspace{10pt}\displaystyle \mathrm{AP}=\color{red}{\frac{3}{5}}\,,\,\hspace{10pt}\displaystyle \mathrm{PE}=\color{red}{\frac{4}{5}}\)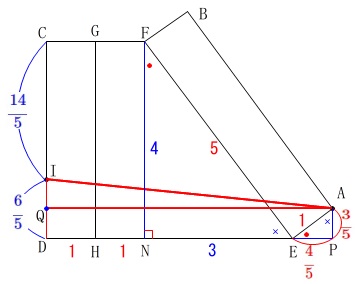このとき\(\,\mathrm{APDQ}\,\)は長方形だから\(\,\mathrm{DQ}\,\)も\(\,\mathrm{AP}\,\)と同じなので
　\(\hspace{10pt}\displaystyle \mathrm{DQ}=\color{red}{\frac{3}{5}}\)
ここで点\(\,\mathrm{Q}\,\)は\(\,\mathrm{ID}\,\)の中点になっていることが分かります。
（利用するかどうかは別にして。）
　\(\begin{eqnarray}
\mathrm{IQ}&=&\mathrm{ID-DQ}\\
&=&\color{blue}{\frac{6}{5}}-\color{red}{\frac{3}{5}}\\
&=&\color{red}{\frac{3}{5}}
\end{eqnarray}\)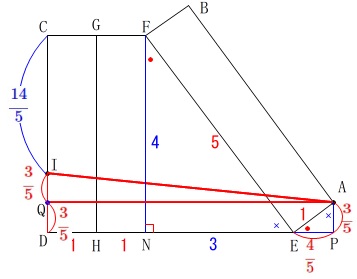\(\,\mathrm{△AIQ}\,\)において三平方の定理から
　\(\begin{eqnarray}
\mathrm{AI^2}&=&\mathrm{IQ^2+AQ^2}\\
&=&\left(\,\frac{3}{5}\,\right)^2+\left(\,1+1+3+\frac{4}{5}\,\right)^2\\
&=&\left(\,\frac{3}{5}\,\right)^2+\left(\,\frac{29}{5}\,\right)^2\\
&=&\frac{9}{25}+\frac{841}{25}\\
&=&\frac{850}{25}\\
&=&34\\
\mathrm{AI}&=&\sqrt{34}　(\,\mathrm{AI}\,＞\,0\,)
\end{eqnarray}\)