2022年(令和4年)度神奈川県公立高校入試の数学の問題と解説

2022年(令和4年)度に行われた神奈川県公立高校入試の数学の問題と解説です。
マークシート部分が割と多いですがカンでは埋まりません。
記述式と同じように基本をおさえしっかり作業していきましょう。
軽めですが計算力を試す問題もしっかりあり、
問題数は普通ですが受験生にはかなり多く感じたでしょう。

平均点は１００点満点で\(\,52.9\,\)です。

2022年(令和4年)度神奈川県公立高校入試の数学の問題

２０２２年（令和４年）度福神奈川県立高校入試の数学問題\(\,\mathrm{PDF}\,\)です。

⇒　２０２２年（令和４年）度神奈川県立高校入試の数学問題

マークシートや仕方や答えの書き方の注意書きがあるので、
最初のページから載せています。

2022年(令和4年)度神奈川県公立高校入試の数学の解説

マークシート部分（記号を選ぶ問題）が多くありますが
受験生にとって時間に余裕がある問題量とはいえません。
基本から標準応用まで差がつきやすい問題となっています。

問題は問１から問６まであります。

手強く感じる問題もあるかもしれませんが、
ミスに気をつけて基本通りにささっと進めましょう。

今度こそは簡単に済ませる予定です。
※
答えは導きますが記入番号は自分で確認してください。

問１計算小問集合

計算と展開の問題が５つあります。
(\(\,ア\,\))
　\(\hspace{10pt}-6+(-9)\\
=-6-9\\
=\underline{　-15　}\)
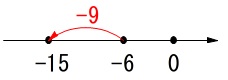マイナス（\(\,－\,\)）の数を足すのは数直線で左に移動するということです。

(\(\,イ\,\))
　\(\hspace{10pt}\displaystyle -\frac{3}{8}+\frac{2}{3}\\
\displaystyle =\frac{-3\times 3+2\times 8}{24}\\
\displaystyle =\frac{-9+16}{24}\\
\displaystyle =\underline{\underline{　\frac{7}{24}　}}\)

分数計算は通分して分子の計算に集中すると
早いしミスも少なくなります。

(\(\,ウ\,\))
　\(\hspace{10pt}\displaystyle \frac{3x-y}{4}-\frac{x-2y}{6}\\
\displaystyle =\frac{3(3x-y)-2(x-2y)}{12}\\
\displaystyle =\frac{9x-3y-2x+4y}{12}\\
\displaystyle =\underline{\underline{　\frac{7x+y}{12}　}}\)

文字式でも分数計算は同じです。
２行目から３行目の分子の展開は符号注意です。

(\(\,エ\,\))
　\(\hspace{10pt}\displaystyle \frac{18}{\sqrt{2}}-\sqrt{32}\\
\displaystyle =\frac{18\sqrt{2}}{2}-4\sqrt{2}\\
\displaystyle =9\sqrt{2}-4\sqrt{2}\\
=\underline{　5\sqrt{2}　}\)

分母の有理化やルートの中の簡素化など、
無理数の処理の仕方は人によって段階があります。
この問題は暗算でもできる計算ですがていねいに処理しましょう。
特に素因数分解は確実にやっておきましょう。

(\(\,オ\,\))
　\(\hspace{10pt}(x-2)(x-5)-(x-3)^2\\
=(x^2-7x+10)-(x^2-6x+9)\\
=x^2-7x+10-x^2+6x-9\\
=\underline{　-x+1　}\)

ミスが起こりやすいのは、
（かっこ）を外す２行目から３行目です。
暗算できる程度の計算ほどていねいに進めましょう。

問１は以上です。

問２方程式や関数などの小問集合

問２は方程式や関数の基本、代入問題など５問あります。

(\(\,ア\,\))
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 0.2\,x+0.8\,y=1　･･･①\\
\hspace{4pt}\displaystyle \frac{1}{2}\,x+\frac{7}{8}\,y=-2　･･･②
\end{cases}\)

小数や分数の係数は整数係数に変えましょう。
　\( \begin{cases}
\hspace{4pt} 2\,x+8\,y=10　･･･③\\
\hspace{4pt}\displaystyle 4\,x+7\,y=-16　･･･④
\end{cases}\)
加減法で処理します。
　\(\hspace{14pt}4\,x+16\,y=20\\
\underline{-\,)\,4\,x+\hspace{4pt}7\,y=-16　}\\
\hspace{44pt}9\,y=36\\
\hspace{50pt}\underline{　y=4　}\)
\(\,①②③④\,\)のどれでも良いので代入して
　\(\hspace{10pt}\underline{　x=-11　}\)

\(\,①\,\)は両辺５倍して
　\(\hspace{10pt}x+4y=5\)
これを\(\,④\,\)とで代入法で処理しても良いです。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

迷うヒマがあれば処理を進めた方が早いです。
ただし、分数、小数のまま処理するのは時間がかかります。

(\(\,イ\,\))
２次方程式を解きます。
　\(\hspace{10pt}4\,x^2-x-2=0\)
因数分解できないので解の公式ですね。

⇒　２次方程式を解の公式で解く問題の見分け方と例題

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-1)\pm \sqrt{(-1)^2-4\times (4)\times (-2)}}{2\times 4}\\
&=&\frac{1\pm \sqrt{1+32}}{8}\\
&=&\underline{\underline{　\frac{1\pm \sqrt{33}}{8}　}}
\end{eqnarray}\)

２次方程式の解の公式の導き方は知っておいた方が良いです。
中学生でも機械的に数式処理すれば求まるので
入試問題になる可能性はあります。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

ただ、公式は導くより使えることの方が先です。

(\(\,ウ\,\))
２次関数の\(\,y\,\)の変域を求めます。
　関数：\(\displaystyle \,y=-\frac{1}{4}\,x^2\,\)
　\(\,x\,\)の変域：\(\,-2\,≦\,x\,≦\,4\,\)
　\(\,y\,\)の変域：\(\,a\,≦\,x\,≦\,b\,\)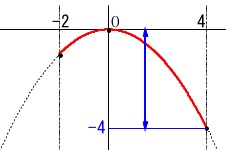簡単にでも良いのでグラフをかいて確認すると早いです。

\(\,y\,\)の変域は
　\(\hspace{10pt}-4\,≦\,y\,≦\,0\)
となるので
　\(\hspace{10pt}\underline{　a=-4\,,\,b=0　}\,\)
（最小と最大を逆にしないように注意しましょう）

最大値となるのは\(\,x=0\,\)のときの\(\,y=0\,\)です。
\(\,x=-2\,\)のときは\(\,y\,\)の変域に関係しません。

(エ)
方程式の文章題です。
　\(\,\mathrm{B}\,\)班の生徒は\(\,\mathrm{A}\,\)班より５人少ない。
　\(\,\mathrm{A}\,\)班はイスを３脚ずつ、\(\,\mathrm{B}\,\)班は４脚ずつ並べる。
　\(\,\mathrm{A}\,\)班の並べたイスの総数は\(\,\mathrm{B}\,\)班より３脚多かった。
　
１次方程式か連立方程式が考えられますが、
ここでは１次方程式で解いておきます。

\(\,\mathrm{A}\,\)班の生徒の人数を\(\,x\,\)とすると
\(\,\mathrm{B}\,\)班の正とは\(\,x-5\,\)となります。
　\(\begin{eqnarray}\displaystyle
3\times x&=&4\times (x-5)+3\\
3x&=&4x-20+3\\
x&=&\underline{　17　}
\end{eqnarray}\)

もちろん\(\,\mathrm{B}\,\)班の生徒数\(\,y\,\)として連立しても良いですよ。
やっていることは同じです。

(オ)
代入問題です。
　\(\hspace{10pt}x^2y+xy^2\\
=xy\,(\,x+y\,)\)

直接代入しても大した計算ではありませんが、
条件式が明らかに簡単になるといってくれているので
与式（求値式）を変形してから代入すると良いです。
　\(\begin{eqnarray}\displaystyle
xy&=&(\sqrt{6}+\sqrt{3})((\sqrt{6}-\sqrt{3})\\
&=&6-3\,\\
&=&\,\color{red}{3}\\
x+y&=&(\sqrt{6}+\sqrt{3})+((\sqrt{6}-\sqrt{3})\\
&=&\color{blue}{2\sqrt{6}}
\end{eqnarray}\)
よって
　\(\begin{eqnarray}\displaystyle
xy\,(\,x+y\,)&=&\color{red}{3}\times \color{blue}{2\sqrt{6}}\\
&=&\underline{　6\sqrt{6}　}
\end{eqnarray}\)

問２は以上です。

問３平面図形とデータ

問３は合同の証明と角度を求める問題、
それとヒストグラムの読み取り問題があります。

(\(\,ア\,\))
平行四辺形と二等辺三角形の性質を確認する問題です。

条件
　\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{CE}\,\)は\(\,\mathrm{∠BCD}\,\)の二等分線
　\(\,\mathrm{CF=DF}\,\)
　\(\,\mathrm{DG=DH}\,\)
それぞれの記号の位置は図１の通りです。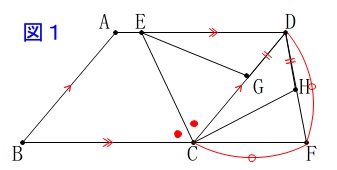(\(\,ⅰ\,\))
合同の証明です。
　\(\,\mathrm{△DEG}\,\)　≡　\(\,\mathrm{△DCH}\,\)
穴うめなので、
条件を整理してサッと終わらせます。平行四辺形であることから
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BF}\,\)
で錯角が等しくなるので
　\(\,\mathrm{△DCE}\,\)が二等辺三角形
になり、（角の二等分線と合わせて底角が等しくなる。）
また\(\,\mathrm{CF=DF}\,\)から
　\(\,\mathrm{△FCD}\,\)が二等辺三角形
であることが分かれば錯角が等しいことを利用して証明は終わります。

これが記述問題だと相当時間がかかるでしょうね。
（私なら問題にあるようなていねいな日本語はほとんど書きません。）
穴埋めなので［証明］を読みながら流れに沿って埋めてください。

この問題の意図は［証明］に書いてある流れを、
図の中で読み取ることです。

合同条件は
　\(\,\mathrm{DG=DH}\,\)
　\(\,\mathrm{DE=DC}\,\)　
　\(\,\mathrm{∠EDG=∠CDH}\,\)
から
　「２組の辺とその間の角がそれぞれ等しい。」

次に行きます。

(\(\,ⅱ\,\))
条件が加わって、角度を求めます。
長さは二等辺三角形という条件だけなので、
角の関係だけを見ていけば答えが出ます。
(\(\,ⅰ\,\))の条件は消えていませんよ。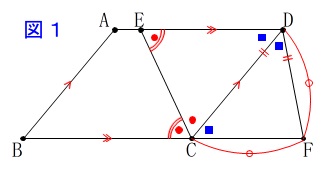加わる条件
　四角形\(\,\mathrm{CFDE}\,\)が平行四辺形になる。

このときの\(\,\mathrm{∠ABC}\,\)の大きさを求めます。
四角形\(\,\mathrm{CFDE}\,\)が平行四辺形になるなら錯角が等しくなり
　\(\,\mathrm{\color{blue}{∠CDF}=\color{blue}{∠ECD}}\,\)
となるので元の条件
　\(\,\mathrm{\color{red}{∠BCE}=\color{red}{∠DCE}}\,\)（角の二等分線）
から\(\,180°\,\)を３等分するので
　\(\,\mathrm{∠BCE=∠DEC=∠DCF}=60^{\circ}\,\)
このことから点\(\,\mathrm{E}\,\)は\(\,\mathrm{A}\,\)と重なり、
正三角形３つが合わさった形になります。
　\(\hspace{10pt}\mathrm{∠ABC}=\underline{　60^{\circ}　}\)

説明が足りないかもしれませんが、
加わった条件を利用して等しい角を図に書き足してみてください。
全ての頂角、底角が等しくなると分かります。

(\(\,イ\,\))
度数分布表とヒストグラムの問題です。

１問だけですが、
大学入試センターの共通テストを真似たみたいで結構重たいですよ。
マークシートを採用している都道府県は
センター傾向になる可能性が高いので注意しておくと良いです。
問題の善し悪しはどうでも良いですが、
ここは対策ページではないので対策はお任せします。
中学生ではできないと思うので学校の先生や塾の先生に教えてもらってください。
（会員は私がお答えします。）

条件は１年生の度数分布表と「説明」ですが、
読み取るだけでも結構大変な作業になります。
各学年で人数が違いますので一応確認しておきます。
　１年生３８人　２年生４０人　３年生４０人

簡単に解説しますので代表値を確認しながら進んでください。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

度数分布表と［説明］から
・中央値が同じ。
　１年：\(\,24\,\)　２年：\(\,24\,\)
（２年生のヒストグラムは\(\,1\,\)か\(\,2\,\)か\(\,5\,\)）
・３０回以上の割合
　１年：\(\,\displaystyle \frac{7}{38}\,\)　２年：\(\,\displaystyle \frac{x}{40}＜\,\frac{7}{38}\,\)
（明らかに\(\,2\,,\,5\,\)の度数は大きい。）
２年生のヒストグラムは\(\,\underline{　1　}\,\)です。

・最大値
　１年：\(\,\displaystyle 36\,\)　３年：\(\,\displaystyle 36\,\)
（３年生のヒストグラムは\(\,4\,\)か\(\,5\,\)か\(\,6\,\)）
・１４回未満の割合
　１年：\(\,\displaystyle \frac{4}{38}\,\)　３年：\(\,\displaystyle \frac{y}{40}＜\,\frac{4}{38}\,\)
（３年生のヒストグラムは\(\,5\,\)か\(\,6\,\)）
・最頻値
　２年生と３年生は等しい。
（ヒストグラムで比較するしかない。）
　２年：\(\,28\,\)
３年生のヒストグラムは\(\,\underline{　6　}\,\)　

階級が同じであるということは、
度数分布表では「見なし」があるので階級値が同じと見て良いです。

［説明］にあてはまる条件のヒストグラムを消去法で探しました。
この問題はセットで正解なので、
代表値、度数分布表、ヒストグラム全てを理解していないと正解にならない、
１問総出演問題でド欲張り問題です。
（平均値は関係ないけど来年は、、、かな？）

まだまだあります。

(\(\,ウ\,\))
角度を求める問題です。
円と平行線と二等分線があるので情報満載です。
分かる角度をどんどん書き込んで行きましょう。

条件
　\(\,\mathrm{ＢＥ}\,\)∥\(\,\mathrm{ＣＤ}\,\)
　\(\,\mathrm{ＡＤ}\,\)は\(\,\mathrm{∠ＢＤＥ}\,\)の二等分線
他の点の記号や線分は図２の通りです。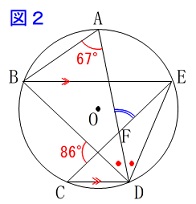円を平行線で切ると等脚台形ができるので簡単に終わりますが、
あてられた条件の性質を利用します。

１つの弧に対する円周角は等しく、
平行線の錯角は等しいので、
\(\,\color{blue}{●}\,\)の角は全て等しくなります。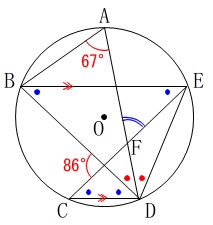三角形の内角の和でもなんでも良いですが、
　\(\hspace{10pt}\color{blue}{●}=43^{\circ}\)
が出てきます。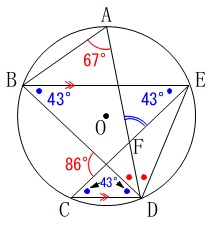また\(\,\mathrm{∠BAD=67^{\circ}}\,\)なので、
　\(\hspace{10pt}\mathrm{∠BED}=\color{red}{67^{\circ}}\,\) （円周角の定理）
これから\(\,\mathrm{∠BEC}=\color{blue}{43°}\,\)を引いて
　\(\hspace{10pt}\mathrm{∠CED=∠FED}=\color{magenta}{24^{\circ}}\)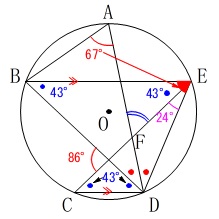三角形の内角の和から
　\(\hspace{10pt}\mathrm{∠BDE}=70^{\circ}\)
条件から\(\,\mathrm{AD}\,\)は\(\,\mathrm{∠BDE}\,\)の二等分線なので
　\(\hspace{10pt}\mathrm{∠ADE=∠FDE}=\color{green}{35^{\circ}}\)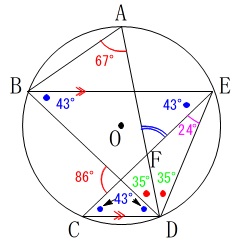よって
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AFE}&=&\mathrm{∠FED+∠FDE}\\
&=&\color{magenta}{24^{\circ}}+\color{green}{35^{\circ}}\\
&=&\underline{　59^{\circ}　}
\end{eqnarray}\)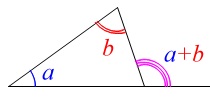全ての角が出せるので経路はどうでも良いから
分かる角度を次々と書き込んで行けば良いですよ。

会員の方は等脚台形から二等辺三角形を利用したと思います。
断然早いですし、事実なので構いません。

(\(\,エ\,\))
また円ですが(\(\,ウ\,\))と条件は違います。
三角形の面積を求める問題です。

条件
　線分\(\,\mathrm{AB}\,\)は円の直径
　\(\,\mathrm{BC}\,\)∥\(\,\mathrm{DE}\,\)
　\(\,\mathrm{AE=2\,,\,CE=1\,,\,DE=3}\,\)※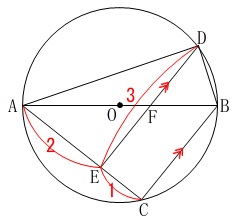
長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。

このとき\(\,\mathrm{△BDF}\,\)の面積を求めます。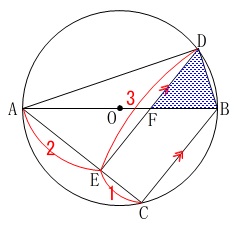長さや形が具体的に固定された形なので方針は人によって違ってくるでしょう。
ここでは条件の通りに分かることを書いて普通に解説します。

線分\(\,\mathrm{AB}\,\)は円の直径なので
　\(\hspace{4pt}\mathrm{∠ADB=∠ACB}=90^{\circ}\)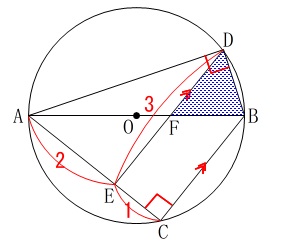平行線を利用して長方形を作りたいので、
点\(\,\mathrm{B}\,\)から\(\,\mathrm{DE}\,\)に垂線を下ろし交点を\(\,\mathrm{H}\,\)とします。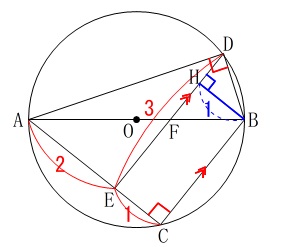このとき、
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△DBH}\,\)
　\(\,\mathrm{△AEF}\,\)　∽　\(\,\mathrm{△BHF}\,\)
となります。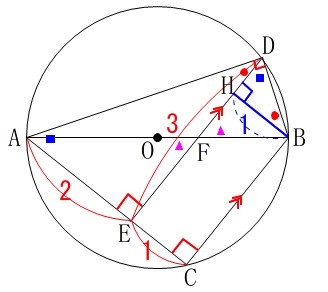相似条件はどちらも「２角がそれぞれ等しい」です。

少し説明を加えると
　\(\hspace{4pt}\mathrm{∠ADB=\color{red}{∠ADE}+\color{blue}{∠BDH}}=90^{\circ}\)
直角三角形の直角では無い2つの角を足すと\(\,90°\,\)なので
　\(\hspace{4pt}\mathrm{\color{red}{∠ADE}+\color{blue}{∠DAE}}=90^{\circ}\)
これから
　\(\hspace{10pt}\mathrm{\color{blue}{∠DAE}}=\mathrm{\color{blue}{∠BDH}}\)
なので
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△DBH}\,\)

もう一つは分かり易いでしょう。
　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{HB}\,\)
なので錯角、または対頂角が等しいので直角と合わせて
　\(\,\mathrm{△AEF}\,\)　∽　\(\,\mathrm{△BHF}\,\)

ここまでの相似は見抜けるようになっておきましょう。
難しいと感じる人は基本的な作業が足りていません。
問題の条件は必要だから与えてくれています。
利用するように進めてみてください。

さて、三角形の面積ですが、
相似比を利用するか具体的な面積計算をするかに分かれます。
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△DBH}\,\)
　\(\,\mathrm{△AEF}\,\)　∽　\(\,\mathrm{△BHF}\,\)
から分かる長さを出していきましょう。
全ての線分の長さが出ますが必要なところで止めれば良いです。

流れに乗って進めて行きます。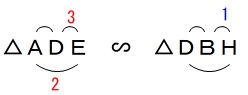　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△DBH}\,\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{DE:BH}&=&\mathrm{AE：DH}\\
\color{red}{3}:\color{blue}{1}&=&\color{red}{2}:\mathrm{DH}\\
3\times \mathrm{DH}&=&1\times 2\\
\mathrm{DH}&=&\color{blue}{\frac{2}{3}}
\end{eqnarray}\)
このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{EH}&=&\mathrm{DE-DH}\\
&=&3-\frac{2}{3}=\color{blue}{\frac{7}{3}}
\end{eqnarray}\)さらに、\(\,\mathrm{△AEF}\,\)　∽　\(\,\mathrm{△BHF}\,\)で
相似比が\(\,\mathrm{AE:BH}=\color{blue}{1}:\color{red}{2}\,\)なので
線分\(\,\mathrm{HF}\,\)の長さは\(\,\mathrm{HE}\,\)の\(\,\displaystyle \frac{1}{3}\,\)になります。
　\(\begin{eqnarray}\displaystyle
\mathrm{HF}&=&\frac{1}{2+1}\times \mathrm{HE}\\
&=&\frac{1}{3}\times \frac{7}{3}=\color{magenta}{\frac{7}{9}}
\end{eqnarray}\)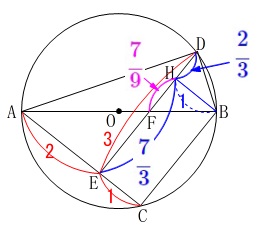あ、出ましたね。
　\(\begin{eqnarray}\displaystyle
\mathrm{△BDF}&=&\mathrm{DF}\times \mathrm{BH}\\
&=&\frac{1}{2}\times \left(\,\color{blue}{\frac{2}{3}}+\color{magenta}{\frac{7}{9}}\right)\times 1\\
&=&\frac{1}{2}\times \frac{13}{9}\times 1\\
&=&\underline{\underline{　\frac{13}{18}　}}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)
底辺と高さから三角形の面積を求めました。

線分\(\,\mathrm{BC}\,\)が求まるので三平方の定理から直径も求まります。
（おそらく三平方の定理を利用することを想定した問題です。）
\(\,\mathrm{△ADE}\,\)の面積が\(\,3\,\)と分かるので相似比から面積比を出して、
という方針でも良いですね。
めんど、、、長くなるので省略します。
解法は1つではないというのが分かっていれば良いです。

もっと詳しく解説しておきたいですが
ここまでにしておきます。

問３は以上です。
まだ半分ですか。
配点としては６割ありますがここでいったん区切らせて頂きます。

流れに乗って解いていけばそれほど時間はかからないと思いますが、
軽い問題ばかりでもないので受験生にとっては楽ではないでしょうね。

問４問５問６の解説

問４以降の解説ですが、違うページになります。

問４は関数と面積比、問５は確率の応用問題、
問６は立体図形の問題となっています。

⇒　2022年度神奈川県公立高校入試の数学の問題と解説【後半】

後半が全て難しいわけではないので
とれるところを確実にとっていけば良いですよ。

⇒　神奈川県公立高校入試の数学過去問の問題と解答解説

神奈川県の公立入試は条件の読み取りを重視しているようです。
ただし、基本的なことを広い範囲でおさえておくことは、
全国の都道府県どこでも同じです。