令和4年(2022年)度三重県公立入試【前期】数学の問題と解説

令和4年度(2022年)に行われた三重県の【前期】公立高校入試の数学の問題と解説です。
前期と後期にそれほど差があるわけではありません。
基本事項と基本作業ををおさえておくことは必須です。
後期の数学を先に解説してありますのでそちらも参考にしてください。

令和4年度(2022年)三重県公立高校入試【前期】数学の問題

前期日程の数学問題です。

⇒　令和4年(2022年)度三重県公立高校入試【前期】数学の問題

試験時間は４５分です。

令和4年度(2022年)三重県公立入試【前期】数学の解説

大問が\(\,\color{black}{\fbox{1}}\,\)から\(\,\color{black}{\fbox{5}}\,\)まであります。

三重県は例年出題範囲や問題レベルに偏りがありません。
基本だけではないので基本問題を早めに済ませ
標準応用問題にできるだけ時間を作りたいところです。
ただ、５０点満点なので各問の配点が小さく見えますが
応用問題をとることより基本問題を落とさないことを大切にしましょう。

第１問

計算問題から作図まで１０題あります。

(1)
正の数負の数の計算です。
　\(\hspace{10pt}-3^2+4\times (-2)\\
=-9-8\\
=\underline{　-17　}\)

足し算より掛け算が先です。

(2)
文字式の計算です。
　\(\hspace{10pt}(4x+5)-(x-3)\\
=4x+5-x+3\\
=\underline{　3x+8　}\)

ミスを減らすため２行目は書いた方が確実です。

(3)
文字式の等式処理です。
分数を無くして処理した方が早いです。
　\(\begin{eqnarray}\displaystyle
c&=&\frac{a+b}{5}\\
5c&=&a+b\\
a+b&=&5c\\
b&=&5c-a
\end{eqnarray}\)

答え　\(\hspace{4pt}\displaystyle \underline{　b=5c-a　}\)

学校で習ったりや参考書に書いてあることもあるので
アルファベット順と思い込んでいる人もいるでしょう。
　\(\hspace{10pt}\displaystyle \underline{　b=-a+5c　}\)
でも良いですよ。

(4)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} y=x-3　･･･①\\
\hspace{4pt} 4x+5y=30　･･･②
\end{cases}\)　
\(\,①\,\)の\(\,x\,\)を移項して加減法でも良いですが
素直に代入法で解いておきます。
①を②に代入して
　\(\begin{eqnarray}\displaystyle
4x+5(x-3)&=&30\\
4x+5x-15&=&30\\
9x&=&45\\
x&=&5
\end{eqnarray}\)
これを②に代入して
　\(\hspace{10pt}y=(5)-3\,=\,2\)

答え　\(\hspace{10pt}\underline{　x=5\,,\,y=2　}\)

(5)
無理数の計算です。
　\(\hspace{10pt}\displaystyle \color{red}{\sqrt{12}}+\color{blue}{\frac{1}{\sqrt{3}}}\\
\displaystyle =\color{red}{2\sqrt{3}}+\color{blue}{\frac{\sqrt{3}}{\sqrt{3}\times \sqrt{3}}}\\
\displaystyle =2\sqrt{3}+\frac{\sqrt{3}}{3}\\
\displaystyle =\frac{6\sqrt{3}+\sqrt{3}}{3}\\
\displaystyle =\underline{\underline{　\frac{7\sqrt{3}}{3}　}}\)

暗算できる程度ではありますが、
素因数分解と分母の有理化はていねいにやった方が良いです。

(6)
２次方程式を解きます。

まとまりを作っても良いですが展開してしまった方が早いでしょう。
　\(\begin{eqnarray}\displaystyle
(x+2)^2&=&4x+13\\
x^2+4x+4&=&4x+13\\
x^2-9&=&0\\
(x+3)(x-3)&=&0\\
x&=&\underline{　-3\,,\,3　}
\end{eqnarray}\)

３行目以降は
　\(\begin{eqnarray}\displaystyle
x^2&=&9\\
x&=&\pm 3
\end{eqnarray}\)
とした方が良いのではないかと感じる人もいるかもしれませんね。
もちろん構いませんよ。
方程式を解くときの基本は、
全ての項を左辺に集めることなので基本通りやりました。

また、（かっこ）でまとめられてる部分があるので
　\(\begin{eqnarray}\displaystyle
(x+2)^2&=&4x+13\\
(x+2)^2&=&4(x+2)+5\\
\end{eqnarray}\)
と変形することで進めたりもできますが、
考えすぎですね。笑
\(\hspace{4pt}x+2=a\,\)とすると
　\(\begin{eqnarray}\displaystyle
a^2&=&4a+5\\
a^2-4a-5&=&0\\
(a+1)(a-5)&=&0\\
a&=&-1\,,\,5\\
x+2&=&-1\,,\,5\\
x&=&-3\,,\,3
\end{eqnarray}\)

方程式の解き方もひとつではありません。
見直しも必要なので思いついた方法で突き進みましょう。

(7)
変化の割合を求めます。
　\(\hspace{4pt}\displaystyle \color{red}{(\,変化の割合\,)}=\frac{　\color{magenta}{(\,y\,の増加量\,)}　}{　\color{blue}{(\,x\,の増加量\,)}　}\)

関数\(\,\displaystyle y=\frac{12}{x}\,\)において
　\(\hspace{4pt}(\,\color{blue}{-6}\,,\,\color{magenta}{-2}\,)\)
　\(\hspace{4pt}(\,\color{blue}{-3}\,,\,\color{magenta}{-4}\,)\)
となるので
　\(\begin{eqnarray}\displaystyle
(\,変化の割合\,)&=&\frac{\color{magenta}{-4-(-2)}}{\color{blue}{-3-(-6)}}\\
&=&\frac{-2}{3}\\
&=&\underline{\underline{　-\frac{2}{3}　}}
\end{eqnarray}\)

増加量を計算するとき引く順番を間違えないようにしましょう。
答えのマイナス符号は分子にあっても良いです。

(8)
球の体積を求めます。

求める球の体積を\(\,V\,\)とすると
　\(\begin{eqnarray}\displaystyle
V&=&\frac{4}{3}\,\pi\times (\,3\,)^3\\
&=&\underline{　36\,\pi　}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

中学生では公式を導けないので覚えて使うしかないです。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

代表値が小学校の内容に下りたように、
微分積分の基礎が中学生の内容になれば別ですけど。

(9)
角度を求めます。
長方形の折り返しなので分かり易いですね。

条件
　長方形\(\,\mathrm{ABCD}\,\)の対角線\(\,\mathrm{AC}\,\)で折る。
　\(\,\mathrm{∠BAC=58^{\circ}}\,\)
記号は図の通りとなります。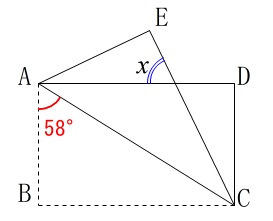折り返された図形と折り返す前の図形は同じなので、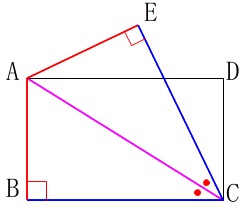角度も辺の長さも同じだから合同な図形があります。
長方形の場合二等辺三角形もあるので分かり易いですね。
会員の方は『平行と合同』カード「合同発見シリーズ」で見慣れているでしょうから即答でしょう。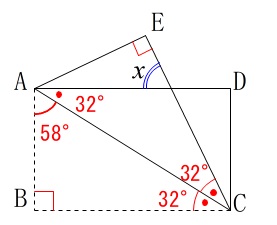全ての角が求まりますので、
順序はどうでも良いから分かる角度を書き出して行けば良いです。
　\(\hspace{10pt}∠\,x\,=\underline{　64^{\circ}　}\)

ちなみに、
この場合の\(\,x\,\)は位置を表していて角度ではありません。
角度を表すときは\(\,∠x\,\)となります。

(10)
おうぎ形の作図です。
中心を探せば良いのですが条件の角度の使い方が問題です。

中心角が\(\,110°\,\)となるおうぎ形なので、
２つありそうですが１つでいいそうです。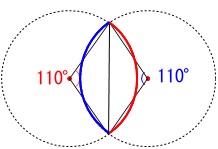問題にある条件は
　\(\hspace{4pt}\mathrm{∠ABC}=90^{\circ}\)
　\(\hspace{4pt}\mathrm{∠BAC}=70^{\circ}\)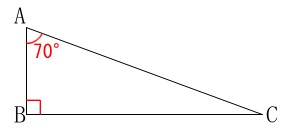中心角\(\,110°\,\)がどことつながるかわかりにくいですね。

先ずは完成形をイメージしてみましょう。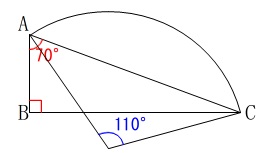こんな感じです。

先ず、
　弦\(\,\mathrm{AC}\,\)の垂直二等分線　\(\,･･･\color{red}{①}\,\)
上に中心\(\,\mathrm{O}\,\)はあります。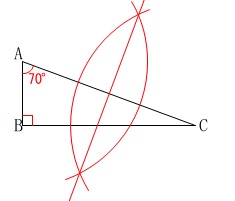さらに、
半径は等しく\(\,\mathrm{OC=OA}\,\)なので
　\(\,\mathrm{△OAC}\,\)は二等辺三角形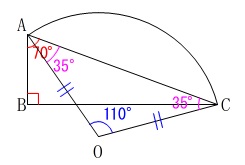になるので底角は
　\(\hspace{4pt}\displaystyle \frac{180^{\circ}-110^{\circ}}{2}=35^{\circ}\)
これは
　\(\,\mathrm{∠BAC}\,\)の角の二等分線　\(\,･･･\color{blue}{②}\,\)
で作れます。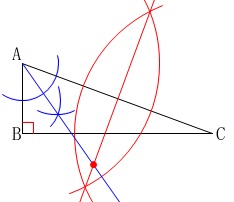中心\(\,\mathrm{O}\,\)は\(\,\color{red}{①}\color{blue}{②}\,\)の交点になります。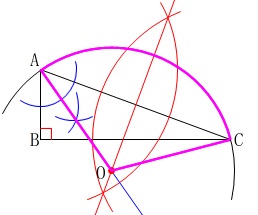中心\(\,\mathrm{O}\,\)、半径\(\,\mathrm{OC}\,\)の円を描いておうぎ形のできあがりです。
※
一度で\(\,\mathrm{C\,,\,A}\,\)できっちり弧を止める作図は実際は不可能に近いです。
\(\,\mathrm{C}\,\)から始める弧と\(\,\mathrm{A}\,\)から始める弧をつなげれば良いです。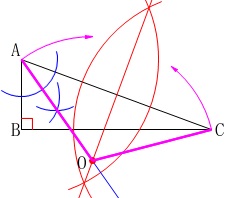三重県の解答例を見てみると、手順は同じですが垂直二等分線はどうやって引いたか不明です。

\(\,\color{black}{\fbox{1}}\,\)は以上です。

第２問

\(\color{black}{\fbox{2}}\)
度数分布表の読み取りと、
文字式を利用する文章題の２題があります。

(1)
生徒数は\(\,\mathrm{A}\,\)組\(\,27\,\)人と\(\,\mathrm{B}\,\)組\(\,23\,\)人です。
　\(\begin{array}{|c|c|c|} \hline
　階級　&　\mathrm{A}\,組　&　\mathrm{B}\,組　\\ \hline
\,15\,～\,20\, & 2 & 1 \\ \hline
\,20\,～\,25\, & 5 & \color{black}{\fbox{(ア)}} \\ \hline
\,25\,～\,30\, & 6 & 4 \\ \hline
\,30\,～\,35\, & 7 & 3 \\ \hline
\,35\,～\,40\, & 3 & 10 \\ \hline
\,40\,～\,45\, & 3 & 0 \\ \hline
\,45\,～\,50\, & 1 & \color{black}{\fbox{(イ)}} \\ \hline
　計　 & 27 & 23 \\ \hline
\end{array}\)
\(\,①\,\)
\(\,\mathrm{A}\,\)組の最頻値は、
\(\,30\,～\,35\,\)の階級の階級値なので\(\,\underline{　32.5　}(\mathrm{kg})\,\)

最頻値は代表値の１つです。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

小学生のあなた、「最頻値」読めますか？
小学校の算数の内容ですよ。
※
ちなみにこの問題は高校入試の問題ですが、
最頻値の読み方をひらがなで加えてくれています。

\(\,②\,\)
２つの組の範囲と中央値が同じときを考えます。
　\(\color{red}{\fbox{(範囲)=(最大値)－(最小値)}}\)
　\(\,\mathrm{A}\,\)組の範囲：\(\,47.5-17.5\,=\,30.0\,\)
だから\(\,\mathrm{B}\,\)組も範囲は同じ\(\,30.0\,\)になるはずなので
\(\color{black}{\fbox{イ}}\)の度数は１以上でなければなりません。
（もしも度数が\(\,0\,\)なら範囲は\(\,20.0\,\)になってしまいます。）

中央値はデータを小さい順に並べたときのまん中に位置する値です。
　\(\,\mathrm{A}\,\)組：\(\,27\,\)人なので\(\,14\,\)人目の\(\,\color{red}{32.5}\,\)
\(\,\mathrm{B}\,\)組の中央値が同じ\(\,\mathrm{32.5}\,\)なら、
\(\,23\,\)人中\(\,12\,\)人目のデータが\(\,30\,～\,35\,\)の階級になければなりません。
\(\color{black}{\fbox{(ア)}}\)が、
　\(\,3\,\)のとき中央値は\(\,37.5\,\)
　\(\,4\,\)のとき中央値は\(\,\color{red}{32.5}\,\)
合計人数の関係からここまでしかありませんが、
（\(\color{black}{\fbox{イ}}\)の度数は１以上で残りが\(\,22\,\)人以下だから。）
　\(\,5\,\)のとき中央値は\(\,\color{red}{27.5}\,\)でダメです。

\(\color{black}{\fbox{ア}}\)の度数が\(\,5\,\)のとき、
\(\color{black}{\fbox{イ}}\)の度数は\(\,0\,\)になるので範囲が同じにならないことも確認しておいてください。

(2)
文字式の文章題です。
連立方程式のようですが条件が１つしかないので、
整数比でしか分からない問題です。

条件をまとめておきます。
　入園料：大人\(\,1000\,\)円、子ども\(\,200\,\)円
　クーポン\(\,\mathrm{A}\,\)：入園料から\(\,20\,\)％引き
　クーポン\(\,\mathrm{B}\,\)：大人\(\,1\,\)人につき子ども\(\,2\,\)人が無料

クーポン\(\,\mathrm{B}\,\)についてわかりにくいかもしれませんが、
大人を\(\,x\,\)人とすると子ども\(\,2x\,\)人分が無料だということです。
（子どもの人数は大人の２倍以上という条件が問題にあります。）

\(\,①\,\)
大人\(\,2\,\)人、子ども\(\,7\,\)人がクーポン\(\,\mathrm{A}\,\)を利用すると
全員が\(\,20\,\)％引きになるので
　\(\hspace{4pt}\displaystyle (\,1000\times 2+200\times 7\,)\times \frac{80}{100}\\
\displaystyle =(\,2000+1400\,)\times \frac{80}{100}\\
\displaystyle =3400\times \frac{80}{100}\\
=\underline{　2720　}(円)\)

大人と子ども別々に計算しても良いですよ。

\(\,②\,\)
大人\(\,x\,\)人、子ども\(\,y\,\)人がクーポン\(\,\mathrm{B}\,\)を利用すると
子どもの\(\,2x\,\)人分が無料になるので
入園する子どもの人数を\(\,y-2x\,\)と考えれば
　\(\hspace{10pt}\displaystyle 1000\times x+200\times (y-2x)\\
=1000\,x+200\,y-400\,x\\
=\underline{　600\,x+200\,y　}(円)\)

\(\,③\,\)
クーポン\(\,\mathrm{A}\,\)、クーポン\(\,\mathrm{B}\,\)を利用して、
入園料がどちらも同じになるときです。

大人に人数を\(\,x\,\)人、子どもの人数を\(\,y\,\)人としておきます。
（文字は何でも良いですよ。）

クーポン\(\,\mathrm{A}\,\)を利用したときの入園料は、
大人\(\,1\,\)人\(\,800\,\)円、子ども\(\,1\,\)人\(\,160\,\)円なので
　\(\hspace{10pt}\displaystyle 800\,x+160\,y\)

クーポン\(\,\mathrm{B}\,\)を利用したときの入園料は、
\(\,②\,\)から
　\(\hspace{10pt}\displaystyle 600\,x+200\,y\)

これらが等しいとき
　\(\begin{eqnarray}\displaystyle
800\,x+160\,y&=&600\,x+200\,y\\
200\,x&=&40\,y\\
5\,x&=&y
\end{eqnarray}\)

答え　\(\hspace{10pt}\underline{　1:5　}\)

子どもが大人の\(\,5\,\)倍の人数のときに等しくなるということになります。

\(\color{black}{\fbox{2}}\,\)は以上です。

第３問

\(\color{black}{\fbox{3}}\)
確率の問題ですが、文字式と規則性の融合された問題になります。

先ずは〈ルール〉を確認しておきましょう。
　\(\,(ⅰ)\,\)自然数を１つ決め、\(\,\mathrm{A}\,\)とする。
　\(\,(ⅱ)\,\)
　\(\hspace{10pt}\mathrm{A}\,\)が奇数のとき\(\,\mathrm{B=A+\color{red}{1}\,,\,C=B+\color{red}{1}}\,\)
　\(\hspace{10pt}\mathrm{A}\,\)が偶数のとき\(\,\mathrm{B=A+\color{blue}{2}}\,,\,\mathrm{C=B+\color{blue}{2}}\,\)
　\(\,(ⅱ)\,\)
　\(\hspace{10pt}\mathrm{D=A+B}\,,\,\mathrm{E=B+C}\,,\,\mathrm{F=D+E}\)
これだけ見てもわかりにくいので具体的に見ていきますが、
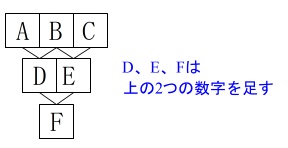\(\,\mathrm{D\,,\,E\,,\,F}\,\)は上の数字を足しています。

\(\,①\,\)
\(\,\mathrm{A=5}\,\)のとき（奇数なので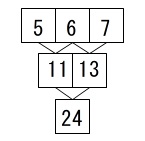）\(\,\mathrm{B\,,\,C}\,\)を書き込めば後は足し算です。

答え　\(\,\mathrm{F}=\underline{　24　}\,\)

\(\,②\,\)
\(\,\mathrm{A}\,\)が偶数\(\,m\,\)のときです。
\(\,①\,\)でやったように\(\,\mathrm{A\,,\,B\,,\,C}\,\)を書き込みます。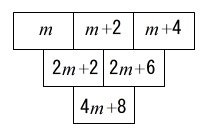後は上の2つを足すことの繰り返しです。
答え　\(\hspace{4pt}\mathrm{F}=\underline{　4m+8　}\)

\(\,③\,\)
\(\,\mathrm{F}\,\)の数にならないものを全て選びます。
　\(\hspace{4pt}ア．120　イ　123　ウ．124　エ．128　オ．129\)

「\(\,\mathrm{A}\,\)がどのような数でも、\(\,\mathrm{F}\,\)にならないもの」を選ぶので
偶数の場合と奇数の場合とどちらかで表せれば除外します。

偶数の場合\(\,②\,\)から\(\,\mathrm{F}\,\)は\(\,4\,\)の倍数
かつ\(\,m\,\)が偶数なので\(\,8\,\)の倍数は全て表せます。
だからアとエは除外できます。
逆に言えば\(\,\mathrm{A}\,\)が偶数のときは\(\,8\,\)の倍数以外は表せません。

\(\,\mathrm{A}\,\)が奇数のときに表せない数を探しましょう。
残り３つなので全て調べた方が分かり易いでしょう。
（ここでは\(\,4\,\)の倍数以外は調べません。）

\(\,n\,\)を奇数とすると\(\,②\,\)のときと同じように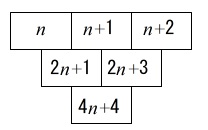　\(\hspace{4pt}\mathrm{F}=4n+4\)
奇数の場合も\(\,4\,\)の倍数です。

奇数は表せないので少なくともイとオは答えです。
残りはウの\(\,124\,\)ですが
　\(\begin{eqnarray}\displaystyle
4\,n+4&=&124\\
4\,n&=&120\\
n&=&30
\end{eqnarray}\)
となり\(\,n\,\)が奇数であることに不適です。

よって、\(\,\mathrm{F}\,\)にならない数は
　\(\hspace{10pt}\underline{　イ　ウ　オ　}\)

文字式の置き方を
　奇数：\(\,2n-1\,,\,2n+1\,\)
　偶数：\(\,2\,n\,\)
などとしても良いですよ。

\(\,②\,\)で表した\(\,\mathrm{F}\,\)を\(\,4\,\)の倍数とみるだけでは足りませんので、
注意しておきましょう。

\(\,②\,\)で「偶数のとき」とあるので「奇数のときは？」と考えるのが自然でしょう。

(2)
さいころ２つの確率です。

大小２つののさいころを同時に投げて、
出た目の和の数だけ玉を移動させます。
条件
　袋\(\,\mathrm{A}\,\)：\(\,12\,\)個の玉
　袋\(\,\mathrm{B}\,\)：\(\,m\,\)個の玉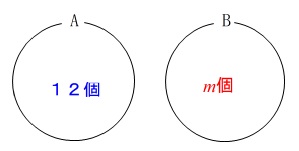２つのさいころを投げ出た目の和だけ\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)に移動させ、
移動後の袋\(\,\mathrm{A}\,\)の玉の数を\(\,x\,\)、袋\(\,\mathrm{B}\,\)の玉の数を\(\,y\,\)とする。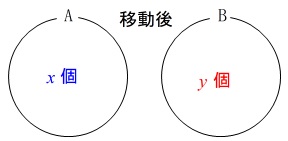考えにくいかもしれないので
出た目を\(\,\color{red}{a}\,,\,\color{blue}{b}\,\)とでもすると分かり易いかもしれません。
出た目の和は\(\hspace{4pt}\color{red}{a}+\color{blue}{b}\,\)となるので
　\(\hspace{10pt}x=12-(\color{red}{a}+\color{blue}{b})\,,\,y=m+(\color{red}{a}+\color{blue}{b})\)
となります。

樹形図で良いですが表で和を見ておきます。
赤青どちらが大小でも構いませんよ。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \,\color{red}{1}\, & \,\color{red}{2}\, & \,\color{red}{3}\, & \color{red}{4} & \color{red}{5} & \color{red}{6 }\\ \hline
\, \color{blue}{1}\, & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline
\, \color{blue}{2}\, & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline
\color{blue}{3} & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline
\color{blue}{4} & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline
\color{blue}{5} & 6 & 7 & 8 & 9 & 10 & 11 \\ \hline
\color{blue}{6} & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline
\end{array}\)
①
\(\,m=0\,\)のとき\(\,x=y\,\)となる確率を求めます。

\(\,m=0\,\)のときというのは移動前\(\,\mathrm{B}\,\)には玉は無かったということです。
なので\(\,x=y\,\)というのは
　\(\begin{eqnarray}\displaystyle
12-(\color{red}{a}+\color{blue}{b})&=&0+(\color{red}{a}+\color{blue}{b})\\
12&=&2(\color{red}{a}+\color{blue}{b})\\
\color{red}{a}+\color{blue}{b}&=&6
\end{eqnarray}\)
簡単に言えば\(\,12\,\)個から\(\,6\,\)個移せば同じ数になるということですね。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \,\color{red}{1}\, & \,\color{red}{2}\, & \,\color{red}{3}\, & \color{red}{4} & \color{red}{5} & \color{red}{6 }\\ \hline
\, \color{blue}{1}\, & 2 & 3 & 4 & 5 & \color{magenta}{6} & 7 \\ \hline
\, \color{blue}{2}\, & 3 & 4 & 5 & \color{magenta}{6} & 7 & 8 \\ \hline
\color{blue}{3} & 4 & 5 & \color{magenta}{6} & 7 & 8 & 9 \\ \hline
\color{blue}{4} & 5 & \color{magenta}{6} & 7 & 8 & 9 & 10 \\ \hline
\color{blue}{5} & \color{magenta}{6} & 7 & 8 & 9 & 10 & 11 \\ \hline
\color{blue}{6} & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline
\end{array}\)
\(\,36\,\)通りの出方があって\(\,5\,\)通りが和が\(\,6\,\)になります。

答え　\(\hspace{4pt}\displaystyle \underline{　\frac{5}{36}　}\)

もちろん樹形図で\(\,x=y\,\)となる場合を探していっても良いです。
進めて行けば規則性に気がつくでしょう。

\(\,②\,\)
今度は確率が分かっているときの\(\,m\,\)の値を求めます。

条件
　\(\hspace{4pt}x=y\,\)となるときの確率が\(\,\displaystyle \frac{1}{12}\,\)

このときの\(\,m\,\)の値を求めます。
\(\,m\,\)は移動前に\(\,\mathrm{B}\,\)の袋にあった玉の数です。

\(\hspace{4pt}x=y\,\)となるのは、
袋\(\,\mathrm{A}\,\)と袋\(\,\mathrm{B}\,\)の移動後の数が同じということで、
例えば\\(\,①\,\)で求めた(\,\mathrm{A}\,\)が\(\,12\,\)個、\(\,\mathrm{B}\,\)が\(\,0\,\)個の場合は
\(\,6\,\)個移動すれば等しくなりますが確率が違います。
だから\(\,m=0\,\)ではない、ということが分かります。

これを順に調べていっても良いですね。
そうすることで規則性が見えてきます。
・\(\hspace{4pt}m=1\,\)のとき、
合計\(\,13\,\)個で奇数なので2つに分けて等しくなることはありません。
・\(\hspace{4pt}m=2\,\)のとき、
\(\,\mathrm{A}\,\)に\(\,12\,\)個、\(\,\mathrm{B}\,\)に\(\,2\,\)個あるので\(\,5\,\)個移動して等しくできます。
ただし、そのときの確率は
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \,\color{red}{1}\, & \,\color{red}{2}\, & \,\color{red}{3}\, & \color{red}{4} & \color{red}{5} & \color{red}{6 }\\ \hline
\, \color{blue}{1}\, & 2 & 3 & 4 & \color{magenta}{5} & 6 & 7 \\ \hline
\, \color{blue}{2}\, & 3 & 4 & \color{magenta}{5} & 6 & 7 & 8 \\ \hline
\color{blue}{3} & 4 & \color{magenta}{5} & 6 & 7 & 8 & 9 \\ \hline
\color{blue}{4} & \color{magenta}{5} & 6 & 7 & 8 & 9 & 10 \\ \hline
\color{blue}{5} & 6 & 7 & 8 & 9 & 10 & 11 \\ \hline
\color{blue}{6} & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline
\end{array}\)
　\(\hspace{10pt}\displaystyle \frac{4}{36}=\frac{1}{9}\)
となるので条件に適していません。

順に調べて行けば答えは出ますよ。
ここでは逆に確率から考えましょう。

確率が\(\displaystyle \,\frac{1}{12}=\frac{3}{36}\,\)になるのは、
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \,\color{red}{1}\, & \,\color{red}{2}\, & \,\color{red}{3}\, & \color{red}{4} & \color{red}{5} & \color{red}{6 }\\ \hline
\, \color{blue}{1}\, & 2 & 3 & \color{magenta}{4} & 5 & 6 & 7 \\ \hline
\, \color{blue}{2}\, & 3 & \color{magenta}{4} & 5 & 6 & 7 & 8 \\ \hline
\color{blue}{3} & \color{magenta}{4} & 5 & 6 & 7 & 8 & 9 \\ \hline
\color{blue}{4} & 5 & 6 & 7 & 8 & 9 & \color{magenta}{10} \\ \hline
\color{blue}{5} & 6 & 7 & 8 & 9 & \color{magenta}{10} & 11 \\ \hline
\color{blue}{6} & 7 & 8 & 9 & \color{magenta}{10} & 11 & 12 \\ \hline
\end{array}\)
移動する玉の数が\(\,4\,\)か\(\,10\,\)のときです。
\(\,10\,\)個移動して同じになることはないので、
（移動前\(\,\mathrm{A}\,\)には\(\,12\,\)個しかない。）
移動する玉の数が\(\,4\,\)個のとき、
つまり、\(\,\mathrm{A}\,\)の袋にある\(\,12\,\)個から\(\,8\,\)個になるときで、
\(\,4\,\)個移動して\(\,\mathrm{B}\,\)も\(\,8\,\)個になるということなので
　\(\hspace{10pt}m=\underline{　4　}\)

文字式でおいた形で見ると移動するのは出た目の和で
　\(\begin{eqnarray}\displaystyle
12-(a+b)&=&m+(a+b)\\
12-4&=&m+4\\
m&=&\underline{　4　}
\end{eqnarray}\)
※
\(\,a+b=10\,\)の場合は
　\(\begin{eqnarray}\displaystyle
12-(a+b)&=&m+(a+b)\\
12-10&=&m+10\\
m&=&-8
\end{eqnarray}\)
となり不適です。

順に調べて行く方針でも良いですが、
玉の合計が偶数のときだけ調べるにしても時間的に厳しいでしょうね。

\(\color{black}{\fbox{3}}\,\)は以上です。

第４問

\(\color{black}{\fbox{4}}\,\)は動点２つと面積の問題です。
動点問題のポイントは変化のあるところで区分け、ですね。

条件
　１辺が\(\,6\,\)の正方形\(\,\mathrm{ABCD}\,\)がある。
　点\(\,\mathrm{P}\,\)は毎秒\(\,2\,\)で\(\,\mathrm{B\rightarrow C\rightarrow D\rightarrow A\rightarrow B}\,\)と移動。
　点\(\,\mathrm{Q}\,\)は毎秒\(\,1\,\)で\(\,\mathrm{C\rightarrow D\rightarrow A}\,\)と移動。
　移動開始から\(\,x\,\)秒後の\(\,\mathrm{△BPQ}\,\)の面積を\(\,y\,\)とする。※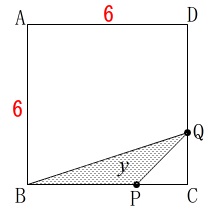
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。

点\(\,\mathrm{P}\,\)は\(\,24\,\)の長さを毎秒\(\,2\,\)で移動するので\(\,12\,\)秒で\(\,\mathrm{B}\,\)に到達、
点\(\,\mathrm{Q}\,\)は\(\,12\,\)の長さを毎秒\(\,1\,\)で移動するので\(\,12\,\)秒で\(\,\mathrm{A}\,\)に到達、
ということは頭の隅でもおいておきましょう。

変化するポイントとしては
　\(\,\mathrm{P}\,\)が正方形の頂点に到達する\(\,3\,,\,6\,,\,9\,\)
　\(\,\mathrm{Q}\,\)が正方形の頂点\(\,\mathrm{D}\,\)に到達する\(\,6\,\)
となるので区間分けすると
　\(\hspace{4pt}0\,≦\,x\,≦\,3\)
　\(\hspace{4pt}3\,≦\,x\,≦\,6\)
　\(\hspace{4pt}6\,≦\,x\,≦\,9\)
　\(\hspace{4pt}9\,≦\,x\,≦\,12\)
の４つになりますが、問題に合わせて見ていきましょう。

(1)
２秒後の\(\,\mathrm{△BPQ}\,\)の面積です。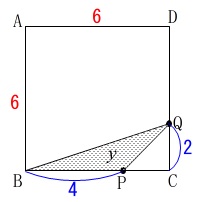２秒後は点\(\,\mathrm{P}\,\)は\(\,\mathrm{BC}\,\)上、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{DC}\,\)上にあります。
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 4\times 2\\
&=&\underline{　4　}(\mathrm{cm^2})
\end{eqnarray}\)

(2)
\(\hspace{4pt}3\,≦\,x\,≦\,6\,\)のときの\(\,y\,\)の式を求めます。

\(\,x=3\,\)のとき（動き出してから\(\,3\,\)秒後）
　点\(\,\mathrm{P}\,\)は点\(\,\mathrm{C}\,\)
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{DC}\,\)の中点
にあります。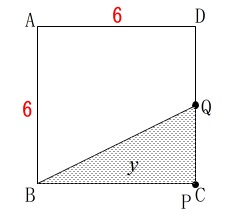ここから両点とも\(\,\mathrm{D}\,\)に向かうので、
\(\,\mathrm{△BPQ}\,\)の面積\(\,y\,\)は底辺\(\,\mathrm{PQ}\,\)、高さ\(\,\mathrm{BC=6}\,\)から表すことができます。

底辺\(\,\mathrm{PQ}\,\)の長さを\(\,x\,\)で表すのですが、
線分\(\,\mathrm{CQ}\,\)の長さが\(\,x\,\)であることは説明不要でしょう。線分\(\,\mathrm{CP}\,\)の長さが分かれば底辺\(\,\mathrm{PQ}\,\)が分かります。

線分\(\,\mathrm{CP}\,\)は\(\,\mathrm{P}\,\)が移動した長さ\(\,\color{blue}{2x}\,\)から、
正方形の１辺\(\,\color{red}{6}\,\)を引けば良いので、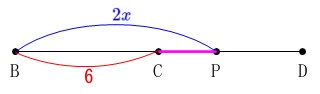\(\hspace{4pt}\mathrm{CP}=\color{magenta}{2x-6}\,\)
となります。
（直線で動いていると考えると分かり易いですよ。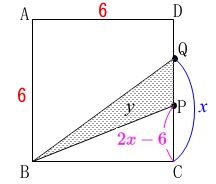）これから
　\(\begin{eqnarray}\displaystyle
\mathrm{PQ}&=&\mathrm{CQ-CP}\\
&=&\color{blue}{x}-(\,\color{magenta}{2x-6}\,)\\
&=&6-x
\end{eqnarray}\)
よって求める\(\,\mathrm{△BPQ}\,\)の面積\(\,y\,\)は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (6-x)\times 6\\
&=&18-3x
\end{eqnarray}\)
※
\(\,\mathrm{P}\,\)は\(\,\mathrm{Q}\,\)に近づくので面積は減っていくことと、
６秒後に\(\,\mathrm{P\,,\,Q}\,\)は重なるので面積が\(\,0\,\)になることを確認しておくと良いです。

(3)
\(\,\mathrm{△BPQ}\,\)の面積\(\,y\,\)の変化を表すグラフを選びます。

(2)で\(\,3\,≦\,x\,≦\,6\,\)のとき減少していることは確認していて、
\(\,6\,\)秒後は\(\,\mathrm{P\,,\,Q}\,\)ともに点\(\,\mathrm{D}\,\)にいるので
面積が\(\,0\,\)になるから\(\,イ\,\)か\(\,エ\,\)ですが、
\(\,9\,\)秒後は\(\,\mathrm{P}\,\)は点\(\,\mathrm{A}\,\)、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{AD}\,\)の中点にいるので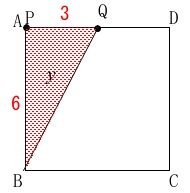面積は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 3\times 6\\
&=&9
\end{eqnarray}\)
となるはずなので答えは\(\,\underline{　イ　}\,\)です。

(4)
\(\,9\,≦\,x\,≦\,12\,\)の場合を考えます。

点\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)上に、
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{AD}\,\)上にあります。繰り返しになりますが、
位置関係は変化のあこるところで区分けして確認することがポイントです。

長さの求め方は(2)と同じように考えます。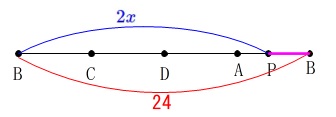　\(\hspace{4pt}\mathrm{BP}=24-2\,x\)
同じように高さとなる\(\,\mathrm{AQ}\,\)は、
　\(\hspace{4pt}\mathrm{AQ}=12-x\)
（これは練習として自分で出してください。）
このとき\(\,\mathrm{△BPQ}\,\)の面積\(\,y\,\)は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (24-2x)\times (12-x)\\
&=&(12-x)^2
\end{eqnarray}\)
これが\(\,7\,\)となるときなので
　\(\begin{eqnarray}\displaystyle
(12-x)^2&=&7\\
x&=&12\pm \sqrt{7}
\end{eqnarray}\)
※
２次方程式を解く段階は省略していますが、
展開して解の公式でも、
平方完成されているので平方根型でもどちらでも良いです。

\(\,9\,≦\,x\,≦\,12\,\)の場合を考えているので
　\(\hspace{10pt}x=\underline{　12-\sqrt{7}　}\)

\(\,2=\sqrt{4}\,,\,3=\sqrt{9}\,\)なので
\(\hspace{10pt}2\,＜\,\sqrt{7}\,＜\,3\)
だから問題の条件に合っています。

全ての場合を関数にしておけば考えることも少ないですが、
時間的に厳しくなりそうなら問題の順序通りに進めた方が良いでしょう。
　
\(\color{black}{\fbox{4}}\,\)は以上です。

第５問

\(\color{black}{\fbox{5}}\)
平面図形の問題と回転体の問題です。

(1)
正三角形がふたつあり一部が重なっている条件があります。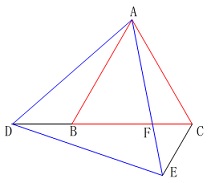問題の条件通りに図がありますので確認してください。

\(\,①\,\)
合同の証明です。
　\(\,\mathrm{△ABD}\,\)≡\(\,\mathrm{△ACE}\,\)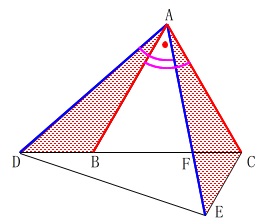会員の人は平面図形『合同発見シリーズ』で慣れているでしょう。
瞬間でできていると思うので省略します。
合同条件は
　『２組の辺とその間の角がそれぞれ等しい。』
です。

合同や相似の証明は図の中で終わらせておくことです。

\(\,②\,\)
長さと面積比を求める２題です。
\(\,①\,\)で見た条件は変わりませんが長さの条件が加わります。

相似に気がつくかどうかなので簡単に済ませます。

条件
　\(\,\mathrm{AC=6\,,\,CE=3}\,\)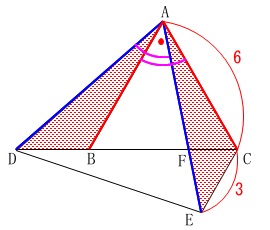※長さの単位は\(\,\mathrm{cm}\,\)です。
\(\,(ⅰ)\,\)
線分\(\,\mathrm{BF}\,\)の長さを求めますが、
\(\,①\,\)で証明した合同から対応する角も等しいので
　\(\hspace{10pt}\mathrm{∠ADC=∠AEC}\)
で円周角が等しくなるので四角形\(\,\mathrm{ADEC}\,\)は円に内接しています。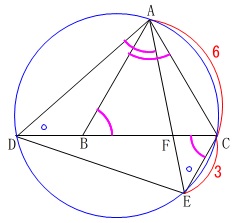正三角形の１つの角は\(\,60°\,\)なので
　\(\hspace{10pt}\mathrm{∠DAE=∠ABC=∠DCE}=60^{\circ}\)
錯角が等しくなるので\(\,\mathrm{AB}\,\)∥\(\,\mathrm{CE}\,\)となり
対頂角と合わせて相似条件がそろうので
　\(\,\mathrm{△ABF}\,\)　∽　\(\,\mathrm{△ECF}\,\)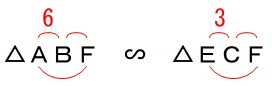相似比が
　\(\hspace{10pt}\mathrm{AB:EC}=6:3=2:1\)
なので
　\(\hspace{10pt}\mathrm{BF:CF}=2:1\)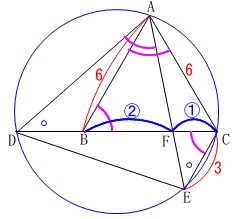線分\(\,\mathrm{BC}\,\)は正三角形の１辺なので\(\,\color{red}{6}\,\)だから
　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&\frac{2}{1+2}\times \mathrm{BC}\\
&=&\frac{2}{3}\times \color{red}{6}\\
&=&\underline{　4　}(\,\mathrm{cm}\,)
\end{eqnarray}\)

\(\,(ⅱ)\,\)
次は面積比ですが\(\,(ⅰ)\,\)で長さが出ているので合同、相似と合わせて考えます。

\(\,①\,\)で証明した合同から
　\(\hspace{10pt}\,\mathrm{BD=CE=3}\,\)
また\(\,(ⅰ)\,\)で見つけた相似から
　\(\hspace{10pt}\mathrm{AF:EF}=2:1\)
これは三角形の高さの比に利用します。

底辺を\(\,\mathrm{DC}\,\)とみると
\(\,\mathrm{△ADC}\,\)の高さは\(\,\mathrm{△ECD}\,\)の高さの\(\,2\,\)倍です。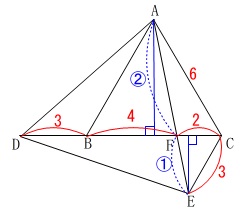また、\(\,(ⅰ)\,\)から\(\,\mathrm{BF=4}\,,\,\mathrm{CF=2}\,\)です。

\(\,\mathrm{△FEC}\,\)と四角形\(\,\mathrm{ADEC}\,\)の面積比なので、
\(\,\mathrm{△FEC}\,\)を\(\,\color{red}{①}\,\)としたいところですが、
\(\,\mathrm{BD=3}\,\)となっている時点で分数が出てくることが予想されるので、
\(\,\mathrm{△FEC=\color{red}{②}}\,\)としておきます。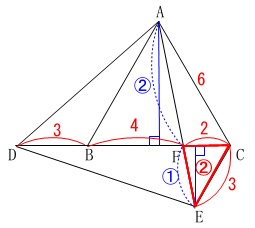底辺や高さの比から細かく分けると
　\(\hspace{4pt}\mathrm{△DFE}=\color{red}{⑦}\)
　\(\hspace{4pt}\mathrm{△AFC}=\color{red}{④}\)
　\(\hspace{4pt}\mathrm{△ABF}=\color{red}{⑧}\)
　\(\hspace{4pt}\mathrm{△ADB}=\color{red}{⑥}\)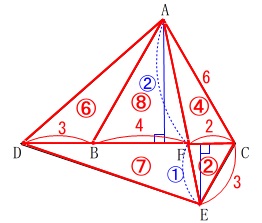よって、
\(\,\mathrm{△FEC}\,\)の面積を\(\,S_1\,\)、四角形\(\,\mathrm{ADEC}\,\)の面積を\(\,S_2\,\)とすると
　\(\begin{eqnarray}\displaystyle
S_1:S_2&=&\color{red}{②}:(\,\color{red}{②}+\color{red}{⑦}+\color{red}{④}+\color{red}{⑧}+\color{red}{⑥}\,)\\
&=&\underline{　2:27　}
\end{eqnarray}\)

\(\,\mathrm{△ADF}\,\)の面積を分けずに\(\,\color{red}{⑭}\,\)としても少し早いですね。

もちろん\(\,\mathrm{△FEC=1}\,\)として分数で計算しても結果は同じです。

(2)
直角三角形の回転体（円すい）の表面積を求めます。

展開図ですが見取り図が先ですね。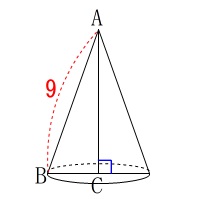展開図において中心角が\(\,120°\,\)です。このときおうぎ形の弧の長さは
　\(\hspace{10pt}\displaystyle 2\times \pi \times 9\times \frac{120}{360}\\
\displaystyle =\color{blue}{6\,\pi}\)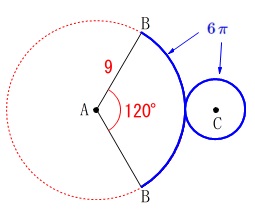これは底面の円周に等しいので半径が\(\,3\,\)となり、
底面の面積は
　\(\hspace{10pt}\pi\times (\,3\,)^2=\color{magenta}{9\,\pi}\)
また側面となるおうぎ形の面積は
　\(\hspace{10pt}\displaystyle \pi\times \,(\,9\,)^2\times \frac{120}{360}=\color{magenta}{27\,\pi}\)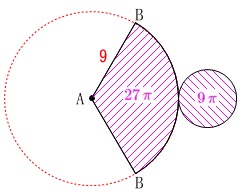
⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

よって、求める表面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\color{magenta}{9\,\pi}+\color{magenta}{27\,\pi}\\
&=&\underline{　36\,\pi　}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

以上です。
※
確認していないのでミスがあればご指摘ください。
よろしくお願い致します。

後期日程も同じように時間に余裕があるわけではありません。

⇒　令和4年度(2022年)三重県公立入試【後期】数学の問題と解説（後半）

基本をしっかりおさえて、
方針が立つまでどんどん手を動かしましょう。

⇒　三重県公立高校入試の数学の問題と解説

解説ページなので詳しい対策は書きませんが、
広い範囲の基礎を確実に身に付けておく、それが対策となります。
（当たり前すぎますね。）

『覚え太郎』シリーズが最適です。