2022年（令和4年）度群馬県公立高校入試【前期】数学の問題と解説

2022年（令和4年）度の群馬県公立高校入試における【前期】数学の問題と解説です。
例年通り偏りの無い基本中心の問題で構成されていますので、
数学全体の復習のひとつにして本番で満点目指してがんばりましょう。
他の都道府県の人も基本確認の良い練習になりますよ。

2022年（令和4年）度群馬県公立高校入試【前期】数学の問題

前期の数学問題です。

⇒　2022年（令和4年）度群馬県公立高校入試【前期】数学の問題

\(\,1\,\)から\(\,4\,\)の大問4つは例年通りの構成で、
問題量として多くはありません。

2022年（令和4年）度群馬県公立高校入試【前期】数学の解説

早速解説を進めて行きますが、全体を通じてポイントは１つです。
問題量も多くなく基本中心の出題なので、
ミスには気をつけておきましょう。

第１問

\(\,\large{1}\,\)
基本確認問題が(1)から(7)までありますが、
くれぐれもミスには気をつけて確実に取っておきましょう。

(1)
計算問題が\(\,①\,\)から\(\,⑥\,\)まであります。
\(\,①\,\)
　\(\hspace{10pt}1-(-4)\\
=1+4\\
=\underline{　5　}\)

負の数を引くことは足すことになります。

\(\,②\,\)
　\(\hspace{10pt}a+7a\\
=\underline{　8a　}\)

文字式でも計算法則は変わりません。
同類項は係数の足し算でまとめます。

\(\,③\,\)
　\(\hspace{10pt}2x\times (-x)\\
=\underline{　-2x^2　}\)

全体の符号に注意ですね。

\(\,④\,\)
　\(\hspace{10pt}3(x+y)-4(x-y)\\
=3x+3y-4x\color{red}{+}4y\\
=\underline{　-x+7y　}\)

２行目は暗算しない方がミスは減りますよ。

\(\,⑤\,\)
　\(\hspace{10pt}\displaystyle 4a^2b\div a\\
\displaystyle =\frac{4a^2b}{a}\\
=\underline{　4ab　}\)

割り算は逆数の掛け算で処理できるので
　\(\hspace{10pt}\displaystyle 4a^2b\div a\\
\displaystyle =4a^2b\times \frac{1}{a}\\
=\underline{　4ab　}\)
ということと同じですが、
ややこしい計算ほど上の処理（\(\,\div\,\)の直後を全て分母に）をした方が見やすいです。

\(\,⑥\,\)
　\(\hspace{10pt}\displaystyle \frac{2}{\sqrt{2}}+\sqrt{18}\\
\displaystyle =\frac{2}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}+\sqrt{2\times 3^2}\\
\displaystyle =\frac{2\sqrt{2}}{2}+3\sqrt{2}\\
=\sqrt{2}+3\sqrt{2}\\
=\underline{　4\sqrt{2}　}\)

分母の有理化、素因数分解をやっています。
無理数の計算は慣れの程度で暗算度合いが変わりますので、
本番までに練習しておくと良いです。
ただ、過度の暗算はミスにつながりますので注意しましょう。

(2)
文字式を展開します。
　\(\hspace{10pt}(x-3y)(x+3y)\\
=\underline{　x^2-9y^2　}\)

展開公式
　\(\hspace{10pt}\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用していますが文字式の展開は、
あれこれ考えるより突っ走ってもなんとかなります。
　\(\hspace{10pt}(x-3y)(x+3y)\\
=x^2+3xy-3xy-9y^2\\
=\underline{　x^2-9y^2　}\)

見直しに利用しても良いですね。

(3)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} x+y=-1　･･･①\\
\hspace{4pt} x-2y=-13　･･･②
\end{cases}\)

加減法でも代入法でも良いです。
　\(\hspace{16pt}x+\,y\,=-1\\
\hspace{2pt}\underline{-\,)\,x-2y=-13}\\
\hspace{34pt}3y=12\\
\hspace{38pt}y=\,4\)
これを\(\,①\,\)に戻して
　\(\begin{eqnarray}\displaystyle
x+(4)&=&-1\\
x&=&-5
\end{eqnarray}\)
答え
　\(\hspace{10pt}\underline{　x=-5\,,\,y=4　}\)

連立方程式を解くときの基本は一文字消去です。

(4)
対称移動（線対称移動）先の点を答えます。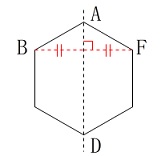線対称なので\(\,\mathrm{AD}\,\)を折り目として折り曲げるということです。

答え　\(\,\underline{　点\,\mathrm{F}　}\,\)

(5)
２次方程式を解きます。
　\(\hspace{4pt}x^2+x-12=0\)

左辺が因数分解できそうですね。
　\(\begin{eqnarray}\displaystyle
x^2+x-12&=&0\\
(x+4)(x-3)&=&0\\
x&=&-4\,,\,3
\end{eqnarray}\)

２次方程式を全て解の公式で解いていると時間がかかりすぎます。

⇒　2次方程式の因数分解を利用する解き方のコツと注意点

文章題では特に、
解が整数になりやすいので因数分解から試すと良いですよ。

(6)
平行な直線では傾きが同じです。
切片を\(\,b\,\)とおいて
　\(\hspace{10pt}y=3x+b\)

これが\(\,(\,2\,,\,4\,)\,\)を通るので
　\(\begin{eqnarray}\displaystyle
4&=&3\times (2)+b\\
b&=&-2
\end{eqnarray}\)

答え　\(\hspace{4pt}\underline{　y=3x-2　}\)

(7)
直角三角形の面積を求めます。
斜辺と１辺が分かっているので高さとなるもう一つの辺を、
三平方の定理で求めましょう。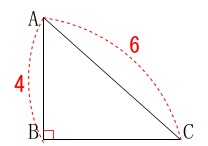　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2+BC^2}&=&\mathrm{AC^2}\\
4^2+\mathrm{BC^2}&=&6^2\\
\mathrm{BC^2}&=&20\\
\mathrm{BC}&=&\pm 2\sqrt{5}
\end{eqnarray}\)
\(\,\mathrm{BC}\,\)は長さなので\(\,\mathrm{BC\,＞\,0}\,\)だから
　\(\hspace{4pt}\mathrm{BC}=2\sqrt{5}\)
よって三角形\(\,\mathrm{ABC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AB}\times \mathrm{BC}\\
&=&\frac{1}{2}\times 4\times 2\sqrt{5}\\
&=&\underline{　4\sqrt{5}　}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

\(\,\large{1}\,\)は以上です。
配点の半分近くがあるので、
確実に、ミスができるだけ無いようにしましょう。

第２問

データ、確率、円周角、文字式の利用の４題があります。
(1)
平均を求めます。
仮平均を利用するか、データそのものを表すかですが、
分かり易いのは実回数を書き出すことです。

基準は\(\,\mathrm{A}\,\)の回数で\(\,30\,\)回です。
　\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline
生徒 & \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{D} & \mathrm{E} & \mathrm{F} & \mathrm{G} & \mathrm{H} & \mathrm{I} & \mathrm{J}\\ \hline
　\mathrm{A}\,との差　& 0 & -5 & +3 & -1 & +3 & -1 & +2 & -3 & -2 & -6 \\ \hline
回数 & 30 & 25 & 33 & 29 & 33 & 29 & 32 & 27 & 28 & 24 \\ \hline
\end{array}\)

\(\,\mathrm{A}\,\)を\(\,0\,\)回と見なすと平均は、
基準との差の平均から
　\(\hspace{4pt}\displaystyle \frac{-10}{10}=-1　･･･①\)
本当は\(\,\mathrm{A}\,\)の回数は\(\,30\,\)回なので求める平均は
　\(\hspace{10pt}\displaystyle 30-1=\underline{　29　}　(\,回\,)\)

これが仮平均を利用した平均値の求め方です。
\(\,①\,\)を求めるとき平均値からのズレの和は、
それぞれを足すと\(\,0\,\)になる組み合わせを消していくと計算が楽です。
例えば、\(\,\mathrm{C}\,\)と\(\,\mathrm{H}\,\)でも良いですし、
\(\,\mathrm{B\,,\,C\,,\,D\,,\,E}\,\)でも良いです。
足すと\(\,0\,\)になるので残りを計算すれば早いです。

基準値からのズレは考えにくい、
という人は実回数を書き出して計算すれば良いですよ。
足し算にちょっと時間はかかるけど確実です。
（その場合計算ミスの無いように慎重に足し算しましょう。）
　\(\hspace{10pt}\displaystyle \frac{290}{10}=29\)
試験会場ではこのくらいの作業はなんとも思わない、
それくらいの気持ちで取り組めば満点も見えてきます。
泥くさい？大歓迎です。
そこから始めれば良いです。

(2)
確率の定義の確認です。

さいころの１つの目が出る確率が\(\displaystyle \,\frac{1}{6}\,\)というのは、
無限に回数をこなしたときの理論値です。

何回投げても毎回毎回何が出るかは、
前の回の出た目には関係ありません。

答え　\(\,\underline{　エ　}\,\)

偶数が出る確率も、\(\,3\,\)以下の目が出る確率も\(\,\displaystyle \frac{1}{2}\,\)です。

ちなみに\(\,ウ\,\)も計算が必要ですね。
　\(\hspace{10pt}\displaystyle \frac{1}{6}\times \frac{1}{6}=\frac{1}{36}\)

アとイについては起こることもありますが、
必ず正しいとは言えません。

(3)
円周角の問題です。

角度を求めるときは分かるところから書き込んで行きましょう。
何か１つヒントになる要素を見つけることができればほぼ解決します。線分\(\,\mathrm{AB}\,\)、\(\,\mathrm{BC}\,\)を引いて、
直径\(\,\mathrm{BD}\,\)に対する円周角が\(\,90°\,\)になるので分かる角度を書き込んでみてください。
　\(\hspace{10pt}\mathrm{∠ACD=∠ABD}=\underline{　48^{\circ}　}\)

問題に書いてある「直径\(\,\mathrm{BD}\,\)」に対する円周角は\(\,90°\,\)、
これが大きなヒントです。

(4)
文字式で条件を満たす答えを求めます。

求めたいのは１年生のときに借りた本なので、
一年生のときに借りた本の冊数を\(\,a\,\)とすると
（文字は何でも良いです。）
　\(\begin{array}{|c|c|c|c|} \hline
　学年　 &　 1 　&　 2　 & 　3　 \\ \hline
　借りた冊数　 & a & a+6 & 2\,a \\ \hline
\end{array}\)
合計が\(\,50\,\)冊なので、
　\(\begin{eqnarray}\displaystyle
a+(a+6)+2a&=&50\\
4a&=&44\\
a&=&11
\end{eqnarray}\)
答え　\(\,\underline{　11　}(\,冊\,)\,\)

比較があるときは基準になっているものを文字でおきますが、
ここでは基準も１年生のときに借りた本の冊数なので
求めるものと一致しています。

\(\,\large{2}\,\)は以上です。

第３問

\(\,\large{3}\,\)
平行四辺形と相似です。
(1)
図のように平行四辺形\(\,\mathrm{ABCD}\,\)の辺\(\,\mathrm{BC}\,\)上に点\(\,\mathrm{E}\,\)があり、
線分\(\,\mathrm{AE}\,\)と線分\(\,\mathrm{BD}\,\)との交点を\(\,\mathrm{F}\,\)とするとき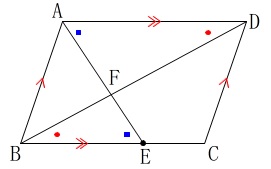　\(\,\mathrm{△FAD}\,\)　∽　\(\,\mathrm{△FEB}\,\)
を証明します。

（証明）
　\(\,\mathrm{△FAD}\,\)と\(\,\mathrm{△FEB}\,\)において
平行四辺形の対辺はそれぞれ平行で、
錯角が等しくなるので、
　\(\hspace{10pt}\mathrm{∠FAD=∠FEB}　･･･①\)
　\(\hspace{10pt}\mathrm{∠FDA=∠FBE}　･･･①\)
\(\,①②\,\)から
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△FAD}\,\)　∽　\(\,\mathrm{△FEB}\,\)
（終わり）

証明は図の中で終わらせておきましょう。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明の書き方は決まっているわけではありません。
自分でかきやすい方法で証明すれば良いですよ。

相似条件の１つには対頂角を使ってももちろん構いません。

第４問

\(\,\large{4}\,\)
関数の基本確認問題と回転体の体積を求めます。

条件
　関数\(\,y=ax^2\,\)のグラフ上に\(\,y\,\)座標が等しい２点\(\,\mathrm{A\,,\,B}\,\)がある。
　関数\(\,y=-3x^2\,\)のグラフ上に\(\,y\,\)座標が等しい２点\(\,\mathrm{C\,,\,D}\,\)がある。
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,3\,\)、\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,1\,\)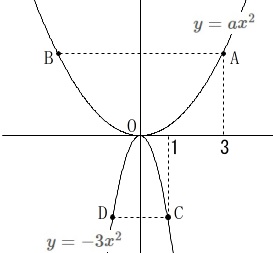問題に合わせてでも良いですが、
条件から分かることを書き込んでおくと早いです。

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,3\,\)なので
　\(\hspace{4pt}\mathrm{A}\,(\,3\,,\,9a\,)\)
点\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)座標が等しいので放物線の対称性から
　\(\hspace{4pt}\mathrm{B}\,(\,-3\,,\,9a\,)\)
点\(\,\mathrm{C}\,\)の\(\,x\,\)座標が\(\,1\,\)なので　
　\(\hspace{4pt}\mathrm{C}\,(\,1\,,\,-3\,)\)
点\(\,\mathrm{D}\,\)は\(\,\mathrm{C}\,\)と\(\,y\,\)座標が等しいので放物線の対称性から
　\(\hspace{4pt}\mathrm{D}\,(\,-1\,,\,-3\,)\)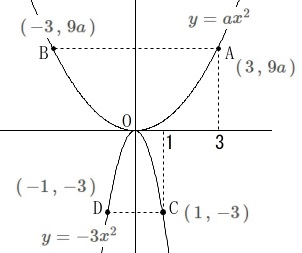問題に入りましょう。
(1)
点\(\,\mathrm{D}\,\)の座標は
　\(\hspace{10pt}\mathrm{D}\,\underline{　(\,-1\,,\,-3\,)　}\)

(2)
比例定数と回転体の体積です。
\(\,①\,\)
比例定数を\(\,a\,\)を求めますが、
変化の割合が条件として与えられています。

関数\(\,y=ax^2\,\)において
　「\(\,x\,\)の値が\(\,3\,\)から\(\,6\,\)まで増加したとき変化の割合が\(\,\color{magenta}{3}\,\)」

２点を座標で表すと
　\(\hspace{4pt}(\,\color{red}{3}\,,\,\color{red}{9\,a}\,)\)
　\(\hspace{4pt}(\,\color{blue}{6}\,,\,\color{blue}{36\,a}\,)\)

変化の割合は
　\(\hspace{10pt}\displaystyle (\,変化の割合\,)=\frac{　y\,の増加量　}{　x\,の増加量　}\)
なので
　\(\begin{eqnarray}\displaystyle
\frac{\color{blue}{36\,a}-\color{red}{9\,a}}{\color{blue}{6}-\color{red}{3}}&=&\color{magenta}{3}\\
9\,a&=&3\\
a&=&\underline{　\frac{1}{3}　}
\end{eqnarray}\)

これで関数が決定しました。
　\(\hspace{10pt}\displaystyle y=\frac{1}{3}\,x^2\)
このとき
　\(\hspace{4pt}\mathrm{A}\,(\,-3\,,\,3\,)\,,\,\mathrm{B}\,(\,3\,,\,3\,)\)
となるので座標上に書き込んでおきます。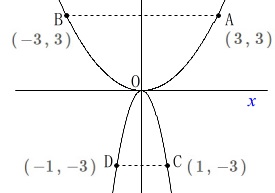
\(\,②\,\)
回転体の体積を求めますが、
回転の軸が\(\,x\,\)軸なので間違えないようにしましょう。

線分\(\,\mathrm{AC}\,\)と線分\(\,\mathrm{BD}\,\)の\(\,x\,\)軸との交点は、
それぞれ\(\,\mathrm{E\,,\,F}\,\)です。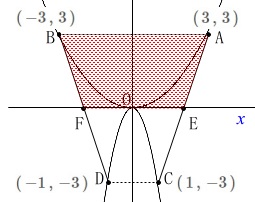このとき四角形\(\,\mathrm{ABFE}\,\)を\(\,x\,\)軸を回転の軸として回転させた体積を求めます。円柱から円すい２つをくり抜いた形ですね。
円すいは左右対称なので１つ体積を求めて２倍します。

立体のイメージができたところで具体的な長さを出していきましょう。
　円柱の底面の半径は\(\,\mathrm{A}\,\)の\(\,y\,\)座標で\(\,3\,\)
　円柱の高さは線分\(\,\mathrm{AB}\,\)の長さで\(\,6\,\)
　円すいの底面の半径は円柱と同じで\(\,3\,\)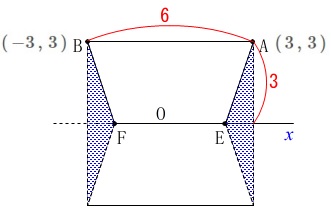円すいの高さは点\(\,\mathrm{E}\,\)の座標が必要です。

２点\(\,\mathrm{A\,,\,C}\,\)を通る直線は
　\(\hspace{10pt}y=3x-6\)
となるので\(\,x\,\)軸上の点\(\,\mathrm{E}\,\)の座標は\(\,y=0\,\)から
　\(\hspace{4pt}\mathrm{E}\,(\,2\,,\,0\,)\)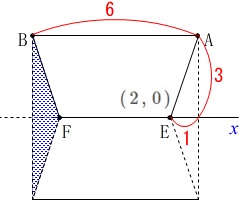このことから円すいの高さは\(\,\color{red}{1}\,\)です。

よって求める回転体の体積\(\,V\,\)は
円柱の体積から２つの円すいの体積を引いて
　\(\begin{eqnarray}\displaystyle
V&=&\pi\times (3)^2\times 6-\frac{1}{3}\times \pi\times (3)^2\times 1\times 2\\
&=&54\,\pi-6\,\pi\\
&=&\underline{　48\,\pi　}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

点\(\,\mathrm{C\,,\,D}\,\)の\(\,y\,\)座標の絶対値が、
点\(\,\mathrm{A\,,\,B}\,\)と\(\,y\,\)座標より大きい場合はややこしい計算が待っていそうですが、
同じか、小さい場合は中に含まれるので四角形\(\,\mathrm{ABDC}\,\)を回転させても同じ体積になります。
（あまり深く考えなくて良いですよ。）

以上です。

⇒　（後期未公開）

後期試験も解説しますので参考にしてください。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

前期においては基本を広い範囲で聞いてくるので、
過去問を数年分見て確認しておきましょう。