2022年（令和4年）度群馬県公立高校【後期】入試数学の問題と解説の解説です。
計算の基礎から関数、図形と偏りの無い大問で６つの構成は例年通りです。
規則性の問題もあり差はつくけど計算が複雑とかではなくて、
きっちりと数学の基礎がおさえられているか確認できる問題です。
2022年（令和4年）度群馬県公立高校【後期】入試数学の問題
2022年（令和4年）度群馬県公立入試【後期選抜】数学の問題です。
⇒ 2022年（令和4年）度群馬県公立入試【後期選抜】数学の問題
大問で\(\,1\,\)から\(\,6\,\)まであります。
2022年（令和4年）度群馬県公立高校【後期】入試数学の解説
しっかりとした基礎とある程度の作業ができれば高得点が狙える問題です。
ポイントだけをおさえて解説を進めます。
別解などはあまり書きませんが、
数学の問題を解く方法は１つではありませんので、
あなたが解いた方法が、
ここで示す方法と違ったとしても気にしないでください。
第１問計算が主な小問集合
\(\,\large{1}\,\)
(1)から(9)までありますが、
基本問題ばかりなのでミスをしないように注意しましょう。
(1)
計算問題が３つあります。
①
\(\hspace{10pt}3-7\\
=\underline{ -4 }\)
②
\(\hspace{10pt}3x+2(x-1)\\
=3x+2x-2\\
=\underline{ 5x-2 }\)
③
\(\hspace{10pt}12ab^3\div 4ab\\
\displaystyle =\frac{12ab^3}{4ab}\\
=\underline{ 3\,b^2 }\)
無理に暗算しなくても良いので確実にいきましょう。
(2)
方程式を２つ解きます。
①
１次方程式です。
\(\begin{eqnarray}\displaystyle
4x+5&=&x-1\\
4x-x&=&-1-5\\
3x&=&-6\\
x&=&\underline{ -2 }
\end{eqnarray}\)
②
２次方程式です。
\(\hspace{10pt}x^2-3x+1=0\)
左辺が因数分解できないので解の公式ですね。
\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm \sqrt{(-3)^2-4\times 1\times 1}}{2\times 1}\\
&=&\frac{3\pm \sqrt{9-4}}{2}\\
&=&\underline{\underline{ \frac{3\pm \sqrt{5}}{2} }}
\end{eqnarray}\)
解の公式で全ての２次方程式は解けますが、
（係数に偶数がある場合など）
因数分解を利用する方法から試しましょう。
(3)
因数分解です。
\(\hspace{10pt}x^2-16y^2\)
２つの項が２乗の形になるので公式が使えます。
\(\hspace{10pt}x^2-16y^2\\
=x^2-(4y)^2\\
=\underline{ (x+4y)(x-4y) }\)
展開は無理矢理でも計算でできますが、
因数分解の公式は多くはないので覚えておいた方が良いですよ。
(4)
代入問題です。
\(\hspace{10pt}(2a+b)-(a+4b)\\
=2a+b-a-4b\\
=a-3b\\
\displaystyle =(3)-3\times \left(\frac{1}{3}\right)\\
=3-1\\
=\underline{ 2 }\)
値の代入は与式（求値式）を簡単にしてから、
最後に代入した方が楽なことが多いです。
⇒ 式の計算(中学2年) 文字式に数値を代入する問題を解くときのポイント
(5)
角度を求めます。
「\(\,\mathrm{AB=AC}\,\)の二等辺三角形」
という条件を見逃さないようにしましょう。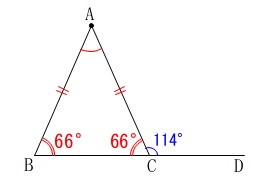
\(\hspace{10pt}\mathrm{∠BAC}=\underline{ 48^{\circ} }\)
求め方は三角形の内角の和でも良いですし、
\(\hspace{4pt}\mathrm{∠ACD=∠ABC+∠BAC}\)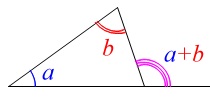
を利用しても良いです。
分かるところの角を書き込んで行けば良いですが、
条件１つ加えればほとんどの問題での方向性が見えてきます。
(6)
（解）として求め方も書きます。
一例
（解）
先ず関数\(\,y=ax^2\,\)の比例定数を決定する。
\(\,x=-2\,\)のとき\(\,y=8\,\)ということから
\(\begin{eqnarray}\displaystyle
8&=&a\times (-2)^2\\
a&=&2
\end{eqnarray}\)
よって関数は\(\,y=2\,x^2\,\)であり\(\,x=3\,\)のとき
\(\begin{eqnarray}\displaystyle
y&=&2\times (3)^2\\
&=&\underline{ 18 }
\end{eqnarray}\)
解の書き方は好きにしていいですよ。
決まりはありませんので求めた方法を文字にすれば良いです。
(7)
１回だけ赤玉を取り出す確率を求めます。
樹形図で良いですよ。
ここでは表にしておきます。
\(\begin{array}{|c|c|c|} \hline
１回目 & ２回目 & \\ \hline
赤 & 赤 & \\ \hline
\color{red}{赤} & 青 & ○ \\ \hline
\color{red}{赤} & 白 & ○ \\ \hline
青 & \color{red}{赤} & ○ \\ \hline
青 & 青 & \\ \hline
青 & 白 & \\ \hline
白 & \color{red}{赤} & ○ \\ \hline
白 & 青 & \\ \hline
白 & 白 & \\ \hline
\end{array}\)
出方は全部で９通り、そのうち４通りあるので
\(\hspace{4pt}\displaystyle \underline{\underline{ \frac{4}{9} }}\)
１回目２回目はそれぞれ単独で成り立つ事象なので
「１回目赤、２回目青か白」
または
「１回目青か白、２回目赤」
という出方があるので
\(\hspace{10pt}\displaystyle \frac{1}{3}\times \frac{2}{3}+\frac{2}{3}\times \frac{1}{3}\\
\displaystyle =\underline{\underline{ \frac{4}{9} }}\)
としても良いです。
(8)
平面図は真横から見た図、平面図は真上から見た図です。
ア：四角すい
イ：球
ウ：三角すい
エ：円すい
オ：三角柱
答え \(\,\underline{ ウ }\,\)
(9)
相対度数折れ線の読み取りです。
度数合計が違うので度数に違いがあるとことに注意しましょう。
答え \(\,\underline{ ウ }\,\)
割合は相対度数で見ても同じなので、
\(\,\mathrm{A}\,\)：\(\,0.10\,+\,0.10\,=\,0.20\)
\(\,\mathrm{B}\,\)：\(\,0.20\,+\,0.15\,=\,0.35\)
\(\,\mathrm{B}\,\)中学校の方が大きい割合になります。
\(\,\large{1}\,\)は以上です。
第２問数の世界と性質
\(\,\large{2}\,\)
数の分類です。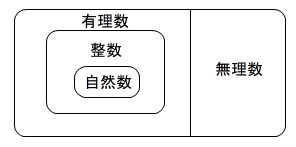
(1)
自然数は整数でもあり有理数でもありますが、
図のどこに入るか最も適切なものを選ぶので限定します。
\(\,①\,\) \(\,5\,\) ：自然数 \(\,\underline{ ウ }\,\)
\(\,②\,\) \(\,\sqrt{3}\,\) ：無理数 \(\,\underline{ エ }\,\)
\(\,③\,\) \(\,\displaystyle \frac{3}{11}\,\) ：有理数 \(\,\underline{ ア }\,\)
数の分類には定義がありますので覚えておきましょう。
(2)
正しいものを選びますが１つでもダメなもの（反例）を探すと早いです。
ア：自然数の逆数\(\displaystyle \,\frac{1}{2}\,\)は自然数ではありません。×
イ：大きい整数を\(\,a\,\)、小さい整数を\(\,b\,\)とすると
\(\hspace{10pt}\displaystyle a-b\,＞\,0\)
は必ず成り立ちます。
整数と整数の差は整数であることは成り立つので自然数ですね。○
ウ：例えば、\(\,(x-1)(x-2)=0\,\)は２次方程式ですが、
解は整数で、無理数ではありません。×
エ：有理数と無理数は実在する数値なので数直線上で表せます。○
無理数は無限に続く小数ですが、
無限に小さく見ていけば点が存在することになります。
（点には大きさがないというのが数学での「点」なので矛盾はしていません。）
例えば\(\,\sqrt{2}=1.4142\cdots\,\)となります。
大きく見ると\(\,1.4\,\)と\(\,1.5\,\)の間に必ず存在するはずです。
第３問円周角の定理の逆
\(\,\large{3}\,\)
円周角の定理の逆についての問題です。
円周角の定理の逆をざっくりいうと、
円周角の定理は、
「同一または同一長の弧または弦に対する円周角が等しくなる。」
ということですが、
逆に４点で作る円周角らしき角が等しくなるとき、
４点が同一円周上にあるというものです。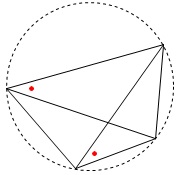
(1)
空欄に適することばは、
「同一円周上にある。」
また
「１つの円周上にある。」
で良いです。
(2)
(1)から\(\,\mathrm{∠CAD=∠CBD}\,\)であるとき、
（４点\(\,\mathrm{A\,,\,B\,,\,C\,,\,D}\,\)が同一円周上にあるとき）
\(\,\mathrm{∠AEB}\,\)の大きさを求めます。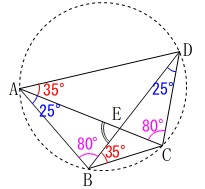
円周角が等しくなるところを書き込むと、
全ての角が定まりますね。
三角形の内角の和から求めれば良いです。
答え \(\,\mathrm{∠AEB}=\underline{ 75^{\circ} }\,\)
\(\,\large{3}\,\)は以上です。
第４問合同の証明と作図
\(\,\large{4}\,\)
図形問題で作図に関する基本です。
(1)
角の二等分線を引く手順が書かれていますが、
手順通りに引くとなぜ角の二等分線になる理由を説明します。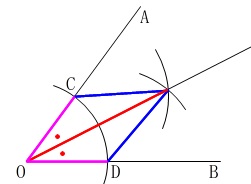
合同の証明ですね。
「３組の辺がそれぞれ等しい。」
が合同条件になります。
証明は省略しますので、
残り２つの条件を書き出してみてください。
(2)
作図問題です。
会員の方は作図の考え方の過程ポイントを、
作図問題集『さくっと！』で確認しておいてください。
先ずは図\(\,\mathrm{Ⅲ}\,\)の折り目\(\,\mathrm{XY}\,\)の説明をしておきます。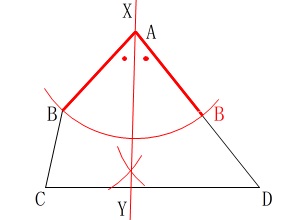
線分\(\,\mathrm{AB}\,\)を\(\,\mathrm{AD}\,\)に重なるように折るということは、
点\(\,\mathrm{A}\,\)は固定なので\(\,\mathrm{B}\,\)を\(\,\mathrm{AD}\,\)上に移動させることになるので、
\(\,\mathrm{∠BAD}\,\)の角の二等分線が折り目になれば良いのです。
（垂線ではないので間違えないようにしましょう。）
図\(\,\mathrm{Ⅱ}\,\)においては、
線分\(\,\mathrm{BC}\,\)が\(\,\mathrm{AD}\,\)上に重なるように折るので、
単なる角の二等分線では\(\,\mathrm{C}\,\)がどこに移動するか分かりません。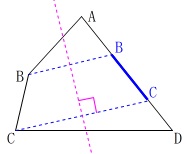
ざっくりとイメージすると折り目（軸）が直線\(\,\mathrm{AD}\,\)と直線\(\,\mathrm{BC}\,\)の、
交点における角の二等分線になれば良いですね。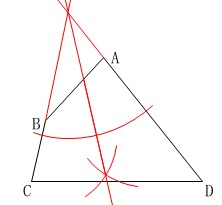
延長線は直線\(\,\mathrm{AD}\,\)と直線\(\,\mathrm{BD}\,\)の交点で切る必要はありませんよ。
（ちょうどとめる方が難しい。）
直線（線分）を延長するのも作図の１つです。
第５問規則性の問題
\(\,\large{5}\,\)
規則性の問題です。
数学の問題解決の基本になることなので、
いくつか試していくと良いですよ。
(1)
４番目の正方形は外側に８個の玉が並びます。
（書き出して見ることをおすすめします。）
計算方法は好きにしていいですが、
（数え上げても良いです。）
正方形や正多角形の場合対称性を見つけて、
縦８つ、横６つとみるよりも４つの組に分けた方が楽です。
外側の白い石は
\(\hspace{10pt}4\times 7\,=\,\underline{ 28 }(個)\)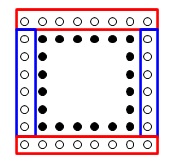
もちろんですが、
\(\hspace{10pt}2\times \color{red}{8}+2\times \color{blue}{6}=\underline{ 28 }\)
でも良いです。
(2)
今度は一般的に外側の石の個数を求めます。
白か黒かは関係ありません。
数遊びとして外側に並ぶ石の個数の規則性を見えると
\(\begin{array}{|c|c|c|c|c|c|} \hline
番目 & 1 & 2 & 3 & 4 & \cdots \\ \hline
個数 & 4 & 12 & 20 & 28 & \cdots \\ \hline
\end{array}\)
８個ずつ増えているのが分かります。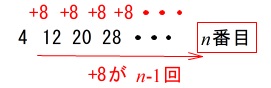
\(\,n\,\)番目までは\(\,n-1\,\)回\(\,8\,\)が増えるので
\(\hspace{10pt}4+8\times (n-1)\\
=\underline{ 8\,n-4 }(個)\)
これを先ほどの対称性から4つに分けるとすると
\(\begin{array}{|c|c|c|c|c|c|} \hline
番目 & 1 & 2 & 3 & 4 & \cdots \\ \hline
個数 & 4\times 1 & 4\times 3 & 4\times 5 & 4\times 7 & \cdots \\ \hline
\end{array}\)
４組の外側の石は奇数の増え方をしているので、
\(\hspace{10pt}4\times (2n-1)\\
=\underline{ 8n-4 }\)
考え方は他にもあります。
例えば、
\(\,n\,\)番目の１辺は偶数\(\,2n\,\)で、
正方形全部を埋めると\(\,(2n)^2\,\)個あり、
中の石を取り除くと考えると、
１つ前の偶数\(\,(2n-2)\,\)の平方を取り除きます。
\(\hspace{10pt}(2n)^2-(2n-2)^2\\
=4n^2-(4n^2-8n+4)\\
=\underline{ 8n-4 }\)
また、単に奇数の列が４組あるので
\(\hspace{10pt}\underline{ 4\,(\,2\,n-1\,) }\)
でも良いですね。
どれでも良いです。
数学の答えは１つでも考え方はそれぞれ違って構いません。
(3)
今度は白黒が関係します。
白と黒がそれぞれ\(\,300\,\)個あります。
\(\,①\,\)
ちょうど使い切るとき
\(\begin{eqnarray}\displaystyle
8n-4&=&300\\
8n&=&304\\
n&=&38
\end{eqnarray}\)
答え \(\,\underline{ 38\,番目 }\,\)
\(\,②\,\)
黒が奇数番目、白が偶数番目に並ぶので、
\(\,n\,\)が偶数だから白を使い切ったことになります。
このとき黒は内側で使う石は\(\,8\,\)個少ないので残りは
\(\hspace{10pt}\underline{ 黒 8\,個 }\)
\(\,37\,\)番目は黒で
\(\hspace{10pt}8\times 37-4\,=292\)
これから残り\(\,8\,\)個としても構いません。
最初に\(\,8\,\)個ずつ増えると考えていたので計算しなかっただけです。
第６問平面図形の動点問題
\(\,\large{6}\,\)
動点問題です。
問題文から条件を読み取りましょう。
正方形\(\,\mathrm{ABCD}\,\)の１辺は\(\,\color{red}{8}\,\)
点\(\,\mathrm{F}\,\)および点\(\,\mathrm{I}\,\)は\(\,\mathrm{AB\,,\,DC}\,\)の中点
\(\,\mathrm{AG=HD=BE=JC=\color{red}{3}}\,\)
点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)の速さで、
\(\,\mathrm{E\rightarrow F\rightarrow G\rightarrow H\rightarrow I\rightarrow J}\,\)の順に動く。
点\(\,\mathrm{P}\,\)が動き出して\(\,x\,\)秒後の\(\,\mathrm{△EJP}\,\)の面積を\(\,y\,\)とする。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。
条件を図の中で見ていきますますが、
三平方の定理から
\(\hspace{10pt}\mathrm{EF=FG=HI=IJ=\color{red}{5}}\,\)
また、正方形の１辺と\(\,\mathrm{AG=HD=3}\,\)から
\(\hspace{10pt}\mathrm{GH=\color{red}{2}}\,\)
であることは確認しておいてください。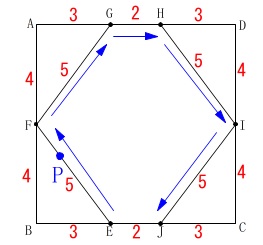
(1)
点\(\,\mathrm{P}\,\)は\(\,\mathrm{E}\,\rightarrow \,\mathrm{J}\,\)まで
\(\hspace{10pt}5+5+2+5+5\,=\,22\)
移動するので
\(\hspace{10pt}\underline{ 22 }秒後\)
(2)
点\(\,\mathrm{P}\,\)が\(\,\mathrm{EF}\,\)上と\(\,\mathrm{HI}\,\)上にあるとき、
\(\,y\,\)を\(\,x\,\)の関数として表します。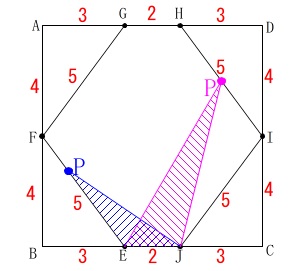
どちらも底辺は\(\,\mathrm{EJ=\color{red}{2}}\,\)の三角形なので、
問題になるのは高さの表し方ですね。
①
点\(\,\mathrm{P}\,\)が辺\(\,\mathrm{EF}\,\)上にあるとき、
\(\,\mathrm{EP}=x\,\)なので\(\,\mathrm{△EJP}\,\)の高さ\(\,\mathrm{PT}\,\)は、
\(\,\mathrm{△EFB}\,\)との相似から、
\(\hspace{4pt}\displaystyle \mathrm{PT}=\color{blue}{\frac{4}{5}\,x}\)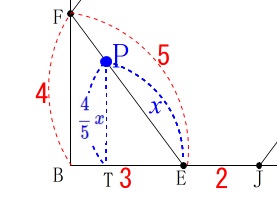
よって、
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \mathrm{EJ}\times \mathrm{PT}\\
&=&\frac{1}{2}\times \color{red}{2}\times \color{blue}{\frac{4}{5}\,x}\\
&=&\frac{4}{5}\,x
\end{eqnarray}\)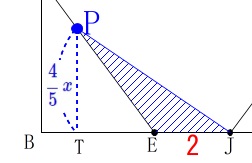
答え \(\hspace{4pt}\displaystyle \underline{ y=\frac{4}{5}\,x }\)
②
点\(\,\mathrm{P}\,\)が辺\(\,\mathrm{HI}\,\)上にあるとき、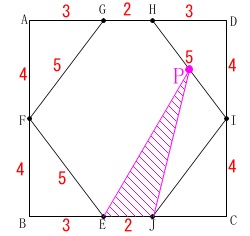
高さ\(\,\mathrm{PT}\,\)は、
正方形の１辺\(\,\color{red}{8}\,\)から垂線\(\,\mathrm{PS}\,\)を引いて求めておきます。
（高さの出し方はいろいろあります。）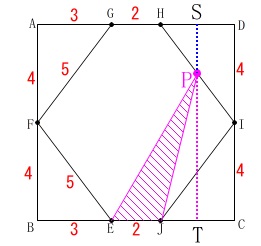
点\(\,\mathrm{P}\,\)は\(\,\mathrm{E}\,\)から\(\,\mathrm{P}\,\)まで\(\,x\,\)動いていて、
\(\,\mathrm{H}\,\)までの長さが\(\,\color{red}{5}+\color{red}{5}+\color{red}{2}\,=\,12\,\)なので
\(\hspace{4pt}\mathrm{PH}=\color{magenta}{x-12}\)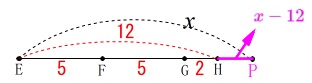
動点の部分的な長さは直線上の移動に置き換えると分かり易いですよ。
このとき\(\,\mathrm{PS}\,\)の長さは\(\,①\,\)と同じように相似から
\(\hspace{4pt}\displaystyle \mathrm{PS}=\color{blue}{\frac{4}{5}\,(x-12)}\)
となるので\(\,\mathrm{△EJP}\,\)の高さ\(\,\mathrm{PT}\,\)は
\(\begin{eqnarray}\displaystyle
\mathrm{PT}&=&\color{red}{8}-\color{blue}{\frac{4}{5}\,(12-x)}\\
&=&\color{magenta}{\frac{88}{5}-\frac{4}{5}\,x}
\end{eqnarray}\)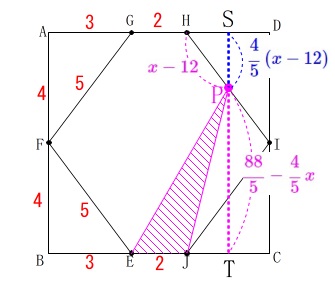
よって、
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \mathrm{EJ}\times \mathrm{PT}\\
&=&\frac{1}{2}\times 2\times \left(\,\frac{88}{5}-\frac{4}{5}\,x\,\right)\\
&=&\frac{88}{5}-\frac{4}{5}\,x\\
&=&\underline{\underline{ \frac{4}{5}\,(\,22-x\,) }}
\end{eqnarray}\)
線分\(\,\mathrm{PI}\,\)の長さを\(\,17-x\,\)として高さを出しても良いですよ。
そのときは
\(\begin{eqnarray}\displaystyle
\mathrm{PT}&=&4+\frac{4}{5}(\,17-x\,)\\
&=&\frac{88}{5}-\frac{4}{5}\,x
\end{eqnarray}\)
と\(\,\mathrm{IC}=\color{red}{4}\,\)を足すことになります。
気がついている人もいると思いますが、
底辺が\(\,2\,\)なので三角形の面積は高さと同じになります。
(3)
点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{P}\,\)の\(\,3\,\)秒後に移動します。
速さは毎秒\(\,2\,\)（\(\,\mathrm{P}\,\)の\(\,2\,\)倍）で動く方向は点\(\,\mathrm{P}\,\)と同じです。
\(\,\mathrm{△EJP}\,\)と\(\,\mathrm{△EJQ}\,\)の面積が等しくなるのは、
点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{P}\,\)に追いつき同じ位置にいるときか、
点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{P}\,\)を追い越し同じ高さになるときです。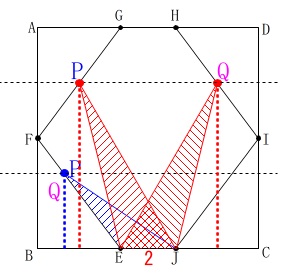
意味が分からないという場合は(2)を見直しておいてください。
※
図の位置は正確ではありません。
直感的に面積が等しいときがイメージできていれば良いです。
このときの点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)の移動する長さを表しておくと
点\(\,\mathrm{P}\,\)：\(\hspace{4pt}\color{red}{x}\)
点\(\,\mathrm{Q}\,\)：\(\hspace{4pt}\color{blue}{2(x-3)}\)
詳しく説明することもないでしょう。
早速答えを出します。
点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{P}\,\)に追いつくのは、
移動した距離が同じになるときなので
\(\begin{eqnarray}\displaystyle
x&=&2(x-3)\\
x&=&6
\end{eqnarray}\)
このとき点\(\,\mathrm{P\,,\,Q}\,\)は線分\(\,\mathrm{FG}\,\)上にあり重なっています。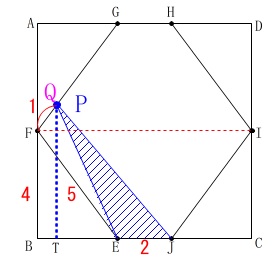
点\(\,\mathrm{F}\,\)で折り返してくるのでわかりにくいですが、
線分\(\,\mathrm{FG}\,\)上にいるときも高さは移動に比例して大きくなります。
折り返すのではなくそのまま進むと考えると分かり易いですね。
このときの面積を表す関数は\(\,\mathrm{EF}\,\)上にあるときと同じで
\(\hspace{4pt}\displaystyle y=\frac{4}{5}\,x\)
よって、\(\,x=6\,\)のとき
\(\begin{eqnarray}\displaystyle
y&=&\frac{4}{5}\times 6\\
&=&\frac{24}{5}
\end{eqnarray}\)
具体的に高さを出す場合、
\(\begin{eqnarray}\displaystyle
\mathrm{PT}&=&\color{magenta}{\frac{4}{5}}+\color{red}{4}\\
&=&\frac{24}{5}
\end{eqnarray}\)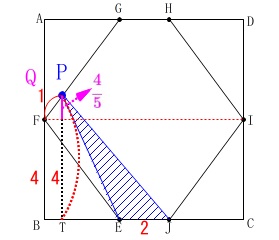
よって、
面積は\(\displaystyle \,y=\frac{24}{5}\,\)となります。
どちらでも良いです。
次に追い越した後同じ高さになるときは、
線分\(\,\mathrm{EF+FP}\,\)と線分\(\,\mathrm{JI+IQ}\,\)が同じになるときです。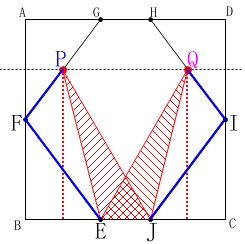
点\(\,\mathrm{P}\,\)の移動は\(\,x\,\)そのままで良いので
\(\hspace{4pt}\mathrm{EF+FP}=\color{blue}{x}\,\)
線分\(\,\mathrm{JI+IQ}\,\)は\(\,\mathrm{E}\,\)から\(\,\mathrm{J}\,\)まで移動したときの\(\,\color{red}{22}\,\)から、
点\(\,\mathrm{Q}\,\)の移動\(\,\color{magenta}{2(x-3)}\,\)を引けば出てきます。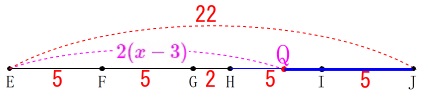
このことから
\(\begin{eqnarray}\displaystyle
\mathrm{EF+FP}&=&\mathrm{JI+IQ}\\
\color{blue}{x}&=&\color{red}{22}-\color{magenta}{2(x-3)}\\
3x&=&28\\
x&=&\frac{28}{3}
\end{eqnarray}\)
このとき点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{FG}\,\)上にあります。
面積は\(\,\mathrm{△EJP}\,\)と等しいので、
\(\begin{eqnarray}\displaystyle
y&=&\frac{4}{5}\times \frac{28}{3}\\
&=&\frac{112}{15}
\end{eqnarray}\)
答え
\(\hspace{4pt}\displaystyle \underline{\underline{ x=6\,のとき\,y=\frac{24}{5} }}\)
または
\(\hspace{4pt}\displaystyle \underline{\underline{ x=\frac{28}{3}\,のとき\,y=\frac{112}{15} }}\)
要点だけをまとめましたが、
\(\hspace{4pt}0\,≦\,x\,≦\,5\,\)
\(\hspace{4pt}5\,≦\,x\,≦\,10\,\)
\(\hspace{4pt}10\,≦\,x\,≦\,12\)
\(\hspace{4pt}12\,≦\,x\,≦\,17\)
\(\hspace{4pt}17\,≦\,x\,≦\,22\)
と分けて全ての場合考えると抜け落ちは無くなります。
ただ、
点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)が線分\(\,\mathrm{GH}\,\)上に同時にあることはない、
とだけ確認しておけばこの問題に関しては良いでしょう。
考え方は１つではないので、
違った考えで答えを出した人も間違いではありません。
基本中心である程度の作業を手を止めることなく進めれば、
全ての時間内で答えまでたどり着けると思います。
基本の徹底を対策にするとよろしいのではないでしょうか。
以上です。
前期選抜試験はもっと基本的です。
例年ムラのない問題を作ってくれていますので前期の問題にも目を通し、
後期試験の対策としてムラのない基礎を作っておきましょう。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
