2022年(令和4年)度大阪府公立高校入試の数学Ｃ問題と解説

2022年(令和4年)度大阪府公立高校入試の数学Ｃ問題と解説です。
大問３問構成で問題数としては少なく見えますが、
一つひとつが標準以上の問題なので直感的に答えが見えてくる問題は少ないです。
解決の糸口を探すための作業を止めると時間が足りなくなりますよ。

2022年(令和4年)度大阪府公立高校入試の数学Ｃの問題

令和４年度大阪府立高校入試の数学Ｃ問題です。

⇒　２０２２令和４年度大阪府立高校入試の数学Ｃ問題ＰＤＦ

パッと見た目で大問３つは例年通りです。

2022年(令和4年)度大阪府公立高校入試の数学Ｃ問題の解説

例年通りだと標準、応用問題での構成となりますが、
Ｃ問題を選択する時点である程度の基礎はできているものとして、
解説を省略するところもありますのでご了承下さい。
（基本は『覚え太郎』に任せておきます。）
※
Ａ問題Ｂ問題をみておくと基本の確認になりますよ。

応用問題の途中計算は省略することもあるので、
なぜ？と感じたらご自身で手を動かして計算してみて下さい。

それと、たぶん、
全問通じて長さの単位は\(\,\mathrm{cm}\,\)なので全て省略します。
（「問題確認してから書けよ。」といわれそうなので確認しておきました。）

第１問

\(\,\large{1}\,\)
計算、方程式、資料から関数の文字設定まで８題あります。
後半を考えると素早く終わらせたいところですが、
落とすのももったいないので慎重に進めましょう。
(1)
　\(\hspace{10pt}\displaystyle \frac{3a-b}{4}-\frac{a-2b}{6}\\
\displaystyle =\frac{3(3a-b)-2(a-2b)}{12}\\
\displaystyle =\frac{9a-3b-2a+4b}{12}\\
\displaystyle =\underline{\underline{　\frac{7a+b}{12}　}}\)

単なる文字式の分数計算ですが、
分子には（かっこ）がついていることを忘れずに、
展開時の符号に注意です。

(2)
連立方程式です。
教科書にもある形なので問題ないでしょう。
　\(\hspace{4pt}x-16y+10=5x-14=-8y\)

どの組でも良いですがここでは最右辺を２回使います。
　\( \begin{cases}
\hspace{4pt} x-16y+10=-8y\\
\hspace{4pt} 5x-14=-8y
\end{cases}\)
これを解くと、
　\(\hspace{4pt}\displaystyle \underline{\underline{　x=\frac{2}{3}　,　y=\frac{4}{3}　}}\)

(3)
代入問題です。
会員の方は問題ないでしょうが、代入は最後です。

さらにここでは与式（求値式）の変形後にすぐ代入ではなく、
部分的に計算してからの方が楽（見やすい）ですよ。
　\(\hspace{10pt}x^2-y^2\\
=(x+y)(x-y)\)

ここで
　\(\hspace{10pt}x+y=2\sqrt{15}\\
\hspace{10pt}x-y=2\sqrt{5}\)
なので
　\(\begin{eqnarray}\displaystyle
(x+y)(x-y)&=&2\sqrt{15}\times 2\sqrt{5}\\
&=&\underline{　20\sqrt{3}　}
\end{eqnarray}\)

与式が交代式だからですが、
与式や\(\,x\,,\,y\,\)の値がなんとなく対称的になっているなあ、
という感じるだけでも良いです。

(4)
文字の符号を考えます。
　\(\hspace{10pt}ax+by=1\)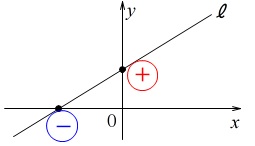切片の符号と傾きが読み取れるので問題ありませんね。

直線が傾きを持っているので\(\,b=0\,\)ではないから、
両辺を\(\,b\,\)で割ることができ
　\(\begin{eqnarray}\displaystyle
ax+by&=&1\\
y&=&-\frac{a}{b}x+\frac{1}{b}
\end{eqnarray}\)
図より\(\,y\,\)切片は正なので
　\(\hspace{10pt}b\,＞\,0\)
また傾きは正なので
　\(\hspace{10pt}\displaystyle -\frac{a}{b}\,＞\,0\)
これと\(\,b\,＞\,0\,\)から
　\(\hspace{10pt}a\,＜\,0\)

答え　\(\,\underline{　ウ　}\,\)

方程式を
　\(\hspace{10pt}\displaystyle \frac{x}{\frac{1}{a}}+\frac{y}{\frac{1}{b}}=1\)
と変形すれば与えられた図の切片から
（\(\,x=0\,,\,y=0\,\)のときを考えて）
　\(\hspace{4pt}\displaystyle (x\,切片\,)=\frac{1}{a}\,＜\,0\)
　\(\hspace{4pt}\displaystyle (y\,切片\,)=\frac{1}{b}\,＞\,0\)
とすることもできます。

(5)
確率です。

条件は問題から読み取っておいて下さい。
「３枚取り出したカードのうち、
　小さい順に\(\,a\,,\,b\,,\,c\,\)とする。」

あれこれ考えず樹形図で良いですよ。
ここでは表で見ておきます。

箱\(\,\mathrm{A}\,\)からの２枚の取り出し方は
　\(\hspace{4pt}\color{red}{(\,2\,,\,4\,)}\,,\,\color{red}{(\,2\,,\,6\,)}\,,\,\color{red}{(\,4\,,\,6\,)}\)
の３通り。
箱\(\,\mathrm{B}\,\)からの１枚の取り出し方は
　\(\hspace{4pt}\color{blue}{1}\,,\,\color{blue}{3}\,,\,\color{blue}{9}\)
３通り。
そのとき\(\,\displaystyle \frac{ac}{b}\,\)が自然数になる確率です。
　\(\begin{array}{|c|c|c|c|} \hline
&　 \color{blue}{1}　 &　 \color{blue}{3}　 &　 \color{blue}{9}　 \\ \hline
　\color{red}{(\,2\,,\,4\,)}　 & ○ & & \\ \hline
　\color{red}{(\,2\,,\,6\,)}　 & ○ & ○ & ○ \\ \hline
　\color{red}{(\,4\,,\,6\,)}　 & & & ○ \\ \hline
\end{array}\)
もう少し樹形図っぽく見やすくしておきましょうか。
　\(\begin{array}{|c|c|c|c|} \hline
　取り出した３枚　 &　 ac　 &　 b　 &　\displaystyle \frac{ac}{b} 　 \\ \hline
　\color{red}{(\,2\,,\,4\,)}－\color{blue}{1}　 & 4 & 2 & ○ \\ \hline
　\color{red}{(\,2\,,\,4\,)}－\color{blue}{3}　 & 8 & 3 & \\ \hline
　\color{red}{(\,2\,,\,4\,)}－\color{blue}{9}　 & 18 & 4 & \\ \hline
　\color{red}{(\,2\,,\,6\,)}－\color{blue}{1}　 & 6 & 2 & ○ \\ \hline
　\color{red}{(\,2\,,\,6\,)}－\color{blue}{3}　 & 12 & 3 & ○ \\ \hline
　\color{red}{(\,2\,,\,6\,)}－\color{blue}{9}　 & 18 & 6 & ○ \\ \hline
　\color{red}{(\,4\,,\,6\,)}－\color{blue}{1}　 & 6 & 4 & \\ \hline
　\color{red}{(\,4\,,\,6\,)}－\color{blue}{3}　 & 18 & 4 & \\ \hline
　\color{red}{(\,4\,,\,6\,)}－\color{blue}{9}　 & 36 & 6 & ○ \\ \hline
\end{array}\)
３枚のうち\(\,b\,\)に着目すれば分かり易いでしょう。
樹形図では\(\,b\,\)となる数字に\(\,○\,\)でも付ければ見やすいです。
　\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{5}{9}　}}\)

ポイントは、
確率を求める公式があると思わないことです。
「場合」を考えることが確率の基本ですよ。

(6)
度数と相対度数の問題です。

サッカー部の度数を\(\,a\,\)とすると
バレーボール部の度数は\(\,a-3\,\)とおけて、
相対度数が同じなので
　\(\begin{eqnarray}\displaystyle
\frac{a}{32}&=&\frac{a-3}{20}\\
20\,a&=&32\,(a-3)\\
a&=&\underline{　8　}
\end{eqnarray}\)

(7)
文字式の扱いです。

２けたの自然数の十の位を\(\,a\,\)、一の位を\(\,b\,\)とすると
　\(\hspace{10pt}m=10\,a+b\)
　\(\hspace{10pt}n=a+b\)
とおけるので
　\(\hspace{10pt}11\,n-2\,m\\
=11(a+b)-2(10a+b)\\
=9b-9a\\
=9(b-a)　･･･①\)
これが\(\,50\,\)以上、\(\,60\,\)以下となるのは
（\(\,a\,,\,b\,\)が自然数であることを考えて）
　\(\hspace{10pt}b-a=6\)
のときしかありません。
（当然\(\,b\,＞\,a\,\)）
\(\,b\,\)が大きい方から探して
　\(\hspace{4pt}(\,b=9\,,\,a=3\,)\,,\,(\,b=8\,,\,a=2\,)\,,\,(a=7\,,\,b=1\,)\)
よって
　\(\hspace{10pt}\underline{　17\,,\,28\,,\,39　}\)

\(\begin{eqnarray}\displaystyle
50\,≦&\,9(b-a)\,&≦\,60\\
\frac{50}{9}≦&b-a&≦\frac{60}{9}\\
5.\cdots≦&b-a&≦6.\cdots
\end{eqnarray}\)
としても良いですが、メンドウでしょう？
　\(\hspace{4pt}b-a=5\,\)のときダメ
　\(\hspace{4pt}b-a=7\,\)のときダメ
と検討をつければ\(\,b-a=6\,\)と固定されます。

\(\,m\,\)は自然数でも\(\,b\,\)は\(\,0\,\)でも良いのでは？
と考えた人は注意深いですね。
ですが\(\,①\,\)の満たす条件から\(\,b=0\,\)はあり得ません。

(8)
関数の文字設定です。

問題文の条件は読み取っておいて下さい。

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると、（\(\,t\,＞\,0\,\)）
　\(\,\mathrm{A}\,\)：\(\,\displaystyle \left(\,t\,,\,\,\frac{1}{3}\,t^2\,\right)\)
点\(\,\mathrm{B}\,\)は関数が\(\,y\,\)軸対称なので
　\(\,\mathrm{B}\,\)：\(\,\displaystyle \left(\,-t\,,\,\,\frac{1}{3}\,t^2\,\right)\)
点\(\,\mathrm{C}\,\)は\(\,\mathrm{A\,,\,B}\,\)と\(\,y\,\)座標は同じ\(\,y\,\)軸上の点なので
　\(\,\mathrm{C}\,\)：\(\,\displaystyle \left(\,0\,,\,\,\frac{1}{3}\,t^2\,\right)\)
点\(\,\mathrm{E}\,\)は\(\,\mathrm{CE=4}\,\)となる\(\,y\,\)軸上の点なので
　\(\,\mathrm{E}\,\)：\(\,\displaystyle \left(\,0\,,\,\,\frac{1}{3}\,t^2-4\,\right)\)

ここからは方向性が別れると思います。
直線上の点\(\,\mathrm{D}\,\)を先に設定するか、
条件から点\(\,\mathrm{D}\,\)を\(\,t\,\)で表し直線上にあるとするかです。
どっちでも良いです。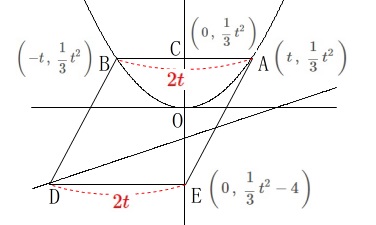平行四辺形\(\,\mathrm{ABDC}\,\)の条件から点\(\,\mathrm{D}\,\)の座標は、
点\(\,\mathrm{E}\,\)より\(\,\color{red}{2t}\,\)だけ左に移動するので
　\(\,\mathrm{D}\,\)：\(\,\displaystyle \color{red}{\left(\,-2t\,,\,\,\frac{1}{3}\,t^2-4\,\right)}\)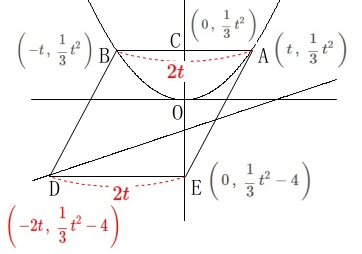これが直線\(\,\ell\,\)上にあることから
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{1}{3}\,t^2-4}&=&\frac{1}{3}\,(\,\color{red}{-2t}\,)-1\\
t^2-12&=&-2t-3\\
t^2+2t-9&=&0\\
t&=&-1\pm \sqrt{10}
\end{eqnarray}\)
条件から
　\(\hspace{10pt}t=\underline{　-1+\sqrt{10}　}\)

点\(\,\mathrm{D}\,\)の\(\,x\,\)座標が\(\,-2t\,\)となるので、
直線\(\,\ell\,\)上の点だから
　\(\,\mathrm{D}\,\)：\(\displaystyle \,\left(\,-2t\,,\,\frac{1}{3}(\,-2t\,)-1\right)\,\)
この\(\,y\,\)座標が\(\,\mathrm{C}\,\)と同じなので
　\(\begin{eqnarray}\displaystyle
\frac{1}{3}(\,-2t\,)-1&=&\frac{1}{3}\,t^2-4\\
-2t-3&=&t^2-12\\
t^2+2t-9&=&0
\end{eqnarray}\)
としても結果は同じです。

問題の条件を活かせばどっちでも良いです。

第２問

みたまま平面図形ですので、
条件を図の中で整理しながら簡単に済ませす。

とりあえず\(\,\mathrm{C}\,\)と\(\,\mathrm{F}\,\)を結びたくなるでしょう。笑
（弧でみても良いですけど。）
\(\,\mathrm{△DEC}\,\)が直角二等辺三角形なので底角が\(\,45°\,\)です。
弦\(\,\mathrm{CF}\,\)の円周角が\(\,45°\,\)なので中心角が\(\,90°\,\)になるので
　\(\hspace{4pt}\mathrm{∠COG}=90^{\circ}\)
問題からの読み取りはこれくらいにして先に進みましょう。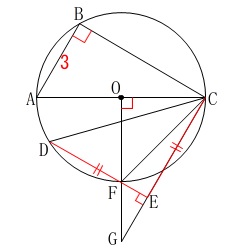点\(\,\mathrm{O}\,\)が円の中心であることは説明の必要もないでしょう。

(1)
円の面積を求めます。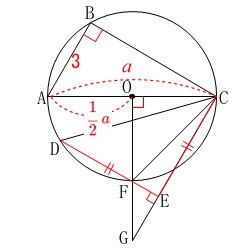辺\(\,\mathrm{AC}\,\)は円の直径なので半径が\(\displaystyle \,\color{red}{\frac{1}{2}\,a}\,\)だから
　\(\hspace{10pt}\displaystyle \pi\times \left(\frac{1}{2}\,a\right)\\
\displaystyle =\underline{\underline{　\frac{1}{4}\,\pi\,a^2　}}(\,\mathrm{cm^2}\,)\)

辺\(\,\mathrm{AC}\,\)が円の直径であることは\(\,\mathrm{∠ABC}\,\)から分かりますが、
\(\,\mathrm{∠COG}\,\)が\(\,90°\,\)ということは、
条件がなければ問題の図からだけでは判断できません。

(2)
相似の証明です。

平行線の錯角が等しくなる事から、
図の中で終わっていますので省略します。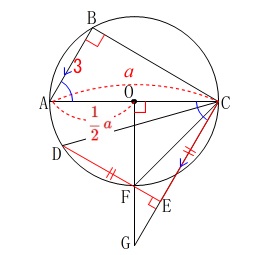相似条件は
　「２組の角がそれぞれ等しい。」
です。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△COG}\,\)

この証明までの流れが理解できない場合は『覚え太郎』から始めましょう。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明の書き方は自分のやりやすい形で良いですよ。

(3)
ここからが\(\,\large{2}\,\)の本番です。

具体的な長さがさらに与えられます。
　\(\hspace{4pt}\mathrm{BC}=\color{blue}{5}\)

三平方の定理から
　\(\hspace{10pt}\mathrm{AC}=\color{magenta}{\sqrt{34}}\)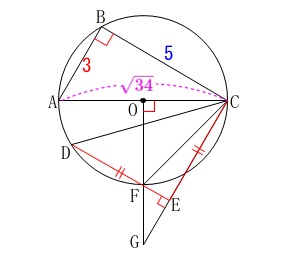このとき半径は
　\(\hspace{4pt}\displaystyle \mathrm{AO=OC}=\color{red}{\frac{\sqrt{34}}{2}}\)
①
線分\(\,\mathrm{OG}\,\)の長さを求めます。
(2)で証明した相似を使いましょう。
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△COG}\,\)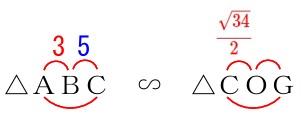　\(\begin{eqnarray}\displaystyle
\mathrm{AB:BC}&=&\mathrm{CO:OG}\\
3:5&=&\frac{\sqrt{34}}{2}:\mathrm{OG}\\
\mathrm{OG}&=&\underline{\underline{　\frac{5}{6}\sqrt{34}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

出てきた長さを図に書き込みます。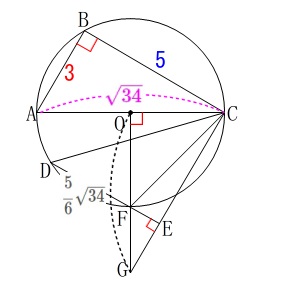問題によって使うかどうかはわかりませんが、
次の問題のヒントとしてくれていることが多いです。

②
四角形\(\,\mathrm{OFEC}\,\)の面積です。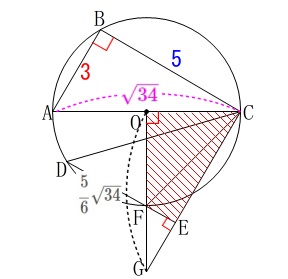半径\(\,\mathrm{OC}\,\)の長さがが分かっているので、
\(\,\mathrm{△GOC}\,\)の面積が分かるからそこから出そうです。
　\(\begin{eqnarray}\displaystyle
\mathrm{△GOC}&=&\frac{1}{2}\times \mathrm{OC}\times \mathrm{OG}\\
&=&\frac{1}{2}\times \frac{\sqrt{34}}{2}\times \frac{5}{6}\sqrt{34}\\
&=&\frac{17\times 5}{12}
\end{eqnarray}\)

相似を利用する方向で良いですが、
公式のない面積なので（あるにはあるけど）
　『部分』＋『部分』
または
　『全体』－『部分』
で求めるのが普通ですね。

いくつか方法があるので別解を連ねても良いですが、
相似を使って１つだけ説明しておきます。

ゴチャゴチャしているので\(\,\mathrm{△GOC}\,\)を抜き出して説明します。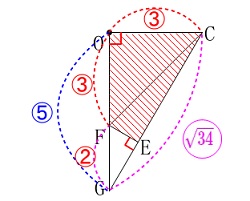表しているのは比です。

相似をみたときの比から\(\,\mathrm{OC:OG}=\color{red}{3}:\color{blue}{5}\,\)で、
半径から\(\,\mathrm{OC=OF}\,\)だから
　\(\hspace{4pt}\mathrm{OF:FG}=\color{red}{3}:\color{red}{2}\)
三平方の定理でも良いですが\(\,\mathrm{CG}=\color{magenta}{\sqrt{34}}\,\)なので、
　\(\,\mathrm{△GOC}\,\)　∽　\(\,\mathrm{△GEF}\,\)
における相似比が
　\(\hspace{4pt}\mathrm{GC:GF}=\color{magenta}{\sqrt{34}}:\color{red}{2}\)
このとき面積比が
　\(\hspace{4pt}\mathrm{△GOC:△GEF}=34:4\)
このことから\(\,\mathrm{△GDF}\,\)を引いて考えると
　\(\hspace{4pt}\mathrm{△GOC}:(\,四角形\,\mathrm{OFEC}\,)=34：30=17:15\)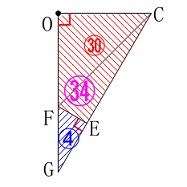よって、四角形\(\,\mathrm{OFEC}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{15}{17}\times \mathrm{△GOC}\\
&=&\frac{15}{17}\times \frac{17\times 5}{12}\\
&=&\underline{\underline{　\frac{25}{4}　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)
　
線分の長さは全て求められる設定なので求めても良いですよ。
（線分\(\,\mathrm{CG}\,\)の長さが割ときれいな数字で出るので）
その場合は\(\,\mathrm{△GOC}\,\)から\(\,\mathrm{△GEF}\,\)を引く方法が単純に出ます。

第３問

立体図形の問題です。

問題の条件を簡単にまとめると、
図\(\,\mathrm{Ⅰ}\,\)の立体は三角柱を平面で切った図形で、
図\(\,\mathrm{Ⅱ}\,\)の体積を求める部分は
図\(\,\mathrm{Ⅰ}\,\)の立体を平面で切った図形です。
（直感的にとらえたままで大丈夫です。）

(1)
長さが与えられているので図の中で確認しておきましょう。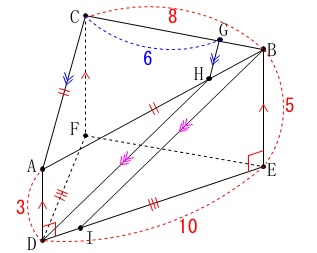早速問題に取りかかります。

言っておきますが、（『覚え太郎』会員にはクドくなるけど）
立体は平面の組合わせでできています。
①
\(\,\mathrm{△DEF}\,\)の面積です。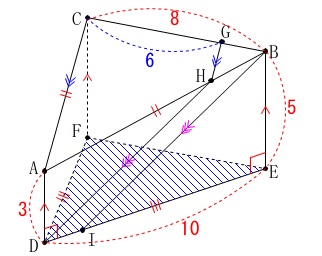単に二等辺三角形の面積を求めよ、といっています。

高さ（下図の\(\,\mathrm{DM}\,\)）が欲しい。
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{DM^2}&=&\mathrm{DF^2-FM^2}\\
&=&10^2-4^2\\
&=&84\\
\mathrm{DM}&=&\color{blue}{2\sqrt{21}}\,(\,＞\,0\,)
\end{eqnarray}\)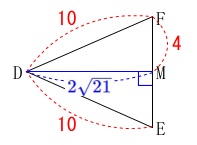よって
　\(\begin{eqnarray}\displaystyle
\mathrm{△DEF}&=&\frac{1}{2}\times \mathrm{FE}\times \mathrm{DM}\\
&=&\frac{1}{2}\times 8\times \times 2\sqrt{21}\\
&=&\underline{　8\sqrt{21}　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

次いきます。

②
線分\(\,\mathrm{HB}\,\)の長さを求めます。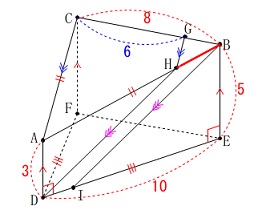\(\,\mathrm{△ABC}\,\)の面の相似から
　\(\begin{eqnarray}\displaystyle
\mathrm{AH:HB}&=&\mathrm{CG:GB}\\
&=&6:2\\
&=&3:1
\end{eqnarray}\)
つまり\(\,\mathrm{HB}\,\)の長さは線分\(\,\mathrm{AB}\,\)の\(\displaystyle \,\color{red}{\frac{1}{4}}\,\)です。

線分\(\,\mathrm{AB}\,\)の長さが分かっていないのでみる方向を変えます。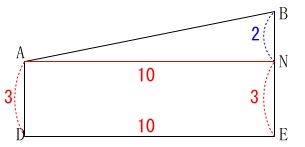台形\(\,\mathrm{ADEB}\,\)において\(\,\mathrm{A}\,\)から\(\,\mathrm{BE}\,\)に垂線を引くと、
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2}&=&\mathrm{AN^2+BN^2}\\
&=&10^2+2^2\\
&=&104\\
\mathrm{AB}&=&\color{magenta}{2\sqrt{26}}\,(\,＞\,)
\end{eqnarray}\)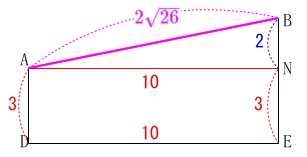よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{HB}&=&\frac{1}{4}\times \mathrm{AB}\\
&=&\color{red}{\frac{1}{4}}\times \color{magenta}{2\sqrt{26}}\\
&=&\underline{\underline{　\frac{\sqrt{26}}{2}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

③
今度は線分\(\,\mathrm{DI}\,\)です。

普通に\(\,\mathrm{AD}\,,\,\mathrm{BI}\,\)を延長して相似でも良さそうですが、
（そろそろ飽きてきた頃だと思うので）
出てきた相似と文字を使って方程式にしましょう。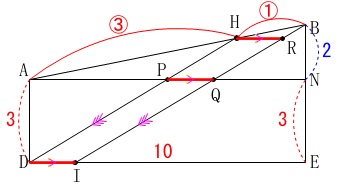図において３つの平行線を考えて
　\(\hspace{4pt}\mathrm{DI=PQ=HR}=\color{red}{x}\)
とします。
　\(\hspace{4pt}\mathrm{AH:HB=AP:HR}=3:1\)
なので
　\(\hspace{4pt}\mathrm{AP}=\color{blue}{3x}\)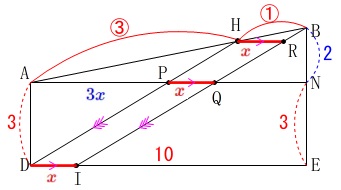また
　\(\hspace{4pt}\mathrm{IE=DE-DI}=10-x\)
となるので\(\,\mathrm{BN}\,\)と\(\,\mathrm{NE}\,\)の比から
　\(\begin{eqnarray}\displaystyle
\mathrm{QN}&=&\frac{2}{5}\times \mathrm{IE}\\
&=&\color{magenta}{\frac{2}{5}\,(\,10-x\,)}
\end{eqnarray}\)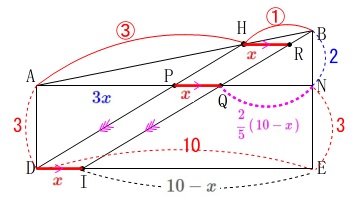線分\(\,\mathrm{AN}\,\)は\(\,\mathrm{DE}\,\)と等しく\(\,\color{red}{10}\,\)なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{3x}+\color{red}{x}+\color{magenta}{\frac{2}{5}(10-x)}&=&\color{red}{10}\\
x&=&\underline{\underline{　\frac{5}{3}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

延長線や平行線を補助線として引けば相似だらけなので、
自分で方針を立てたら突っ走ってみると良いです。

(2)
図\(\,\mathrm{Ⅱ}\,\)における長さと体積です。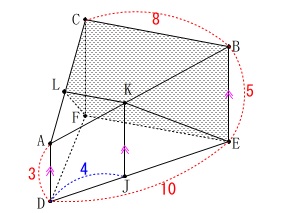①
線分\(\,\mathrm{LK}\,\)の長さを求めます。

条件から
　\(\,\mathrm{DJ=\color{blue}{4}}\,\)なので\(\hspace{4pt}\mathrm{JE}=\color{blue}{6}\)
また
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{KJ}\,\)∥\(\,\mathrm{BE}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AK:KB}&=&\mathrm{DJ:JE}\\
&=&\color{blue}{4}:\color{blue}{6}\\
&=&\color{magenta}{②}:\color{magenta}{③}
\end{eqnarray}\)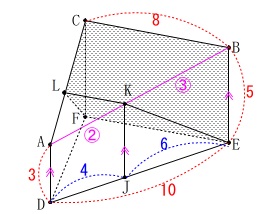このことから\(\,\mathrm{△ABC}\,\)をながめると
　\(\begin{eqnarray}\displaystyle
\mathrm{LK}&=&\frac{2}{2+3}\times \mathrm{BC}\\
&=&\frac{2}{5}\times \color{red}{8}\\
&=&\underline{\underline{　\frac{16}{5}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

③
斜線部分の体積を求めます。

あれこれ考えても出てくる体積は同じなので、
簡単に説明しておきます。

公式の使えない体積なので『部分』に分けて、合わせましょう。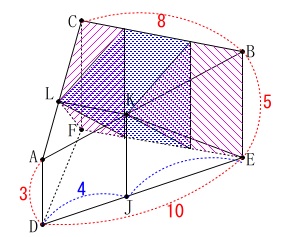両脇の２つの四角錐と間にある１つの三角柱に分けます。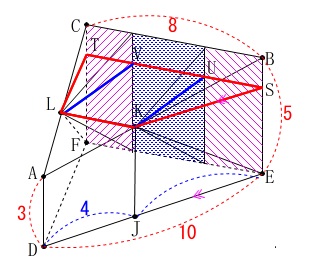面\(\,\mathrm{DEF}\,\)は面\(\,\mathrm{CFEB}\,\)に垂直になっているので、
\(\,\mathrm{LK}\,\)を含む平面のうち、
\(\,\mathrm{△DEF}\,\)に平行な面で切ると面\(\,\mathrm{CFEB}\,\)に垂直になります。
（図の赤線で囲んだ四角形を含む平面です。）

四角錐の高さは\(\,\mathrm{\color{blue}{KU}}\,\)または\(\,\mathrm{\color{blue}{LV}}\,\)が使えます。
さらに三角柱の底面の三角形の高さでもあります。

四角形\(\,\mathrm{LKST}\,\)を抜き出して、
等脚台形なので辺や垂線の長さや面積を求めていきましょう。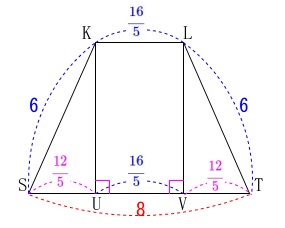三平方の定理から
　\(\hspace{4pt}\displaystyle \mathrm{KU=LV}=\color{red}{\frac{6\sqrt{21}}{5}}\)
となり、これが四角錐と三角柱の底面の三角形の高さです。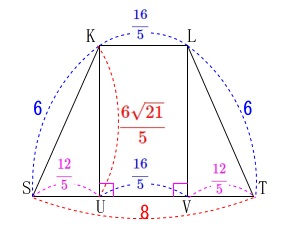では、立体の体積を求めに行きましょう。
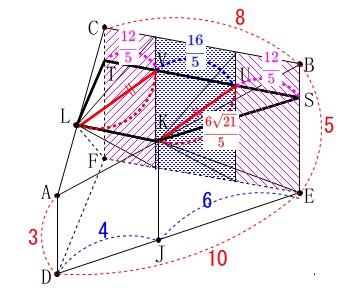どちらからでも良いですが、
中にある三角柱の体積\(\,V_1\,\)は、
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{2}\times \color{red}{5}\times \color{red}{\frac{6\sqrt{21}}{5}}\times \color{blue}{\frac{16}{5}}\\
&=&\frac{48\sqrt{21}}{5}
\end{eqnarray}\)

両脇にある四角錐は同じ体積なので２つ分の体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&2\times \frac{1}{3}\times \color{magenta}{\frac{12}{5}}\times \color{red}{5}\times \color{red}{\frac{6\sqrt{21}}{5}}\\
&=&\frac{48\sqrt{21}}{5}
\end{eqnarray}\)

よって求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&V_1+V_2\\
&=&\frac{48\sqrt{21}}{5}+\frac{48\sqrt{21}}{5}\\
&=&\underline{\underline{　\frac{96\sqrt{21}}{5}　}}\,(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

途中計算をかなり省略していますが、
Ｃ問題では普通なのでやってみて下さい。
それほど手強い計算ではありません。

解説が手抜き？
いやいやこれを計算できなければ、
今はＣ問題にはチャレンジしない方が良いです。
『覚え太郎』と『基本レポート』からやり直しましょう。

以上です。

⇒　2022年(令和4年)度大阪府公立高校入試の数学Ｂ問題と解説

Ｂ問題はＣ問題にステップアップするためには必須の基本です。
もちろんＡ問題は制限時間の半分で済ませられるようになってからです。
『覚え太郎』＋『基本レポート』で十分ですので余計な事は考えず専念してみて下さい。

⇒　大阪府公立高校入試数学の過去問と解答解説

大阪府立入試では作図が出ませんが、（今のところ）
全般の基本はもちろんですが、
図形の基本性質はレベルを上げて抑えておくと良いですね。