2022年(令和4年)度大阪府公立高校入試の数学Ｂ問題と解説

2022年(令和4年)度大阪府公立高校入試の数学Ｂ問題と解説です。
基本と標準の大問４つの問題構成で問題文の説明が詳しいので長く見えますが、
内容は非常にシンプルにできています。
ここは対策ページではありませんが基本を徹底的に抑えておけば十分対応できるでしょう。

2022年(令和4年)度大阪府公立高校入試の数学Ｂの問題

令和４年度大阪府立高校入試のＢ問題です。

⇒　2022年(令和4年)度大阪府公立高校入試の数学Ｂ問題ＰＤＦ

Ａ問題では解答用紙を省きましたが、
Ｂ問題では解答用紙も添えておきました。

2022年(令和4年)度大阪府公立高校入試の数学Ｂ問題の解説

大問４問は例年と変わらず、
基本から標準レベルでの構成も例年通りです。

Ｂ問題も『覚え太郎』までで十分満点を狙えますが、
『超え太郎』で少し楽をする方法も加えて解説していってみます。
逆に、規則性を利用して地道に答えまでたどり着かせる方法も示しておきます。

大阪府立高校入試のＢ問題は基礎の確認や作業の確認など、
利用方法がいろいろある問題ですよ。

第１問

\(\,\large{1}\,\)
計算問題なので簡単に済ませます。
(1)
　\(\hspace{10pt}18-(-4)^2\div 8\\
=18-16\div 8\\
=18-2\\
=\underline{　16　}\)

（かっこ）がある場合の計算順序は確認しておきましょう。
それと、符号注意ですね。

(2)
　\(\hspace{10pt}2(5a-b)-3(a+6b)\\
=10a-2b-3a-18b\\
=\underline{　7a-20b　}\)

展開部分の暗算は控えた方がミスは減ります。

(3)
　\(\hspace{10pt}\displaystyle 14ab\div 7a^2\times ab\\
=\displaystyle \frac{14ab\times ab}{7a^2}\\
=\underline{　2b^2　}\)

割り算は逆数の掛け算として処理しても良いですが、
「\(\,\div\,\)」の直後を分母に回せばややこしい計算でも気軽に約分できます。

(4)
　\(\hspace{10pt}(x+1)(x-1)-(x+3)(x-8)\\
=(x^2-1)-(x^2-5x-24)\\
=x^2-1-x^2+5x+24\\
=\underline{　5x+23　}\)

２行目から３行目のところでの計算ミスが多いので気をつけましょう。

(5)
　\(\hspace{10pt}\displaystyle (\sqrt{6}-\sqrt{2})^2+\sqrt{27}\\
\displaystyle =(6-\color{red}{2\sqrt{12}}+2)+3\sqrt{3}\\
\displaystyle =8-\color{red}{4\sqrt{3}}+3\sqrt{3}\\
\displaystyle =\underline{　8-\sqrt{3}　}\)

無理数の計算は暗算できるレベルが慣れによって変わってきますが、
暗算できるからといっても確実にした方が無難です。
計算を１行増やしたからといって大して時間は変わりませんよ。

第２問

\(\,\large{2}\,\)
小問が８つあります。
(1)
等式変形です。
　\(\begin{eqnarray}\displaystyle
b&=&\frac{5a+4}{7}\\
7b&=&5a+4\\
5a+4&=&7b\\
5a&=&7b-4\\
a&=&\underline{\underline{　\frac{7b-4}{5}　}}
\end{eqnarray}\)

等式変形については無料レポートでも簡単にですが解説しているので、
会員サイトで確認して下さい。
（無料のメルマガ会員でもみることができます。）

(2)
２次方程式を解きます。
　\(\hspace{10pt}2x^2-3x-1=0\)

いつかタスキガケ因数分解が中学校の内容に戻るかもしれませんが、
いずれにしても因数分解できないので解の公式です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm \sqrt{(3)^2-4\cdot 2\cdot (-1)}}{2\times 2}\\
&=&\frac{3\pm \sqrt{9+8}}{4}\\
&=&\underline{\underline{　\frac{3\pm \sqrt{17}}{4}　}}
\end{eqnarray}\)

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

２次方程式の解の公式は導けなくても良いですが、
使えるようにはなっておきましょう。
※
公式に関しては「使えることが先」といつもはお伝えしていますが、
解の公式は導けるようになっておいた方が良いです。
（平方完成の練習になるからです。）

(3)
代表値の比較です。
全て求めておきますので自分でも確認しておきましょう。
　平均値：\(\,a=4.5\,\)
　最頻値：\(\,b=3\,\)
　中央値：\(\,c=4\,\)
これから
　\(\hspace{10pt}b\,＜\,c\,＜\,a\)

答え　\(\,\underline{　エ　}\,\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

どこでも言っていますが、
代表値は小学校の内容ですが中学でも高校でも必要です。

(4)
２つの箱\(\,\mathrm{A\,,\,B}\,\)からカードを１枚ずつ取り出し、
和が２０の約数になる確率です。
　\(\,\mathrm{A}\,\)：\(\,\color{red}{1}\,,\,\color{red}{2}\,,\,\color{red}{3}\,\)
　\(\,\mathrm{B}\,\)：\(\,\color{blue}{1}\,,\,\color{blue}{3}\,,\,\color{blue}{5}\,,\,\color{blue}{7}\,\)

２０の約数は\(\,\color{magenta}{1}\,,\,\color{magenta}{2}\,,\,\color{magenta}{4}\,,\,\color{magenta}{5}\,,\,\color{magenta}{10}\,,\,\color{magenta}{20}\,\)です。

樹形図でいいですが、
ここでは表にしておきます。
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{3} & \color{blue}{5} & \color{blue}{7} \\ \hline
\color{red}{1} & \color{magenta}{2} & \color{magenta}{4} & 6 & 8 \\ \hline
\color{red}{2} & 3 & \color{magenta}{5} & 7 & 9 \\ \hline
\color{red}{3} & \color{magenta}{4} & 6 & 8 & \color{magenta}{10} \\ \hline
\end{array}\)

組み合わせは１２通り、そのうち５通りが２０の約数になります。
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{5}{12}　}}\)

あれこれ考えるのも良いですが、
この程度の組み合わせは調べ上げた方が早いですね。
というか、考えるための作業段階で答えが出ます。

(5)
３連続整数の「最も小さい整数」を求めます。

最も小さい整数を\(\,n\,\)とすると３連続整数は
　\(\hspace{4pt}n\,,\,n+1\,,\,n+2\,\)
この和が\(\,2022\,\)なので
　\(\begin{eqnarray}\displaystyle
n+(n+1)+(n+2)&=&2022\\
3n+3&=&2022\\
3n&=&2019\\
n&=&\underline{　673　}
\end{eqnarray}\)

まん中（２番目）の整数を\(\,m\,\)とおくと計算しやすいですが、
　\(\begin{eqnarray}\displaystyle
(m-1)+m+(m+1)&=&2022\\
3m&=&2022\\
m&=&674　(\,\leftarrow\,２番目の整数\,)
\end{eqnarray}\)
求める整数を文字でおいて直接答えになるようにしました。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

文字式の使い方は基本中の基本ですので確認しておきましょう。

(6)
角度を求めますので図の中で見ていくと良いです。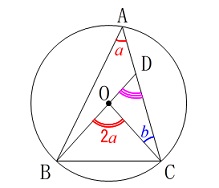円に内接する三角形と中心がありますので、
円周角の定理は利用するでしょう。

三角形の１つの外角と内角の関係から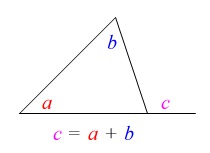\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{∠BOC}}&=&\mathrm{\color{blue}{∠OCD}+\color{magenta}{∠CDO}}\\
\color{red}{2a}&=&\color{blue}{b}+\mathrm{\color{magenta}{∠CDO}}\\
\mathrm{\color{magenta}{∠CDO}}&=&\underline{　b-2a　} (\,度\,)
\end{eqnarray}\)

三角形の内角の和からでも良いですよ。

(7)
２つの条件を満たす自然数を求めます。
　・\(\hspace{4pt}4\,＜\,\sqrt{n}\,＜\,5\)
　・\(\hspace{4pt}\sqrt{6n}\,\)は自然数

第一の条件
　・\(\hspace{4pt}4\,＜\,\sqrt{n}\,＜\,5\)
の処理は２つの方向があります。
ルートで統一すると
　\(\hspace{4pt}4=\sqrt{16}\,,\,5=\sqrt{25}\)
なので
　\(\hspace{4pt}\sqrt{16}\,＜\,\sqrt{n}\,＜\sqrt{25}\)

全辺が正の数だから不等号の向きは平方しても変わらないので
　\(\hspace{4pt}16\,＜\,n\,＜\,25\)
いずれにしても
　\(\hspace{4pt}n=17\,,\,18\,,\,19\,,\,20\,,\,21\,,\,22\,,\,23\,,\,24\)
の中に答えはあります。

第二の条件
　・\(\hspace{4pt}\sqrt{6n}\,\)は自然数
ルートが外れることから\(\,n\,\)は\(\,6\,\)の倍数になるので
　\(\hspace{10pt}n=18\,,\,24\)

\(\,n=18\,\)のとき\(\,\sqrt{6n}\,\)は
　\(\hspace{10pt}\sqrt{6\times 18}=6\sqrt{3}\)
自然数になりません。
\(\,n=24\,\)のとき\(\,\sqrt{6n}\,\)は
　\(\hspace{10pt}\sqrt{6\times 24}=12\)
と自然数になります。

答え　\(\,n=\underline{　24　}\,\)

第二の条件から
　\(\hspace{4pt}n=6\times k^2\)
となることが自然数になる条件で、
　\(\hspace{4pt}k=1\,,\,2\,,\,\cdots\)
と調べれば良いのですが絞れた条件から探していきました。

自然数で範囲があるので調べ尽くしくす。
泥くさい、といわれようが数学はそこから始まると思って良いです。

(8)
関数の問題ですが、
条件が長い文章になっているので整理しながら、
分かることを次々にグラフに書き込んで行きましょう。

考え方の流れだけを説明しておきます。

点\(\,\mathrm{A}\,\)は関数\(\displaystyle m:\,y=\frac{1}{2}x^2\,\)上の点で\(\,x座\,\)標が\(\,3\,\)なので
　\(\,\mathrm{A}\,\)：\(\displaystyle \left(\,3\,,\,\frac{9}{2}\,\right)\)
点\(\,\mathrm{B}\,\)は点\(\,\mathrm{A}\,\)と\(\,x\,\)座標が同じ\(\,x\,\)軸上の点なので
　\(\,\mathrm{B}\,\)：\(\displaystyle(\,3\,,\,0\,)\)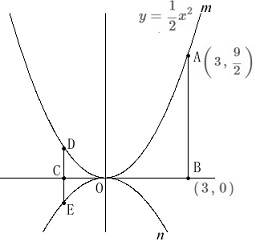点\(\,\mathrm{C}\,\)は\(\,x\,\)軸上の点で\(\,\mathrm{CB=AB}\,\)なので、
\(\,\mathrm{A}\,\)の\(\,y\,\)座標から\(\,\mathrm{AB}=\displaystyle \frac{9}{2}\,\)であることから
　\(\,\mathrm{C}\,\)：\(\left(\displaystyle \,-\frac{3}{2}\,,\,0\,\right)\,\)
点\(\,\mathrm{D}\,\)は点\(\,\mathrm{C}\,\)と\(\,x\,\)座標が同じで関数\(\,m\,\)上の点だから
　\(\,\mathrm{D}\,\)：\(\left(\displaystyle \,-\frac{3}{2}\,,\,\frac{9}{8}\,\right)\,\)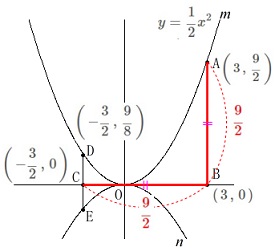さらに\(\,\mathrm{DE=\color{blue}{2}}\,\)で点\(\,\mathrm{E}\,\)の座標は\(\,x\,\)座標が\(\,\mathrm{D\,,\,C}\,\)と同じなので
　\(\,\mathrm{E}\,\)：\(\,\displaystyle \color{blue}{\left(\,-\frac{3}{2}\,,\,-\frac{7}{8}\,\right)}\)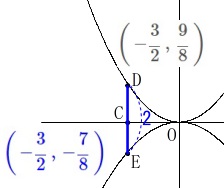関数\(\,n:y=ax^2\,\)は点\(\,\mathrm{E}\,\)を通るので代入して
　\(\begin{eqnarray}\displaystyle
-\frac{7}{8}&=&a\times \left(\,-\frac{3}{2}\,\right)^2\\
a&=&-\frac{7}{8}\times \frac{4}{9}\\
&=&\underline{\underline{　-\frac{7}{18}　}}
\end{eqnarray}\)

それぞれの座標は示す必要はありますが、
長さの関係から座標を出すところの計算は書かなくても良いと思います。

長さの単位が座標\(\,1\,\)の変化で\(\,\mathrm{1\,cm}\,\)ですが、
解答上でも余り気にしなくても良いです。
長さの単位がなくても成り立つ問題ですが、
考え易くしてくれているだけでしょう。
長さの関係から座標を求めている事を書くなら単位を添えておきましょう。
（解答上で単位が抜けていて減点されるかどうかは学校による採点基準次第ですね。）

第３問

\(\,\large{3}\,\)
規則性を関数とみる問題です。

\(\,x\,,\,y\,\)が出てきますが\(\,x\,\)は自然数なので飛び飛びの関数となります。
(1)は\(\,\mathrm{A}\,\)問題と同じなので\(\,\mathrm{A}\,\)問題の解説を見ておいて下さい。

⇒　2022年(令和4年)度大阪府公立高校入試の数学A問題と解説

\(\,\large{3}\,\)の(1)です。
(2)は違います。

(2)
２種類のコーンを積んで同じ高さにします。
　コーン\(\,\mathrm{A}\,\)：\(\,\mathrm{320mm}\,\)で１つ積むごとに\(\,\mathrm{15mm}\,\)高くなる。
　コーン\(\,\mathrm{B}\,\)：\(\,\mathrm{150mm}\,\)で１つ積むごとに\(\,\mathrm{10mm}\,\)高くなる。
　\(\,\mathrm{A}\,\)を\(\,s\,\)個、\(\,\mathrm{B}\,\)を\(\,t\,\)個合わせて\(\,39\,\)個積んで同じ高さになった。
というのが条件です。
このときの\(\,s\,,\,t\,\)を求めます。

\(\,\mathrm{B}\,\)の方が小さいので同じ高さになるなら、
\(\,\mathrm{B}\,\)の方が多いということはなんとなく分かるでしょう。

自然数なので調べても答えは出てきます。
その場合\(\,t\,\)の大きい方から調べると早いです。

ここでは連立方程式として解くことを求めていると思うので、
連立しておきます。

考え方は(1)と同じです。
\(\,\mathrm{A}\,\)を\(\,s\,\)個積み上げると高さ\(\,h\,\)は
　\(\begin{eqnarray}\displaystyle
h&=&320+15(s-1)\\
&=&15\,s+305
\end{eqnarray}\)
\(\,\mathrm{B}\,\)を\(\,t\,\)個積み上げると高さ\(\,h’\,\)は
　\(\begin{eqnarray}\displaystyle
h’&=&150+10(t-1)\\
&=&10\,t+140
\end{eqnarray}\)
高さが等しくなるので
　\(\hspace{4pt}15\,s+305=10\,t+140　･･･①\)
これと\(\,\mathrm{A\,,\,B}\,\)合わせて\(\,39\,\)個であることから
　\(\hspace{4pt}s+t=39　･･･②\)
\(\,①②\,\)を連立した形で書くと
　\( \begin{cases}
\hspace{4pt} 15\,s+305=\,10\,t+140　･･･①\\
\hspace{4pt} s+t=\,39　･･･②
\end{cases}\)
これから
　\(\hspace{10pt}s=\underline{　9　}\,,\,t=\underline{　30　}\)

合わせて\(\,39\,\)個のときなので\(\,\mathrm{B}\,\)が多い方から規則性をみておきます。
\(\,\mathrm{A}\,\)が\(\,1\,\)個のとき\(\,\mathrm{B}\,\)は\(\,38\,\)個
　\(\,\mathrm{A}\,\)の高さ：\(\,320\,\)、\(\,\mathrm{B}\,\)の高さ：\(\,520\,\)
\(\,\mathrm{A}\,\)が\(\,2\,\)個のとき\(\,\mathrm{B}\,\)は\(\,37\,\)個
　\(\,\mathrm{A}\,\)の高さ：\(\,335\,\)、\(\,\mathrm{B}\,\)の高さ：\(\,510\,\)
と\(\,\mathrm{A}\,\)は\(\,15\,\)増え\(\,\mathrm{B}\,\)は\(\,10\,\)減るで、
差は\(\,25\,\)縮まります。
　\(\begin{array}{|c|c|c|c|c|} \hline
　\mathrm{A}\,の個数　 &　 1 　&　 2　 &　 3　 &　 \cdots　 \\ \hline
　\mathrm{B}\,の個数　& 38 & 37 & 36 & \cdots \\ \hline
差 & 200 & 175 & 150 & \cdots \\ \hline
\end{array}\)

\(\,200\,\)の差を\(\,0\,\)にするには\(\,8\,\)個\(\,\mathrm{B}\,\)を減らせば良いので、
　\(\hspace{10pt}s=\underline{　9　}\,,\,t=\underline{　30　}\)

関数としてのグラフはかけないのでどちらでも良いと思いますよ。
連立方程式を解く方が確実かもしれませんが、
答えは確認しておいた方が良いですね。
\(\,s=9\,\)のとき\(\,h\,\)は
　\(\begin{eqnarray}\displaystyle
h&=&320+15(9-1)\\
&=&320+120\\
&=&440
\end{eqnarray}\)
\(\,t=30\,\)のとき\(\,h’\,\)は
　\(\begin{eqnarray}\displaystyle
h’&=&150+10(30-1)\\
&=&150+290\\
&=&440
\end{eqnarray}\)　

同じ高さになっています。

\(\,s\,\)より\(\,t\,\)が多い方になるのはなんとなく分かるので、
計算しやすい\(\,t=30\,\)のときを計算してみると、
ドンピシャで同じ高さになるので即答えですが、
いつもそんなラッキーは転がってません。

第４問

\(\,\large{4}\,\)
平面図形と空間図形の問題があります。
［\(\,\mathrm{Ⅰ}\,\)］
平行四辺形と長さの条件が与えられていますの出、
図の中で示しておきます。
（条件整理は自分でやって図示して下さい。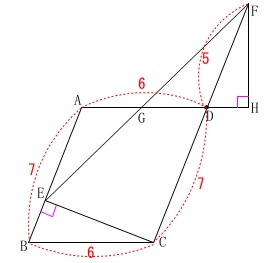）(1)
相似の証明です。
　\(\,\mathrm{△BCE}\,\)∽\(\,\mathrm{△DFH}\,\)

証明は図の中で終わらせておく、
という方針通り図の中に条件を示しておくので確認して下さい。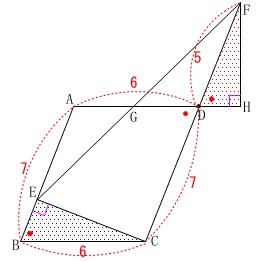平行四辺形の対角は等しく、
対頂角は等しいので
　\(\hspace{4pt}\mathrm{∠EBC=∠CDG=∠HDF}　･･･①\)
垂線であるという仮定から
　\(\hspace{4pt}\mathrm{∠CEB=∠FHD}=90^{\circ}　･･･②\)
\(\,①②\,\)より相似条件がそろいました。
　「２組の角がそれぞれ等しい。」

証明はまとめて見て下さい。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

書き方に決まりはありません。
ただし、合同、相似の証明では、
記号の順番はそろえる必要があるので間違えないようにしましょう。

(2)
条件が加わり長さと面積を求めます。
　\(\hspace{4pt}\mathrm{DH}=2\)※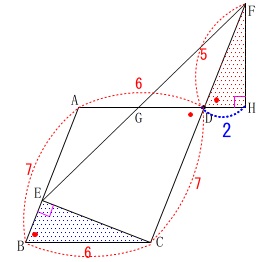
長さの単位は\(\,\mathrm{cmで}\,\)すが途中の計算では省略します。
①
線分\(\,\mathrm{BE}\,\)の長さを求めます。
(1)で示した相似から
　\(\,\mathrm{△BCE}\,\)∽\(\,\mathrm{△DFH}\,\)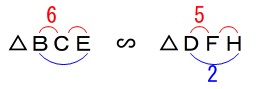
　\(\begin{eqnarray}\displaystyle
\mathrm{BC:DF}&=&\mathrm{BE:DH}\\
\color{red}{6}:\color{red}{5}&=&\mathrm{BE}:\color{blue}{2}\\
5\times \mathrm{BE}&=&6\times 2\\
\mathrm{BE}&=&\underline{\underline{　\frac{12}{5}　　}}(\mathrm{cm})
\end{eqnarray}\)

②
次に\(\,\mathrm{△FGD}\,\)の面積を求めます。
\(\,①\,\)がなければ結構な応用問題になりますが、
見事な誘導をしてくれています。

相似を利用しますが分かる長さを出しておきましょう。
　\(\begin{eqnarray}\displaystyle
\mathrm{AE}&=&\mathrm{AB-BE}\\
&=&7-\frac{12}{5}\\
&=&\frac{23}{5}
\end{eqnarray}\)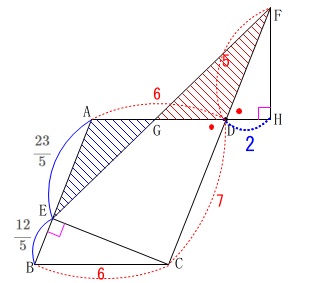平行線の錯角と対頂角から
　\(\,\mathrm{△AED}\,\)∽\(\,\mathrm{△FDB}\,\)
相似比は
　\(\hspace{4pt}\mathrm{AE:FD}=\displaystyle \frac{23}{5}:5=\color{magenta}{23}:\color{magenta}{25}\)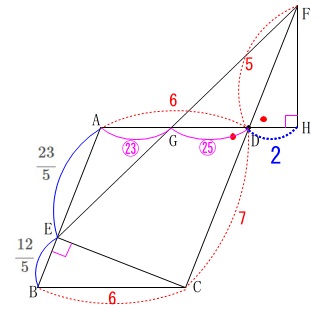これから
　\(\begin{eqnarray}\displaystyle
\mathrm{GD}&=&\color{red}{6}\times \frac{\color{magenta}{25}}{\color{magenta}{23}+\color{magenta}{25}}\\
&=&\color{blue}{\frac{25}{8}}
\end{eqnarray}\)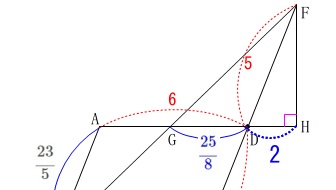高さとなる\(\,\mathrm{FH}\,\)は三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{FH^2+DH^2}&=&\mathrm{FD^2}\\
\mathrm{FH^2}&=&\mathrm{FD^2-DH^2}\\
&=&\color{red}{5}^2-\color{blue}{2}^2\\
&=&21
\end{eqnarray}\)
長さなので\(\,\mathrm{FH\,＞\,0}\,\)だから
　\(\hspace{4pt}\mathrm{FH}=\color{magenta}{\sqrt{21}}\)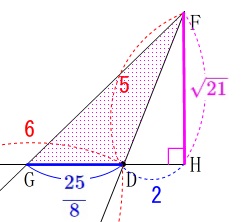よって、求める面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△FGD}&=&\frac{1}{2}\times \mathrm{GD}\times \mathrm{FH}\\
&=&\frac{1}{2}\times \color{blue}{\frac{25}{8}}\times \color{magenta}{\sqrt{21}}\\
&=&\underline{\underline{　\frac{25\sqrt{21}}{16}　}}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

\(\,\mathrm{△AGH}\,\)から\(\,\mathrm{△FDH}\,\)を引いて求めた人もいるでしょう。
構いませんよ。
思い立った方向でガンガン進めて行けば良いです。

［\(\,\mathrm{Ⅱ}\,\)］
立体（四角柱）についての問題で、
ねじれの位置にある辺、長さ、体積を求めます。
問題の条件があるので図しておきます。
（これは問題の条件を読み取る意味で自分でやっておいて下さい。）
※長さの単位は\(\,\mathrm{cm}\,\)です。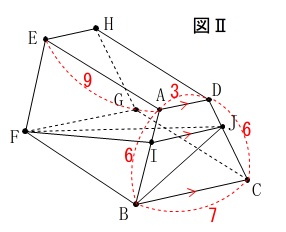(3)
辺\(\,\mathrm{AD}\,\)とねじれの位置にある辺を全て選びます。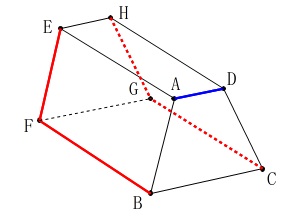問題の選択肢にないので\(\,\mathrm{I\,,\,J}\,\)を含む辺は省いておきました。

ねじれの位置になるのは平行でもなく交わりもしない辺です。
　辺\(\,\mathrm{EF\,,\,HG\,,\,FB\,,\,GC}\,\)

答え　\(\,\underline{　ウ　エ　}\,\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

「ねじれの位置」では注意点がありますので確認しておいて下さい。

(4)
長さの条件が加わり、線分と体積を求めます。
　\(\hspace{4pt}\mathrm{AI}=\color{blue}{2}\)　

［\(\,\mathrm{Ⅱ}\,\)］全体の図Ⅱの条件は続いていますよ。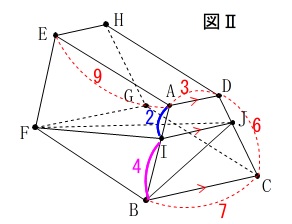残りの\(\,\mathrm{IB=\color{magenta}{4}}\,\)となることは説明いらないでしょう。
①
線分\(\,\mathrm{IJ}\,\)の長さです。

基本通り面を抜き出して見ていきましょう。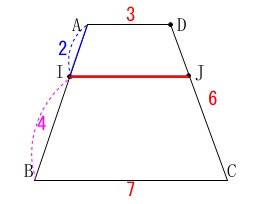平行線を引いて相似利用で簡単に終わりますが、
（会員の方はたぶん公式を使っただろうから、）
先にもっと簡単に公式で答えを求めておきます。
　\(\begin{eqnarray}\displaystyle
\mathrm{IJ}&=&\frac{\color{red}{3}\times \color{magenta}{4}+\color{red}{7}\times \color{blue}{2} }{\color{magenta}{4}+\color{blue}{2}}\\
&=&\frac{12+14}{6}\\
&=&\underline{\underline{　\frac{13}{3}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

答えは出ましたので、確認のため補助線で普通に求めておきましょう。
点\(\,\mathrm{A}\,\)を通り\(\,\mathrm{DC}\,\)に平行な線分\(\,\mathrm{AK}\,\)を引き、
線分\(\,\mathrm{IJ}\,\)との交点を\(\,\mathrm{L}\,\)としておきます。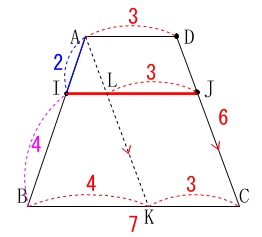\(\,\mathrm{LJ=3}\,\)となるのは説明不要ですね。

\(\,\mathrm{△AIL}\,\)と\(\,\mathrm{△ABK}\,\)は相似で、
相似比が\(\,\color{blue}{2}：(\color{blue}{2}+\color{magenta}{4})＝1：3\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{IL}:\mathrm{\color{red}{BK}}&=&1:3\\
\mathrm{IL}:\color{red}{4}&=&1:3\\
3\times \mathrm{IL}&=&4
\mathrm{IL}&=&\frac{1}{3}\times 4\\
&=&\frac{4}{3}
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{IJ}&=&\mathrm{IL+LJ}\\
&=&\frac{4}{3}+3\\
&=&\underline{\underline{　\frac{13}{3}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

補助線として平行線を引く方法の方が応用が利くので、
考え方としては覚えておきましょう。

②
最後の問題、部分的な体積です。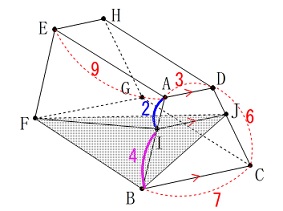立体（三角すい）\(\,\mathrm{IFBJ}\,\)の体積を求めます。

線分\(\,\mathrm{BF}\,\)は面\(\,\mathrm{ABCD}\,\)に垂直なので、
底面を\(\,\mathrm{\color{red}{△BIJ}}\,\)として、高さは\(\,\mathrm{FB=\color{blue}{9}}\,\)です。底面の\(\,\mathrm{△BIJ}\,\)の面積を求めましょう。

方法は色々考えられますが四角形\(\,\mathrm{ABCD}\,\)が等脚台形なので、
頂点\(\,\mathrm{A}\,\)または\(\,\mathrm{D}\,\)から線分\(\,\mathrm{BC}\,\)に垂線を引きましょう。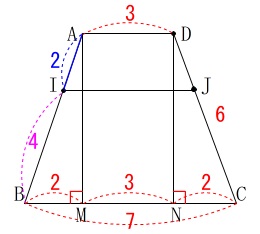\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{M\,,\,N}\,\)とすると、
\(\,\mathrm{△ABM}\,\)は直角三角形なので三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2}&=&\mathrm{AM^2+BM^2}\\
\mathrm{AM^2}&=&\mathrm{AB^2-BM^2}\\
&=&6^2-2^2\\
&=&32\\
\mathrm{AM}&=&\pm 4\sqrt{2}
\end{eqnarray}\)
\(\,\mathrm{AM}\,\)は長さなので\(\,\mathrm{AM\,＞\,0}\,\)より
　\(\hspace{4pt}\mathrm{AM}=\color{blue}{4\sqrt{2}}\)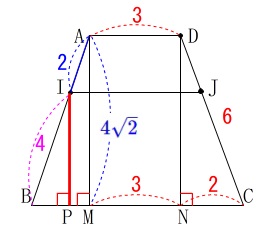\(\,\mathrm{△BIJ}\,\)の高さとなるのは、
\(\,\mathrm{I}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろした\(\,\mathrm{IP}\,\)となります。
　\(\,\mathrm{△ABM}\,\)　∽　\(\,\mathrm{△IBP}\,\)
で相似比が\(\,3:2\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{IP}&=&\frac{2}{3}\times \mathrm{AM}\\
&=&\frac{2}{3}\times \color{blue}{4\sqrt{2}}\\
&=&\color{red}{\frac{8\sqrt{2}}{3}}
\end{eqnarray}\)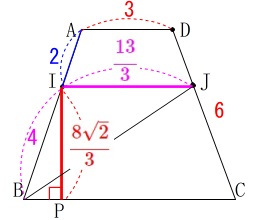\(\,\mathrm{△BIJ}\,\)の底辺とみることができる\(\,\mathrm{IJ}\,\)は①から
　\(\hspace{4pt}\displaystyle \mathrm{IJ}=\color{magenta}{\frac{13}{3}}\)
と分かっているので
　\(\begin{eqnarray}\displaystyle
\mathrm{△BIJ}&=&\frac{1}{2}\times \mathrm{IJ}\times \mathrm{IP}\\
&=&\frac{1}{2}\times \color{magenta}{\frac{13}{3}}\times \color{red}{\frac{8\sqrt{2}}{3}}\\
\end{eqnarray}\)
（ここまでを計算しても良いですが、高さをかけるので後で約分します。）
よって、求める立体の体積\(\,V\,\)は高さが\(\,\mathrm{BF=\color{blue}{9}}\,\)なので
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{△BIJ}\times \mathrm{BF}\\
&=&\frac{1}{3}\times \frac{1}{2}\times \color{magenta}{\frac{13}{3}}\times \color{red}{\frac{8\sqrt{2}}{3}}\times \color{blue}{9}\\
&=&\underline{\underline{　\frac{52\sqrt{2}}{3}　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)