2022年（令和4年）度長野県公立高校入試【数学】の問題と解説

２０２２年（令和４年度）長野県で行われた公立高校入試【数学】の問題と解説です。
大問４つで例年と変わりなく基本を偏りなく、幅広く問われています。
割ときれいな数値で計算できるように問題が作られていますので、
ムダに計算力を問うのではなく基本の定着を図るには適した問題だと感じます。
ただし、「少し意地を見せてね。」という問題が１つだけあります。

2022年（令和4年）度長野県公立高校入試の数学の問題

令和４年度長野県公立高校入試の数学の問題です。

⇒　令和４年度長野県公立高校入試の数学の問題ＰＤＦ

問題の最後に余白計算スペースを与えてくれていますのでそのまま添付します。

2022年（令和4年）度長野県公立高校入試の【数学】の解説

冒頭でも書きましたが、計算力を試す問題ではなく、
数学の基本を割ときれいな数値で聞いてくれています。

全体の基本をしっかりと抑え、
（『覚え太郎』＋『基本レポート』）
数学問題を解くときに必要な作業をしっかりとすれば満点は十分狙えますよ。

問題数として少なくはないので早速解説に入りましょう。

第１問

【問１】
(1)から(11)まであります。

(1)
　\(\hspace{10pt}5+(-2)\\
=5-2\\
=\underline{　3　}\)

特別な説明は必要ありませんね。

(2)
　\(\hspace{10pt}(-6x+9)\div 3\\
=\underline{　-2x+3　}\)

割り算なので逆数の掛け算で処理すると全ての計算に適応できますが、
割り切れるのでそのまま計算しました。

(3)
　\(\hspace{4pt}84\,n\,\)が平方数となる最小の\(\,n\,\)を求めます。

素因数分解すると
\(\hspace{10pt}84=2^2\times \color{red}{3\times 7}\)
なので平方になっていない数を平方の形にすれば良いだけです。
　\(\hspace{10pt}n=\color{red}{3\times 7}=\underline{　21　}\)

\(\,n\,\)は\(\,21\times k^2\,\)となっていれば全体が平方数になりますが、
最小の\(\,n\,\)なので\(\,k=1\,\)のときで良いです。

(4)
２次方程式の解で最も正しいものを選びます。
代入して成り立つものを探すのも方法の１つですが、
方程式を解きなさい、ということです。
　\(\begin{eqnarray}\displaystyle
x^2&=&4x\\
x^2-4x&=&0\\
x(x-4)&=&0\\
x&=&0\,,\,4
\end{eqnarray}\)

答え　\(\,\underline{　ウ　}\,\)

エの\(\,x=4\,\)も解の１つですが、不足しています。

(5)
文字式と関係式です。
　\(\,a\,\)人が\(\,500\,\)円ずつ出すと\(\,\color{red}{500\,a}\,\)円
　\(\,\color{blue}{b}\,\)円の花束を買おうとすると\(\,\color{magenta}{200}\,\)円不足

花束の値段が集めたお金より高い、ということなので
足りない金額は集めたお金に加えて等しくなります。
　\(\hspace{10pt}\color{red}{500\,a}+\color{magenta}{200}=\color{blue}{b}\)

選択肢にある関係式は
　\(\hspace{10pt}500\,a=b-200\)

答え　\(\,\underline{　エ　}\,\)

足りなかった金額は「ちょうど\(\,200\,\)円」という意味になるので等式です。

(6)
中央値を求めます。

小さい順に並べてくれているので作業の手間が省けますね。
　\(\hspace{10pt}\displaystyle \frac{15+19}{2}=\underline{　17　}\)

中央値は順番に並べたときまん中に位置する値ですが、
データの数が奇数のときと偶数のときで求め方が違います。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値はデータを扱うのにこれからも必要です。
現在は小学校の内容になっていますが必ず確認しておきましょう。

(7)
「起こらない確率」です。

ことがら\(\,\mathrm{A}\,\)は、
起こるか、起こらないかのどちらかなので
　\(\hspace{10pt}\displaystyle 1-\frac{3}{8}=\underline{\underline{　\frac{5}{8}　}}\)

あることが「起こる確率」と「起こらない確率」を足すと\(\,\color{red}{1}\,\)になります。

(8)
無理数の計算問題です。
　\(\hspace{4pt}\sqrt{4}\,＜\,\color{red}{\sqrt{6}}\,＜\,\sqrt{9}\)
つまり
　\(\hspace{4pt}2\,＜\,\color{red}{\sqrt{6}}\,＜\,3　\Rightarrow　 \sqrt{6}=2.\cdots\)
なので\(\,\sqrt{6}\,\)の整数部分は\(\,2\,\)です。

数全体は（整数部分）＋（小数部分）なので
小数部分を\(\,a\,\)とすると
　\(\hspace{10pt}\color{blue}{\sqrt{6}}=\color{blue}{2+a}\)
変形しておくと
　\(\hspace{10pt}\color{magenta}{a}=\color{magenta}{\sqrt{6}-2}\)

よって、求める値は
　\(\hspace{10pt}\color{magenta}{a}(\color{blue}{a+2})\\
=(\color{magenta}{\sqrt{6}-2})\times \color{blue}{\sqrt{6}}\\
=\underline{　6-2\sqrt{6}　}\)

『覚え太郎』会員の人は条件をみて
　\(\begin{eqnarray}\displaystyle
(a+2)^2&=&(\sqrt{6})^2\\
a^2+4a+4&=&6
\end{eqnarray}\)
としたかもしれませんがそこまで必要無い問題でした。
ただ、利用できないわけではないのでムダではありませんよ。
（与式を見ずに私もやりました。笑）

(9)
問題に書いてある通り反比例の問題です。
　\(\hspace{10pt}\displaystyle y=\frac{\color{red}{a}}{x}\)

先に比例定数\(\,\color{red}{a}\,\)を決めましょう。
出力の\(\,\mathrm{W}\,\)（ワット）数が\(\,x\,\)で、時間が\(\,y\,\)です。
\(\,x=500\,\)のとき\(\,y=3\,\)なので
　\(\begin{eqnarray}\displaystyle
3&=&\frac{\color{red}{a}}{500}\\
\color{red}{a}&=&1500
\end{eqnarray}\)
このとき関数は
　\(\hspace{10pt}\displaystyle y=\frac{1500}{x}\)

\(\,x=600\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1500}{600}\\
&=&\frac{5}{2}\\
&=&2.5\,(\,分\,)
\end{eqnarray}\)

答え　\(\,\underline{　2　}分\underline{　30　}秒\,\)

比例定数は\(\,x=1500\,,\,y=1\,\)からでも良いですよ。

⇒　比例と反比例の関数の比例定数を決める問題の解き方と座標の求め方

比例も反比例も同じく「比例定数」です。

(10)
作図です。

条件は
「直径\(\,\mathrm{AB}\,\)と\(\,\ell\,\)とで円を４等分しなさい。」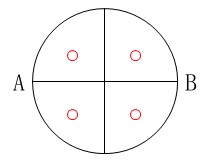なので線分\(\,\mathrm{AB}\,\)の垂直二等分線を作図すれば良いだけです。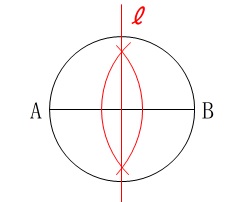会員は作図問題集『さくっと！』で作図の考え方は確認しておきましょう。
直線の交点は円の中心ですが書き込む必要はありません。

(11)
図形の基本確認問題です。
　\(\hspace{4pt}\mathrm{∠BOC}=120^{\circ}\)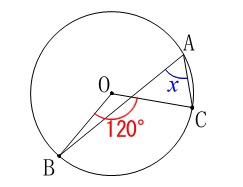①
円周角となる\(\,∠x\,\)の大きさを求めます。

中心角\(\,\mathrm{∠BOC}\,\)が\(\,120°\,\)なので
　\(\hspace{10pt}∠x=\underline{　60^{\circ}　}\)

ここでは\(\,x\,\)という文字は、
角度ではなく、位置を表しています。

②
長さの条件が加わり、おうぎ形の面積を求めます。
　\(\hspace{10pt}\mathrm{OB}=6\,(\,\mathrm{cm}\,)\)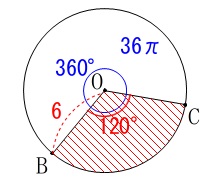中心角が\(\,120°\,\)なので
　\(\hspace{10pt}\displaystyle \pi \times (\,6\,)^2\times \frac{120}{360}\\
\displaystyle =36\,\pi \times \frac{1}{3}\\
=\underline{　12\,\pi　}\,(\,\mathrm{cm^2}\,)\)

円の面積を基準に比例式でも良いですよ。
　\(\begin{eqnarray}\displaystyle
360:120&=&36\pi:S\\
360\times S&=&120\times 36\,\pi\\
S&=&\frac{120\times 36\,\pi}{360}\\
&=&12\,\pi
\end{eqnarray}\)

【問１】は以上です。

第２問

【問２】
ここもいくつか問題があります。
図形、資料、連立方程式です。
(1)
立方体を切り取ってできる三角錐の問題です。
①
辺\(\,\mathrm{AD}\,\)とねじれの位置にある辺を答えます。
ただし、三角錐を作っている辺の中からですよ。答え　\(\,\underline{　\mathrm{辺\,CM}　}\,\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

ねじれの位置については注意点がありましたよね。
ここでは問題になっていませんが確認しておくと良いです。

②
三角錐の体積を求めます。

点\(\,\mathrm{M}\,\)は辺\(\,\mathrm{AB}\,\)の中点で長さが分かり易いので、
錐体の体積を求めるときの注意点を忘れなければ問題ないでしょう。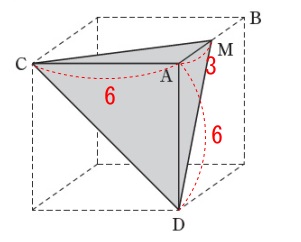底面はどこに見ても良いです。
（高さがとりにくいので\(\,\mathrm{△DCM}\,\)はやめておきましょう。）
求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\color{red}{\frac{1}{3}}\times \mathrm{\color{blue}{△ACM}}\times \mathrm{\color{magenta}{AD}}\\
&=&\color{red}{\frac{1}{3}}\times \color{blue}{\frac{1}{2}\times 6\times 3}\times \color{magenta}{6}\\
&=&\underline{　18　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

底面とする三角形の\(\,\displaystyle \frac{1}{2}\,\)は良いでしょうけど、
錐体の\(\,\displaystyle \color{red}{\frac{1}{3}}\,\)を忘れないように注意しておきましょう。

(2)
標本調査です。
抜き出した一部のデータから全体のおよその数を推測します。

コイ\(\,\color{red}{50}\,\)匹に印をつけて池に戻し、
取り出した\(\,\color{blue}{30}\,\)匹中に\(\,\color{magenta}{9}\,\)に匹印があった。
というのが条件です。

池中のコイの総数を\(\,x\,\)として比例式を利用します。
　\(\begin{eqnarray}\displaystyle
\color{blue}{30}:\color{magenta}{9}&=&x:\color{red}{50}\\
9\,x&=&30\times 50\\
x&=&\frac{30\times 50}{9}\\
&=&\frac{500}{3}\\
&=&166.\cdots
\end{eqnarray}\)

一のくらいを四捨五入するので
　\(\hspace{10pt}およそ\underline{　170　}匹\)

②
標本調査が適している、ものを選びます。

答え　\(\,\underline{　ア　}と\underline{　エ　}\,\)

国勢調査は全数調査です。
学校単位であれば歯科検診は全員するでしょう。

新聞社やテレビ局に国民全てを調査する権限などありませんし、
時間がかかりすぎますので標本調査が適しています。

(3)
連立方程式の問題です。
解き方に自由度はありませんが数字に意味を持たせた、
数学らしい？問題ですね。

問題にある〔資料〕と書かれている連立方程式を見ながら考えて下さい。
２０１４年度のゴミの排出量が\(\,x\,\)、
２０１９年度のゴミの排出量が\(\,y\,\)です。
　\( \begin{cases}
\hspace{4pt} x-y=200\\
\hspace{4pt} \color{black}{\fbox{　A　}}=\displaystyle \frac{25}{100}\,y
\end{cases}\)

①
連立方程式中の数量の意味を書きます。
　\(\hspace{4pt}\displaystyle \frac{25}{100}\,y\)

数式の意味は\(\,y\,\)の\(\,25\,\)％です。
\(\,y\,\)は２０１９年度のゴミの排出量で、
〔資料〕から資源ゴミの排出量が２５％となっています。

答え　\(\,\underline{　２０１９年度の資源ゴミの排出量　}\,\)

②
\(\color{black}{\fbox{　A　}}\)に入る式を書きます。

①で連立方程式の第二方程式は資源ゴミについての関係なので、
２０１９年度の資源ゴミの排出量と等しいのは、
２０１４年度の資源ゴミの排出量の２５％増なので、
　\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{16}{100}\,x\times \frac{125}{100}　}}\)

２０１４年度の資源ゴミの排出量は、
排出量の合計\(\,x\,\)の１６％なので\(\displaystyle \,\frac{16}{100}\,x\,\)です。

「約分しなくてもよい。」というのは約分しても良いので、
小数や約分した分数を使っていても正解だとは思いますが、
数値に意味を持たせた方程式なので％で表されるそのままで良いでしょう。

③
２０１４年度と２０１９年度の可燃ゴミの排出量を、
連立方程式を解いて比較します。

　\( \begin{cases}
\hspace{4pt} x-y=200\\
\hspace{4pt}\displaystyle \frac{16}{100}\,x\times \frac{125}{100}=\displaystyle \frac{25}{100}\,y
\end{cases}\)

解き方は好きにしていいですが、
第二方程式の両辺を１００倍して
　\(\hspace{4pt}\displaystyle 16\,x\times \frac{5}{4}=25\,y\)
約分して
　\(\hspace{4pt}\displaystyle 4\,x\times 5=25\,y\)
とすると見やすいでしょう。
　\(\hspace{4pt}4\,x=5\,y\)
これと第一方程式と連立すると
　\(\hspace{4pt}x=1000\,,\,y=800\)

これはゴミの排出量の合計なので、
可燃ゴミの排出量は（単位は\(\,\mathrm{g}\,\)です。）
　２０１４年度：\(\,\displaystyle 1000\times \frac{66}{100}=\color{red}{660}\)
　２０１９年度：\(\,\displaystyle 800\times \frac{70}{100}=\color{blue}{560}\)

答え　\(\,\underline{　イ　減った　}\,\)

理由は連立方程式を解いて、
具体的な数値で比較すれば良いです。
※
どこまで書けば良いか迷うときはできるだけ詳しく書いておけば良いですよ。
解答に示すにしても示さないにしても、
どっちみち解くのだから連立方程式を解く段階を書いても時間はそれほど変わりません。
※※
途中過程は解答欄の大きさによりますね。
必要なのは可燃ゴミの排出量なので
連立方程式を解く段階は
「連立方程式・・・を解くと、\(\,x=\,,\,y=\,\,\)」
程度で十分です。
可燃ゴミの数値は必ず比較できるように書くこと。

第３問

【問３】
\(\,\mathrm{Ⅰ}\,\)
関数ですが段階的に飛びとびの値になる、
連続にはなっていない関数です。
タクシーの料金や通信料なんかで良くあるものですね。
ここでは荷物の送料が問題になっています。

この手の問題はグラフの読み取りは必要ですが、
関数を決定する、などといった関数問題ではないのが普通です。

ただし、関数であることには違いないので、
関数の定義だけでも確認しておきましょう。

問題については表と図（グラフ）があるので確認しておいて下さい。
(1)
\(\,\mathrm{A}\,\)社の料金は４段階になっています。
　\(\begin{array}{|c|c|} \hline
　大きさ　 &　料金　\\ \hline
　60\,\mathrm{cm}\,以下　&　800\,円　\\ \hline
　70\,\mathrm{cm}\,以下　&　1000\,円　\\ \hline
　100\,\mathrm{cm}\,以下　&　1300\,円　\\ \hline
　140\,\mathrm{cm}\,以下　&　1800\,円　\\ \hline
\end{array}\)
問題に書いてある通り大きさは小数点以下を切り上げです。
少しでもはみ出ると高い料金の方になります。

\(\,\mathrm{65cm}\,\)のときは\(\,\mathrm{70cm}\,\)以下の料金になるので\(\,1000\,\)円、
また\(\,1500\,\)円以下で送ることができるのは、
\(\,1300\,\)円で送ることができる\(\,\mathrm{100cm}\,\)以下です。

答え　\(\,\underline{　イ　}\,\)

ちなみに、大きさは荷物が直方体だとして、
縦、横、高さの３辺合計になります。

(2)
関数の定義ですね。

「え？こんな関数見たこと無い。」
と思われるかもしれませんが、教科書を見直してみて下さい。
（『覚え太郎』では、関数\(\,\mathrm{No.5}\,\)で確認。）

\(\,x\,\)を決めると\(\,y\,\)が決まる、
このとき\(\,y\,\)は\(\,x\,\)の関数です。

荷物の大きさを決めると料金が決まるので、
料金は荷物の大きさの関数です。

答え　\(\,\underline{　ア　}\,\)

ここは『覚え太郎』を何度も見ているかという問題です。

(3)
\(\,\mathrm{B}\,\)社との料金比較です。

\(\,\mathrm{B}\,\)社の料金は\(\,\mathrm{80cm}\,\)までが定額\(\,900\,\)円、
\(\,\mathrm{80cm}\,\)を超えると\(\,\mathrm{10cm}\,\)ごとに\(\,200\,\)円加算されます。

「例えば」と問題にあるように、
\(\,\mathrm{85cm}\,\)の荷物だと\(\,\mathrm{90cm}\,\)までの料金となり、
一回\(\,200\,\)円加算されて\(\,1100\,\)円になります。

もう少し見て見ると\(\,\mathrm{B}\,\)社の料金は
　\(\begin{array}{|c|c|} \hline
　大きさ　 &　料金　\\ \hline
　80\,\mathrm{cm}\,以下　&　900\,円　\\ \hline
　90\,\mathrm{cm}\,以下　&　1100\,円　\\ \hline
　100\,\mathrm{cm}\,以下　&　1300\,円　\\ \hline
　110\,\mathrm{cm}\,以下　&　1500\,円　\\ \hline
　120\,\mathrm{cm}\,以下　&　\color{red}{1700}\,円　\\ \hline
　\vdots\,　&　\vdots　\\ \hline
\end{array}\)

\(\,\mathrm{115cm}\,\)の荷物だと\(\,\mathrm{A}\,\)社では\(\,1800\,\)円、
\(\,\mathrm{B}\,\)社では\(\,\color{red}{1700}\,\)円なので、
\(\,\mathrm{B}\,\)社の方が\(\,100\,\)円安いですね。

\(\,\mathrm{Ⅱ}\,\)
次は普通に関数問題です。
(1)
関数\(\,y=a\,x^2\,\)のグラフについて、
一般的に言えることを選ぶ問題です。

グラフを考えるなら簡単にでもいいのでグラフを書いておきましょう。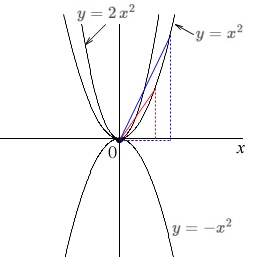基本性質なので詳しくは説明しませんが、
ア：
比例定数が正のときは原点が頂点で上に開いた形（下に凸）なので、
\(\,y=0\,\)が最小値となります。○
イ：
比例定数の絶対値が大きくなると変化が大きくなり、
開き方は小さくなります。×
ウ：
変化の割合は一定ではありません。○
エ：
グラフは放物線です。×
オ：
比例定数の絶対値が同じで符号が逆のとき、
\(\,x\,\)軸について対称なグラフになります。○

答え　\(\,\underline{　ア　,　ウ　,　オ　}\,\)

(2)
関数の決定ですね。
比例定数を求めます。

\(\hspace{4pt}y=a\,x^2\,\)と\(\,y=-2\,x+6\,\)の交点が\(\,\mathrm{A}\,\)で、
\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,-6\,\)です。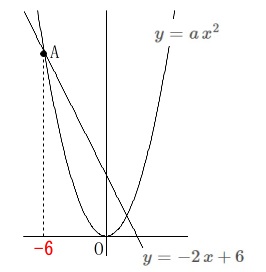点\(\,\mathrm{A}\,\)は\(\,y=-2\,x+6\,\)上の点なので、
　\(\begin{eqnarray}\displaystyle
y&=&-2\,(\,-6\,)+6\\
&=&18
\end{eqnarray}\)
　\(\hspace{4pt}\mathrm{A}\,(\,-6\,,\,18\,)\)

これは\(\,y=a\,x^2\,\)上の点でもあるので、
　\(\begin{eqnarray}\displaystyle
18&=&a\times (\,-6\,)^2\\
36\,a&=&18\\
a&=&\underline{\underline{　\frac{1}{2}　}}
\end{eqnarray}\)

(3)
放物線と直線があり直線の\(\,y\,\)切片\(\,\mathrm{B}\,\)が与えられています。
　関数：\(\,y=a\,x^2\,\)
　点\(\,\mathrm{B}\,\)：\(\,(\,0\,,\,6\,)\,\)

ただし、問\(\,①\,\)と問\(\,②\,\)では比例定数と直線の傾きは、
異なりますので注意しておいて下さい。
①
図４について、
　\(\hspace{4pt}a=1\,,\,\mathrm{AB:BD}=1:3\)
のとき点\(\,\mathrm{A}\,\)の座標を求めます。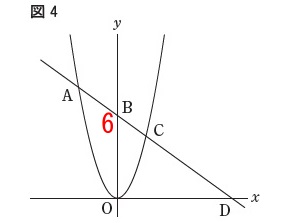条件から放物線を表す関数は
　\(\hspace{4pt}y=x^2\)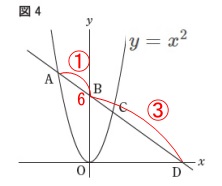点\(\,\mathrm{A}\,,\,\mathrm{D}\,\)の座標を\(\,t\,\)を使って文字設定します。
点\(\,\mathrm{A}\,\)は\(\,y\,\)軸より左の座標なので\(\,t\,＞\,0\,\)として
　\(\hspace{4pt}\mathrm{A}:(\,-t\,,\,\color{blue}{t^2}\,)\)
点\(\,\mathrm{D}\,\)は\(\,x\,\)軸上の点なので\(\,y=0\,\)だから
　\(\hspace{4pt}\mathrm{D}:(\,3t\,,\,\color{magenta}{0}\,)\)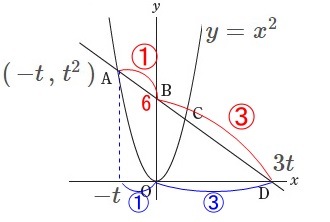\(\,y\,\)座標の比も\(\,1:3\,\)なので、
点\(\,\mathrm{A}\,\)と点\(\,\mathrm{B}\,\)の\(\,y\,\)座標の差と、
点\(\,\mathrm{B}\,\)と点\(\,\mathrm{D}\,\)の\(\,y\,\)座標の差も\(\,1:3\,\)となるので
　\(\begin{eqnarray}\displaystyle
(\color{blue}{t^2}-\color{red}{6}):(\color{red}{6}-\color{magenta}{0})&=&1:3\\
3(t^2-6)&=&6\\
3t^2-18&=&6\\
3t^2&=&24\\
t^2&=&8\\
t&=&\pm 2\sqrt{2}
\end{eqnarray}\)

設定で\(\,t\,＞\,0\,\)としているので
　\(\hspace{4pt}t=2\sqrt{2}\)
よって、点\(\,\mathrm{A}\,\)の座標は
　\(\hspace{10pt}\mathrm{A}\,\underline{　(\,-2\sqrt{2}\,,\,8\,)　}\)

\(\,y\,\)座標の差の図解はしていませんので確認しておいて下さい。
線分の長さの比なので差をとる方向は同じにしておきましょう。

②
図５において直線の傾きが\(\,-1\,\)で、
\(\,\mathrm{OC}\,\)と\(\,\mathrm{AC}\,\)が垂直に交わるときです。点\(\,\mathrm{B}\,\)の座標は\(\,(\,0\,,\,6\,)\,\)で変わっていませんが、
関数\(\,y=a\,x^2\,\)の比例定数は\(\,①\,\)と同じではありません。

傾きが\(\,-1\,\)の直線は\(\,y\,\)切片が\(\,6\,\)なので
　\(\hspace{10pt}y=-x+6\)
また直線\(\,\mathrm{AC}\,\)は原点を通る傾き\(\,1\,\)の直線になるので
（垂直な直線なので\(\,\mathrm{△OCD}\,\)は直角二等辺三角形となる。）
　\(\hspace{10pt}y=x\)
このことから交点\(\,\mathrm{C}\,\)の座標は
（２つの直線の交点だから連立して）
　\(\hspace{10pt}\mathrm{C}:\,(\,3\,,\,3\,)\)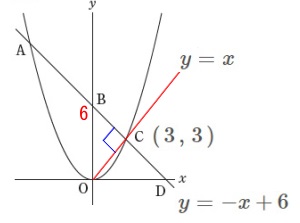さらに\(\,\mathrm{△AOC}\,\)の面積が\(\,27\,\)なので、
\(\,\mathrm{OB}\,\)が底辺、\(\,\mathrm{C}\,\)の\(\,x\,\)座標が高さとみて、
\(\,\mathrm{△OCB}\,\)の面積が\(\,9\,\)であることから
　\(\hspace{10pt}\mathrm{△OAB}=18\)
だから\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,6\,\)となります。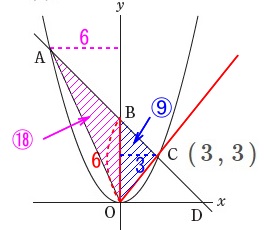点\(\,\mathrm{A}\,\)は\(\,y=-x+6\,\)上の点なので、
　\(\hspace{10pt}\mathrm{A}:(\,-6\,,\,12\,)\)
ここまでは問題の条件から出しておきましょう。
※
放物線の比例定数も出ますが必要無いのでここでは書きません。
解いていく流れからすると自分で求めているはずです。

問題はここからです。
\(\,x\,\)軸上に点\(\,\mathrm{P}\,\)をとり、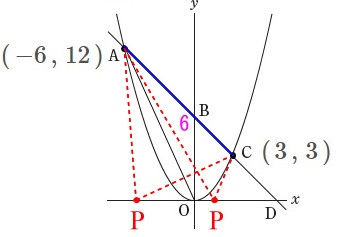\(\,\mathrm{△APC}\,\)の周の長さが最も短くなる点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。

線分\(\,\mathrm{\color{blue}{AC}}\,\)は固定されているので、
　\(\hspace{4pt}\mathrm{AP+CP}\,\)が最も短くなるとき、
ということです。

折れ線が最も短くなるというのは会員にはおなじみなので、
簡単に説明して終わりにします。

\(\hspace{4pt}\mathrm{AP+CP}\,\)が最も短くなるのは\(\,\mathrm{A\,,\,C\,,\,P}\,\)が一直線になるときですが、位置関係から３点は一直線にはならないので、
\(\,\mathrm{A}\,\)か\(\,\mathrm{C}\,\)を\(\,x\,\)軸の反対側に移します。
ここでは\(\,\mathrm{C}\,\)を移動させます。
　\(\hspace{4pt}\mathrm{C’}:(\,3\,,\,-3\,)\)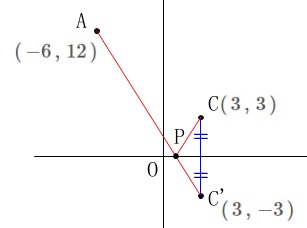線分\(\,\mathrm{CP}\,\)と線分\(\,\mathrm{C’P}\,\)は同じ長さなので、
３点\(\,\mathrm{A\,,\,P\,,\,C’}\,\)が一直線になれば良いという事ですね。

直線\(\,\mathrm{AC}\,\)の式は２点
　\(\hspace{4pt}(\,-6\,,\,12\,)\)
　\(\hspace{4pt}(\,3\,,\,-3\,)\)
を通るので、
　\(\hspace{10pt}\displaystyle y=-\frac{5}{3}\,x+2\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の方程式を求める時間はできるだけ短くしておきましょう。
変化の割合から理解しておくことがポイントです。

点\(\,\mathrm{P}\,\)は\(\,x\,\)軸上の点なので\(\,y=0\,\)だから
　\(\begin{eqnarray}\displaystyle
0&=&-\frac{5}{3}\,x+2\\
0&=&-5\,x+6\\
x&=&\underline{\underline{　\frac{6}{5}　}}
\end{eqnarray}\)

点\(\,\mathrm{A}\,\)を\(\,x\,\)の反対側に移動させて、
点\(\,\mathrm{C}\,\)と結んだ直線から求めても良いですよ。

第４問

【問４】
図形です。

【問３】同様にがっつりあるので簡単に説明します。
基本の確認と図形問題の考え方を見ておいて下さい。

\(\,\mathrm{Ⅰ}\,\)
三角形\(\,\mathrm{ABC}\,\)は１辺\(\,\mathrm{6\,cm}\,\)の正三角形です。
(1)
頂点\(\,\mathrm{A}\,\)を\(\,\mathrm{C}\,\)に重ねて折り曲げると、
三角定規ができます。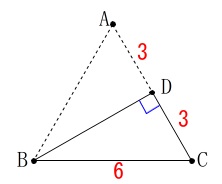よって、
　\(\hspace{10pt}\mathrm{BD}=\underline{　3\sqrt{3}　}(\,\mathrm{cm}\,)\)

(2)
今度は頂点\(\,\mathrm{A}\,\)を辺\(\,\mathrm{BC}\,\)上に折り曲げます。
※
問題の図で位置関係を確認しておいて下さい。
頂点\(\,\mathrm{A}\,\)が\(\,\mathrm{B\,,\,C}\,\)に重なるときは除外しています。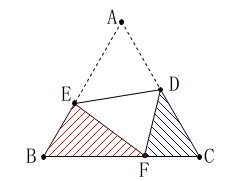このとき
　\(\,\mathrm{△EBF}\,\)　∽　\(\,\mathrm{△FCD}\,\)
を証明します。

折り返しなので等しい辺や角がありますので、
図の中に示すと分かり易いですよ。ここでは角度だけを示しておきますが、
正三角形の１角が６０°なので残りの角度に着目します。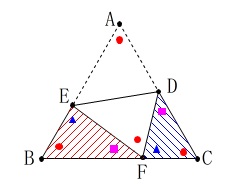三角形の内角の和から
　\(\hspace{4pt}\mathrm{\color{blue}{∠BEF}+\color{magenta}{∠BFE}}=120^{\circ}\)
（\(\hspace{4pt}\color{blue}{▲}+\color{magenta}{■}=120^{\circ}\)）
また\(\,\mathrm{∠BFC=180°}\,\)から\(\,60°\,\)引いた残りの角度から
　\(\hspace{4pt}\mathrm{\color{blue}{∠CFD}+\color{magenta}{∠BFE}}=120^{\circ}\)
このことから
　\(\hspace{4pt}\mathrm{∠BEF=∠CFD}\)
相似条件「２組の角がそれぞれ等しい。」がそろうので証明終わりです。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明の書き方は自分の書きやすい方法で構いませんよ。
（間違ったことを書いていなければ書き方に決まりはありません。）

他にも\(\,\mathrm{∠EFC=∠EBF+∠BEF}\,\)であることを利用しても良いですよ。
\(\,\mathrm{∠EBF=∠EFD=\color{red}{60^{\circ}}}\,\)なので
　\(\hspace{4pt}\mathrm{∠BEF=∠CFD}\)
を見つけるのも難しくはないでしょう。

(3)
次は図３のように折り曲げたときです。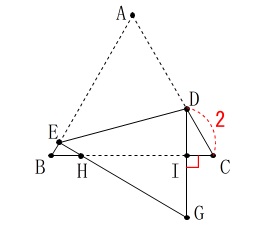長さの条件\(\,\mathrm{DC=2\,cm}\,\)、
角度の条件\(\,\mathrm{∠GIC}=90^{\circ}\)
が加わりますが、
\(\,\mathrm{△ABC}\,\)の条件は変わりません。

①
\(\,\mathrm{∠EDG}\,\)の大きさを求めます。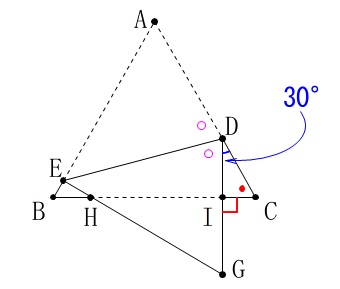折り返された角度から簡単に出ますね。

正三角形の１角なので\(\,\mathrm{∠DCI=\color{red}{●}=60°}\,\)だから
　\(\hspace{4pt}\mathrm{∠IDC}=\color{blue}{30°}\)
折り返された角度なので
　\(\hspace{4pt}\mathrm{\color{magenta}{∠ADE}=\color{magenta}{∠EDG}}\)
よって\(\,\mathrm{∠IDC}\,\)を\(\,180°\,\)から引いた残りの半分が答えとなります。
　\(\hspace{10pt}\displaystyle \mathrm{∠EDG}=\frac{150^{\circ}}{2}=\underline{　75^{\circ}　}\)

②
\(\,\mathrm{GI}\,\)の長さを求めます。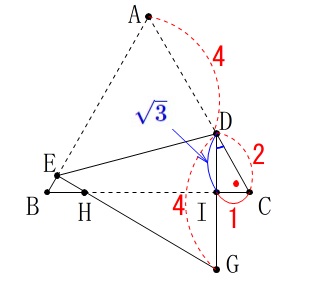素直に\(\,\mathrm{GD}\,\)から\(\,\mathrm{DI}\,\)を引けば良いです。

折り返された辺は等しいので
　\(\hspace{4pt}\mathrm{AD=\color{red}{DG}}=\color{red}{4}\)
三角定規の辺の比から
　\(\hspace{4pt}\mathrm{\color{blue}{IG}}=\color{blue}{\sqrt{3}}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{GI}&=&\mathrm{\color{red}{DG}-\color{blue}{DI}}\\
&=&\underline{　4-\sqrt{3}　}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

次いきます。

\(\,\mathrm{Ⅱ}\,\)
今度は１辺が\(\,\mathrm{6\,cm}\,\)の正方形を折り返します。
(1)
ここは方針が書いてあるので流れに乗っていきましょう。

頂点\(\,\mathrm{A}\,\)を辺\(\,\mathrm{BC}\,\)の中点\(\,\mathrm{M}\,\)に重なるように折り曲げたとき、
　\(\,\mathrm{△EBM}\,\)　∽　\(\,\mathrm{△MCH}\,\)①
\(\,\mathrm{BE}\,\)の長さを\(\,x\,\)とすると\(\,\mathrm{AE}=6-x\,\)となります。

折り曲げられた線分は等しいので、
　\(\hspace{4pt}\mathrm{EM=AE}=\color{blue}{6-x}\)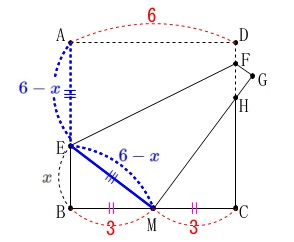直角三角形\(\,\mathrm{EBM}\,\)において三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{EM^2}&=&\mathrm{EB^2+BM^2}\\
(\color{blue}{6-x})^2&=&x^2+\color{red}{3}^2\\
x^2-12x+36&=&x^2-9\\
x&=&\underline{\underline{　\frac{9}{4}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

②
方針の順番から見ると逆に見えますが、
①はこの問題のためにあります。

相似を利用して\(\,\mathrm{HC}\,\)の長さを求めます。
　\(\,\mathrm{△EBM}\,\)　∽　\(\,\mathrm{△MCH}\,\)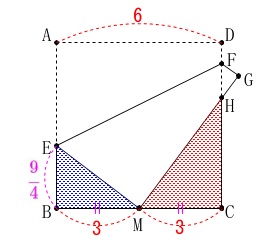①から\(\,\mathrm{BE}=\displaystyle \color{magenta}{\frac{9}{4}}\,\)だから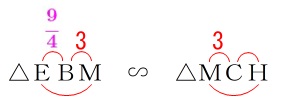
　\(\begin{eqnarray}\displaystyle
\mathrm{EB:MB}&=&\mathrm{MC:HC}\\
\frac{9}{4}:3&=&3:\mathrm{HC}\\
\frac{9}{4}\times \mathrm{HC}&=&3\times 3\\
\mathrm{HC}&=&\underline{　4　}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

方針に従えば迷うところはありません。

(2)
最終問題です。
ここが意地の見せ所となる計算が待っています。
（それほどでもないですけど。）

図５における条件は\(\,\mathrm{AB=6}\,\)は同じで
　\(\hspace{4pt}\displaystyle \mathrm{EB}=\frac{1}{4}\,\mathrm{AB}\)
　\(\hspace{4pt}\mathrm{EJ=JI}\)
なので
　\(\hspace{4pt}\displaystyle \mathrm{EB}=\frac{1}{4}\times \mathrm{AB}=\frac{1}{4}\times 6=\color{red}{\frac{3}{2}}\)
このとき
　\(\hspace{4pt}\displaystyle \mathrm{AE}=\mathrm{AB-EB}=6-\frac{3}{2}=\color{blue}{\frac{9}{2}}\)
また、
　\(\hspace{4pt}\displaystyle \mathrm{EJ=JI}=\frac{1}{2}\times \frac{9}{2}=\color{magenta}{\frac{9}{4}}\)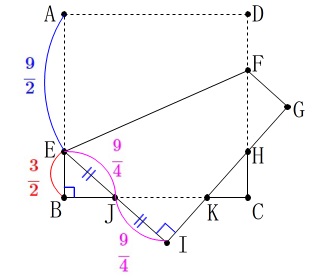求めるのは４点\(\,\mathrm{E\,,\,B\,,\,I\,,\,K}\,\)を通る円の直径ですが、
円周角の定理から\(\,\mathrm{EK}\,\)の長さになります。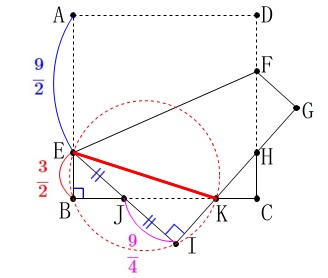相似と三平方の定理から求めます。
利用する直角三角形で人によって分かれると思いますが、
どうでも良いです。

あれこれ考える前に先ずは分かる線分を求めておきましょうか。
（ここまで来れば相似や三平方の定理における計算はできるという前提で省略します。）
\(\,\mathrm{△EBJ}\,\)において三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{EJ^2}&=&\mathrm{EB^2+BJ^2}\\
\left(\,\color{magenta}{\frac{9}{4}}\,\right)^2&=&\left(\,\color{red}{\frac{3}{2}}\,\right)^2+\mathrm{BJ^2}\\
\end{eqnarray}\)
この関係から
　\(\hspace{4pt}\displaystyle \mathrm{BJ}=\frac{3\sqrt{5}}{4}\)
また、
　\(\,\mathrm{△EBJ}\,\)　∽　\(\,\mathrm{△KIJ}\,\)
なので
　\(\hspace{4pt}\displaystyle \mathrm{JK}=\frac{27\sqrt{5}}{20}\)
および
　\(\hspace{4pt}\displaystyle \mathrm{IK}=\frac{9\sqrt{5}}{10}\)
ここまでが数学の基本を利用しまくるところです。
両方出す必要はありませんが、どちらかは出しておきましょう。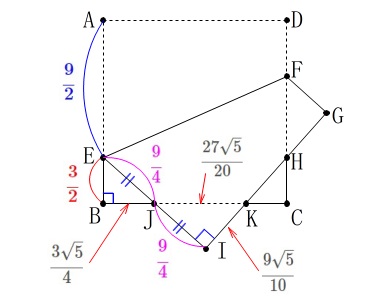後は\(\,\mathrm{△EBK}\,\)を使うか\(\,\mathrm{△EIK}\,\)を使うかです。
いずれにしても三平方の定理から求まります。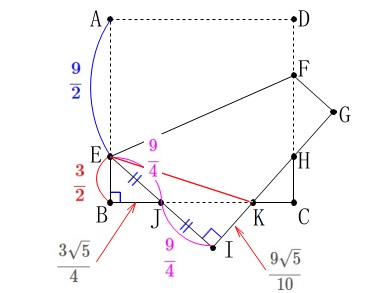数値が小さく見える\(\,\mathrm{△EIK}\,\)を使うことにします。笑
　\(\begin{eqnarray}\displaystyle
\mathrm{EK^2}&=&\mathrm{EI^2+IK^2}\\
&=&\left(\,\frac{9}{2}\,\right)^2+\left(\,\frac{9\sqrt{5}}{10}\,\right)^2\\
&=&\frac{81}{4}+\frac{405}{100}\\
&=&\frac{81}{4}+\frac{81}{20}\\
&=&\frac{81\times 5+81}{20}\\
&=&\frac{405+81}{20}\\
&=&\frac{486}{20}\\
&=&\frac{243}{10}
\end{eqnarray}\)
（計算ミスしそうなのでここはていねいに計算しました。）
これから
　\(\begin{eqnarray}\displaystyle
\mathrm{EK}&=&\frac{\sqrt{243}}{\sqrt{10}}\\
&=&\underline{\underline{　\frac{9\sqrt{30}}{10}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)