２０２３年（令和５年）度愛知県公立高校入試数学の問題と解説

２０２３年（令和５年）度愛知県公立高校入試数学の問題と解説です。
入試制度がかなり変わった年なので気をつけておきたいところだったのですが、
基本重視の受験生思いの問題構成でした。
解説は一通りしておきますが問題を解くことより気をつけたいこともあるので、
簡単にですがお伝えしておきます。

２０２３年（令和５年）度愛知県公立高校入試数学の問題

大問３問の問題構成は変わっていません。

⇒　２０２３年（令和５年）度愛知県公立高校入試数学の問題ＰＤＦ

ただし、形式が変わっているので確認しておきましょう。
受験生は問題の１，２ページ目の「注意」は事前に何度も見ておくと良いです。
慣れは重要な部分なので必ずです。
ここは対策ページではないのですが、
ちょっとした対策も後で書いておきますので参考にして下さい。

２０２３年（令和５年）度愛知県公立高校入試数学の解説

愛知県から通知されていますし、
受験生は当然知っていることですが、
「令和5年度入学者選抜から、一般選抜で2校に志願した場合でも学力検査は1回としました。」
とあるように試験は１回です。
（\(\,\mathrm{A\,,\,B}\,\)日程があったので令和4年までは2回試験がありました。）

もう一つ、愛知県でもマーク式を採用しています。
こういった変化のある年は受験生の混乱があるのですが、
それを見越してか、この年はかなり受験生に優しい問題です。

対策ではありませんが「マーク式だから勘で」という甘い考えは捨てておきましょう。
逆に自分の解答を疑いたくなるような答えの選択を迫られることになるので、
自信を持てるようにしっかり基礎は仕上げておく必要がありますよ。

解説は会員向けになるかもしれませんが細かくはしません。
『基本レポート』で十分ですので何度も読んでおいて下さい。

第１問

\(\,\large{1}\,\)
(1)
　\(\hspace{10pt}6-(-4)\div 2\\
=6-(-2)\\
=\underline{　8　}\)

計算順序を間違えないようにしましょう。
掛け算割り算部分が先です。
(2)
　\(\hspace{10pt}\displaystyle \frac{3x-2}{6}-\frac{2x-3}{9}\\
\displaystyle =\frac{3(3x-2)-2(2x-3)}{18}\\
\displaystyle =\frac{9x-6-4x+6}{18}\\
\displaystyle =\underline{\underline{　\frac{5x}{18}　}}\)

答えは\(\displaystyle \,\frac{5}{18}\,x\,\)を選びますが、
分数計算はいつも通りです。
(3)
　\(\hspace{10pt}\displaystyle 6x^2\div (-3xy)^2\times 27xy^2\\
\displaystyle =\frac{6x^2\times 27xy^2}{(-3xy)^2}\\
\displaystyle =\frac{6x^2\times 27xy^2}{9x^2y^2}\\
\displaystyle =\underline{　18x　}\)

割り算部分は分母に回すのもいつも通りです。
（２行目はなくても良いです。）

(4)
　\(\hspace{10pt}(\sqrt{5}-\sqrt{2})(\color{red}{\sqrt{20}+\sqrt{8}})\\
=(\sqrt{5}-\sqrt{2})(\color{red}{2\sqrt{5}+2\sqrt{2}})\\
=2\color{blue}{(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})}\\
=2\color{blue}{(5-2)}\\
=\underline{　6　}\)

無理数計算は慣れによって暗算程度が変わります。
割り算を除いてできるだけルートの中を簡単にしておいた方が、
数値が小さくなるのでミスは減ります。
途中で計算公式
　\(\hspace{4pt}\color{blue}{(a+b)(a-b)=a^2-b^2}\)
を使っています。
計算公式は無理数でも関係なく使えるので覚えておきましょう。

もちろんそのまま計算しても結果は同じですよ。
　\(\hspace{10pt}(\sqrt{5}-\sqrt{2})(\color{red}{\sqrt{20}+\sqrt{8}})\\
=\sqrt{100}+\sqrt{40}-\sqrt{40}-\sqrt{16}\\
=10-4=\underline{　6　}\)

(5)
きれいな解法があるのか？
などと考えるヒマがあるなら強引にでも展開した方が早い場合が多いです。
　\(\begin{eqnarray}\displaystyle
(x-3)^2&=&-x+15\\
x^2-6x+9&=&-x+15\\
x^2-5x-6&=&0\\
(x+1)(x-6)&=&0\\
x&=&\underline{　-1\,,\,6　}
\end{eqnarray}\)

程度によりますが明らかに「まとまり」とできる部分がある場合を除いて、
まとまりをつくってエレガントに、なんて考えなくて良いです。

⇒　中学3年の因数分解公式まとめと典型的な応用問題の解き方

因数分解できる事は前提として２次方程式の問題はあります。

(6)
「１つ」選べば良いので適当に探しても良いですが、
ここではすべて関数にしておきます。
ア　\(\hspace{10pt}\displaystyle xy=100　または　y=\frac{100}{x}\)
イ　\(\hspace{10pt}\displaystyle \underline{　\color{red}{y=3\,x}　}\)
ウ　\(\hspace{10pt}\displaystyle y=\pi\,x^2\)
エ　\(\hspace{10pt}\displaystyle y=x^3\)

イは比例とも言いますが一次関数です。
(7)
\(\,1\,\)が２枚あるので区別して樹形図です。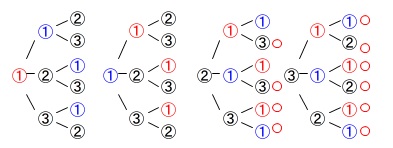続けて取り出すので同じ数字は並びません。
　\(\hspace{10pt}\displaystyle \frac{10}{24}=\underline{\underline{　\frac{5}{12}　}}\)

余事象（\(\,213\,\)より小さい）を考えたくなりますが素直に樹形図です。
(8)
「１つ」選ぶので反例がでないものを選んでも良いです。
アの反例：\(\,\color{red}{4}-2\,=\,2\)
ウの反例：\(\,3\times \color{red}{2}=6\)
エの反例：\(\,\color{red}{3}^2-1\,=\,8\)

イに反例はありません。
　\(\hspace{10pt}\color{red}{4\,n}+\color{blue}{5}=(\,\color{red}{偶数}\,)+(\,\color{blue}{奇数}\,)\)
なので\(\,n\,\)がどんな整数であっても奇数です。

(9)
一次関数の変化の割合は「傾き」です。
　\(\hspace{4pt}\displaystyle (\,変化の割合\,)=\frac{　(\,y\,の増分\,)　}{　(\,x\,の増分\,)　}\)
関数\(\displaystyle \,y=2\,x^2\,\)の変化の割合を求めれば良いですね。
　\(\hspace{4pt}(\,x\,の増分\,)=\,3-1\,=\,\color{red}{2}\)
　\(\hspace{4pt}(\,y\,の増分\,)=\,2\times 3^2-2\times 1^2\,=\,\color{blue}{16}\)
なので
　\(\hspace{4pt}\displaystyle (\,変化の割合\,)=\frac{\color{blue}{16}}{\color{red}{2}}=\underline{　8　}\)
この傾きを持つのは、
　\(\,\underline{　エ　}　y=8\,x+6\,\)
(10)
「全て」選ぶので全てを見ていきます。
ア
異なる２点を含むのは１つの直線を含むのと同じです。
エ
同じ直線上にある３点を含む、というのはアと同じです。直線\(\,\ell\,\)を軸にクルクル回せばいくらでもあります。
イ
交わる２直線を含む平面は定まります。
ウ
平行な２直線を含む平面は定まります。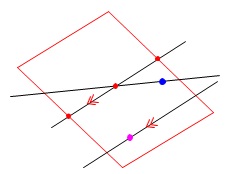平面は一直線上にない３点があれば定まります。
イもウも１つの直線以外に１点選べるので定まりますね。
答え　\(\underline{　イ　\,,\,　ウ　}\)

第２問

\(\,\large{2}\,\)
(1)
データの用語の意味と箱ひげ図の読み取りです。
「２つ」選ぶので怪しいものではなく確実にいえることを探すと早いかも。
ア
「範囲」は最大値と最小値の差なので違います。×
イ
四分位範囲は第３四分位数と第１四分位数の差なので同じ値です。○
ウ
中央値は第２四分位なので同じ値です。○
答えは出ましたが一応説明を続けます。
エ
第三四分位数に着目すると\(\,\mathrm{B}\,\)組の方が多いです。×
（四分位数は度数で区切られることを忘れないように。）
オ
中央値となる\(\,\mathrm{25\,m}\,\)に数人いても箱ひげ図は変わらないので同じとは言えない。×
答え\(\hspace{10pt}\underline{　イ　,　ウ　}\)
(2)
合同の証明です。
　\(\,\mathrm{△ABC}\,\)≡\(\,\mathrm{△EAD}\,\)
平行四辺形\(\,\mathrm{ABCD}\,\)に\(\,\mathrm{AB=AE}\,\)の条件があります。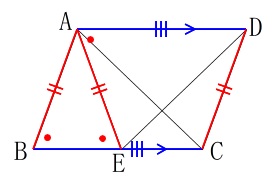証明は図の中で終わらせておきましょう。
二等辺三角形の底角は等しいから
　\(\hspace{10pt}\mathrm{∠ABC}=\mathrm{\underline{　\color{red}{∠AEB}　}}　･･･③\)
平行線の錯角等しいから
　\(\hspace{10pt}\mathrm{\color{red}{∠AEB}}=\mathrm{\underline{　∠EAD　}}　･･･④\)
③④から
　\(\hspace{10pt}\mathrm{∠ABC}=\mathrm{∠EAD}　･･･⑤\)　
後は平行四辺形の対辺が等しいことと仮定の\(\,\mathrm{AB=AE}\,\)から、
「２組の辺とその間の角がそれぞれ等しい。」
という合同条件がそろいます。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

ここでは選択肢から選ぶので記号の順序も気にしなくて良いですが、
合同も相似も証明のポイントは変わりません。

(3)
動点問題で２点が逆方向に違う速さで動きます。
動点問題はいつも通り変化のある点を見ていけば良いです。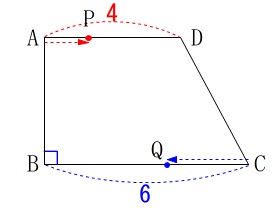動き始めは分かり易いと思います。
ただ、点\(\,\mathrm{Q}\,\)の動きを\(\,x\,,\,y\,\)の関数とみると利用がややこしいです。
①
\(\,x=6\,\)、つまり\(\,6\,\)秒後に\(\,\mathrm{AP}\,\)の長さは？ということです。
\(\,4\,\)秒後に一度折り返すので、折り返して\(\,2\,\)秒後です。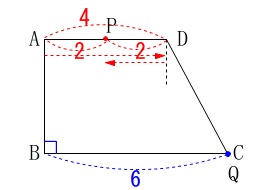点\(\,\mathrm{P}\,\)だけ見ておけば良いですよ。
点\(\,\mathrm{P}\,\)は\(\,\mathrm{D}\,\)から\(\,2\,\)だけ\(\,\mathrm{A}\,\)の方向に動くので
　\(\hspace{10pt}\mathrm{AP}=\underline{　y=2　}\)

このとき点\(\,\mathrm{Q}\,\)は\(\,\mathrm{C}\,\)に戻っていることも見ておくと次が楽になります。
②
問題の意味は\(\,\mathrm{AP}\,\)と\(\,\mathrm{BQ}\,\)が等しくなるのは何回か？です。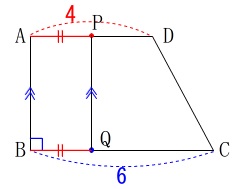\(\,\mathrm{BP}\,\)を\(\,y\,\)として関数にしても良いですが、
グラフを利用するように問題が言ってくれているのでグラフを完成させましょう。
\(\,y\,\)が等しいときなので点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)のグラフの交点の数を求めます。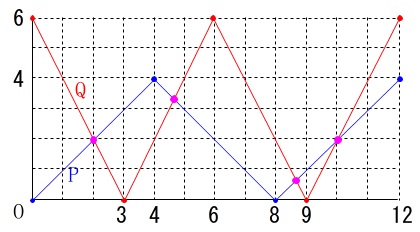点\(\,\mathrm{P}\,\)は\(\,4\,\)秒毎に、点\(\,\mathrm{Q}\,\)は\(\,3\,\)秒毎に折り返すことが分かれば、
直線の繰り返しなので交点の数が求まります。
　\(\hspace{10pt}\underline{　エ　4\,回　}\)

点\(\,\mathrm{P}\,\)の関数を３つ（直線なので一次関数です。）、
点\(\,\mathrm{Q}\,\)の関数を４つ求めても良いですが、
交点となる\(\,x\,,\,y\,\)は求めていないので見た目で判断して良いでしょう。

第３問

\(\,\large{3}\,\)
図形一色ですね。
数値を入れるのでマークシートだからといってここからは勘には頼れません。
(1)
角度を求めます。
条件：
　\(\,\mathrm{AO}\,\)∥\(\,\mathrm{BC}\,\)
　\(\hspace{4pt}\mathrm{∠AOB}=48^{\circ}\)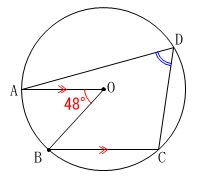求める角度が弧\(\,\mathrm{ABC}\,\)の円周角だから、
中心角\(\,\mathrm{∠AOC}\,\)が知りたいですね。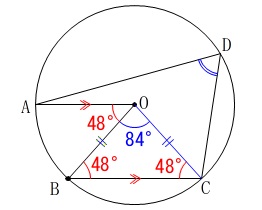半径が等しいことから\(\,\mathrm{△OBC}\,\)は二等辺三角形で、
底角が等しくなるから
　\(\hspace{4pt}\mathrm{∠OBC=∠OCB}=\color{red}{48°}\)
頂角が
　\(\hspace{4pt}\mathrm{∠BOC}=\color{blue}{84°}\)
中心角となる\(\,\mathrm{∠AOC}\,\)は
　\(\hspace{10pt}\mathrm{∠AOC}=\color{red}{48°}+\color{blue}{84°}=132°\)
よって求める角は
　\(\hspace{10pt}\displaystyle \mathrm{∠ADC}=\frac{1}{2}\times 132°=\underline{　66°　}\)

円周角の和として求めても良いです。
　\(\hspace{10pt}\mathrm{∠ADB}=24°\)
　\(\hspace{10pt}\mathrm{∠BDC}=22°\)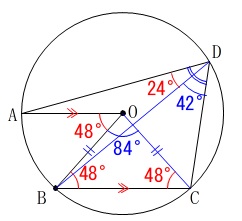または
二等辺三角形\(\,\mathrm{OAB}\,\)から底角を求めて、
　\(\hspace{10pt}\mathrm{∠OBA}=66°\)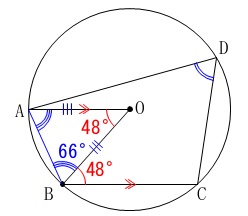円に内接する四角形なので、
内対角の和が\(\,180°\,\)になることから
　\(\begin{eqnarray}
\mathrm{∠ADC}&=&180°-\mathrm{∠ABC}\\
&=&180°-(66°+48°)\\
&=&180°-114°\\
&=&\underline{　66°　}
\end{eqnarray}\)
補助線引いて分かる角度を書き込んで行けば何でも良いです。

(2)
長方形内の線分と面積で平行四辺形と考え方は同じです。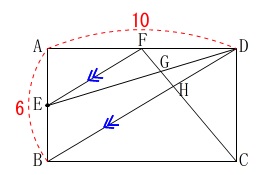平行四辺形の条件だけだと面積に苦労しそうですが、
長方形なのでいろいろと使えるのでなんとかなりそうです。
①
線分\(\,\mathrm{FE}\,\)の長さです。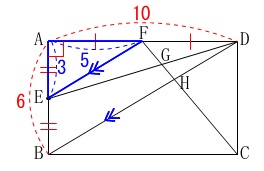中点連結定理から\(\,\mathrm{F}\,\)は\(\,\mathrm{AD}\,\)の中点になるので、
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{FE^2}&=&\mathrm{AE^2+AF^2}\\
&=&3^2+5^2\\
&=&34\\
\mathrm{FE}&=&\pm \sqrt{34}
\end{eqnarray}\)
長さだから正の数で
　\(\hspace{10pt}\mathrm{FE}=\underline{　\sqrt{34}　(\,\mathrm{cm}\,)}\)

２つの定理の確認でした。

②
三角形\(\,\mathrm{DGH}\,\)の面積です。見やすくしているだけで(1)までの条件はそのままです。

底辺と高さとなる垂線は見つからないし、
相似を利用して線分比でいきましょう。
※
（どうでも良いけど\(\,\mathrm{BD}\,\)と\(\,\mathrm{FC}\,\)は直交していませんよ。）

といっても方向性はいくつもあります。

１つだけ共通して出しておきたい比があります。
　\(\hspace{4pt}\mathrm{\color{red}{FG}:\color{blue}{GH}:\color{magenta}{HC}}\)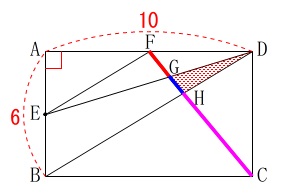これが分かれば面積は長方形から直接出てきます。
（お決まり問題だから会員は軽く終わっていると思います。）

この線分比は後で求めておきますが、
分かる比から書き込んで答えを出しておきましょう。
　\(\,\mathrm{△HDF}\,\)∽\(\,\mathrm{△HBC}\,\)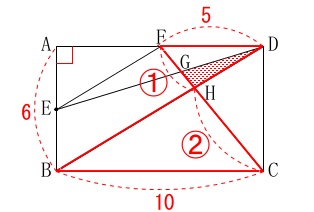相似比は
　\(\hspace{4pt}\mathrm{FD:CB=FH:CH}=\color{red}{①}:\color{red}{②}\)

次は\(\,\mathrm{FG:GH}\,\)が知りたいので相似を探すと、
（\(\,\mathrm{DE}\,\)を延長しても良いのですが）
補助線なしだと
　\(\,\mathrm{△GEF}\,\)∽\(\,\mathrm{△GDH}\,\)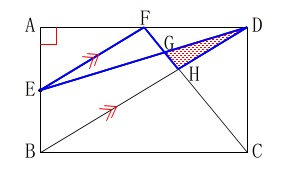このとき前に出てきた相似比と中点連結定理から
　\(\hspace{4pt}\displaystyle \mathrm{FE}=\frac{1}{2}\times \mathrm{BD}\)
　\(\hspace{4pt}\displaystyle \mathrm{DH}=\frac{1}{3}\times \mathrm{BD}\)
なので
　\(\hspace{10pt}\displaystyle \mathrm{FE:DH}=\frac{1}{2}:\frac{1}{3}\,=\,\color{blue}{③}:\color{blue}{②}\)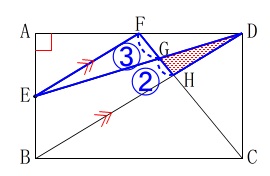ここからは具体的な面積でも求める事ができます。
先に比から計算すると
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGH}&=&\frac{2}{5}\times \mathrm{\color{blue}{△HFD}}\\
&=&\frac{2}{5}\times \color{blue}{\frac{1}{3}\times \mathrm{△FDC}}\\
&=&\frac{2}{5}\times \frac{1}{3}\times \frac{1}{4}\times \color{red}{6\times 10}\\
&=&\underline{　2　}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

\(\,\mathrm{△FDC}\,\)の面積は長方形の\(\,\displaystyle \frac{1}{4}\,\)です。
※
いってなかった？長さの単位は\(\,\mathrm{cm}\,\)です。

具体的な面積で計算すると
　\(\begin{eqnarray}\displaystyle
\,\mathrm{\color{red}{△FDC}}\,&=&\frac{1}{2}\times 5\times 6\\
&=&15
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△HFD}}&=&\frac{1}{1+2}\times \mathrm{\color{red}{△FDC}}\\
&=&\frac{1}{3}\times 15\\
&=&5
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGH}&=&\frac{2}{3+2}\times \mathrm{\color{blue}{△HFD}}\\
&=&\frac{2}{5}\times 5\\
&=&\underline{　2　}(\,\mathrm{cm^2}\,
\end{eqnarray}\)

面積計算は長方形の\(\,60\,\)から図の中で追っていけば分かり易いです。
　\(\hspace{4pt}\displaystyle \mathrm{△DGH}=60\times \frac{1}{4}\times \frac{1}{3}\times \frac{2}{5}　･･･☆\)

知りたかった線分比を求めておきましょう。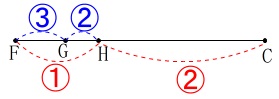\(\,\mathrm{FC}\,\)の長さは具体的にありますが、
仮に\(\,\mathrm{FC}=\color{magenta}{15}\,\)とします。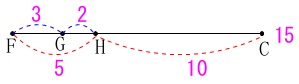知りたかった線分比は
　\(\hspace{10pt}\mathrm{\color{red}{FG}:\color{blue}{GH}:\color{magenta}{HC}}=\color{red}{3}:\color{blue}{2}:\color{magenta}{10}\)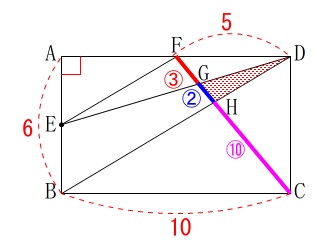このお決まりの線分比がでていればどうとでもなるでしょう。

ところで、\(\,\mathrm{DE}\,\)を延長した人もいると思います。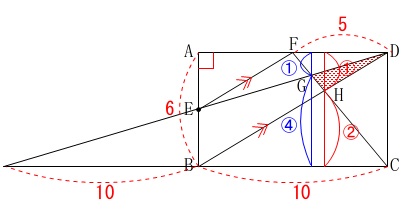線分比は何らかの方法で求めてあることにして、
（具体的な数値で計算すると）
　\(\begin{eqnarray}\mathrm{\color{blue}{△HFD}}&=&\frac{1}{2}\times 5\times \color{red}{\frac{1}{1+2}\times \mathrm{AB}}\\
&=&\frac{1}{2}\times 5\times \color{red}{\frac{1}{3}\times 6}\,\\
&=&\,\color{blue}{5}
\end{eqnarray}\)
　\(\begin{eqnarray}\mathrm{\color{magenta}{△GFD}}&=&\frac{1}{2}\times 5\times \color{blue}{\frac{1}{1+4}\times \mathrm{AB}}\\
&=&\frac{1}{2}\times 5\times \color{blue}{\frac{1}{5}\times 6}\\
&=&\color{magenta}{3}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGH}&=&\mathrm{\color{blue}{△HFD}}-\mathrm{\color{magenta}{△GFD}}\\
&=&5-3\,=\,2
\end{eqnarray}\)

長方形なので線分比が出れば全ての部分面積は求まりますが、
具体的な面積計算では平行四辺形の場合を考えるとお勧めしません。

ちなみに、線分比がある程度でた時点で答えを出した人は良くカードを見ていますね。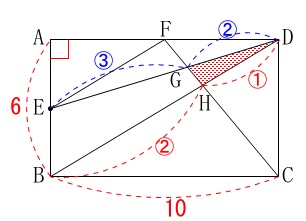\(\,\mathrm{△DEB}\,\)が具体的に求まるので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGH}&=&\color{blue}{\frac{2}{2+3}}\times \color{red}{\frac{1}{1+2}}\times \mathrm{\color{magenta}{△DEB}}\\
&=&\color{blue}{\frac{2}{5}}\times \color{red}{\frac{1}{3}}\times \color{magenta}{\frac{1}{2}\times 3\times 10}\\
&=&2
\end{eqnarray}\)

なんだか自分で見てもまとまりが良くないです。
線分比を求める方向で進めてください。
（こういう方向性が多いときは考え方は１つだけにした方が良いですね。）

私が答えを出した計算方法は線分比を出す方針で突き進んで上の☆です。

(3)
立体（空間図形）での面積と体積です。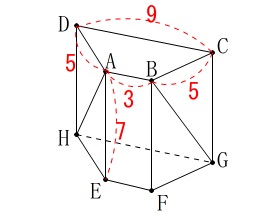きれいな数値でややこしくもないので簡単に済ませます。
※
長さの単位は\(\,\mathrm{cmで}\,\)す。
①
台形\(\,\mathrm{ABCD}\,\)の面積です。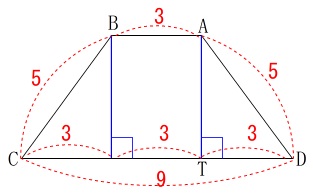台形の面積を求める公式は小学校で習っているので説明は不要でしょう。

高さとなる\(\,\mathrm{AT}\,\)が必要です。
等脚台形なので直角三角形\(\,\mathrm{ATD}\,\)において三平方の定理を利用して
　\(\begin{eqnarray}
\mathrm{AT^2+TD^2}&=&\mathrm{AD^2}\\
\mathrm{AT^2}+3^2&=&5^2\\
\mathrm{AT^2}&=&16\\
\mathrm{AT}&=&\pm 4
\end{eqnarray}\)
長さなので正の数だから
　\(\hspace{10pt}\mathrm{AT}=\color{blue}{4}\)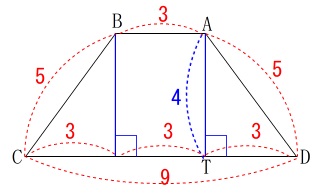よって、求める台形の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{\color{red}{3}+\color{red}{9}}{2}\times \color{blue}{4}\\
&=&\underline{　24　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)
②
公式のない立体の体積です。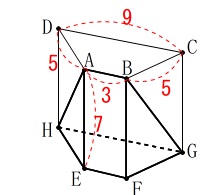いつも通り全体と部分がありますが、
『部分』＋『部分』で良いでしょう。
①で引いた垂線（台形の高さ）を含む平面で立体を台形と垂直に切ります。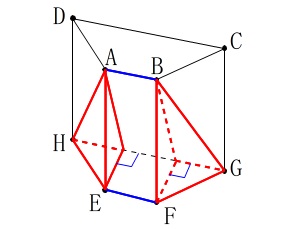２つの三角すいと１つの三角柱を加えれば、
求める体積\(\,V\,\)が求まります。
長さは①で求めてあるので確認しながら計算しましょう。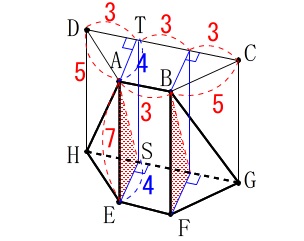これがわかりにくいという人は、
自分で図に書き込んでいないからです。
人の解答見て分かった気になっているだけでは答えは出ません。
きれいな数値で取り組みやすくしてくれているとはいえ、
愛知県はそこまで甘くはないです。

三角柱の体積\(\,V_1\,\)は底面\(\,\mathrm{△AES}\,\)、高さ\(\,3\,\)なので
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{2}\times 7\times 4\times 3\\
&=&42
\end{eqnarray}\)

２つの三角すいは体積は同じです。
底面を\(\,\mathrm{△AES}\,\)高さを\(\,\mathrm{HS}\,\)としているので、
片方の三角すいの体積を\(\,V_2\,\)とすると
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \frac{1}{2}\times 7\times 4\times 3\\
&=&14
\end{eqnarray}\)
よって、求める体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&V_1+2\times V_2\\
&=&42+2\times 14\\
&=&\underline{　70　}\,(\mathrm{cm^3}\,)
\end{eqnarray}\)

底面積が同じだから求める体積\(\,V\,\)は三角すいの体積\(\,V_2\,\)５つ分だから
　\(\begin{eqnarray}
V&=&5\times V_2\\
&=&5\times 14\\
&=&70
\end{eqnarray}\)
でも良いですが『部分』＋『部分』で見ているので足します。

自分で計算してみて下さい。
大した計算ではないから短時間で出てくると思いますよ。

以上です。

変化の年だからでしょうか、マークする時間を考えてくれ、
きれいな数値で問うてくる優しい問題でした。
ただし、頭の中だけで処理できるとは思えないので、
しっかり手は動かし続ける必要はあります。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

形式が変わったからといって過去問に意味がないわけではありません。
内容は変わらず、と見ていても良いです。
過去問は\(\,\mathrm{A\,,\,B}\,\)と日程２つ分あるので参考になるところは多いと思いますよ。

マークシート形式の問題に慣れたいなら、
当会で解説している都道府県では東京都、神奈川県が参考になります。

⇒　全国の公立高校入試 数学過去問の解答解説

問題の構成は多少違いますが問われる内容は同じ数学です。