２０２３年（令和５年）度広島県公立高校入試の数学の問題と解説

２０２３年（令和５年）度広島県公立高校入試の数学の問題と解説です。
問題は大問で６つあります。
構成は基本から標準までなので、
基本をしっかりおさせておけば時間には余裕が持てると思います。
解説は簡単に済ませておきますので解答の流れだけでも確認しておいて下さい。

２０２３年（令和５年）度広島県公立高校入試の数学の問題

問題数も例年とそれ程変わりありません。

⇒　令和５年度広島県公立高校入試の数学の問題

広島県が公開してくれている\(\,\mathrm{PDF}\,\)ですが問題が２ページ分まとまっています。
それでも計算スペースはなんとかなるのでしっかり埋め尽くして下さい。

２０２３年（令和５年）度広島県公立高校入試の数学の解説

解いていくだけなので解説になるかわかりませんが、
問題の条件を見て、自分で確認しながら進めてください。
※
説明するまでもないというわけではありません。
広島県はブレずに基本重視だと過去数年分見て頂ければ分かります。
（それでも、、、という場合はご質問ください。加筆します。）

第１問

\(\color{black}{\fbox{1}}\)
(1)
\(\hspace{10pt}-8-(-2)+3\\
=-8+2+3\\
=\underline{　-3　}\)
(2)
\(\hspace{10pt}\displaystyle 28x^2\div 7x\\
\displaystyle =\frac{28x^2}{7x}\\
=\underline{　4x　}\)
(3)
\(\hspace{10pt}\displaystyle \sqrt{50}-\frac{6}{\sqrt{2}}\\
\displaystyle =5\sqrt{2}-\frac{6\sqrt{2}}{2}\\
=5\sqrt{2}-3\sqrt{2}\\
=\underline{　2\sqrt{2}　}\)
※
暗算してミスするより素因数分解、分母の有理化を確実にしましょう。
(4)
\(\hspace{10pt}(x-6y)^2\\
=\underline{　x^2-12xy+36y^2　}\)

展開公式は覚えておいた方が後々役に立ちます。

⇒　中学3年の乗法展開公式や因数分解と計算を楽にする利用方法

展開なので地道にしても必ず答えはでますが、
いつまでも算数していても限界が出てきますよ。

(5)
２次方程式を解きます。
\(\hspace{10pt}x^2+3x-5\,=\,0\)
左辺が因数分解できないので解の公式を利用します。
\(\begin{eqnarray}
x&=&\frac{-3\pm \sqrt{3^2-4\cdot 1\cdot (-5)}}{2\cdot 1}\\
&=&\frac{-3\pm \sqrt{9+20}}{2}\\
&=&\underline{\underline{　\frac{-3\pm \sqrt{29}}{2}　}}
\end{eqnarray}\)
※
「\(\,\cdot\,\)」は掛け算の意味です。
(6)
反比例のグラフ上での格子点の数です。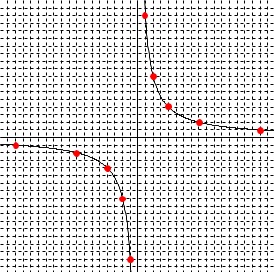\(\,y\,\)が整数になるのは\(\,x\,\)が比例定数\(\,16\,\)の約数のときで、
\(\hspace{10pt}x=\pm 16\,,\,\pm 8\,,\,\pm 4\,,\,\pm 2\,,\,\pm 1\)
原点対象なので第１象限と第３象限に同数あるとこを忘れずに。
答え　\(\hspace{10pt}\underline{　10　}個\)
※
細かい線は必要ありませんが、
グラフは簡単にでも描いて考える方が分かり易いです。

(7)
底面は対角線が\(\,4\,\mathrm{cm}\,\)の正方形なので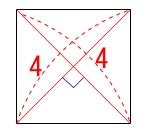求める体積\(\,V\,\)は
\(\begin{eqnarray}
V&=&\frac{1}{3}\times \frac{1}{2}\times 4\times 4\times 6\\
&=&\underline{　16　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)
(8)
四分位範囲は第３四分位数と第３四分位数との差なので、
最も大きいのは\(\,\mathrm{C}\,\)市です。
答え　\(\,\underline{　ウ　}\,\)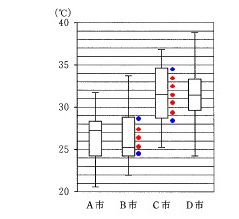おおまかな見た目でも良いですが、
確実に含む階級の数で読み取るとはっきりします。

第２問

\(\color{black}{\fbox{2}}\)
(1)
先ずは比例定数を求めに行きます。
\(\hspace{10pt}\displaystyle y=a\,x^2\)
点\(\,\mathrm{A\,(\,3\,,\,5\,)}\,\)を通るので
\(\begin{eqnarray}
5&=&a\times (\,3\,)^2\\
a&=&\frac{5}{9}
\end{eqnarray}\)
関数は決まりました。
\(\hspace{10pt}\displaystyle y=\frac{5}{9}\,x^2\)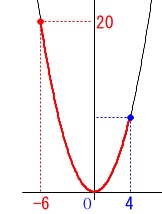最大値は\(\,x=-6\,\)のときの\(\,y=20\,\)で、
最小値は\(\,x=0\,\)のときの\(\,y=0\,\)です。
\(\hspace{10pt}\underline{　0\,≦\,y\,≦\,20　}\)

\(\,x=4\,\)のときは最大最小には関係ありません。
本来自分でやるべきなのに、
折角グラフの概形を与えてくれているのだから利用しましょう。

(2)
相対度数分布表があります。
印刷ミスか？と思ったら問題になっていました。

求めるのは、「階級値」ですね。
普通なら消えているのが１つの累積相対度数から見ていくと思います。
\(\,60\,\)以上\(\,120\,\)未満の階級の度数が\(\,11\,\)で、
累積度数は\(\,15\,\)になるので累積相対度数は
\(\hspace{10pt}\displaystyle \frac{15}{50}=0.30\)
（ここはなくても良いのですが一応流れ的に示しておきました。）
累積相対度数は全て分かったので累積度数から度数が分かります。
（相対度数は必要無いので省きます。）
\(\begin{array}{|c|c|c|c|} \hline
階級　&　度数　&　累積度数　&　累積相対度数　\\ \hline
0～60 & 4 & 4 & 0.08 \\ \hline
60～120 & 11 & 15 & 0.30 \\ \hline
120～180 & 13 & \color{red}{28} & \color{red}{0.56} \\ \hline
180～240 & 10 & \color{blue}{38} & \color{blue}{0.76} \\ \hline
240～300 & 5 & 43 & 0.86 \\ \hline
\,300～360\, & 7 & 50 & 1.00 \\ \hline
\end{array}\)
累積度数の差がそれぞれの階級の度数になります。
最も度数の多い階級の階級値は
\(\hspace{10pt}\underline{　150　}\,(\,分\,)\)

累積相対度数に度数合計\(\,50\,\)をかけると累積度数を求める事ができるので、
累積相対度数だけから累積度数を埋めて度数を出すのが最短ですが、
表を埋めることを目的に進めて良いです。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

階級値はその階級の中央値です。

(3)
２桁の自然数なので\(\,a\,\)は\(\,0\,\)ではありません。

「十の位の数を\(\,a\,\)、一の位の数を\(\,b\,\)とすると
もとの２桁の自然数は\(\,10a+b\,\)、
十の位の数と一の位の数を入れかえた数は\(\,10b+a\,\)と表される。
もとの数を\(\,4\,\)倍した数と、入れかえた自然数を\(\,5\,\)倍した数の和は
\(\hspace{10pt}4(10a+b)+5(10b+a)\\
=40a+4b+50b+5a\\
=45a+54b\\
=9(5a+6b)\)
\(\,5a+6b\,\)は自然数なのでこれは\(\,9\,\)の倍数である。
よって、、、」
とでもまとめておけば良いです。
※
「自然数」でも「整数」でも倍数であることはいえます。
入れかえた数が２桁かどうかに関わらず、
\(\,5a+6b\,\)が負の数になることはないので自然数で良いですよ。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

いろいろな数を文字を使って表せることは必須です。

第３問

\(\color{black}{\fbox{3}}\)
平行四辺形です。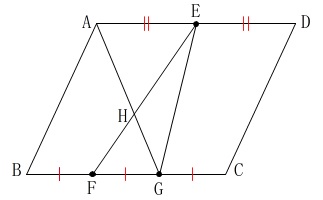具体的な長さの条件はありませんが、
各点の条件は問題から読み取っておきましょう。
(1)
角度を求めます。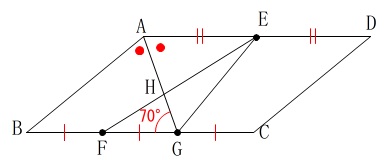実際の試験場では角度は適当で良いです。
（問題に与えられた図の中で処理して良い。）
平行線の錯角が等しくなる事から
\(\hspace{10pt}\mathrm{∠DAG=∠AGB=∠BAG}=\color{red}{70°}\)
三角形の内角の和から
\(\hspace{10pt}\mathrm{∠ABC}=\color{blue}{40°}\)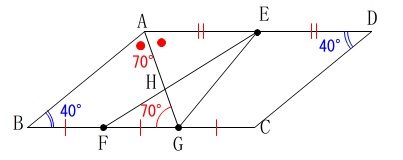平行四辺形の対角は等しいので
\(\hspace{10pt}\mathrm{∠ADC}=\underline{　40　}°\)
(2)
線分比が関係するのはここからです。
　\(\hspace{10pt}\mathrm{△AHE}=\color{red}{9}\)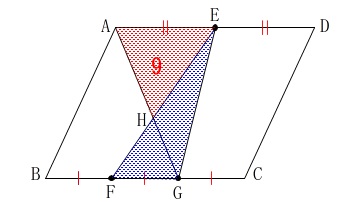このとき\(\,\mathrm{△EFG}\,\)の面積です。
線分\(\,\mathrm{AD}\,\)は二等分、線分\(\,\mathrm{BC}\,\)は三等分されているので、
全体を最小公倍数の\(\,\color{red}{⑥}\,\)とします。
（基準になる面積があるので相似比を見つけるためです。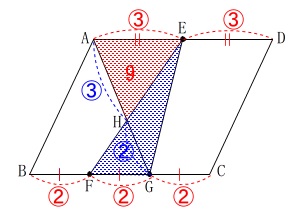）この後はいろいろな方法があります。
\(\,\mathrm{△AHE}\,\)に比べて\(\,\mathrm{△EFG}\,\)は、
底辺が\(\,\displaystyle \color{red}{\frac{2}{3}}\,\)倍、高さが\(\,\displaystyle \color{blue}{\frac{5}{3}}\,\)倍になるので、
求める体液を\(\,V\,\)とすると
　\(\begin{eqnarray}
V&=&\color{red}{9}\times \color{red}{\frac{2}{3}}\times \color{blue}{\frac{5}{3}}\\
&=&\underline{　10　}
\end{eqnarray}\)
部分的な面積もでます。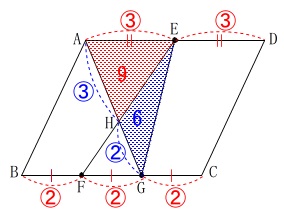高さが共通とみて、
底辺が\(\,\mathrm{AH:HG=3:2}\,\)なので
　\(\begin{eqnarray}
\mathrm{△EHG}&=&\frac{2}{3}\times \mathrm{△AHE}\\
&=&\frac{2}{3}\times 9\\
&=&\color{blue}{6}
\end{eqnarray}\)
また\(\,\mathrm{HE:HF=3:2}\,\)なので
　\(\begin{eqnarray}
\mathrm{△HFG}&=&\frac{2}{3}\times \mathrm{△EHG}\\
&=&\frac{2}{3}\times 6\\
&=&\color{blue}{4}
\end{eqnarray}\)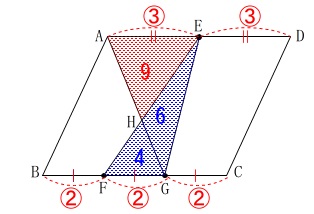合わせれば求める面積です。
\(\,\mathrm{△AHE}\,\)∽\(\,\mathrm{△GHF}\,\)で相似比が\(\,3:2\,\)なので
面積比が\(\,9:4\,\)としても良いです。

平行四辺形全体や全ての部分の面積が分かるので何でも良いです。

第４問

\(\color{black}{\fbox{4}}\)
一次関数と図形の性質です。
関数：\(\displaystyle \,y=\frac{2}{3}\,x+2\,\)
点\(\,\mathrm{A}\,\)は定点で\(\,(\,0\,,\,8\,)\,\)です。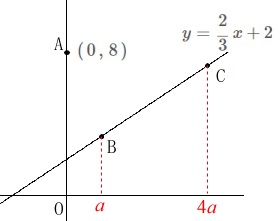点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を仮に\(\,\color{red}{a}\,\)としています。
(1)
線分\(\,\mathrm{AC}\,\)が\(\,x\,\)軸に平行になるのは、
\(\,\mathrm{A\,,\,C}\,\)の\(\,y\,\)座標が等しくなるときので
　\(\begin{eqnarray}
8&=&\frac{2}{3}\,x+2\\
x&=&9
\end{eqnarray}\)
点\(\,\mathrm{C}\,\)の座標は\(\,(\,9\,,\,8\,)\,\)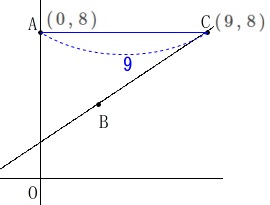線分\(\,\mathrm{AC}\,\)の長さは\(\,x\,\)座標の差なので
　\(\hspace{10pt}\mathrm{AC}=\underline{　9　}\)

(2)
条件を満たすときの直線の傾きを求めます。
条件：\(\,\mathrm{DB=BC}\,\)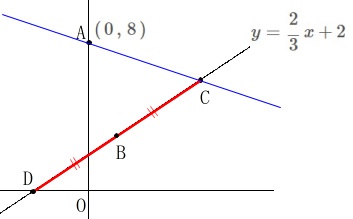点\(\,\mathrm{D}\,\)は直線\(\,\mathrm{BC}\,\)と\(\,x\,\)軸（\(\,y=0\,\)）との交点なので
　\(\begin{eqnarray}
0&=&\frac{2}{3}\,x+2\\
x&=&-3
\end{eqnarray}\)
これから\(\,\mathrm{D}\,\)の座標は\(\,(\,-3\,,\,0\,)\,\)です。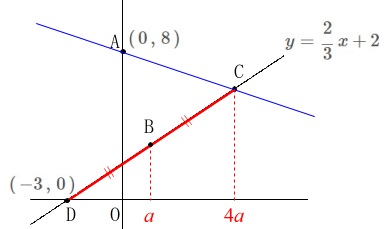条件を満たすのは、\(\,x\,\)座標の差だけで見れば良いので、
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を\(\,a\,\)、点\(\,\mathrm{C}\,\)の\(\,x\,\)座標を\(\,4a\,\)とすると
　\(\begin{eqnarray}
\mathrm{DB}&=&\mathrm{BC}\\
a-(-3)&=&4a-a\\
a+3&=&3a\\
a&=&\frac{3}{2}
\end{eqnarray}\)
このとき点\(\,\mathrm{C}\,\)の\(\,x\,\)座標は
　\(\hspace{10pt}\displaystyle x=\,\color{red}{4a}\,=4\times \frac{3}{2}=6\)
点\(\,\mathrm{C}\,\)の座標は直線\(\,\mathrm{BC}\,\)の関数に代入して
　\(\hspace{10pt}\mathrm{C}\,(\,6\,,\,6\,)\)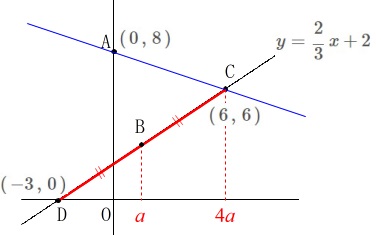よって求める直線\(\,\mathrm{AC}\,\)の「傾き」は、
（２点\(\,\mathrm{A\,,\,C}\,\)の座標から）
　\(\hspace{10pt}\displaystyle \frac{6-8}{6-0}=\underline{\underline{　-\frac{1}{3}　}}\)

直線\(\,\mathrm{AC}\,\)の\(\,y\,\)切片は点\(\,\mathrm{A}\,\)で分かっているので直線の式は
　\(\hspace{10pt}\displaystyle y=-\frac{1}{3}\,x+8\)
ですが求める必要はありません。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式を求める方法は、必ず見直しておいた方が良いです。

第５問

\(\color{black}{\fbox{5}}\)
確率と連立方程式です。

文章が長いので嫌になるかもしれませんが、
条件さえ合わせるようにすれば難しくありません。
(1)
これは確率で別問題です。

問題は５人から２人を選ぶとき、特定のひとりが選ばれる確率です。
問題を置き換えて考えると分かり易いですよ。
「１から５までの数字から２つ選びます。
そのとき１が含まれる確率は？」
と同じです。（\(\,\color{red}{1}\,\)を\(\,\mathrm{P}\,\)さんだと思えば良い。）

数字（人）は１つしかないので、
組合わせでも樹形図でも良いです。
組み合わせでやってみましょう。
　\((\,\color{red}{1}\,,\,2\,)\,,\,(\,\color{red}{1}\,,\,3\,)\,,\,(\,\color{red}{1}\,,\,4\,)\,,\,(\,\color{red}{1}\,,\,5\,)\\
(\,2\,,\,3\,)\,,\,(\,2\,,\,4\,)\,,\,(\,2\,,\,5\,)\\
(\,3\,,\,4\,)\,,\,(\,3\,,\,5\,)\\
(\,4\,,\,5\,)\)

答え　\(\hspace{10pt}\displaystyle \frac{4}{10}=\underline{\underline{　\frac{2}{5}　}}\)

樹形図でも同じなのでやってみて下さい。
(2)
これが長い文章が関係する連立方程式の問題です。
【作成方針】にあわせて表２を作成しますが、
変えないところなどが書かれているのでややこしいです。
（ここを読み取ることが問題です。）
ただ、求めるものが問題にあるので条件に合わせて連立させると楽です。

在校生インタビューの配分時間を\(\,x\,\)秒、
部活動紹介の配分時間を\(\,y\,\)秒とすると、
１５分の残り時間は５分（\(\,300\,\)秒）だから
　\(\hspace{10pt}x\,+\,y\,=\,300　･･･①\)

【作成方針】（\(\,\mathrm{Ⅲ}\,\)）から
在校生ひとりのインタビュー時間は
　\(\hspace{10pt}\displaystyle \frac{x}{3}\)
【作成方針】（\(\,\mathrm{Ⅳ}\,\)）から
代表の部活動３つに割り当てられる時間は\(\,y-30\,\)（秒）で、
均等に割り当てられるので部活動１つに割り当てる時間は
　\(\hspace{10pt}\displaystyle \frac{y-30}{3}\)
これは在校生ひとりのインタビュー時間の\(\,1.5\,\)倍だから
　\(\hspace{10pt}\displaystyle \frac{y-30}{3}=\frac{x}{3}\times \frac{3}{2}　･･･②\)

\(\,①②\,\)を連立して
　\(\hspace{10pt}x=108\,,\,y=192\)（単位は「秒」です。）

答え
\(\hspace{10pt}\color{black}{\fbox{　ア　}}　\underline{　1　}分\underline{　48　}秒\)
\(\hspace{10pt}\color{black}{\fbox{　イ　}}　\underline{　3　}分\underline{　12　}秒\)

\(\,②\,\)は両辺を６倍して
　\(\hspace{10pt}2(y-30)=3\,x　･･･②’\)
とすれば普通に加減法で計算できると思うので省略します。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

代入法も同じで、連立方程式を解くには一文字消去です。

第６問

\(\color{black}{\fbox{6}}\)
正方形が２つの図形問題です。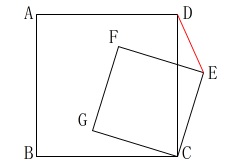【問題】は線分\(\,\mathrm{DE}\,\)と長さが同じもの、です。
【予想】は\(\,\mathrm{DE=BG}\,\)で、それを証明します。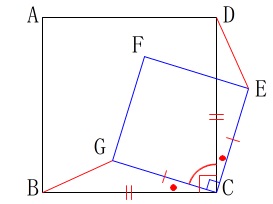正方形\(\,\mathrm{CEFG}\,\)は点\(\,\mathrm{C}\,\)を中心に回転させたと考えると、
　\(\hspace{10pt}\mathrm{∠BCG=∠DCE}\)
なので合同の証明は簡単です。
（図の中で証明は終わっているのでまとめます。）

【証明】
\(\hspace{4pt}\,\mathrm{△CED}\,\)と\(\,\mathrm{△CGB}\,\)において　
\(\hspace{10pt}\mathrm{DC=BG}　(\,正方形の１辺\,)　･･･①\)
\(\hspace{10pt}\mathrm{CE=CG}　(\,正方形の１辺\,)　･･･②\)
また正方形の１角は\(\,90°\,\)なので、
\(\hspace{10pt}\mathrm{\color{red}{∠DCE}}=90°-\mathrm{\color{blue}{∠DCG}}\)
\(\hspace{10pt}\mathrm{\color{red}{∠BCG}}=90°-\mathrm{\color{blue}{∠DCG}}\)
このことから（\(\,90°\,\)から共通の角を引いている）
\(\hspace{10pt}\mathrm{\color{red}{∠DCE}}=\mathrm{\color{red}{∠BCG}}　･･･③\)
①②③から２組の辺とその間の角がそれぞれ等しいので
\(\hspace{10pt}\mathrm{△CED}\,\)≡\(\,\mathrm{△CGB}\,\)
合同な図形の対応する辺は等しいから
\(\hspace{10pt}\mathrm{DE=BG}\)

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

【証明】の始まりは決められているので、
ルール通りに記号の順番には気をつけましょう。
合同条件をそろえる順番や根拠の書き方は好きにしていいです。

(2)
条件はそのままに、さらに言えることを探します。
（記号や線分は補助されます。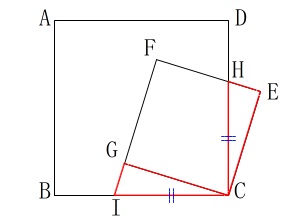）(1)の証明と同様に
　\(\,\mathrm{△CEH}\,\)≡\(\,\mathrm{△CGI}\,\)
なので
　\(\hspace{10pt}\mathrm{CH=CI}\)
このほかに言えることを探しますが、
全てを選ぶので全てを見ていきましょう。

ア「四角形\(\,\mathrm{AICH}\,\)はひし形である。」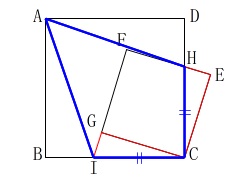明らかに違います。×
（ひし形は４辺が等しい。）
イ「四角形\(\,\mathrm{AICH}\,\)の面積は、三角形\(\,\mathrm{CDI}\,\)の２倍である。」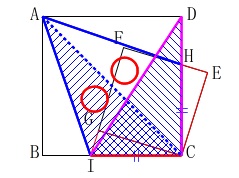\(\,\mathrm{△CDI}\,\)と\(\,\mathrm{△CAI}\,\)は底辺と高さが等しいので面積は同じ、
また、\(\,\mathrm{△CAI}\,\)と\(\,\mathrm{△AHC}\,\)は対称で合同だから面積は同じなので、
四角形\(\,\mathrm{AICH}\,\)の面積は\(\,\mathrm{△CDI}\,\)の２倍です。○
ウ「線分\(\,\mathrm{BD}\,\)と線分\(\,\mathrm{IH}\,\)は平行である。」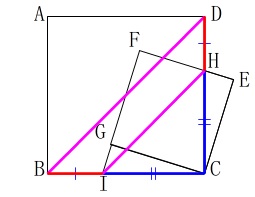簡単に言えば、
\(\,\mathrm{△CBD}\,\)と\(\,\mathrm{△CIH}\,\)は直角二等辺三角形なので、
\(\hspace{10pt}\mathrm{BD}\,\)∥\(\,\mathrm{IH}\,\)は言えます。○
エ「\(\,\mathrm{△BIH}\,\)≡\(\,\mathrm{△DHG}\,\)である。」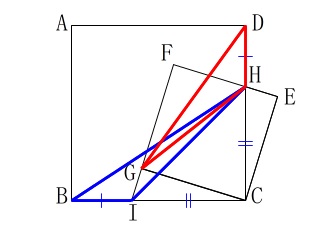合同条件がそろいません。
\(\hspace{10pt}BH=DI\)は言えますが、
\(\,\mathrm{BH}\,\)と\(\,\mathrm{DG}\,\)は等しくありません。×
オ「４点\(\,\mathrm{C\,,\,H\,,\,F\,,\,I}\,\)は１つの円周上にある。」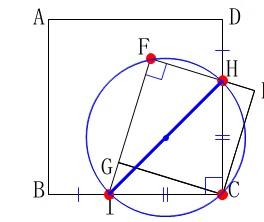円周角が\(\,90°\,\)であることから、
線分\(\,\mathrm{IH}\,\)を直径とする円周上にあることが分かります。○