2023年（令和5年）度長野県公立高校入試の数学の問題と解説

2023年（令和5年）度長野県公立高校入試の数学の問題と解説です。
大問４問で基本から標準の問題構成でしつこい計算もないので、
ある程度の作業は必要ですが基本を抑えておけば時間的にもきつくはないでしょう。
ただし、手を止めてたら答えまでたどり着かないのはどこも同じです。

2023年（令和5年）度長野県公立高校入試の数学の問題

令和５年度の長野県公立高校入試数学の問題です。

⇒　2023年（令和5年）度長野県公立高校入試の数学の問題PDF

問題は問１から問４までの４問です。
問題の表紙にある注意書きにややこしいことは書いていませんが、
例年それ程変わらないので受験生は先に目を通しておいた方が良いですね。

2023年（令和5年）度長野県公立高校入試の数学の解説

問題数は少なくはありませんが１問１問は重くないので、
時間に余裕を持たせられるよう手際よく処理していきましょう。

ここでの解説の解法は１つの例でしかありません。
数学の解法は１つではありませんので、
自分の解法にも自信を持っていて良いですよ。

問１小問集合

\(\,問１\,\)
(1)正の数負の数の計算です。
　\(\hspace{10pt}-3+4\\
=\underline{　1　}\)

足し算引き算は数直線上での移動で確認しましょう。
(2)
計算結果の符号がいつも正になる式を選びます。
　\(\hspace{4pt}5+n\,\)：×（反例：\(\,n=\,-2\)
　\(\hspace{4pt}5-n\,\)：○
　\(\hspace{4pt}\displaystyle 5\times n\)：×（常に負です。）
　\(\hspace{4pt}\displaystyle 5\div n=\,5\times \frac{1}{n}\,\)：×（掛け算と同じで常に負です。）

「いつでも」なので反例が１つでもあればダメです。
(3)
　\(\hspace{10pt}\displaystyle \frac{3x-5y}{2}-\frac{2x-y}{4}\\
\displaystyle =\frac{2(3x-5y)-(2x-y)}{4}\\
\displaystyle =\frac{6x-10y-2x+y}{4}\\
\displaystyle =\underline{\underline{　\frac{4x-9y}{4}　}}\)

分数計算はいつも通り分子の計算に集中できる形にしましょう。
３行目は省略しない方が計算ミスが減ります。
答えは\(\,\displaystyle x-\frac{9}{4}\,y\,\)としても良いですが、
必要ありません。

(4)
因数分解します。
　\(\hspace{4pt}(x-3)^2+2(x-3)-15\)

まとまりが明らかなので一度文字でおいて、元に戻すと早いです。
\(\hspace{4pt}\color{red}{x-3}=t\)とします。（文字は何でも良いです。）
　\(\hspace{10pt}(\color{red}{x-3})^2+2(\color{red}{x-3})-15\\
=t^2+2t-15\\
=(t+5)(t-3)\\
=(\color{red}{x-3}+5)(\color{red}{x-3}-3)\\
=\underline{　(x+2)(x-6)　}\)

展開して因数分解しても大した差はありません。
　\(\hspace{10pt}(x-3)^2+2(x-3)-15\\
=x^2-6x+9+2x-6-15\\
=x^2-4x-12\\
=\underline{　(x+2)(x-6)　}\)

いずれにしても二次式の因数分解は定数項に着目ですね。

⇒　因数分解とは？公式がいらなくなる問題の解き方のポイント(中学3年)

因数分解は公式として覚えておいたものが多いですが、
ある程度は作業しないと定数は定まりません。

(5)
２次方程式を解きます。
　\(\hspace{4pt}x^2+2x-1=0\)
左辺が因数分解できないので解の公式です。
　\(\begin{eqnarray}
x&=&\frac{-(2)\pm \sqrt{(2)^2-4\cdot (1)\cdot (-1)}}{2\times 1}\\
&=&\frac{-2\pm \sqrt{8}}{2}\\
&=&\frac{-2\pm 2\sqrt{2}}{2}\\
&=&\underline{　-1\pm \sqrt{2}　}
\end{eqnarray}\)
※
ルートの中の「\(\,\cdot\,\)」は掛け算の意味です。

１次の係数が偶数なので
　\(\begin{eqnarray}
x&=&\frac{-1\pm \sqrt{1^2-1\cdot (-1)}}{1}\\
&=&-1\pm \sqrt{2}
\end{eqnarray}\)
とした人もいるでしょう。
もちろん構いません。

(6)
問題文の条件から\(\,x\,,\,y\,\)の関係式は
　\(\hspace{4pt}xy=12\hspace{10pt}または\hspace{10pt}\displaystyle y=\frac{12}{x}\)
つまり、反比例の関係を表すものを選べば良いのです。

選ぶのは２つと書いてくれているので間違えは減りますね。
答え　\(\,\underline{　イ\,,\,ウ　}\,\)
(7)
近似値問題です。
（久しぶり？）

小数第１位を四捨五入して\(\,31\,\)になるのは
　\(\hspace{10pt}\underline{　30.5\,≦\,a\,＜\,31.5　}\)

⇒　近似値とは？誤差の大きさと真の値の範囲の表し方(中１資料の活用)

みんなが忘れた頃にタイミング良く出題してくれました。
高校生でも有効数字や近似値は忘れがちです。

(8)
取り出した玉の色が異なる確率です。
２個取り出しますが元に戻さないので、同時に２個取り出すのと同じです。
同じ色があるので区別すると樹形図で終わります。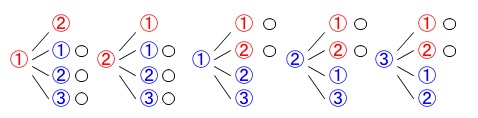左が１回目、右が２回目と見て良いです。
（いつもは自分で書いてもらうけど、久しぶりに樹形図書いたな。）
　\(\hspace{10pt}\displaystyle \frac{12}{20}=\underline{\underline{　\frac{3}{5}　}}\)

異なる色を取り出すのは取り出す順に
　\(\hspace{4pt}\color{red}{赤}－\color{blue}{青}　または　\color{blue}{青}－\color{red}{赤}\)
なので１個目は５個の中から、
２個目は４個の中から取り出すので
　\(\hspace{4pt}\displaystyle \frac{\color{red}{2}}{5}\times \frac{\color{blue}{3}}{4}+\frac{\color{blue}{3}}{5}\times \frac{\color{red}{2}}{4}=\frac{12}{20}=\frac{3}{5}\)
でも良いです。

(9)
連立方程式の意味です。

連立方程式の解はどちらの方程式も満たすので、
見えている方程式に解\(\,x=2\,\)を代入すると\(\,y\,\)が求まります。
　\(\begin{eqnarray}
(2)+y&=&-1\\
y&=&-3
\end{eqnarray}\)
連立方程式の解は
　\(\hspace{4pt}x=2\,,\,y=-3\,\)
これを満たす方程式は
　\(\hspace{10pt}\underline{　x-3y\,=\,11　}\)

時間はかかりますが４つの方程式を連立しても良いです。

(10)
垂線の作図です。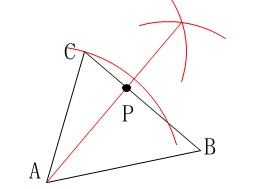垂線なので説明は不要でしょう。
（ひし形利用でも良いですよ。）

点\(\,\mathrm{P}\,\)が\(\,\mathrm{BC}\,\)上の点だと示すことを忘れないように。

(11)
求めるのは外角なので迷うこともないでしょう。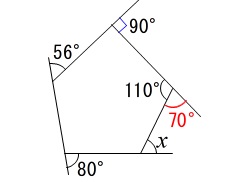多角形の外角の和は角数に関係なく一定で\(\,360°\,\)なので
　\(\begin{eqnarray}
70°+90°+56°+80°+∠x&=&360°\\
∠x&=&\underline{　64°　}
\end{eqnarray}\)

(12)
球と円柱の体積を求める事ができるどうかです。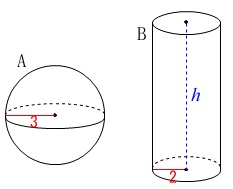円柱\(\,\mathrm{B}\,\)の高さを\(\,\color{blue}{h}\,\)として方程式にします。

球\(\,\mathrm{A}\,\)と円柱\(\,\mathrm{B}\,\)の体積が等しいので
　\(\begin{eqnarray}
\frac{4}{3}\,\pi\,(3)^3&=&\pi\,(2)^2\times \color{blue}{h}\\
36\,\pi&=&4\,\pi\,h\\
h&=&\underline{　9　}(\,\mathrm{cm}\,)
\end{eqnarray}\)

中学までは球の体積や表面積は公式を覚えていないと求める事はできません。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

試験会場で求め方を考えても仕方ないので覚えましょう。

問２データと文字式

\(\,問２\,\)
\(\,\mathrm{Ⅰ}\,\)
箱ひげ図とヒストグラムの読み取りです。
(1)
ヒストグラムと箱ひげ図を一致させますが、
箱ひげ図もヒストグラムも元の完全なデータは分かりません。

ただ、だいたいの分布は分かります。
例えば、
箱ひげ図では最大値や最小値および四分位数が読み取れます。
ヒストグラムからは代表値や階級や度数などが読み取れます。
図２から読み取れるのは、
最小値がある階級が２８以上３０未満であること、
最大値がある階級が３８以上４０未満であること。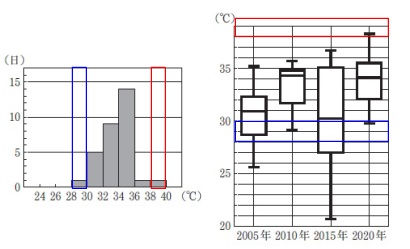中央値などを見比べても一致していますが、
最大値最小値だけでも一致するのは１つしかありません。

答え　\(\,\underline{　2020\,年　}\,\)

(2)
箱ひげ図の読み取りです。
①
「散らばり」が２番目に小さいのは２０２０年か？
データの散らばりを簡単に見る方法の１つに「範囲」があります。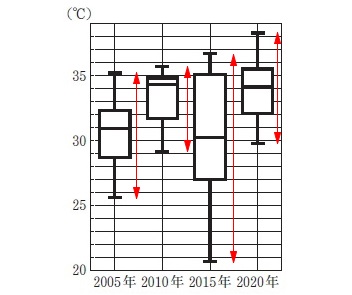範囲は最大値と最小値の差なので、
２０２０年の散らばりは２番目に小さいです。
「正しい。」
②
２００５年は３５°超えた日は１日しかないか？
最大値が３５°を超えているので確実にありますが、
１日でも、２日あったとしても箱ひげ図は同じになります。
「少なくとも１日は３５°を超えている。」が正しい表現です。
「分からない」
(3)
四分位数についてです。
\(\,2010\,\)年と\(\,2015\,\)年の箱ひげ図から分かることをまとめてあります。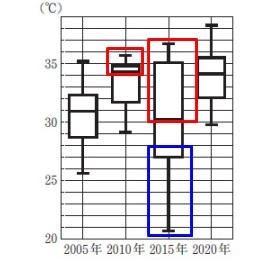・\(\,2015\,\)年で\(\,\mathrm{30\,℃}\,\)を超えている。
・\(\,2010\,\)年で\(\,\mathrm{34\,℃}\,\)を超えている。
これらで共通しているのは第２四分位数（中央値）を含んでいることです。
答え　\(\color{black}{\fbox{　あ　}}\)　\(\,\underline{　50\,％　}\,\)

・\(\,2015\,\)年で\(\,\mathrm{27\,℃}\,\)以下である。
含んでいるのは第１四分位数です。
答え　\(\color{black}{\fbox{　い　}}\)　\(\,\underline{　25\,％　}\,\)

四分位数は度数で区切られていることは忘れないようにしましょう。
　\(○○○\color{blue}{●}○○○\color{red}{●}○○○\color{magenta}{●}○○○\)

\(\,\mathrm{Ⅱ}\,\)
規則性と思わせて単なる文字式の処理なので簡単に済ませます。

〔ノート〕に書いてる順にうめていけば良いですよ。
(1)
　\(\hspace{10pt}a=mn\,,\,b=m(n+1)\,,\,c=m(n+2)\)
から
　\(\hspace{10pt}a+b+c\\
=mn+m(n+1)+m(n+2)\\
=mn+mn+m+mn+2m\\
=3mn+3m\\
=3m(n+1)\)
ここで\(\,b=m(n+1)\,\)なので
　\(\hspace{10pt}a+b+c=3b\)

３行目以降は
　\(\hspace{10pt}m(n+n+1+n+2)\\
=m(3n+3)\\
=3m(n+1)\)
でも良いです。（３行目自体省略しても良いです。）
(2)
連続して並ぶ５つの数についても、
同じような関が成り立つらしいので(1)と同じことをすれば良いです。

最初に選んだ数\(\,a\,\)を、\(\,m\,\)行、\(\,n\,\)列目の数とすると
　\(\hspace{4pt}a=mn\)
　\(\hspace{4pt}b=m(n+1)\)
　\(\hspace{4pt}c=\color{red}{m(n+2)}\)
　\(\hspace{4pt}d=m(n+3)\)
　\(\hspace{4pt}e=m(n+4)\)
これら５つの数の和は
　\(\hspace{10pt}a+b+c+d+e\\
=mn+m(n+1)+m(n+2)+m(n+3)+m(n+4)\\
=m(n+n+1n+2+n+3+n+4)\\
=m(5n+10)\\
=5\color{red}{m(n+2)}\)
ここで\(\,m(n+2)=c\,\)なので
　\(\hspace{10pt}a+b+c+d+e\\
=5\,c\)
このことから５つの数の和を５で割ると\(\,c\,\)となることが分かります。
答え　\(\color{black}{\fbox{　う　}}\)　\(\,\underline{　5　}\,\)　\(\color{black}{\fbox{　え　}}\)　\(\,\underline{　c　}\,\)

さらに１１行目にある５つの数の和が６０５であるとき、
\(\,m\,=\,\color{blue}{11}\,\)なので
　\(\begin{eqnarray}
5\times \color{blue}{11}\times (n+2)&=&605\\
n+2&=&11\\
n&=&\color{red}{9}
\end{eqnarray}\)
このとき
　\(\begin{eqnarray}
a&=&mn\\
&=&\color{blue}{11}\times \color{red}{9}\\
&=&\underline{　99　}
\end{eqnarray}\)

日本語の文字が多い問題ですが、
文字が使えると数学では日本語少なくて良いですよね。

問３関数

\(\,問３\,\)
\(\,\mathrm{Ⅰ}\,\)
１次関数の文章題になっていますが基本を聞いているだけなので、
余り深く考えなくて良いです。

表と図があります。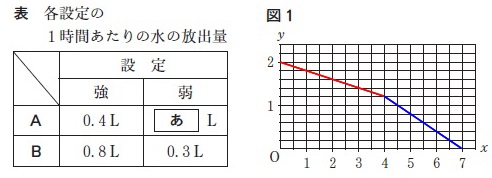(1)
先ずは\(\,\mathrm{A}\,\)を使ったときの水の放出量です。
\(\,①\,\)
表の\(\color{black}{\fbox{　あ　}}\)に入る数字は、
図１の赤線部分の直線の傾きです。
\(\,4\,\)時間で\(\,\mathrm{0.8\,L}\,\)減っているので
　\(\hspace{10pt}\displaystyle \color{black}{\fbox{　あ　}}=\frac{0.8}{4}=\underline{　0.2　}\)
\(\,②\,\)
\(\,x\,\)の変域が\(\,4≦x≦7\,\)の\(\,x\,,\,y\,\)の関係式を求めます。
青色部分の直線の式です。
　\(\hspace{4pt}(\,4\,,\,1.2\,)\)
　\(\hspace{4pt}(\,7\,,\,0\,)\)
を通る直線なので１次関数で傾きは
　\(\hspace{10pt}\displaystyle \frac{0-1.2}{7-4}=-0.4\)
求める関係式は
　\(\hspace{10pt}y=-0.4\,x+b\)
とおけて\(\,(\,7\,,\,0\,)\,\)を通るので
　\(\hspace{10pt}\underline{　y=-0.4\,x+2.8　}\)

関係式になっていれば良いので係数は分数でも整数でも良いですよ。
　\(\hspace{10pt}\displaystyle y=-\frac{2}{5}\,x+\frac{14}{5}\)
　\(\hspace{10pt}5y=-2\,x+14\)
（解答用紙によってこの設定はなかった。\(\,y=\underline{　　}\,\)だけ。）
(2)
今度は\(\,\mathrm{B}\,\)を使いますが、
「強」「弱」での水の減り方（傾き）は分かっています。

(1)とは違っていて「強」から「弱」に切り替わります。
「強」のとき傾き\(\,-0.8\,\)で\(\,(\,0\,,\,3\,)\,\)を通る直線で
　\(\hspace{10pt}\displaystyle y=-0.8\,x+3\)
「弱」のとき傾き\(\,-0.3\,\)で\(\,(\,8\,,\,0\,)\,\)を通る直線で
（\(\,8\,\)時間後タンクの水がなくなるので）
　\(\hspace{10pt}y=-0.3\,x+2.4\)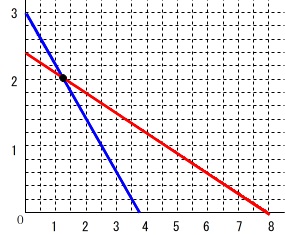「強」から「弱」に切り替わったのは、
この２本の直線の\(\color{black}{\fbox{　交点　}}\)の\(\color{black}{\fbox{　\(\,x\,\)　}}\)座標です。

交点は連立すれば求まるので
　\(\begin{eqnarray}
-0.8x+3&=&-0.3x+2.4\\
-8x+30&=&-3x+24\\
6&=&5\\
x&=&\frac{6}{5}\\
&=&1+\frac{1}{5}　(\,時間\,)
\end{eqnarray}\)
この\(\,x\,\)座標が切り替わった時間なので
　\(\hspace{10pt}\underline{　1　}(\,時間\,)\underline{　12　}(\,分後\,)\)
※
\(\displaystyle \frac{1}{5}\,(\,時間\,)\)は\(\displaystyle \,\frac{1}{5}\times 60\,=\,12\,(\,分\,)\)。

\(\,\mathrm{Ⅱ}\,\)
今度は２次関数です。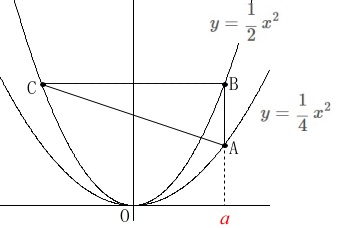関数は
　\(\hspace{10pt}\displaystyle y=\frac{1}{4}\,x^2\)
　\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x^2\)
点\(\,\mathrm{A\,,\,B}\,\)は\(\,x\,\)座標が正の数\(\,a\,\)で同じで、
点\(\,\mathrm{C}\,\)は点\(\,\mathrm{B}\,\)と\(\,y\,\)軸について対称、つまり\(\,y\,\)座標が同じです。
(1)
\(\,a=4\,\)のときですがこの問題だけの条件です。
\(\,x\,\)座標が\(\,4\,\)のとき
　\(\mathrm{A}\,(\,4\,,\,\color{red}{4}\,)\,,\,\mathrm{B}\,(\,4\,,\,\color{blue}{8}\,)\)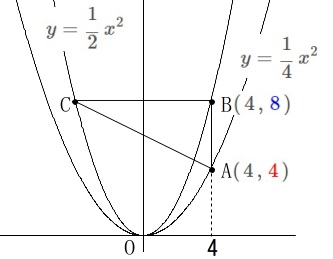\(\,\mathrm{AB}\,\)の長さは\(\,y\,\)座標ので求まります。
　\(\hspace{10pt}\mathrm{AB}=\,\color{blue}{8}-\color{red}{4}\,=\,\underline{　4　}\)
(2)
\(\,x=a\,\)のとき\(\,\mathrm{A\,,\,B\,,\,C}\,\)の座標を\(\,a\,\)用いて表すと、
　\(\displaystyle \mathrm{A}\,\left(\,a\,,\,\frac{1}{4}\,a^2\,\right),\,\mathrm{B}\,\left(\,a\,,\,\frac{1}{2}\,a^2\,\right)\,\mathrm{C}\,\left(\,-a\,,\,\frac{1}{2}\,a^2\,\right)\)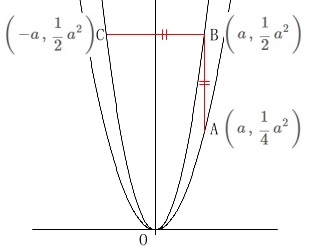\(\,\mathrm{AB}\,\)と\(\,\mathrm{BC}\,\)が等しくなるとき、
\(\,y\,\)座標の差と\(\,x\,\)座標の差が等しくなるときで
　\(\begin{eqnarray}
\frac{1}{2}\,a^2-\frac{1}{4}\,a^2&=&a-(-a)\\
\frac{1}{4}\,a^2&=&2a\\
a^2&=&8\,a\\
a(a-8)&=&0\\
a&=&0\,,\,8
\end{eqnarray}\)
\(\,\mathrm{A}\,\)の\(\,x\,\)座標\(\,a\,\)は正の数なので
　\(\hspace{10pt}a=\underline{　8　}\)

(3)
今度は\(\,a\,\)が決まっています。
　\(\hspace{10pt}a=2\)
このとき点\(\,\mathrm{A\,,\,B\,,\,C}\,\)は定まります。
　\(\hspace{4pt}\mathrm{A}\,(\,2\,,\,1\,)\,,\,\mathrm{B}\,(\,2\,,\,2\,)\,,\,\mathrm{C}\,(\,-2\,,\,2\,)\)
点\(\,\mathrm{P}\,\)は\(\,y\,\)軸上の点で\(\,2\,\)より大きい点です。
①
\(\,\mathrm{△BCP}\,\)と\(\,\mathrm{△ABC}\,\)の面積が等しくなるときの点\(\,\mathrm{P}\,\)の座標を求めます。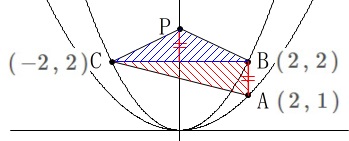底辺\(\,\mathrm{BC}\,\)を共通とするので、
高さ（\(\,y\,\)座標の差）が等しければ同じ面積になります。
点\(\,\mathrm{P}\,\)の座標を\(\,(\,0\,,\,b\,)\,\)としておきましょう。
　\(\begin{eqnarray}
b-2&=&2-1\\
b&=&3
\end{eqnarray}\)
よって求める点\(\,\mathrm{P}\,\)の座標は
　\(\hspace{4pt}\mathrm{P}\,\underline{　(\,0\,,\,3\,)　}\)

\(\,\mathrm{△ABC}\,\)の面積は具体的に求まるので、
\(\,\mathrm{△BCP}\,\)の面積も\(\,b\,\)で表せるので求まりますが、
高さだけで比べれば良いですね。

②
今度は\(\,\mathrm{△ACP}\,\)と\(\,\mathrm{△ABC}\,\)の面積が等しくなるときです。
点\(\,\mathrm{P}\,\)の座標は\(\,(\,0\,,\,b\,)\,\)のままにしておきます。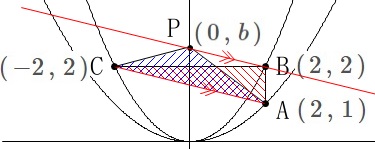①でも言っていますが、
\(\,\mathrm{△ABC}\,\)の面積は具体的なので、
\(\,\mathrm{△ACP}\,\)の面積を\(\,b\,\)を使って表しても求まりますが、
ここは平行線の等積移動で求めましょう。

直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{BP}\,\)の傾きが同じになるとき面積は等しくなるので、
　\(\begin{eqnarray}
\frac{1-2}{2-(-2)}&=&\frac{2-b}{2-0}\\
-\frac{1}{4}&=&\frac{2-b}{2}\\
-1&=&2(2-b)\\
2b&=&5\\
b&=&\frac{5}{2}
\end{eqnarray}\)
求める点\(\,\mathrm{P}\,\)の座標は
　\(\hspace{10pt}\displaystyle \mathrm{P}\,\underline{　\left(\,0\,,\,\frac{5}{2}\,\right)　}\,\)

傾きだけじゃなくて直線\(\,\mathrm{AC}\,\)を求めた人もいるでしょう。
　\(\hspace{10pt}\displaystyle y=-\frac{1}{4}\,x+\frac{3}{2}\)
（利用するのは傾きだけですが、）
直線\(\,\mathrm{PB}\,\)の式は直線\(\,\mathrm{AC}\,\)と平行で\(\,(\,2\,,\,2\,)\,\)通るので、
　\(\hspace{10pt}\displaystyle y=-\frac{1}{4}\,x+\frac{5}{2}\)
点\(\,\mathrm{P}\,\)はこの直線の\(\,y\,\)切片だから
　\(\hspace{10pt}\displaystyle \mathrm{P}\,\underline{　\left(\,0\,,\,\frac{5}{2}\,\right)　}\,\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

いずれにしても傾き（変化の割合）は求められる、
というかたった４つの関数は求められるようになっておきましょう。

問４平面図形

\(\,問４\,\)
平面図形、円と三角形？です。
〔作図の手順」で書かれていることが条件です。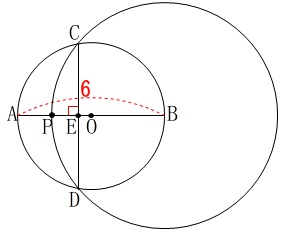手順の下にある「なお、点\(\,\mathrm{P}\,\)を線分\(\,\mathrm{AB}\,\)上の、、、」
で書かれている\(\,\mathrm{AB}\,\)⊥\(\,\mathrm{DC}\,\)があるのでちゃちゃっと終わらせましょう。
(1)
線分\(\,\mathrm{AP=2}\,\)のときです。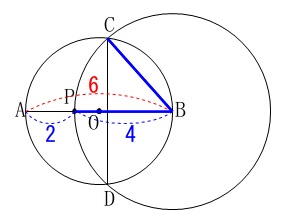※長さは\(\,\mathrm{cm}\,\)です。

\(\,\mathrm{PB=4}\,\)となり、半径は等しいので
　\(\hspace{10pt}\mathrm{PB=BC}=\underline{　4　}(\,\mathrm{cm}\,)\)

(2)
点\(\,\mathrm{P}\,\)と\(\,\mathrm{O}\,\)が重なる（半径が等しい）ときです。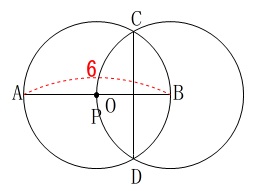半径は常に等しいので正三角形が見えてきます。
①
\(\,\mathrm{∠ACP}\,\)を求めます。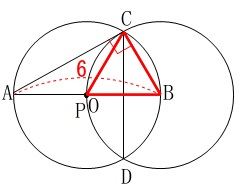\(\,\mathrm{△PCB}\,\)は正三角形で、
\(\,\mathrm{∠ACB}\,\)は直径（半円）に対する円周角なので\(\,90°\,\)だから
　\(\hspace{10pt}\mathrm{∠ACP}=90°-60°=\underline{　30°　}\)
②
線分\(\,\mathrm{ＣＤ}\,\)の長さを求めます。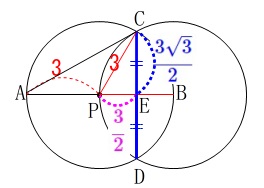正三角形があるので分かり易いですね。
　\(\hspace{10pt}\displaystyle \mathrm{PE}=\color{magenta}{\frac{3}{2}}\,,\,\mathrm{CE}=\color{blue}{\frac{3\sqrt{3}}{2}}\)
だから
　\(\hspace{10pt}\displaystyle \mathrm{ＣＤ}=2\times \mathrm{CE}=2\times \color{blue}{\frac{2\sqrt{3}}{2}}=\underline{　3\sqrt{3}　}\,(\mathrm{cm}\,)\)

(3)
証明です。
〔予想〕
①\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△CBE}\,\)は相似である。
②線分\(\,\mathrm{CP}\,\)は\(\,\mathrm{∠ACE}\,\)を二等分する。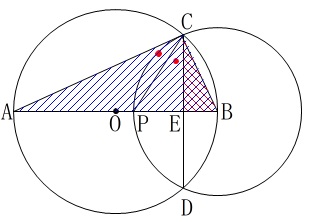それぞれを証明しますが、
穴埋めなので順にうめていけば良いです。
〔予想①の証明〕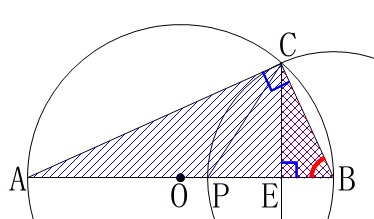図の中で証明は終わっています。
相似条件は「２組の角がそれぞれ等しい。」です。
予想②と同じセリフが入るので気をつけて、
\(\color{black}{\fbox{　あ　}}\)\(\hspace{4pt}\underline{　直径に対する円周角　}\)
残りの枠\(\color{black}{\fbox{　い　}}\)には「共通の角」を言えば相似条件がそろいます。
　\(\hspace{4pt}\mathrm{∠ABC=∠CBE}\)
相似条件は必ず入れてください。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

図形の証明の場合は記号のルールがあるので、
それさえ違えなければ書き方は好きにしていいですよ。

〔予想②の証明〕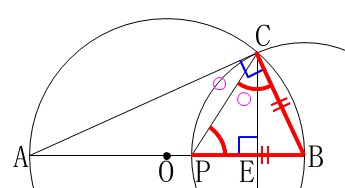半径は等しいので、
二等辺三角形の底角が等しいことをいえば良いだけです。

自分で書いていないからまとめにくいと思いますが、
証明の流れに乗って
「半径は等しい」、「\(\,\mathrm{BC＝BP}\,\)の二等辺三角形」、「底角が等しい」
などを入れてうめておけば問題ありません。

注意するのは\(\color{black}{\fbox{　え　}}\)に入れる角度です。
\(\,\mathrm{∠CPB}\)も同じ角を示していますが、
問題の証明の中で表しているのは\(\hspace{4pt}\mathrm{∠CPE}\)なので、
同じ記号を入れておく方が無難です。

(4)
面積と面積比です。
　\(\hspace{10pt}\mathrm{AP}=4\)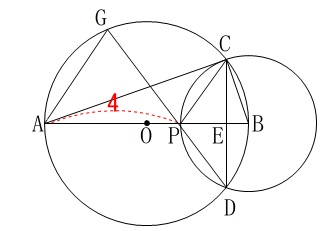①
\(\,\mathrm{△CEP}\,\)の面積を求めるので、
底辺と高さ（\(\,\mathrm{PE\,,\,CE}\,\)）を求めに行きましょう。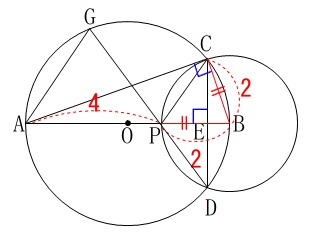(3)で証明したことを利用していきます。
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△CBE}\,\)
\(\,\mathrm{△BCP}\,\)は半径が等しい二等辺三角形だから
　\(\hspace{10pt}\mathrm{BP=BC}=\color{red}{2}\)
なので直径が\(\,\mathrm{AB=6}\,\)であることから
　\(\begin{eqnarray}
\mathrm{AB:BC}&=&\mathrm{CB:BE}\\
6:2&=&2:\mathrm{BE}\\
6\times \mathrm{BE}&=&2\times 2\\
\mathrm{BE}&=&\color{blue}{\frac{2}{3}}
\end{eqnarray}\)
このとき
　\(\begin{eqnarray}
\mathrm{PE}&=&\mathrm{PB-BE}\\
&=&2-\frac{2}{3}\\
&=&\color{magenta}{\frac{4}{3}}
\end{eqnarray}\)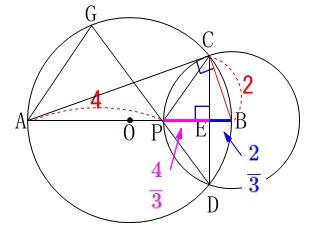相似だけでもなんとかなりそうだけど、
（\(\,\mathrm{△CAE}\,\)∽\(\,\mathrm{△BCE}\,\)）
直角三角形\(\,\mathrm{CBE}\,\)で三平方の定理を利用して、
　\(\begin{eqnarray}
\mathrm{CE^2+BE^2}&=&\mathrm{BC^2}\\
\mathrm{CE^2}+\left(\frac{2}{3}\right)^2&=&2^2\\
\mathrm{CE^2}+\frac{4}{9}&=&4\\
\mathrm{CE^2}&=&\frac{32}{9}\\
\mathrm{CE}&=&\pm \frac{4\sqrt{2}}{3}
\end{eqnarray}\)
長さなので正の数だから
　\(\hspace{10pt}\displaystyle \mathrm{CE}=\color{red}{\frac{4\sqrt{2}}{3}}\)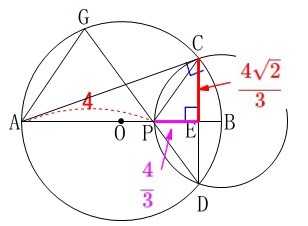求める面積は
　\(\begin{eqnarray}
\mathrm{△CEP}&=&\frac{1}{2}\times \mathrm{PE}\times \mathrm{CE}\\
&=&\frac{1}{2}\times \color{magenta}{\frac{4}{3}}\times \color{red}{\frac{4\sqrt{2}}{3}}\\
&=&\underline{\underline{　\frac{8\sqrt{2}}{9}　(\,\mathrm{cm^2}\,}}
\end{eqnarray}\)
三角形の面積は底辺と高さを求めに行くのが基本ですね。

②
\(\,\mathrm{△BCP}\,\)と\(\,\mathrm{△GAP}\,\)の面積比を求めます。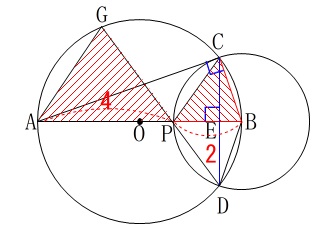\(\,\mathrm{△BCP}\,\)の面積が具体的に求まるので、（①の図参照）
\(\,\mathrm{△GAP}\,\)の面積を求めに行きたくなりますが、
\(\,\mathrm{△BCP}\,\)と\(\,\mathrm{△BDP}\,\)が合同で面積が等しいので相似でいきましょう。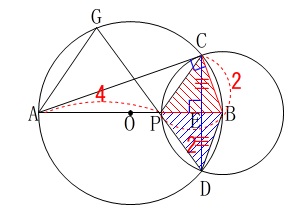求めたいのは
　\(\hspace{4pt}\mathrm{△BCP}:\mathrm{△GAP}=\mathrm{△BDP}:\mathrm{△GAP}\)
となります。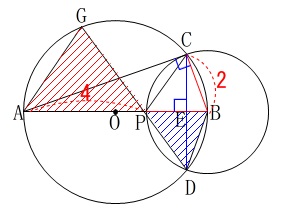２組の角等しくなるので、
　\(\,\mathrm{△BDP}\,\)∽\(\,\mathrm{△GAP}\,\)
（順番を間違えないようにしましょう。）

面積比は相似比の２乗で比べれば良いので、
相似比を求めに行きますが\(\,\mathrm{△GAP}\,\)側は\(\,\mathrm{AP=4}\,\)しか分かっていません。
\(\,\mathrm{△BDP}\,\)側の\(\,\mathrm{PD}\,\)を求めます。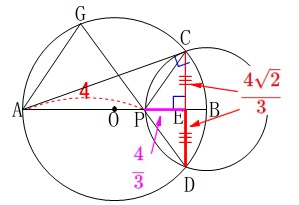①で求めている長さと\(\,\mathrm{CE=DE}\,\)から
　\(\begin{eqnarray}
\mathrm{PD^2}&=&\mathrm{PE^2+DE^2}\\
&=&\left(\frac{4}{3}\right)^2+\left(\frac{4\sqrt{2}}{3}\right)^2\\
&=&\frac{16}{9}+\frac{32}{9}\\
&=&\frac{48}{9}\\
&=&\pm \frac{4\sqrt{3}}{3}
\end{eqnarray}\)
長さなので正の数だから
　\(\hspace{4pt}\displaystyle \mathrm{PD}=\color{blue}{\frac{4\sqrt{3}}{3}}\)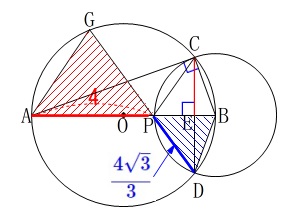相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{PD:PA}&=&\color{blue}{\frac{4\sqrt{3}}{3}}:\color{red}{4}\\
&=&\frac{\sqrt{3}}{3}:1\\
\end{eqnarray}\)
よって求める面積比は、
　\(\begin{eqnarray}
\mathrm{△BCP:△GAP}&=&\mathrm{△BDP:△GAP}\\
&=&\left(\frac{\sqrt{3}}{3}\right)^2:1^2\\
&=&\frac{1}{3}:1\\
&=&\underline{　1:3　}
\end{eqnarray}\)