2023年（令和5年度）京都府公立入試中期数学の問題と解説

2023年（令和5年度）京都府公立入試中期選抜【数学】の問題と解説です。
構成は前期と同じですが問題は少し軽めです。
といっても「前期と比べて」なので楽とは言えません。
簡単に言えば前期の受験後何ができなかったか復習しましたか？
という問題が並んでいる、という感じです。

2023年（令和5年度）京都府公立入試中期数学の問題

令和５年度中期選抜学力検査の数学の問題です。

⇒　2023年（令和5年度）京都府公立入試中期数学の問題PDF

前期同様空白用紙は省いています。

2023年（令和5年度）京都府公立入試中期数学の解説

大問６問は前期と同じで、計算の量も同じくらいだと感じます。
全体的に少し軽めではありますが、
きっちり偏りなく基本は確認されています。

前期での解説で分かることが多いのでここは簡単に済ませておきます。

第１問小問集合

８題ありますので早速進めます。
(1)
　\(\hspace{10pt}\displaystyle -6^2+4\div \left(\,-\frac{2}{3}\,\right)\\
\displaystyle =-36-4\times \frac{3}{2}\\
=-36-6\\
=\underline{　-42　}\)

割り算は逆数の掛け算で処理できることと符号注意です。
(2)
　\(\hspace{10pt}4ab^2\div 6a^2b\times 3ab\\
\displaystyle =\frac{4ab^2\times 3ab}{6a^2b}\\
=\underline{　2b^2　}\)

文字式も計算方法は数字と同じです。
会員サイトのワンポイント「約分の効用」は確認しておきましょう。
（無料メルマガ会員でも見れます。）
(3)
　\(\hspace{10pt}\displaystyle \color{red}{\sqrt{48}}-3\sqrt{2}\times \color{blue}{\sqrt{24}}\\
\displaystyle =\color{red}{4\sqrt{3}}-3\sqrt{2}\times \color{blue}{2\sqrt{6}}\\
=4\sqrt{3}-6\color{magenta}{\sqrt{12}}\\
=4\sqrt{3}-6\times \color{magenta}{2\sqrt{3}}\\
=4\sqrt{3}-12\sqrt{3}\\
=\underline{　-8\sqrt{3}　}\)

素因数分解は確実にして、
暗算はできるだけさけたほうがミスが減ります。
(4)
連立方程式なので一文字消去です。
　\( \begin{cases}
\hspace{4pt} 4x+3y=-7\\
\hspace{4pt} 3x+4y=-14
\end{cases}\)

ここでは加減法で\(\,y\,\)から消去します。
（どちらからでも良いですよ。）
\(\hspace{10pt}16x+12y=-28\\
\underline{-)\,\,9x+12y=-42　}\\
\hspace{14pt}7x\hspace{28pt}=14\\
\hspace{48pt}x=2\)

最初の方程式に戻して、（どれでもいい。）
　\(\begin{eqnarray}\displaystyle
4\times (2)+3y&=&-7\\
3y&=&-15\\
y&=&-5
\end{eqnarray}\)

答え　\(\,\underline{　x=2\,,\,y=-5　}\,\)

(5)
与式が交代式なので条件式から処理しても良いのですが、
与式から整理しておきましょう。
　\(\hspace{10pt}xy^2-x^2y\\
=xy(y-x)\)

ここで
　\(\begin{eqnarray}
xy&=&(\sqrt{5}+3)(\sqrt{5}-3)\\
&=&5-9\\
&=&\color{red}{-4}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
y-x&=&(\sqrt{5}-3)-(\sqrt{5}+3)\\
&=&\color{blue}{-6}
\end{eqnarray}\)
よって与式は
　\(\begin{eqnarray}\displaystyle
xy(y-x)&=&(\color{red}{-4})\times (\color{blue}{-6})\\
&=&\underline{　24　}
\end{eqnarray}\)

直接代入しても答えは出せますが数学しましょうね。
(6)
格子点の数を数えます。
関数\(\hspace{4pt}\displaystyle y=\frac{16}{x}\)

\(\,x\,\)が\(\,16\,\)の約数になるときに\(\,y\,\)も整数になります。
\(\hspace{10pt}x=1\,,\,2\,,\,4\,,\,8\,,\,16\)
関数は原点対象なので第3象限にも同じだけあります。
\(\hspace{10pt}x=-1\,,\,-2\,,\,-4\,,\,-8\,,\,-16\)

答え　\(\,\underline{　10　}個\,\)

もちろんグラフを簡単に描いて確認しながら数えるのが良いです。
(7)
平行線が多く平行四辺形が２つできます。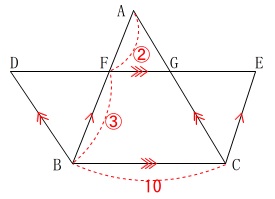相似比から（\(\,\mathrm{△AFG}\,\)∽\(\,\mathrm{△ABC}\,\)）
　\(\begin{eqnarray}\displaystyle
\mathrm{FG}&=&\frac{2}{2+3}\times \mathrm{BC}\\
&=&\frac{2}{5}\times 10\\
&=&\color{blue}{4}
\end{eqnarray}\)
また四角形\(\,\mathrm{DBCG}\,\)と\(\,\mathrm{FBCE}\,\)は平行四辺形なので、
\(\hspace{10pt}\mathrm{DG}=\mathrm{FE}=\color{red}{10}\)
なので
\(\hspace{10pt}\mathrm{DF}=\color{blue}{6}\,,\,\mathrm{GE}=\color{blue}{6}\)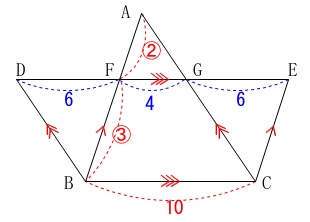足せばでます。
\(\hspace{10pt}\mathrm{DE}=\,6+4+6=\,\underline{　16　}\,(\,\mathrm{cm}\,)\)
(8)
箱ひげ図を書きます。
データは出そろっています。
\(\hspace{10pt}24\,,\,\color{blue}{28}\,,\,\color{blue}{28}\,,\,\color{red}{31}\,,\,\color{red}{33}\,,\,\color{magenta}{35}\,,\,\color{magenta}{39}\,,\,40\)
最小値は\(\,24\,\)、最大値は\(\,40\,\)で、
第１四分位数は\(\,\color{blue}{28}\,\)、中央値は\(\,\color{red}{32}\,\)、第３四分位数は\(\,\color{magenta}{37}\,\)
（それぞれの色の平均値が四分位数になります。）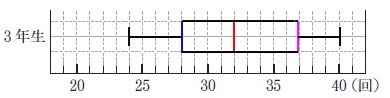

第２問投影図と立体の体積と表面積

\(\,\large{2}\,\)
投影図からはわかりにくいかもしれませんが、
円柱と円錐からできたコマみたいな形です。
(1)
体積からです。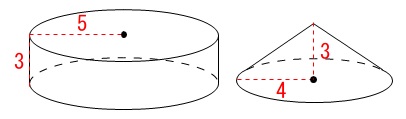求めるたいせき\(\,V\,\)は円柱と円錐の体積の和だから
　\(\begin{eqnarray}\displaystyle
V&=&\pi\,(\,5\,)^2\times 3+\frac{1}{3}\times \pi\,(\,4\,)^2\times 3\\
&=&75\,\pi+16\,\pi\\
&=&\underline{　91\,\pi　}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)
(2)
表面積です。
円柱と円錐の表面積をそれぞれ求めて、
重なる円の部分を２回引いても良いです。

ここでは表に出てくる分だけを書き出して加えます。
円柱の底面から順に下りていきます。
半径５の円を\(\,S_1\,\)としておきます。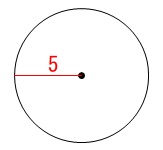\(\hspace{10pt}S_1=\pi\,(5)^2=\,25\,\pi\)
側面の長方形の面積を\(\,S_2\,\)とします。\(\hspace{10pt}S_2=3\times 10\,\pi=\,30\,\pi\)
次に円柱と円錐をつなぐ面の輪の面積を\(\,S_3\,\)とします。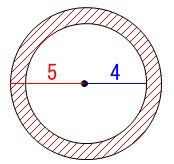\(\hspace{10pt}S_3=\pi\,(5)^2-\pi\,(4)^2=9\,\pi\)
最後に円錐の側面部分の面積を\(\,S_4\,\)とします。おうぎ形ですが母線の長さは\(\,\color{red}{5}\,\)で円周が\(\,\color{blue}{10\,\pi}\,\)に対し、
弧の長さは半径\(\,4\,\)の円周と等しく\(\,\color{red}{8\,\pi}\,\)になっているから、
　\(\begin{eqnarray}\displaystyle
S_4&=&\pi\,(\,5\,)^2\times \frac{8\,\pi}{10\,\pi}\\
&=&25\,\pi\times \frac{4}{5}\\
&=&20\,\pi
\end{eqnarray}\)
※
もちろんですが
\(\hspace{10pt}\displaystyle S_4=\frac{1}{2}\times 8\,\pi\times 5=20\,\pi\)
で求めて良いですよ。

⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

よって求める表面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&S_1+S_2+S_3+S_4\\
&=&25\,\pi+30\,\pi+9\,\pi+20\,\pi\\
&=&\underline{　84\,\pi　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

円錐の展開図は上にあるけど、
円柱の展開図を書いて確認してみて下さい。

第３問確率

\(\,\large{3}\,\)
樹形図で良いです。
(1)
真人さんは\(\hspace{4pt}\color{red}{1}\,,\,\color{red}{9}\,,\,\color{red}{12}\)
有里さんは\(\hspace{4pt}\color{blue}{3}\,,\,\color{blue}{6}\,,\,\color{blue}{11}\)
から１枚ずつ取り出すので全部で９通りになります。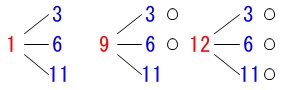真人さんが勝つ（大きい数字を引く）のは
\(\hspace{4pt}\color{red}{9}\,\)のときの\(\,\color{blue}{3}\,,\,\color{blue}{6}\,\)と
\(\hspace{4pt}\color{red}{12}\,\)のときの\(\,\color{blue}{3}\,,\,\color{blue}{6}\,,\,\color{blue}{11}\)
の５通りなので
\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{5}{9}　}}\)
(2)
真人さんが引く袋\(\,\mathrm{X}\,\)に\(\,\color{red}{4}\,\)が加わります。
\(\hspace{4pt}\color{red}{1}\,,\,\color{red}{4}\,,\,\color{red}{9}\,,\,\color{red}{12}\)
有里さんの引く袋\(\,\mathrm{Y}\,\)に１枚\(\,\color{blue}{●}\,\)を加えて勝つ確率を等しくします。
\(\hspace{4pt}\color{blue}{3}\,,\,\color{blue}{6}\,,\,\color{blue}{11}\,,\,\color{blue}{●}\)

\(\,\color{blue}{●}\,\)に入る数字は\(\,\color{blue}{2}\,,\,\color{blue}{5}\,,\,\color{blue}{7}\,,\,\color{blue}{8}\,,\,\color{blue}{10}\,,\,\color{blue}{13}\,\)のどれかです。

引き方は全部で１６通りになるけど引き分けはありません。
勝つ確率を等しくするには、
真人さんが勝つ場合を８通りにすれば良いのです。

\(\,\color{blue}{●}\,\)を加える前を見ると
真人さんが勝つ場合は６通り。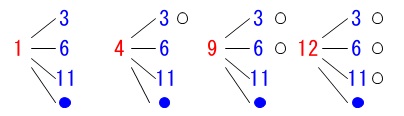あと２通り増えれば等しくなります。
すべての数字を確認しても大した作業ではありません。
\(\hspace{10pt}\underline{　5\,,\,7\,,\,8　}\)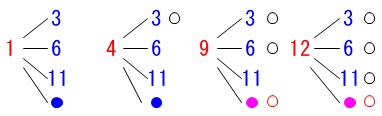確率が等しくなることを考えると、
\(\,4\,\)より大きく\(\,9\,\)より小さい数学が\(\,\mathrm{Y}\,\)に入るときです。

第４問動点と関数問題

\(\,\large{4}\,\)
２点が移動する動点問題ですが、
動点問題の基本通り進めればややこしい計算はありません。

２点\(\,\mathrm{P\,,\,Q}\,\)の動きを見ておくと、
（２点の動く速さは同じです。）
点\(\,\mathrm{P}\,\)は\(\,6\,\)秒間動いて後は止まったままです。
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{18}\,\)秒間動きます。
(1)
正方形の１辺は６なので６秒ごとに変化するので、
\(\hspace{4pt}0\,≦\,x\,≦\,6\)
\(\hspace{4pt}6\,≦\,x\,≦\,12\)
\(\hspace{4pt}12\,≦\,x\,≦\,18\)
それぞれ区間を見ていけば良いです。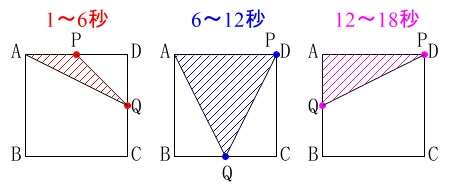\(\,\mathrm{△AQP}\,\)の面積が\(\,y\,\)なので、
ⅰ）
\(\hspace{4pt}0\,≦\,x\,≦\,6\,\)のとき、
底辺\(\,x\,\)、高さ\(\,x\,\)の三角形だから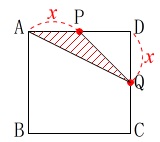\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x^2\)
ⅱ）
\(\hspace{4pt}6\,≦\,x\,≦\,12\,\)のとき、
底辺\(\,6\,\)、高さ\(\,6\,\)の三角形だから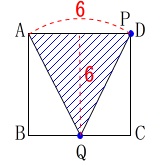面積は一定で
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\times 6\times 6\,=\,18\)
ⅲ）
\(\hspace{4pt}12\,≦\,x\,≦\,18\,\)のとき、
底辺\(\,\mathrm{AD}=6\,\)、高さ\(\,(\,\mathrm{AQ}=\color{red}{18-x}\,)\,\)の三角形だから
（\(\,\mathrm{D→C→B→A}\,\)で\(\,18\,\)だから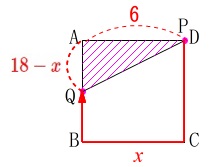）\(\begin{eqnarray}
y&=&\frac{1}{2}\times 6\times (\,18-x\,)\\
&=&54-3\,x
\end{eqnarray}\)

ここでは関数をだす必要はありませんが、
やっておいても大した時間はかかりません。

\(\,x=1\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (\,1\,)^2\\
&=&\underline{　\frac{1}{2}　}
\end{eqnarray}\)

グラフは放物線、定直線、傾きが負の直線がつながったものです。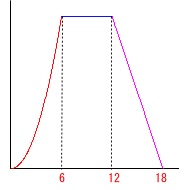\(\hspace{10pt}\underline{　（ウ）　}\)
(2)
正方形の対角線の交点が\(\,\mathrm{R}\,\)で、
\(\,\mathrm{△RQD}\,\)と\(\,\mathrm{△AQD}\,\)の面積が等しくなるときです。
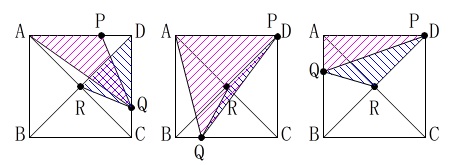おおよその予想はできます。
はっきり分かるのは\(\,6\,\)秒から\(\,12\,\)秒までの間に、
面積が等しくなることはないということです。
（\(\,\mathrm{△RQD}\,\)が\(\,18\,\)になることはない。）

関数の問題なので関数で処理しましょう。
ⅰ）
\(\hspace{4pt}0\,＜\,x\,≦\,6\,\)のとき、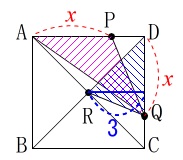\(\hspace{10pt}\displaystyle \mathrm{△APQ}=\frac{1}{2}\,x^2\)
\(\,\mathrm{△RQD}\,\)の面積は底辺が\(\,x\,\)で高さが\(\,\color{blue}{3}\,\)なので
\(\hspace{10pt}\displaystyle \mathrm{△RQD}=\frac{3}{2}\,x\)
面積が等しくなるのでは
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\,x^2&=&\frac{3}{2}\,x\\
x^2-3x&=&0\\
x(x-3)&=&0\\
x&=&0\,,\,3
\end{eqnarray}\)
\(\,x=0\,\)は範囲にないので\(\,x=3\,\)のみ。
ⅱ）
\(\hspace{4pt}12\,≦\,x\,≦\,18\,\)のとき、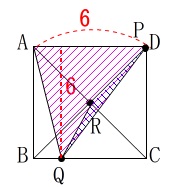明らかに面積が等しくなる事はありません。
ⅲ）
\(\hspace{4pt}12\,≦\,x\,≦\,18\,\)のとき、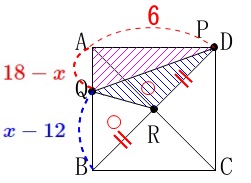\(\hspace{4pt}\mathrm{△AQP}=-3x+54\)
※(1)を見直しておいて下さい。

点\(\,\mathrm{R}\,\)は線分\(\,\mathrm{BD}\,\)の中点なので、
\(\,\mathrm{△RQD}\,\)の面積は\(\,\mathrm{△BDQ}\,\)の半分です。
\(\,\mathrm{△BDQ}\,\)の面積は底辺が線分\(\,\mathrm{QB}\,\)で
\(\begin{eqnarray}
\mathrm{QB}&=&\mathrm{AB-AQ}\\
&=&6-(18-x)\\
&=&\color{blue}{x-12}
\end{eqnarray}\)
高さは\(\,\mathrm{AD=\color{red}{6}}\,\)なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△RQD}&=&\frac{1}{2}\times \mathrm{△BDQ}\\
&=&\frac{1}{2}\times \frac{1}{2}\times \mathrm{QB}\times \mathrm{AD}\\
&=&\frac{1}{4}\times (\color{blue}{x-12})\times 6\\
&=&\frac{3}{2}\,(x-12)
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△AQP}&=&\mathrm{△RQD}\\
-3x+54&=&\frac{3}{2}\,(x-12)\\
-6x+108&=&3x-36\\
-9x&=&-144\\
x&=&16
\end{eqnarray}\)
\(\hspace{4pt}12\,≦\,x\,≦\,18\,\)の場合なので
\(\hspace{4pt}x=16\)は適しています。

答え\(\hspace{10pt}x=\underline{　3\,,\,16　}\)

ⅲ）
\(\hspace{4pt}12\,≦\,x\,≦\,18\,\)のときですが、
図形的に見えると点\(\,\mathrm{R}\,\)が対角線の交点であることから、
\(\hspace{4pt}\mathrm{△AQD=△QBR=△RQD}\)
のときなので線分\(\,\mathrm{AB}\,\)を\(\,\color{red}{2}:\color{blue}{4}\,\)に分けるときです。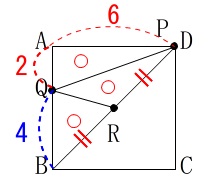二度目に等しくなるのが\(\,16\,\)秒後というのは簡単だったのではないでしょうか。

きれいな数値できっちり関数を理解しているか、
利用できるかを問うてくる良い問題ですね。

第５問平面図形

\(\,\large{5}\,\)
円と相似の利用です。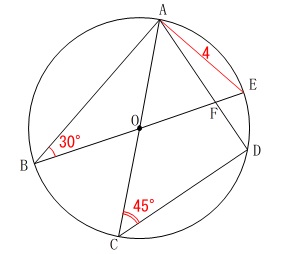条件を図に書き込むと割と早く答えが出るので簡単に済ませましょう。
一気に解決しますが順に見ていきます。
(1)
円\(\,\mathrm{O}\,\)の直径を求めます。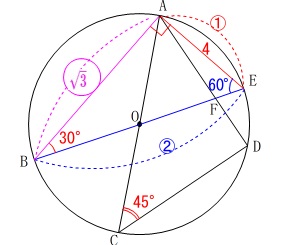\(\,\mathrm{△ABE}\,\)は三角定規なので
\(\hspace{4pt}\mathrm{AE:BE:AB}=\color{red}{1}:\color{blue}{2}:\color{magenta}{\sqrt{3}}\)

円の直径は\(\,\mathrm{AE}\,\)の\(\,2\,\)倍になります。
\(\hspace{10pt}\mathrm{AE:BE:AB}=\color{red}{4}:\color{blue}{8}:\color{magenta}{4\sqrt{3}}\)

答え\(\hspace{4pt}\underline{　8　}(\,\mathrm{cm}\,)\)
(2)
線分\(\,\mathrm{EF}\,\)の長さです。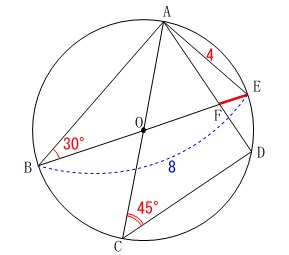相似が利用できそうですが、
角度を使っていないところがあるので見ていきます。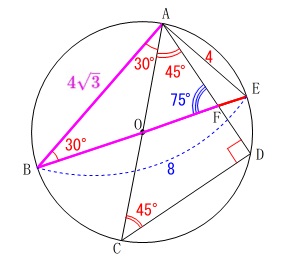他にも分かる角度はたくさんありますが、
とりあえず、\(\,\mathrm{△BAF}\,\)は二等辺三角形と分かったところで止めておきます。
　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&\mathrm{BE-BF}\\
&=&\underline{　8-4\sqrt{3}　}(\,\mathrm{cm}\,)
\end{eqnarray}\)
(3)
線分と交点が追加されます。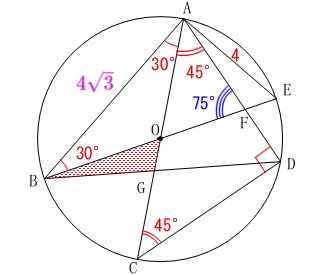このときの\(\,\mathrm{△OBG}\,\)の面積を求めます。

気持ちの良い誘導が(2)にあります。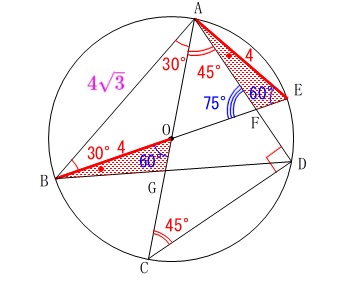半径や円周角の定理などから
　\(\,\mathrm{△OBG}\,\)≡\(\,\mathrm{△EAF}\,\)
が言えるのでどちらでも良いですが、
\(\,\mathrm{△EAF}\,\)の面積を求める事にします。

点\(\,\mathrm{A}\,\)から\(\,\mathrm{BE}\,\)に垂線を下ろして、
交点を\(\,\mathrm{H}\,\)とすると三角定規ができて
\(\hspace{10pt}\mathrm{AH}=\color{blue}{2\sqrt{3}}\)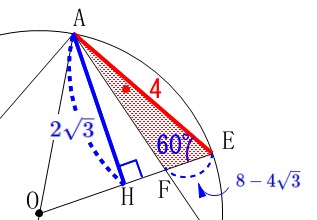(2)から底辺\(\,\mathrm{EF}=\color{blue}{8-4\sqrt{3}}\,\)は求まっているので
　\(\begin{eqnarray}\displaystyle
\mathrm{△OBG}&=&\mathrm{△EAF}\\
&=&\frac{1}{2}\times (8-4\sqrt{3})\times 2\sqrt{3}\\
&=&\sqrt{3}\times (8-4\sqrt{3})\\
&=&\underline{　8\sqrt{3}-12　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

点\(\,\mathrm{B}\,\)から\(\,\mathrm{AC}\,\)に垂線を下ろしても同じです。
（自分でやってみて下さい。）

第６問規則性問題

\(\,\large{6}\,\)
規則性の問題です。
タイル\(\,\mathrm{\color{red}{A}}\,\)については簡単ですが問題はタイル\(\,\mathrm{\color{blue}{B}}\,\)でしょう。
正方形(\(\,\mathrm{\color{red}{A}}\,\))と線(\(\,\mathrm{\color{blue}{B}}\,\))に換えて見ていきます。
(1)
タイル\(\,\mathrm{A}\,\)です。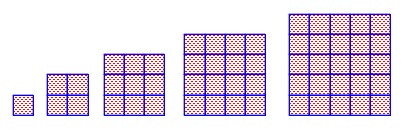数えても良いです。
\(\hspace{10pt}1\,,\,4,,\,9\,,\,16\,,\,\cdots \,n^2\)
平方数（奇数の和）として増えていくので\(\,5\,\)番目は
　\(\hspace{10pt}5^2=\,\underline{　25　}枚\)
※
前期の規則性でも説明しているので、
奇数の和が平方数になることは確認しておきましょう。
(2)
タイル\(\,\mathrm{B}\,\)の数です。
これは見方が分かれると思います。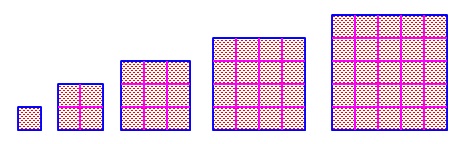周囲を除いた部分（中にあるタイル）を数えるか、
重なりとみて省くかで少し変わってきます。
（もちろん\(\,12\,\)番目の図形を書いて数えても良いです。）

どっちからいきましょう？

6-(2)間のタイルを数える方法

先に数える方法でいきましょうか。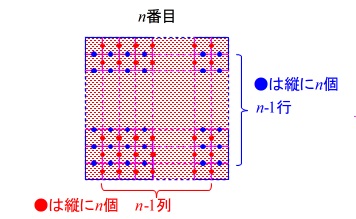\(\,n\,\)番目の図形では、
周囲の辺（タイル\(\,\mathrm{\color{blue}{B}}\,\)）は\(\,4n\,\)あります。
間にある辺は縦の\(\,\color{red}{n}\,\)個が横に\(\,\color{red}{n-1}\,\)列あり、
横に\(\,\color{blue}{n}\,\)個が\(\,\color{blue}{n-1}\,\)行あります。

合計でタイル\(\,\mathrm{B}\,\)は
　\(\hspace{10pt}4n+\color{red}{n}(\color{red}{n-1})+\color{blue}{n}(\color{blue}{n-1})\\
=2n^2+2n\\
=2n(n+1)\)
となります。

よって、\(\,12\,\)番目の図形では
　\(\hspace{10pt}2\times 12\times (12+1)\\
=24\times 13\\
=\underline{　312　}枚\)

6-(2)重なるタイルを引く方法

次に元は一番目の図形が\(\,n\,\)番目までバラバラで、
それが重なってできていると見ておきます。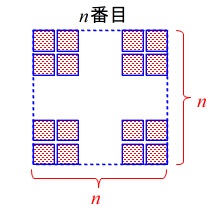重なりがないときの辺の数（タイル\(\,\mathrm{B}\,\)）は、
タイル\(\,\mathrm{A}\,\)の数の\(\,4\,\)倍（正方形の４辺）になるので\(\,4n^2\,\)枚。

これから重なる部分は２回数えていることになるのでその分を引きます。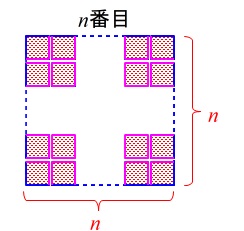重なる部分は上の方法で数えても良いですが、
すべての辺から周囲の辺\(\,\color{blue}{4n}\,\)を引くとでます。
ただし、重なる部分は全部無くすのではありません。

２本の辺が重なる辺の半分は残すことになるので、
\(\hspace{10pt}\displaystyle \frac{4n^2-4n}{2}=\color{red}{2n^2-2n}\)

これに周囲の辺の\(\,\color{blue}{4n}\,\)を加えて
　\(\hspace{10pt}\color{blue}{4n}+(\color{red}{2n^2-2n})\\
=2n^2+2n\)

よって、\(\,12\,\)番目の図形のタイル\(\,\mathrm{B}\,\)の数は
　\(\hspace{10pt}2\times 12^2+2\times 12\\
=288+24\\
=\underline{　312　}枚\)

似たようなことやっているので「間を数える」で良いのではないか？と思われるでしょう。
重なりの図形の規則性の場合、
重なりを引くことを考えることで上手くいくことが多いので示しておきました。
(3)
これは方程式を解くだけです。
タイル\(\,\mathrm{B}\,\)の方が多いので
　\(\begin{eqnarray}\displaystyle
2n(n+1)-n^2&=&360\\
2n^2+2n-n^2-360&=&0\\
n^2+2n-360&=&0\\
(n+20)(n-18)&=&0\\
n&=&-20\,,\,18
\end{eqnarray}\)
\(\,n\,\)は自然数なので
\(\hspace{10pt}n=\underline{　18　}\)

定数項が大きい数の場合の因数分解の要領も、
前期で示していますので確認しておくと良いです。

かなり手抜きと言われそうですが以上です。

⇒　2023年（令和5年度）京都府公立入試前期数学の問題と解説

前期がかなり後期の参考になるのは良くあることですよ。
後期を受験する場合は前期の確認を忘れずにしておくと対策に役立ちます。

⇒　京都府公立高校入試数学の過去問と解答解説

京都府の公立入試は高校に進学してからのことを考えた選抜をしていると思えます。
入試本番での逆転は厳しいので普段から基礎の徹底を心来がけておきましょう。
基本問題という意味だけはなく、基本的な作業もです。