２０２３年（令和５年）度奈良県公立高校入試の数学の問題と解説です。
大問４問の構成は昨年度と変わりありません。
中学で学ぶ数学全範囲の定義からの基礎を重視した問題なので、
簡単そうで差がつく問題だといった印象です。
作図もありますが方法は人によって違いが出るでしょう。
2023年（令和5年）度奈良県公立高校入試数学の問題
２０２３年（令和５年）度奈良県公立高校入試数学の問題です。
元は２ページが１つになっていますが１ページずつに分けておきました。
２ページずつの問題を見たい場合は奈良県の公式ページでご確認下さい。
（見え方が違うだけで問題の内容は同じです。）
※
２ページにまたがる問題があるので載せておきます。
2023年（令和5年）度奈良県公立高校入試数学の解説
令和５年度奈良県公立高校入試数学の解説です。
大問４つは少なく感じますがボリュームは十分ありますよ。
なので早速解説していきます。
第１問小問集合
\(\large{\color{black}{\fbox{1}}}\)
(1)計算です。
①
\(\hspace{10pt}7-(-6)\\
=7+6\\
=\underline{ 13 }\)
負の数の引き算は足し算と同じだというのは良いでしょう。
②
\(\hspace{10pt}15+(-4)^2\div (-2)\\
=15+16\div (-2)\\
=15-8\\
=\underline{ 7 }\)
計算順序を間違えなければ割り算を分数処理しなくても良いです。
③
\(\hspace{10pt}(x+2)(x-5)-2(x-1)\\
=x^2-3x-10-2x+2\\
=\underline{ x^2-5x-8 }\)
普通に展開して整理するだけです。
④
\(\hspace{10pt}\sqrt{2}\times \sqrt{6}-\sqrt{27}\\
=\sqrt{12}-3\sqrt{3}\\
=2\sqrt{3}-3\sqrt{3}\\
=\underline{ -\sqrt{3} }\)
２行目はなくても良いくらい無理数計算に慣れておくのは良いことです。
ただし、素因数分解は確実にすることをお勧めします。
(2)
連立方程式を解きます。
\( \begin{cases}
\hspace{4pt} x+4y=5 ･･･①\\
\hspace{4pt} 4x+7y=-16 ･･･②
\end{cases}\)
基本通り一文字消去ですが\(\,x\,\)の方が消しやすいですね。
第１方程式\(\,①\,\)を両辺４倍します。
\(\hspace{14pt}4x+16y=20\\
\underline{-)\,4x+\hspace{6pt}7y=-16 }\\
\hspace{41pt}9y=36\\
\hspace{45pt}y=4\)
\(\,①\,\)に戻して
\(\begin{eqnarray}\displaystyle
x+4\times (4)&=&5\\
x+16&=&5\\
x&=&-11
\end{eqnarray}\)
答え\(\hspace{10pt}\underline{ x=-11\,,\,y=4 }\)
基本通り進めるなら求め方は何でも良いです。
(3)
２次方程式を解きます。
\(\hspace{10pt}x^2+5x+1=0\)
因数分解できないので解の公式です。
\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{5^2-4\cdot 1\cdot 1}}{2\times 1}\\
&=&\underline{\underline{ \frac{-5\pm \sqrt{21}}{2} }}
\end{eqnarray}\)
※
ルートの中の「\(\,\cdot\,\)」は掛け算の意味です。
⇒ ２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方
解の公式は導く事より使うこと優先で良いです。
解答時間短縮のためにも必ず覚えておきましょう。
(4)
最も小さくなるのは数直線で一番左に来る数です。
（ここでは絶対値が大きい負の数。）
\(\hspace{10pt}a\,＜\,0\,,\,b\,＜\,0\)
答え\(\hspace{10pt}\underline{ a+b }\)
\(\,a-b\,\)は\(\,b\,\)が負の数なので\(\,-b\,\)の部分はプラス側に移動する。
\(\,a\,b\,\)は負の数同士の掛け算なので正の数になります。
\(\displaystyle \frac{a}{b}=a\times \frac{1}{b}\,\)も同じです。
\(\,a+bは\,\)負の数と負の数の和なので数直線上で一番左になります。
(5)
相似比が\(\,2:3\,\)のとき、
体積比は\(\,8:27\,\)になります。
求める体積を\(\,V\,\)とすると
\(\begin{eqnarray}\displaystyle
8:27&=&24:V\\
8\,V&=&24\times 27\\
V&=&\underline{ 81 }\,(\,\mathrm{cm^3}\,)
\end{eqnarray}\)
相似比が\(\,\color{red}{a}:\color{blue}{b}\,\)のとき体積比は\(\,\color{red}{a^3}:\color{blue}{b^3}\,\)です。
(5)
確率の問題ですが先ずは表と裏が何回出たか求めなければなりません。
表が\(\,x\,\)回出たとすると裏は\(\,3-x\,\)回出たことになります。
（３回投げるから）
原点にあるということは移動が\(\,0\,\)だったということなので
\(\begin{eqnarray}\displaystyle
x+(-2)(3-x)&=&0\\
x-6+2x&=&0\\
x&=&2
\end{eqnarray}\)
つまり３回投げて表が２回出る確率を求めます。
樹形図で良いですよ。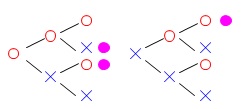
答え\(\hspace{10pt}\displaystyle \underline{\underline{ \frac{3}{8} }}\)
方程式にしなくても樹形図書いて８通り調べれば良いだけです。
(7)
作図です。
条件を満たす順に作図手順を踏めばいいです。
【条件】\(\,①\,\)から、
点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{AB}\,\)の垂直二等分線上にある。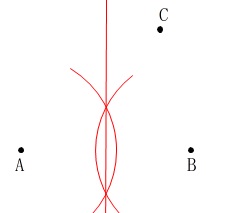
【条件】\(\,②\,\)から
点\(\,\mathrm{P}\,\)は\(\,\mathrm{C}\,\)を通り\(\,\mathrm{AB}\,\)に平行な直線上にある。
ここで点\(\,\mathrm{C}\,\)を通る平行線の引き方は垂線か平行線かで分かれますね。
\(\,①\,\)で引いた直線に\(\,\mathrm{C}\,\)から垂線を引くか、
平行四辺形を利用するか、です。
平行四辺形にしておきます。
イメージとしては平行四辺形\(\,\mathrm{ABCD}\,\)を描く感じです。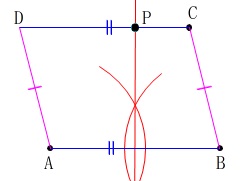
作図としてはすべての線分はいらないので、
コンパスで平行四辺形を描いていますと見せれば良いです。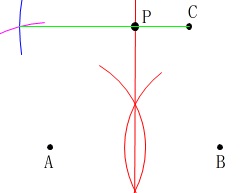
点\(\,\mathrm{C}\,\)から垂線引いた方が作図っぽく見えるかもしれないですね。
（採点側の問題です。）
(8)
累積相対度数のグラフから読み取れることを選びます。
１年生と３年生では総人数が違うことに注意しましょう。
グラフでは見にくいという人は累積相対度数分布表で見ると良いですが、
１年生７５人の４２％は\(\,31.5\,\)人と数がおかしいことに気がつきますので、
グラフから大まかに読み取るしかないと分かります。
適切なものを全て選ぶのですべて読み取ります。
ア
中央値は累積相対度数\(\,0.50\,\)を含む階級を見れば良いので、
１年生の方が小さい。×
イ
２０分未満の生徒は、
１年生６６％、３年生５２％でいずれも半分以上です。○
ウ
２５分未満の生徒は、
１年生、３年生ともに累積相対度数は同じですが、
度数合計が違うので度数（人数）は違います。×
エ
２５分以上３０分未満の相対度数は、
１年生\(\,0.04\,\)で３年生\(\,0.14\,\)なので、
度数合計から見ても３年生の方が多い。○
（累積相対度数から１つ前の累積相対度数を引けばその階級の相対度数が出ます。）
オ
度数は考えず、累積相対度数\(\,0.76\,\)までは１年生の方が短いので、
傾向からすれば１年生の方が短い。○
答え\(\hspace{4pt}\underline{ イ\,,\,エ\,,\,オ }\)
人数が整数で出なかった、そんなことあるのか？
相対度数は度数の一番多い階級で最小単位を調整するのでないわけではありません。
第２問図形の移動範囲
\(\large{\color{black}{\fbox{2}}}\)
円や正方形が通過できる範囲が限られる、という問題です。
ある程度は示すけど条件は自分で読み取っておいて下さい。
(1)
角度と角の二等分線の定義と長さを求める問題です。
①
\(\,\mathrm{∠PXQ}\,\)が\(\,45°\,\)なので内角から出ます。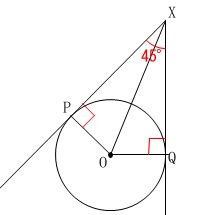
\(\begin{eqnarray}
\mathrm{∠POQ}&=&360°-(90°+90°+45°)\\
&=&360^{\circ}-225^{\circ}\\
&=&\underline{ 135^{\circ} }
\end{eqnarray}\)
②
\(\,\mathrm{△OPX}\,\)と\(\,\mathrm{△OQX}\,\)は合同なので、
\(\hspace{10pt}\mathrm{∠PXO=∠QXO}\)
線分\(\,\mathrm{XR}\,\)は\(\,\mathrm{∠YXZ}\,\)の角の二等分線です。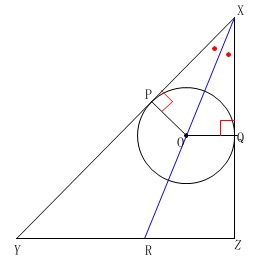
角の二等分線は、
二辺から等しい距離にある点の集まりです。
答え\(\hspace{4pt}\underline{ 辺\,\mathrm{XY}\,と辺\,\mathrm{XZ}\,から等しい距離にある点。 }\)
ここでは線分について聞かれていないので点の説明になります。
③
円\(\,\mathrm{O}\,\)の半径は\(\,2\,\)です。
直角三角形はありますが直接三平方の定理は使えません。
\(\,\mathrm{YZ}\,\)と平行な線を加えると直角二等辺三角形ができます。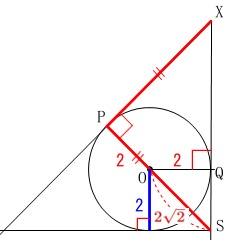
１辺が２の正方形の対角線は\(\,\color{red}{2\sqrt{2}}\,\)なので、
直角二等辺三角形\(\,\mathrm{XPS}\,\)から
\(\begin{eqnarray}\displaystyle
\mathrm{XP}&=&\mathrm{PS}\\
&=&\mathrm{PO+OS}\\
&=&\underline{ 2+2\sqrt{2} }(\,\mathrm{cm}\,)
\end{eqnarray}\)
直角三角形に円が内接するとき正方形ができることを覚えておくと良いです。
直角二等辺三角形\(\,\mathrm{XQT}\,\)から求めても同じようなものです。
\(\begin{eqnarray}\displaystyle
\mathrm{XP}&=&\mathrm{XQ}\\
&=&\mathrm{TQ}\\
&=&\mathrm{TO+OQ}\\
&=&2\sqrt{2}+2
\end{eqnarray}\)
(2)
今度は正方形が通過する範囲です。
①
会話のヒントがなければかなり悩むと思います。
「点\(\,\mathrm{X}\,\)は点\(\,\mathrm{A}\,\)を中心として２点\(\,\mathrm{B\,,\,D}\,\)を通る円周上にある。」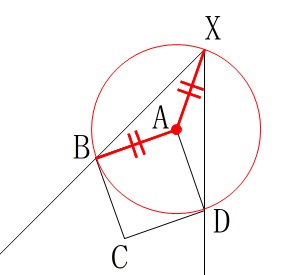
半径は等しいので線分\(\,\mathrm{AB}\,\)と等しい。
答え\(\hspace{4pt}\underline{ イ }\)
②
正方形が通過した部分の面積ですが、
通過できない面積を考えます。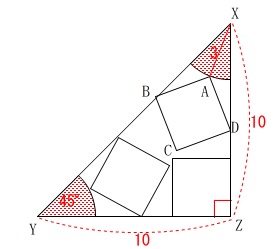
直角の部分では正方形がきれいにはまりますが、
右上の赤い部分は頂点\(\,\mathrm{A}\,\)は\(\,\mathrm{X}\,\)に届きません。
（左下も同じです。）
求める面積\(\,S\,\)は直角二等辺三角形から赤い部分を除いた部分で、
正方形の１辺（半径）が３なので
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times 10\times 10-\left\{\,\color{red}{\pi\,(3)^2\times \frac{45}{360}}\,\right\}\times 2\\
&=&50-9\,\pi\times \frac{1}{4}\\
&=&\underline{\underline{ 50-\frac{9}{4}\,\pi }}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)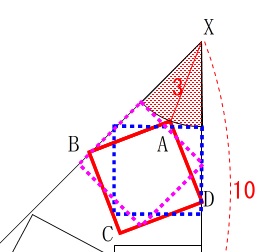
イメージだけでは\(\,\mathrm{X}\,\)を中心のおうぎ形がとらえにくいでしょう。
問題がヒントをくれるているのでありがたいです。
第３問関数
\(\large{\color{black}{\fbox{3}}}\)
条件がしっかり与えられているので取り組みやすいです。
関数と\(\,x\,\)座標が分かっているのでグラフ上に示しておくと良いです。
\(\hspace{4pt}\mathrm{A}\,(\,-4\,,\,16a\,)\,,\,\mathrm{B}\,(\,2\,,\,4a\,)\)
\(\hspace{4pt}\mathrm{C}\,(\,-4\,,\,-8\,)\,,\,\mathrm{D}\,(\,2\,,\,-2\,)\)
(1)
最大値に気をつければ問題ないでしょう。
点\(\,\mathrm{D}\,\)の\(\,y\,\)座標は値域には関係ありません。
答え\(\hspace{4pt}\underline{ -8\,≦\,y\,≦\,0 }\)
(2)
２点\(\,\mathrm{C\,,\,D}\,\)を通る直線です。
\(\hspace{4pt}\mathrm{C}\,(\,-4\,,\,-8\,)\)
\(\hspace{4pt}\mathrm{D}\,(\,2\,,\,-2\,)\)
答え\(\hspace{4pt}\underline{ y=x-4 }\)
傾きと切片を求めれば良いので連立方程式でも良いですが、
直線の式はできるだけ短時間で求められるようになっておきましょう。
(3)
関数の比例定数が正なのでグラフから直感的にも分かります。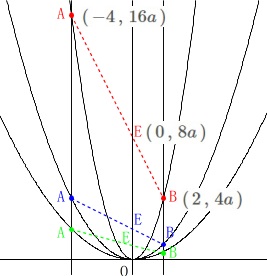
一応説明しておきます。
\(\hspace{4pt}\mathrm{A}\,(\,-4\,,\,16a\,)\)
\(\hspace{4pt}\mathrm{B}\,(\,2\,,\,4a\,)\)
ア
比例定数が大きくなるにつれて、
傾きはより右下がりになるので小さくなります。○
\(\begin{eqnarray}\displaystyle
(\,傾き\,)&=&\frac{4a-16a}{2-(-4)}\\
&=&-2\,a
\end{eqnarray}\)
１つ選べば良いので答えです。
答え\(\hspace{4pt}\underline{ ア }\)
イ
比例定数\(\,a\,\)が大きくなるにつれて、
線分\(\,\mathrm{AB}\,\)の長さは大きくなっていきます。
\(\begin{eqnarray}
\mathrm{AB}&=&\sqrt{\{\,2-(-4)\,\}^2+(\,4a-16a\,)^2}\\
&=&\sqrt{6^2+144a^2}
\end{eqnarray}\)
ウ
比例定数\(\,a\,\)が大きくなるにつれて、
\(\,\mathrm{△OAB}\,\)の面積は大きくなっていきます。
\(\begin{eqnarray}\displaystyle
\mathrm{△OAB}&=&\frac{1}{2}\times 8a\times (-4)+\frac{1}{2}\times 8a\times 2\\
&=&24\,a
\end{eqnarray}\)
※
点\(\,\mathrm{E}\,\)の座標は\(\,(\,0\,,\,8a\,)\,\)です。
エ
\(\,x\,\)座標は固定されているので、
線分比\(\,\mathrm{AE:EB}\,\)は一定です。
(4)
直線\(\,\mathrm{OD}\,\)は定まり、
四角形\(\,\mathrm{ACDB}\,\)は台形なので文字式で簡単に処理できます。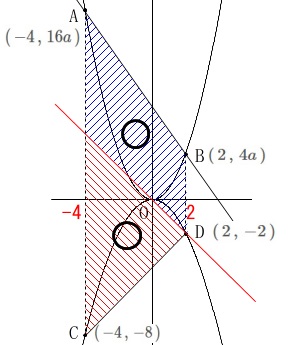
台形を三角形と四角形で等しく分ければ良いのです。
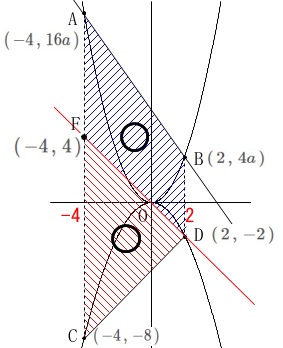直線\(\,\mathrm{OD}\,\)の式は\(\hspace{4pt}y=-x\,\)なので、
直線\(\,\mathrm{AC}\,\)との交点\(\,\mathrm{F}\,\)は\(\,\mathrm{(\,-4\,,\,4\,)}\,\)です。
台形\(\,\mathrm{ACDB}\,\)の面積が\(\,\mathrm{△DFEC}\,\)の２倍になればいいので
\(\hspace{10pt}\mathrm{BD}=4a-(-2)=\color{red}{4\,a+2}\)
\(\hspace{10pt}\mathrm{AC}=16a-(-8)=\color{red}{16\,a+8}\)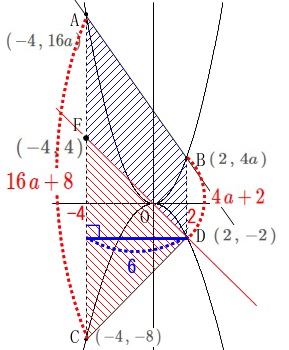
高さは\(\,\color{blue}{6}\,\)だから、
（\(\,y\,\)座標の差から\(\,\mathrm{FC}=4-(-8)=12\,\)より）
\(\begin{eqnarray}\displaystyle
(\,台形\,\mathrm{ACDB}\,)&=&2\times \mathrm{\color{red}{△DFC}}\\
\frac{\mathrm{BD+AC}}{2}\times 6&=&2\times \color{red}{\frac{1}{2}\times \mathrm{FC}\times 6}\\
\frac{(4a+2)+(16a+8)}{2}\times 6&=&2\times \frac{1}{2}\times 12\times 6\\
20\,a+10&=&24\\
20\,a&=&14\\
a&=&\underline{\underline{ \frac{7}{10} }}
\end{eqnarray}\)
\(\,\mathrm{△DFC}\,\)の面積は一定なので、
それぞれの面積を別々に出してから計算しても良いです。
第４問平面図形
\(\large{\color{black}{\fbox{4}}}\)
平面図形の証明から長さ、面積までの総合問題です。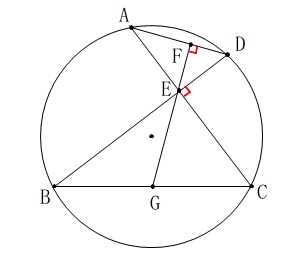
直角三角形と相似がたくさんあるので補助線は少なくしておきたいところです。
(1)
相似の証明です。
\(\hspace{10pt}\mathrm{△AEF}\,\)∽\(\,\mathrm{△BCE}\,\)
図の中で終わらせておきましょう。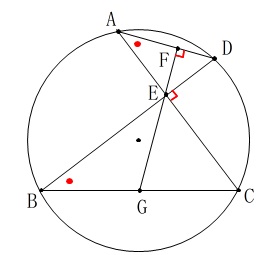
仮定の垂直と、同一弧の円周角から、
「２組の角がそれぞれ等しい。」
が相似条件になります。
⇒ 中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント
ルールさえ守っていれば書き方は自分の書きやすい方法で良いですよ。
(2)
\(\,\mathrm{∠BGE}\,\)を\(\,a\,\)を用いて表します。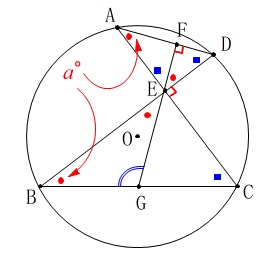
直角三角形に垂線を下ろしているので、
\(\hspace{10pt}\mathrm{△AEF}\,\)∽\(\,\mathrm{△EDF}\,\)
対応する角は等しいから
\(\hspace{10pt}\mathrm{∠EAF}=\mathrm{∠DEF}=\color{red}{a^{\circ}}\)
また対頂角は等しいから
\(\hspace{10pt}\mathrm{∠DEF}=\mathrm{∠GEB}=\color{red}{a^{\circ}}\)
三角形の内角の和から
\(\begin{eqnarray}
\mathrm{∠BGE}+a^{\circ}+a^{\circ}&=&180^{\circ}\\
\mathrm{∠BGE}&=&\underline{ 180°-2\,a^{\circ} }
\end{eqnarray}\)
ちなみに\(\,\mathrm{△CBE}\,\)と\(\,\mathrm{△DAE}\,\)も相似です。
(3)
長さが出てきます。
\(\hspace{10pt}\mathrm{DE}=3\,,\,\mathrm{AE}=4\,,\,\mathrm{BE}=8\)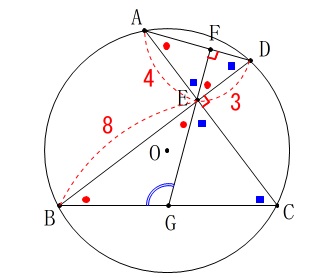
※長さの単位は\(\,\mathrm{cm}\,\)です。
①
\(\,\mathrm{△CEG}\,\)の面積を求めます。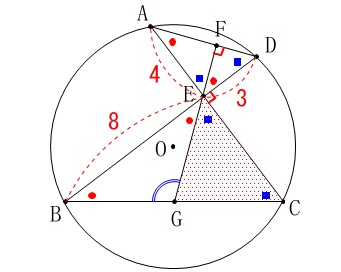
点\(\,\mathrm{E}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろしても相似ができるので良いとは思いますが、
直角三角形\(\,\mathrm{BEC}\,\)の面積を利用します。
（補助線を必要としない方針）
直角三角形であり、
\(\hspace{10pt}\,\mathrm{△CBE}\,\)∽\(\,\mathrm{△DAE}\,\)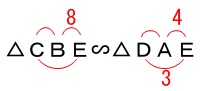
なので
\(\begin{eqnarray}
\mathrm{BE:AE}&=&\mathrm{CE:DE}\\
8:4&=&\mathrm{CE}:3\\
\mathrm{CE}&=&\color{blue}{6}
\end{eqnarray}\)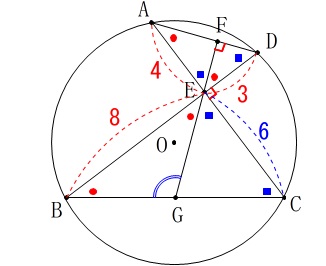
直角三角形なので
\(\begin{eqnarray}
\mathrm{\color{magenta}{△CEB}}&=&\frac{1}{2}\times \mathrm{CE}\times \mathrm{BE}\\
&=&\frac{1}{2}\times 6\times 8\\
&=&\color{magenta}{24}
\end{eqnarray}\)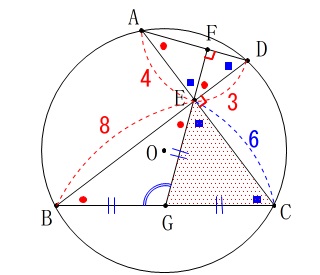
\(\,\mathrm{△GBE}\,\)と\(\,\mathrm{△GCE}\,\)は二等辺三角形で１辺を共通にしているので、
\(\hspace{10pt}\mathrm{GE=GB=GC}\)
だから求める\(\,\mathrm{△CEG}\,\)の面積は\(\,\mathrm{△CEB}\,\)の半分です。
\(\begin{eqnarray}
\mathrm{△CEG}&=&\frac{1}{2}\times \mathrm{\color{magenta}{△CEB}}\\
&=&\frac{1}{2}\times \color{magenta}{24}\\
&=&\underline{ 12 }\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)
②
円\(\,\mathrm{O}\,\)の半径を求めますが、
半径となる線分がないのでここで補助線を入れます。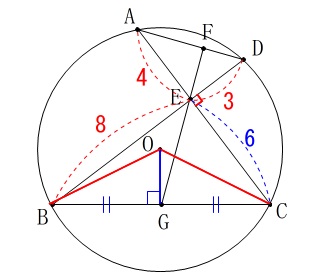
半径となる線分がなかったので線分\(\,\mathrm{OB}\,\)を引きます。
線分\(\,\mathrm{OC}\,\)も半径となり、
点\(\,\mathrm{G}\,\)が\(\,\mathrm{BC}\,\)の中点だから\(\,\mathrm{OG}\,\)⊥\(\,\mathrm{BC}\,\)です。
線分\(\,\mathrm{BC}\,\)は直角三角形の斜辺で三平方の定理から
\(\hspace{10pt}\mathrm{BC}=10\)
点\(\,\mathrm{G}\,\)は線分\(\,\mathrm{BC}\,\)中点だから
\(\hspace{10pt}\mathrm{BG}=\color{blue}{5}\)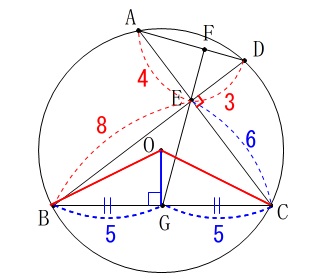
線分\(\,\mathrm{OG}\,\)の長さがあれば三平方の定理で良いですが分かっていません。
相似を考えると円周角と中心角の関係から、
\(\hspace{10pt}\mathrm{∠BOC}=2\times \mathrm{∠BAC}\)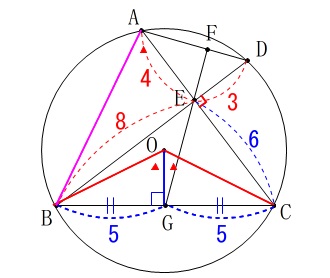
線分\(\,\mathrm{OG}\,\)は二等辺三角形の頂角を２等分しているので
\(\hspace{4pt}\mathrm{∠BAC}=\mathrm{∠BOG}\)だから
\(\hspace{10pt}\mathrm{\color{red}{△ABE}}\,\)∽\(\,\mathrm{\color{blue}{△OBG}}\,\)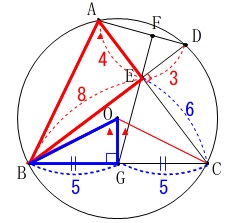
線分\(\,\mathrm{AB}\,\)は直角三角形\(\,\mathrm{ABE}\,\)の斜辺で、
三平方の定理から（正の平方根を計算して）
\(\begin{eqnarray}
\mathrm{AB}&=&\sqrt{\mathrm{AE^2+BE^2}}\\
&=&\sqrt{4^2+8^2}\\
&=&\sqrt{16+64}\\
&=&\sqrt{80}\\
&=&\color{magenta}{4\sqrt{5}}
\end{eqnarray}\)
※
\(\,1:2:\sqrt{5}\,\)から\(\,\mathrm{AB=4\sqrt{5}}\,\)としても良いです。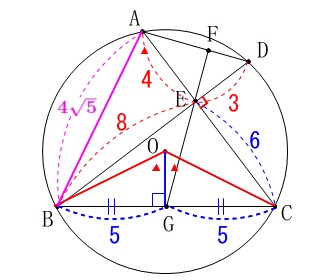
これで対応する辺が分かったので、
相似比から求まります。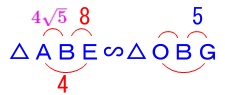
\(\begin{eqnarray}
\mathrm{AB:OB}&=&\mathrm{BE:BG}\\
\color{magenta}{4\sqrt{5}}:\mathrm{OB}&=&\color{red}{8}:\color{blue}{5}\\
8\times \mathrm{OB}&=&4\sqrt{5}\times 5\\
\mathrm{OB}&=&\underline{\underline{ \frac{5\sqrt{5}}{2} }}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)
線分\(\,\mathrm{OG}\,\)も分かるので三平方の定理を利用しても良いです。
目的は\(\,\mathrm{OB}\,\)なので、
その必要がなかったと後で気がついても気にしなくて良いです。
方針が立ったら突っ走ってもたいして変わりません。
線分\(\,\mathrm{BO}\,\)を延長して相似を利用しても良いです。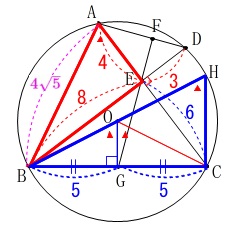
相似は分かり易いでしょう。
\(\begin{eqnarray}
\mathrm{AB:BE}&=&\mathrm{HB:BC}\\
4\sqrt{5}:8&=&\mathrm{HB}:10\\
8\times \mathrm{HB}&=&4\sqrt{5}\times 10\\
\mathrm{HB}&=&5\sqrt{5}
\end{eqnarray}\)
これは直径ですのでも求めるものを間違えないようにしましょう。
他にもいろいろと方針は立てられますがやめておきます。
以上です。
奈良県は年度によっての差はそれ程ないと言えます。
問題の構成から問われる計算量なども数年分見ておくとある程度見えてくるでしょう。
どこでも同じですが基礎をおろそかにして高得点はないとだけいっておきます。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
