2023年（令和5年度）京都府公立高校入試前期数学の問題と解説

2023年（令和5年度）京都府公立高校入試前期選抜の数学の問題と解説です。
レベルの高い偏りの少ない出題は全体的に例年通りです。
図形問題は折り返しの繰り返しなので相似合同の処理次第といえるでしょう。
恒例の規則性問題は文字式で処理できますが、
練習が足りていないと実際の試験の場では簡単に行くものではないです。

2023年（令和5年度）京都府公立入試前期選抜数学の問題

令和５年度京都府前【期選抜学力検査】「共通学力検査」問題です。

⇒　2023年（令和5年度）京都府公立入試前期選抜数学の問題ＰＤＦ

余白ページは省いてありますが、
利用しないと問題ごとの余白では足りないと思います。
（「計算力」より「作業」の比率が高いです。）

2023年（令和5年度）京都府公立入試前期選抜数学の解説

全国でも最難関の１つといえる公立入試なので心しておきましょう。
大問で６つあります。
恒例の規則性問題もありますので手を止めないように。

第１問小問集合

\(\,\large{1}\,\)
数値と文字式で処理できる計算問題達です。
(1)
　\(\hspace{10pt}-3^2\times \{7-(-4)^2\}\\
=-3^2\times (7-16)\\
=-9\times (-9)\\
=\underline{　81　}\)

計算順序と符号に注意です。
中かっこ（\(\{　\}\)）の中が先なので別に計算すると良いです。
(2)
　\(\hspace{10pt}\displaystyle \frac{3x-2y}{6}-\frac{4x-y)}{8}\\
\displaystyle =\frac{4(3x-2y)-3(4x-y)}{24}\\
\displaystyle =\frac{12x-8y-12x+3y}{24}\\
\displaystyle =\underline{\underline{　\frac{-5\,y}{24}　}}\)

通分して分子の計算に集中ですね。
答えは\(\,\displaystyle -\frac{5}{24}\,y\,\)でも同じです。
(3)
　\(\hspace{10pt}3\color{red}{\sqrt{50}}-\sqrt{2}-\color{blue}{\sqrt{54}}\div \sqrt{3}\\
=3\times \color{red}{5\times \sqrt{2}}-\sqrt{2}-\color{blue}{3\sqrt{6}}\div \sqrt{3}\\
=15\sqrt{2}-\sqrt{2}-3\sqrt{2}\\
=\underline{　11\sqrt{2}　}\)

素因数分解をしっかりやれば後は普通の計算順序です。
(4)
連立方程式は方針が決まっています。
　\( \begin{cases}
\hspace{4pt} 2x-3y=5　･･･①\\
\hspace{4pt} 3x-(4x-6y)=-1　･･･②
\end{cases}\)

一文字消去ですが、
第二方程式を処理しておきましょう。
　\(\begin{eqnarray}
3x-(4x-6y)&=&-1\\
-x+6y&=&-1　･･･②’
\end{eqnarray}\)
第一方程式の両辺を２倍して\(\,②’\,\)とで\(\,y\,\)を消去します。
　\(\hspace{20pt}4x-6y=10\\
\underline{+)\,-x+6y=-1　}\\
\hspace{24pt}3x\hspace{20pt}=9\\
\hspace{50pt}x=3\)
\(\,②’\,\)に戻して
　\(\begin{eqnarray}
-(3)+6\,y&=&-1\\
6\,y&=&2\\
y&=&\frac{1}{3}
\end{eqnarray}\)
答え\(\hspace{4pt}\displaystyle \underline{\underline{　x=3\,,\,y=\frac{1}{3}　}}\,\)

消去するのは\(\,x\,\)からでも良いし、戻す方程式もどれでも良いです。
(5)
変化の割合の問題なので各成分の増加量を見ます。
　\(\hspace{4pt}\displaystyle y=-2\,x^2\,\)
\(\,x\,\)座標が\(\,a\,\)から\(\,a+2\,\)まで変化するので
\(\hspace{10pt}(\,\color{blue}{a}\,,\,\color{red}{-2\,a^2}\,)\)
\(\hspace{10pt}(\,\color{blue}{a+2}\,,\,\color{red}{-2\,(\,a+2\,)^2}\,)\)
変化の割合が\(\,\color{magenta}{-40}\,\)であることから
　\(\begin{eqnarray}
(\,変化の割合\,)&=&\frac{　(\,y\,の増加量\,)　}{　(\,y\,の増加量\,)　}\\
\color{magenta}{-40}&=&\frac{\color{red}{-2\,(\,a+2\,)^2}-(\,\color{red}{-2\,a^2}\,)}{(\color{blue}{a+2})-\color{blue}{a}}\\
&=&\frac{-2a^2-8a-8+2a^2}{2}
\end{eqnarray}\)
分子の\(\,2a^2\,\)は消えます。
　\(\begin{eqnarray}
-4a-4&=&-40\\
-4a&=&-36\\
a&=&\underline{　9　}
\end{eqnarray}\)

これは計算量はどのくらいか知るために自分で計算した方が良いです。
他の問題も同様ですがこの程度の計算は毎年試されます。
(6)
展開は地道にやれば必ずできます。
ただ、計算に頼る問題は京都は出さないと思う。
　\(\hspace{10pt}(\color{red}{2x+y}+5)(\color{red}{2x+y}-5)\\
=\{(\color{red}{2x+y})+5\}\{(\color{red}{2x+y})-5\}\\
=(2x+y)^2-5^2\\
=\underline{　4x^2+4xy+y^2-25　}\)
※
共通部分が見えた人は２行目なくても良いです。

共通部分を文字でおいた方が分かり易いですね。
後は公式を利用して展開します。
　\((\color{red}{2x+y}+5)(\color{red}{2x+y}-5)\\
=(\mathrm{\color{red}{A}}+5)(\mathrm{\color{red}{A}}-5)\\
=\mathrm{A}^2-5^2\\
=(2x+y)^2-25\\
=4x^2+4xy+y^2-25\)
(7)
あからさまな解の公式です。
\(\hspace{10pt}6x^2+2x-1=0\)
ただし、答えまでの時間に差が出る係数ではあります。
　\(\begin{eqnarray}
x&=&\frac{-1\pm \sqrt{1^2-6\times (-1)}}{6}\\
&=&\frac{-1\pm \sqrt{1+6}}{6}\\
&=&\underline{\underline{　\frac{-1\pm \sqrt{7}}{6}　}}
\end{eqnarray}\)

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

この際だから１次の係数が偶数のときの解の公式も覚えておきましょう。
一応普通にやっておきます。
　\(\begin{eqnarray}
x&=&\frac{-2\pm \sqrt{2^2-4\cdot (6)\cdot (-1)}}{2\times 6}\\
&=&\frac{-2\pm \sqrt{4+24}}{12}\\
&=&\frac{-2\pm \sqrt{28}}{12}\\
&=&\frac{-2\pm 2\sqrt{7}}{12}\\
&=&\frac{-1\pm \sqrt{7}}{6}
\end{eqnarray}\)
※
ルートの中の「\(\,\cdot\,\)」は掛け算の意味です。
(8)
角度ですが正三角形と正五角形なので内角と外角が分かります。
（\(\,\color{red}{●}\,\)は正三角形の１角で60°です。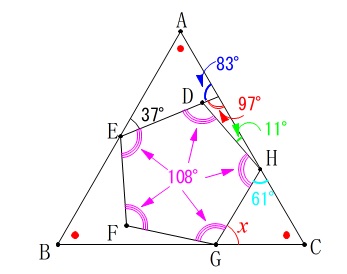）内角と三角形の内角の和から分かる角度を書き込んでおきました。
　\(\begin{eqnarray}
∠x+61°+60°&=&180°\\
∠x&=&180°-121°\\
&=&\underline{　59　}°
\end{eqnarray}\)

正五角形の外角の1つが\(\,72°\,\)であることから進めても同じです。
もちろん補助線もいろいろ引けると思います。
分かる角度を次々に書き込んで行くならどうでも良いです。
(9)
くじを引く順番関係なしにあたりくじを引く確率は同じなのですが、
３人目の「花子さんだけ」があたりくじを引く確率です。
\(\hspace{4pt}\color{red}{1}\,,\,\color{red}{2}\,,\,\color{blue}{3}\,,\,\color{blue}{4}\)
赤字の数字があたりだとしても同じなので樹形図で確認します。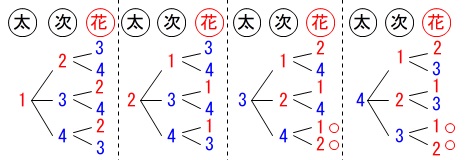３人続けて引く全通りは２４通り、
３番目の花子さんだけがあたりを引くのは４通り。
答え\(\hspace{4pt}\displaystyle \frac{4}{24}=\underline{\underline{　\frac{1}{6}　}}\)

太郎さんがはずれ、次郎さんがはずれたら後はあたりくじしか残りません。
一人目のはずれは４本中２本、
二人目は１本はずれが減って３本中１本がはずれだから
　\(\hspace{4pt}\displaystyle \frac{2}{4}\times \frac{1}{3}=\frac{1}{6}\)

くじを区別して樹形図で良いですよ。

第２問データと四分位範囲

\(\,\large{2}\,\)
データの扱いの基本通り小さい順に並べておけばなんとかなるでしょう。
生徒９人のデータは
\(\hspace{10pt}3\,,\,4\,,\,6\,,\,8\,,\,9\,,\,11\,,\,15\,,\,(\,a\,,\,b\,)\)
(1)
「すべて異なる」ことがポイントになります。
９人の平均値が\(\,\color{red}{8}\,\)であることから
　\(\begin{eqnarray}
\frac{56+a+b}{9}&=&\color{red}{8}\\
56+a+b&=&72\\
a+b&=&16　･･･①
\end{eqnarray}\)
\(\,0\,＜\,a\,＜\,b\,\)なので\(\,a\,\)の値から見ていくと、
\(\hspace{10pt}a=1\,,\,2\,,\,5\,,\,7\,\)
しかありません。
このうち\(\,b\,\)もすべてと異なる値で\(\,①\,\)を満たすのは
\(\hspace{10pt}\underline{　a=2\,,\,b=14　}\)

生徒９人のデータは
\(\hspace{10pt}2\,,\,3\,,\,4\,,\,6\,,\,8\,,\,9\,,\,11\,,\,14\,,\,15\,\)
(2)
先生のデータを加えて四分位範囲を９にします。
\(\hspace{10pt}2\,,\,3\,,\,4\,,\,6\,,\,8\,,\,9\,,\,11\,,\,14\,,\,15\,,\,\color{magenta}{●}\)

１０個のデータの四分位範囲は
\(\hspace{4pt}○○\color{red}{●}○○｜○○\color{blue}{●}○○\)
第３四分位数から第１四分位数を引きます。（\(\,\color{blue}{●}-\color{red}{●}\,\)）
右から３番目の値から左から３番目の値を引いて９ということです。

おおよその目安をつけることもできますが順に見ていくと
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,6\,,\,8\,,\,9\,,\,11\,,\,\color{blue}{14}\,,\,15\,,\,\color{magenta}{●}\)
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,6\,,\,8\,,\,9\,,\,11\,,\,\color{blue}{14}\,,\,\color{magenta}{●}\,,\,15\)
このとき四分位範囲は10。×
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,6\,,\,8\,,\,9\,,\,11\,,\,\color{blue}{●}\,,\,14\,,\,15\)
このとき
　\(\begin{eqnarray}
\color{blue}{●}-4&=&9\\
\color{blue}{●}&=&13
\end{eqnarray}\)
答え\(\hspace{4pt}\underline{　13　}\)

続きを見てくと
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,6\,,\,8\,,\,9\,,\,\color{magenta}{●}\,,\,\color{blue}{11}\,,\,14\,,\,15\)
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,6\,,\,8\,,\,\color{magenta}{●}\,,\,9\,,\,\color{blue}{11}\,,\,14\,,\,15\)
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,6\,,\,\color{magenta}{●}\,,\,8\,,\,9\,,\,\color{blue}{11}\,,\,14\,,\,15\)
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{4}\,,\,\color{magenta}{●}\,,\,6\,,\,8\,,\,9\,,\,\color{blue}{11}\,,\,14\,,\,15\)
\(\hspace{4pt}2\,,\,3\,,\,\color{red}{●}\,,\,4\,,\,6\,,\,8\,,\,9\,,\,\color{blue}{11}\,,\,14\,,\,15\)
\(\hspace{4pt}2\,,\,\color{magenta}{●}\,,\,\color{red}{3}\,,\,4\,,\,6\,,\,8\,,\,9\,,\,\color{blue}{11}\,,\,14\,,\,15\)
\(\hspace{4pt}\color{magenta}{●}\,,\,2\,,\,\color{red}{3}\,,\,4\,,\,6\,,\,8\,,\,9\,,\,\color{blue}{11}\,,\,14\,,\,15\)
四分位範囲が９になることはありません。
（先生の位置を決めたら引き算するだけなので大した計算ではありません。）

第３問立体問題（正八面体）

\(\,\large{3}\,\)
正八面体の問題です。
正八面体は元が立方体なので利用すれば長さや体積計算はややこしくはありませんが、
高さを求める(3)は立体を転がすことができるかどうかです。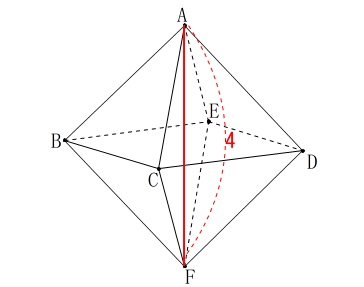正八面体はすべての面が正三角形なので、
四角形\(\,\mathrm{BCDE}\,\)と\(\,\mathrm{ACFE}\,\)が正方形になります。
（ひし形だと各面が正三角形にならない。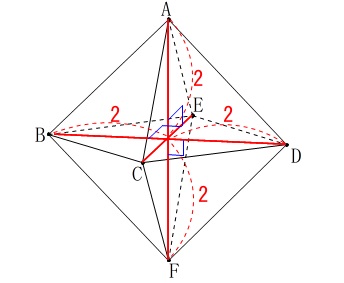）(1)
正八面体の１辺は直角二等辺三角形の斜辺になるので
\(\hspace{10pt}\underline{　2\sqrt{2}　}\,(\,\mathrm{cm}\,)\)
(2)
正方形の対角線の交点が\(\,\mathrm{H}\,\)です。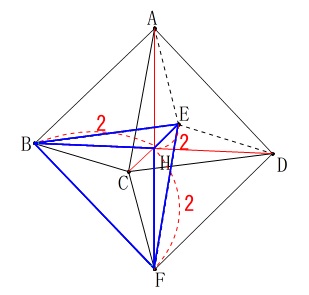三角錐の体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times \mathrm{\color{red}{△BHE}}\times \mathrm{\color{blue}{HF}}\\
&=&\frac{1}{3}\times \color{red}{\frac{1}{2}\times 2\times 2}\times \color{blue}{2}\\
&=&\underline{\underline{　\frac{4}{3}　}}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

これは正八面体の体積の\(\,\displaystyle \frac{1}{8}\,\)です。
(3)
これは色々考えられますが、(2)を誘導と見ます。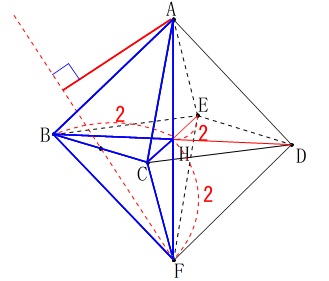底面を\(\,\mathrm{△BFC}\,\)として点\(\,\mathrm{A}\,\)からの距離\(\,\color{red}{h}\,\)を高さとする立体は、
三角錐\(\,\mathrm{ABCH}\,\)と三角錐\(\,\mathrm{FBCH}\,\)の和です。
（(2)で求めた体積２つ分です。）正三角形\(\,\mathrm{BFC}\,\)の面積は（三平方の定理から高さを出して）
　\(\begin{eqnarray}
\mathrm{△BFC}&=&\frac{1}{2}\times 2\sqrt{2}\times \sqrt{6}\\
&=&\color{blue}{2\sqrt{3}}
\end{eqnarray}\)
よって求める点\(\,\mathrm{A}\,\)と平面\(\,\mathrm{BFC}\,\)との距離\(\,\color{red}{h}\,\)は
　\(\begin{eqnarray}
\frac{1}{3}\times \mathrm{△BCF}\times \color{red}{h}&=&\frac{4}{3}\times 2\\
\frac{1}{3}\times \color{blue}{2\sqrt{3}}\times \color{red}{h}&=&\frac{8}{3}\\
\color{red}{h}&=&\frac{8}{2\sqrt{3}}\\
&=&\underline{\underline{　\frac{4\sqrt{3}}{3}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

転がしても体積は変わらないので見方を変えただけです。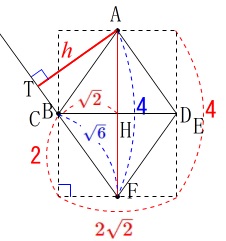\(\,\mathrm{B\,,\,C}\,\)が重なる方向から見ると平面で考えられます。
点\(\,\mathrm{A}\,\)から面\(\,\mathrm{BFC}\,\)に下ろした垂線\(\,\mathrm{AT}\,\)は、
線分\(\,\mathrm{BC}\,\)の中点と直線\(\,\mathrm{AF}\,\)を含む平面上にあります。
\(\hspace{10pt}\mathrm{△FHB}\,\)∽\(\,\mathrm{△FTA}\,\)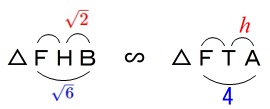　\(\begin{eqnarray}
\mathrm{HB:FB}&=&\mathrm{TA:FA}\\
\color{red}{\sqrt{2}}:\color{blue}{\sqrt{6}}&=&\color{red}{h}:\color{blue}{4}\\
\sqrt{6}\times h&=&4\times \sqrt{2}\\
h&=&\frac{4\sqrt{2}}{\sqrt{6}}\\
&=&\frac{4\sqrt{12}}{6}\\
&=&\underline{\underline{　\frac{4\sqrt{3}}{3}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

(2)を考えれば立体を転がす方が自然な流れですかね。
ちなみにですが、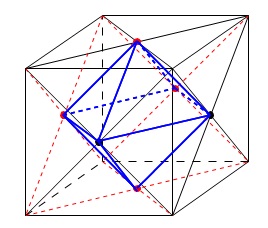正八面体は立方体から作られます。

第４問関数（反比例）と面積

\(\,\large{4}\,\)
関数ですが軽めです。
\(\hspace{10pt}\displaystyle y=\frac{a}{x}\)
\(\hspace{10pt}\mathrm{A}\,(\,2\,,\,6\,)\)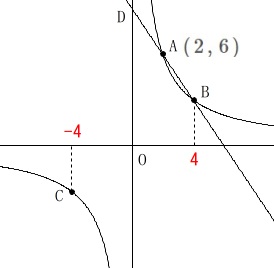(1)
比例定数を決めて、面積を求めます。
反比例の関数は点\(\,\mathrm{A}\,\)を通るので
　\(\begin{eqnarray}
6&=&\frac{a}{2}\\
a&=&\underline{　12　}
\end{eqnarray}\)

関数は\(\,\displaystyle y=\frac{12}{x}\)

点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,4\,\)なので\(\,\mathrm{B}\,(\,4\,,\,3\,)\)
点\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,-4\,\)なので\(\,\mathrm{C}\,(\,-4\,\,-3\,)\)
また、２点\(\,\mathrm{A\,,\,B}\,\)を通る直線は
\(\hspace{10pt}\displaystyle y=-\frac{3}{2}\,x+9\)
なので点\(\,\mathrm{D}\,\)は\(\,\mathrm{D}\,(\,0\,,\,9\,)\,\)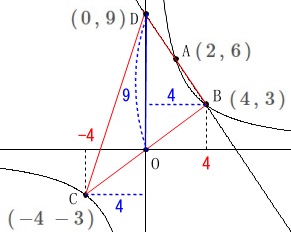求める面積は２つの三角形の和になります。
　\(\begin{eqnarray}
\mathrm{△BDC}&=&\mathrm{△ODB+△ODC}\\
&=&\frac{1}{2}\times 9\times 4+\frac{1}{2}\times 9\times 4\\
&=&\underline{　36　}
\end{eqnarray}\)

たまたま底辺と高さが同じだから片方を２倍すれば良いですが、
三角形の面積計算で足しておきました。

等積移動させればもっときれいに計算できるけど必要ありません。
(2)
点\(\,\mathrm{B}\,\)を通り\(\,x\,\)軸に平行な直線を引きます。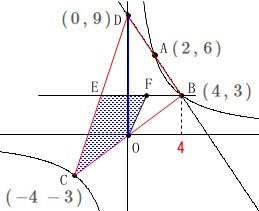四角形\(\,\mathrm{COFE}\,\)の面積が\(\,\mathrm{△BDC}\,\)の\(\displaystyle \,\frac{2}{5}\,\)になるときです。

ただ、点\(\,\mathrm{E}\,\)は２点\(\,\mathrm{C\,,\,D}\,\)の中点で、
\(\hspace{10pt}\mathrm{E}\,(\,-2\,,\,3\,)\)
（直線\(\,\mathrm{DC}\,\)上の点で\(\,y\,\)座標が\(\,\mathrm{B}\,\)と同じ\(\,3\,\)としても良いです。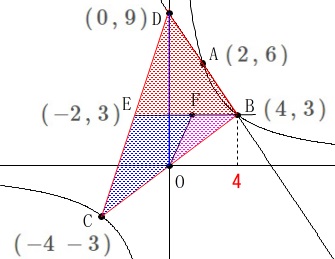）底辺がはっきりしてくるので残りの三角形２つの面積の和が、
\(\,\mathrm{△BDC}\,\)の面積の\(\displaystyle \,\color{red}{\frac{3}{5}}\,\)のなるときを考えます。

点\(\,\mathrm{F}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると\(\,\mathrm{F}\,(\,t\,,\,3\,)\,\)と表せて、
\(\,\mathrm{△OFB}\,\)は底辺\(\hspace{10pt}\mathrm{FB}=\color{red}{4-t}\,\)、
高さ\(\,\color{blue}{3}\,\)の三角形なので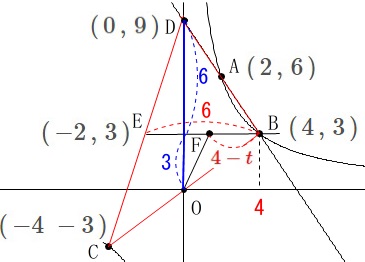　\(\begin{eqnarray}
\mathrm{△BDC}\times \color{red}{\frac{3}{5}}&=&\mathrm{△DEB+△OBF}\\
36\times \frac{3}{5}&=&\frac{1}{2}\times 6\times 6+\frac{1}{2}\times (4-t)\times 3\\
\frac{108}{5}&=&24-\frac{3}{2}\,t\\
t&=&\underline{\underline{　\frac{8}{5}　}}
\end{eqnarray}\)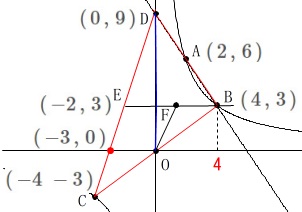
四角形\(\,\mathrm{COFE}\,\)の面積で進めるのも、
直線\(\,\mathrm{DC}\,\)と\(\,x\,\)軸との交点が\(\,(\,-3\,,\,0\,)\,\)なので大した計算にはなりません。
（自分でやってみて下さい。）

第５問平面図形（折り返しと相似）

\(\,\large{5}\,\)
折り返しに折り返して、相似だらけなので補助線なしでいきます。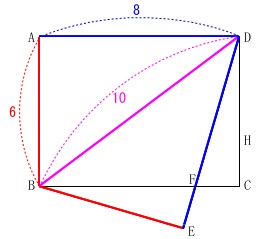一回目の折り返しで分かる長さを示しておきます。
三平方の定理から\(\,\mathrm{BD}\,\)の長さは出しておきましょう。
角度も示すと合同も含めた相似が見てきますよ。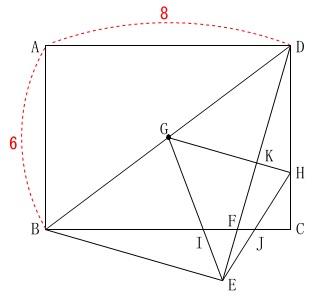二回目の折り返しで一気に相似が増えますので、
説明で使うと思われる交点の記号を増やしてあります。問題に沿って説明しても良いですが折り返しなので、
辺や角度が等しいところが多いのである程度図示しておきます。

点\(\,\mathrm{G}\,\)が線分\(\,\mathrm{BD}\,\)の中点になるのは、
直線\(\,\mathrm{GK}\,\)が折り返しの軸になるので中点連結定理からです。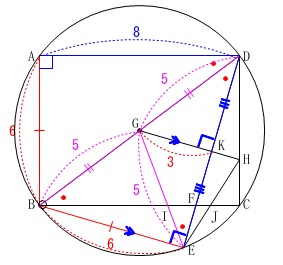直径\(\,\mathrm{BD}\,\)の円をイメージして、
弦\(\,\mathrm{DE}\,\)の垂直二等分線が交わっているから点\(\,\mathrm{G}\,\)が中心としても良いです。

ここまででだいたいのことは分かるのですが、
後は問題に応じて見ておきましょう。
(1)
相似の証明です。
\(\hspace{10pt}\mathrm{△IGB}\,\)∽\(\,\mathrm{△IFE}\,\)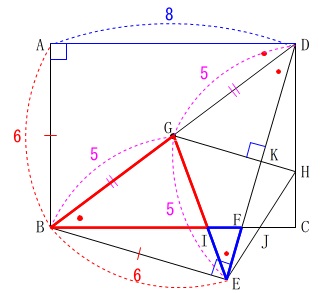図の中で証明は終わっています。
折り返しているので右上２つの\(\,\color{red}{●}\,\)の角は等しく、
長方形なので錯角が等しく右上の\(\,\color{red}{●}\,\)と左下の\(\,\color{red}{●}\,\)が等しくなります。
二回目の折り返しで\(\,\mathrm{△GED}\,\)が二等辺三角形になるので、
底角が等しいことから
\(\hspace{10pt}\mathrm{∠GBI=∠FEI}　･･･①\)
対頂角が等しいことから
\(\hspace{10pt}\mathrm{∠BIG=∠EIF}　･･･②\)
なので
「２組の角がそれぞれ等しい。」
の相似条件がそろいます。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明の書き方にはある程度決まりはあります。
ただし、ルールを守っていれば条件をそろえる順序や書き方は自由です。
自分で書きやすい方法で良いけど、先ずは「真似る」方法で良いですよ。
(2)
これは合同から三平方の定理のお決まり問題です。
線分\(\,\mathrm{\color{magenta}{EF}}\,\)を\(\,\color{magenta}{x}\,\)とすると、
\(\hspace{10pt}\mathrm{\color{blue}{DF}}=\mathrm{DE-EF}=\color{blue}{8-x}\)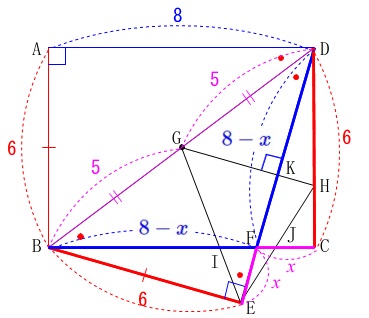合同だからどちらでも良いですが、
\(\,\mathrm{△BEF}\,\)か\(\,\mathrm{△DCE}\,\)に三平方定理を利用して
　\(\begin{eqnarray}
x^2+6^2&=&(8-x)^2\\
x^2+36&=&x^2-16x+64\\
36&=&-16x+64\\
16x&=&64-36\\
x&=&\frac{28}{16}=\underline{\underline{　\frac{7}{4}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

これで(1)の相似の比が求まりました。
\(\hspace{10pt}\displaystyle \mathrm{GB:FE}=\color{magenta}{5}:\color{magenta}{\frac{7}{4}}=20:7\)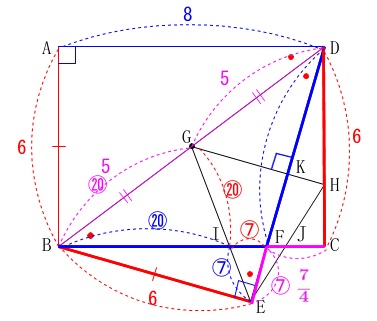(3)
線分\(\,\mathrm{BI}\,\)の長さを求めますが、
ここは誘導にきっちり乗って(1)(2)を利用しましょう。

分かる長さを１つだけ追加しておきましょう。
\(\hspace{10pt}\displaystyle \mathrm{\color{blue}{BF}=\color{blue}{DF}}=\color{blue}{8}-\color{magenta}{\frac{7}{4}}=\color{blue}{\frac{25}{4}}\)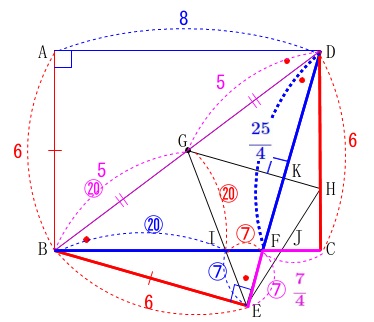後は長さを求めるだけですが、
分数の文字をいろいろあつかうのはメンドウなので、
相似比から
\(\hspace{10pt}\mathrm{\color{blue}{BI}}=\color{blue}{20\,a}\,,\,\mathrm{\color{blue}{EI}}=\color{blue}{7\,a}\)
とすると
\(\hspace{10pt}\displaystyle \mathrm{\color{red}{IF}}=\color{red}{\frac{25}{4}-20\,a}\,,\,\mathrm{\color{red}{IG}}=\color{red}{5-7\,a}\)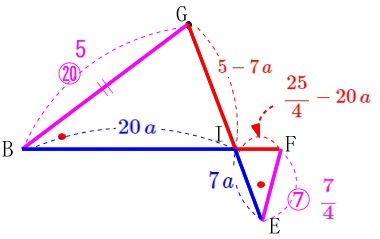相似比から
　\(\begin{eqnarray}\displaystyle
(\,5-7\,a):\left(\,\frac{25}{4}-20\,a\,\right)&=&20:7\\
20\times \left(\,\frac{25}{4}-20\,a\,\right)&=&7\times (\,5-7\,a)\\
125-400\,a&=&35-49\,a\\
-351\,a&=&-90\\
a&=&\frac{90}{351}=\frac{10}{39}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}
\mathrm{\color{blue}{BI}}&=&\color{blue}{20\,a}\\
&=&20\times \frac{10}{39}\\
&=&\underline{\underline{　\frac{200}{39}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

線分\(\,\mathrm{IF}\,\)を相似比から表すと
　\(\begin{eqnarray}\displaystyle
\mathrm{IG:IF}&=&7:4\\
(5-7\,a):\mathrm{IF}&=&20:7\\
20\times \mathrm{IF}&=&7\times (5-7\,a)\\
\mathrm{IF}&=&\color{blue}{\frac{7(\,5-7\,a\,)}{20}}
\end{eqnarray}\)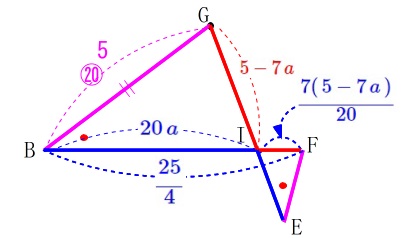線分\(\,\mathrm{BF}\,\)の長さから
　\(\begin{eqnarray}
\mathrm{BI+IF}&=&\mathrm{BF}\\
20\,a+\frac{7(\,5-7\,a\,)}{20}&=&\frac{25}{4}\\
400\,a+7(\,5-7a\,)&=&5\times 25\\
400\,a+35-49\,a&=&125\\
351\,a&=&90\\
a&=&\frac{10}{39}
\end{eqnarray}\)
よって、
\(\hspace{10pt}\displaystyle \mathrm{BI}=\color{blue}{20a}=\underline{\underline{　\frac{200}{39}　}}(\,\mathrm{cm}\,)\)

求める\(\,\mathrm{BI}\,\)を\(\,\color{blue}{20\,a}\,\)とおいているので、
最後にミスをしなければどっちでも良いです。
※
もちろん他にも相似はたくさんあるので方針は違っても良いです。

第６問規則性問題

\(\,\large{6}\,\)
京都と言えば、ですよね。
規則性の問題ですがいろいろな見方ができるので簡単に解説しておきます。
(1)
先ずは規則性を見ていく意味で数えましょうか。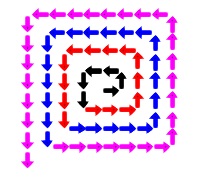数値ボックスに入れた数字で見ていきます。
\(\,1\,\)を入れたとき黒\(\,→\,\)で\(\,6\,\)です。
\(\,2\,\)を入れたとき赤\(\,\color{red}{→}\,\)が加わり\(\,20\,\)です。
\(\,3\,\)を入れたとき青\(\,\color{blue}{→}\,\)が加わり\(\,42\,\)です。
\(\,4\,\)を入れたとき桃\(\,\color{magenta}{→}\,\)が加わり\(\,72\,\)です。
答え　\(\,\underline{　72　}\,\)

ここまでは根性出して確実に取っておきたいですね。

足し算なのでどうやって増えていくかを見ておきましょう。
数値ボックスに
\(\,1\,\)を入れたとき
\(\hspace{10pt}1\times 2+2\times 2=6\)
（右と上は同じ、左と下は同じ数\(\,→\,\)があります。）
\(\,2\,\)を入れたとき（\(\,(\color{red}{3}\times 2+\color{red}{4}\times 2)\,\)増えるので）
\(\hspace{10pt}6+(\color{red}{6}+\color{red}{8})=20\)
\(\,3\,\)を入れたとき（\(\,(\color{blue}{5}\times 2+\color{blue}{6}\times 2)\,\)増えるので）
\(\hspace{10pt}20+(\color{blue}{10}+\color{blue}{12})=42\)
\(\,4\,\)を入れたとき（\(\,(\color{magenta}{7}\times 2+\color{magenta}{8}\times 2)\,\)増えるので）
\(\hspace{10pt}42+(\color{magenta}{14}+\color{magenta}{16})=72\)

これって偶数の和だというのは分かりますが、
文字式で表すにはどうすれば良いか？わかりにくいですよね。

１つの見方ですが矢印の終点を点で表してみます。
（同じように矢印を動かしても良いです。）最後の左下の点を移動させてまん中の空いたところを埋めると、長方形になります。
\(\,1\,\)のとき（黒だけのとき）
\(\hspace{10pt}2\times 3=6\)
\(\,2\,\)のとき（赤が増えたとき）
\(\hspace{10pt}4\times 5=20\)
\(\,3\,\)のとき（青が増えたとき）
\(\hspace{10pt}6\times 7=42\)
ボックスに入れる数値の２倍とそれより１大きい数の積です。
\(\hspace{10pt}2n(2n+1)\)
これは全体の矢印の数です。
問題は上下左右に分かれて見るので、
点で見ると後が続けづらいと思うので矢印に戻しておきます。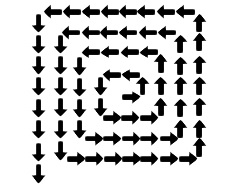(2)
左矢印\(\,\color{red}{←}\,\)の数です。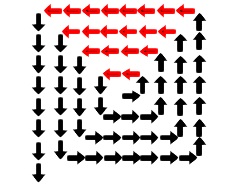これは\(\,20\,\)個の偶数の和ですね。
　\(\hspace{10pt}\color{red}{2}+\color{blue}{4}+6+8+\cdots +\color{blue}{38}+\color{red}{40}\\
=(\color{red}{2}+\color{red}{40})+(\color{blue}{4}+\color{blue}{38})+\cdots +(20+22)\\
=42\times \color{magenta}{10}\\
=\underline{　420　}\)

初めの数と最後の数からそれぞれ順に足していくと、
増えていく数と減っていく数の和になるので同じで、
和の組が\(\,\color{magenta}{10}\,\)組になるので計算は楽です。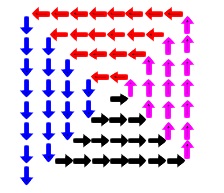右と上、左と下は同じ数なので、
合計の数から別の計算もできますが、、、やっておきます。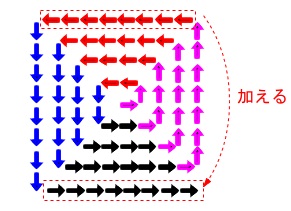左向きの\(\,\color{red}{←}\,\)の最上段分\(\,\color{red}{40}\,\)を一番下に加えて、
同じ偶数で分割するようにすると\(\,4\,\)分割できるので、
元の全体の個数\(\,40\times 41\,\)から
　\(\hspace{10pt}\displaystyle \frac{40(40+1)+\color{red}{40}}{4}\\
\displaystyle =\frac{1680}{4}=\underline{　420　}\)

規則性の問題はいろいろ方針があるということで、
出題者の意図は考えずに進めて行きます。
で、(3)でそぞれぞれの方向を聞かれたところで、
そろそろどう考えたか種明かししておきます。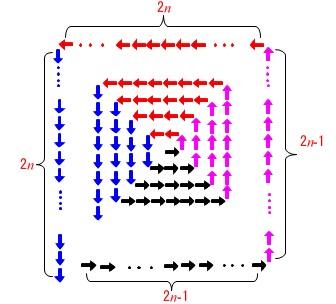奇数の和と偶数の和に分けることができます。
右\(\,→\,\)と上\(\,\color{magenta}{↑}\,\)の和はそれぞれ奇数の和なので、
数値ボックスに入れる数を\(\,n\,\)とすると、
右矢印の数の和\(\,N_{(\rightarrow )}\,\)と上矢印の数の和\(\,N_{(\color{magenta}{\uparrow} )}\,\)は
\(\hspace{10pt}N_{(\rightarrow )}=N_{(\color{magenta}{\uparrow} )}=\displaystyle n^2\)
左\(\,\color{red}{←}\,\)と下\(\,\color{blue}{↓}\,\)の和はそれぞれ偶数の和なので
左矢印の数の和\(\,N_{(\color{red}{\leftarrow} )}\,\)と下矢印の数の和\(\,N_{(\color{blue}{\downarrow} )}\,\)は
\(\hspace{10pt}\displaystyle N_{(\color{red}{\leftarrow} )}=N_{(\color{blue}{\downarrow} )}=n^2+n=\,n\,(\,n+1\,)\)

一応説明しておくと\(\,1\,\)から\(\,n\,\)までの奇数の和は、
平方数になっているので推測もできるでしょう。
\(\hspace{10pt}1\,,\,4\,,\,9\,,\,16\,,\,\cdots \,,\,n^2\)
ギリシャ時代の証明では図形的に説明できます。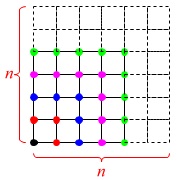奇数を順に並べていくと平方数になることが分かります。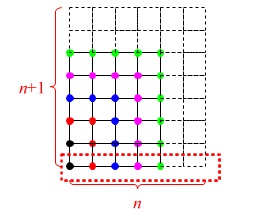偶数の和は奇数に１つずつ足した和になるので、
奇数の和に\(\,n\,\)加えることになります。

部分的な個数が分かったので全体の矢印の和が、
先ほどの数と一致していることを確認しておいて下さい。
\(\hspace{10pt}2\times n(n+1)+2\times n^2\\
=2n^2+2n+2n^2\\
=4n^2+2n\\
=2n(2n+1)\)
(3)
上、左、下矢印の和と右矢印の差が\(\,6160\,\)です。
数値ボックスに入力した自然数を\(\,n\,\)とすると
　\(\begin{eqnarray}\displaystyle
N_{(\color{magenta}{\uparrow} )}+N_{(\color{red}{\leftarrow} )}+N_{(\color{blue}{\downarrow} )}-N_{(\rightarrow )}&=&6160\\
n(n+1)+n(n+1)+n^2-n^2&=&6160\\
2n^2+2n-6160&=&0\\
n^2+n-3080&=&0\\
(n-55)(n+56)&=&0\\
n&=&55\,,\,-56
\end{eqnarray}\)
自然数なので\(\,n=55\,\)です。

答え\(\,\underline{　55　}\,\)

全体の数から右矢印を引いた部分が、
上、左、下矢印の合計なので
\(\hspace{10pt}2n(2n+1)-n^2\)
さらに右矢印との差が\(\,6160\,\)なので
　\(\begin{eqnarray}\displaystyle
\{2n(2n+1)-n^2\}-n^2&=&6160\\
4n^2+2n-2n^2&=&6160\\
2n^2+2n-6160&=&0\\
n^2+n-3080&=&0\\
(n-55)(n+56)&=&0
\end{eqnarray}\)
でも良いですよ。

因数分解をするとき\(\,3080\,\)を素因数分解して、
\(\hspace{10pt}3080=\color{red}{2^3}\times \color{blue}{5}\times \color{red}{7}\times \color{blue}{11}\)
\(\,n\,\)の係数が\(\,1\,\)だから近い数字の積になるので、
\(\hspace{4pt}50\times 50=\,2500\,,\,60\times 60=\,3600\)
であることから\(\,50\,\)から\(\,60\,\)までの因数に分けることを考えれば早いです。

他にも規則性を見ていくことはできると思います。
何でも良いですが、ある程度文字式に慣れておくと良いですね。
※
京都府の規則性はそれ程単純でないときもあります。
徹底した作業でしか答えは出ないほど厳しい、と覚悟しておくと良いです。

別解などを加えていませんので解説が不足しているかもしれませんが以上です。
見直ししませんので入力ミスなどありましたらご指摘下さい。

⇒　京都府公立高校入試数学の過去問と解答解説

公立入試としては最高峰といって良い難易度です。
ただし、基本をしっかりおさえているかを見ている応用だということは理解しておきましょう。