2023年（令和5年度）大阪府公立高校入試数学Ｂ問題の解説

２０２３年（令和５年度）大阪府公立高校入試の数学Ｂ問題と解説です。
例年通りＢ問題は標準的で出題分野に偏りはありません。
質問がシンプルな問題がそろっているので取り組みやすいとは思いますが、
手を止めないようにしっかり作業はしないと基礎も活かせません。

2023年（令和5年度）大阪府公立高校入試数学Ｂの問題

大阪府立高校入試令和５年度のＢ問題です。

⇒　令和5年度大阪府公立高校入試数学Ｂの問題ＰＤＦ

解答用紙も含めた大阪府公開分も載せておきます。

⇒　令和5年度大阪府公立高校入試数学Ｂの問題公開分ＰＤＦ

印刷の大きさによっては空白が小さくなるのでお好きな方を利用して下さい。
試験感覚に慣れておきたい場合は作業しやすい上のＰＤＦを利用すると良いです。

2023年（令和5年度）大阪府公立高校入試数学Ｂ問題の解説

Ａ問題は基礎の確認として済ませてあるとして、
Ｂ問題の解説は簡単に済ませます。
問題は大問で４つあります。
問題数は多くはありませんが全体を通して作業のボリュームは軽めとは言えません。

第１問計算小問集合

\(\,\large{1}\,\)
計算が５つあります。
(1)
　\(\hspace{10pt}2\times (-3)-4^2\\
=-6-16\\
=\underline{　-22　}\)

符号と演算の記号の区別ができていれば問題ありません。
(2)
　\(\hspace{10pt}5(2a+b)-4(a+3b)\\
=10a+5b-4a-12b\\
=\underline{　6a-7b　}\)

１行目から２行目の展開は暗算しない方が早いしミスが減ります。
(3)
　\(\hspace{10pt}2a\times 9ab\color{red}{\div 6a^2}\\
\displaystyle =\frac{2a\times 9ab}{\color{red}{6a^2}}\\
=\underline{　3\,b　}\)

文字式でも掛け算割り算の混合計算は分数処理で『約分』です。
(4)
　\(\hspace{10pt}(x+1)^2+x(x-2)\\
=x^2\color{red}{+2x}+1+x^2\color{red}{-2x}\\
=\underline{　2\,x^2+1　}\)

展開して同類項をまとめるだけです。
(5)
　\(\hspace{10pt}(2\sqrt{5}+\sqrt{3})(2\sqrt{5}-\sqrt{3})\\
=20-3\\
=\underline{　17　}\)

展開公式を利用しただけですが、
暗算が過ぎるとミスの原因になります。
\(\hspace{10pt}\color{red}{(a+b)(a-b)=a^2-b^2}\)

第２問文字式から関数および図形問題までの小問集合

\(\,\large{2}\,\)
小問が８つ並びますが関係は続かないので切れ換えをしっかり。
(1)
代入する場合の注意点は意識しておきましょう。
\(\hspace{10pt}\color{red}{a}=\color{red}{-6}\,,\,\color{blue}{b}=\color{blue}{5}\)
　\(\hspace{10pt}\color{red}{a}^2-8\color{blue}{b}\\
=(\color{red}{-6})^2-8\times (\color{blue}{5})\\
=36-40\\
=\underline{　-4　}\)

与式を変形はしなくて良いですが、
正の数でも負の数でも（かっこ）をつけて代入です。
(2)
２次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
x^2-11x+18&=&0\\
(x-2)(x-9)&=&0\\
x&=&\underline{　2\,,\,9　}
\end{eqnarray}\)

解の公式でも良いですが、
定数項１８に着目して左辺の因数分解から、ですね。
※
方程式を解くことと、解を求めることは同じことです。
(3)
差が自然数になるので\(\,n\,\)は\(\,78\,\)の約数です。
\(\hspace{10pt}\displaystyle \color{red}{5}-\frac{78}{n}\)

約数を書き出すと
\(\hspace{4pt}1\,,\,2\,,\,3\,,\,6\,,\,13\,,\,26\,,\,39\,,\,78\)
このうち差が自然数になるのは引く数が\(\,\color{red}{5}\,\)より小さい場合で、
\(\hspace{10pt}n=26\,,\,39\,,\,78\)
最も小さな\(\,n\,\)は\(\,26\,\)です。
※
約数は\(\,1\times 78\,,\,2\times 39\,,\,3\times 26\,,\,6\times 13\)
のように対になる数を探すと早いです。

答え\(\hspace{10pt}n=\underline{　26　}\)

約数の探し方ですが素因数分解でして
\(\hspace{10pt}78=2\times 3\times 13\)
これから８つの約数を書き出しても良いです。
(4)
変化の割合は
\(\hspace{10pt}\displaystyle (\,変化の割合\,)=\frac{　(\,\color{red}{y\,の増加量}\,)　}{　(\,\color{blue}{x\,の増加量}\,)　}\)

関数\(\,\displaystyle y=\frac{10}{x}\,\)において
\(\hspace{10pt}(\,\color{blue}{1}\,,\,\color{red}{10}\,)\)
\(\hspace{10pt}(\,\color{blue}{5}\,,\,\color{red}{2}\,)\)
なので
\(\hspace{10pt}\displaystyle (\,変化の割合\,)=\frac{　\color{red}{2}-\color{red}{10}　}{　\color{blue}{5}-\color{blue}{1}　}=\underline{　-2　}\)

増加量を求めるとき引く方向を間違えないように注意しましょう。
(5)
確率です。
樹形図を書いて終わりですが、
全部で１５通りだということは確認しておきましょう。

箱Ａから取り出す数字\(\,\color{red}{a}\,：\color{red}{1}\,,\,\color{red}{2}\,,\,\color{red}{3}\)
箱Bから取り出す数字\(\,\color{blue}{b}\,：\color{blue}{1}\,,\,\color{blue}{3}\,,\,\color{blue}{5}\,,\,\color{blue}{7}\,,\,\color{blue}{9}\)
において、
\(\hspace{10pt}\displaystyle 1\,＜\,\frac{\color{blue}{b}}{\color{red}{a}}\,＜\,4\)
となるのは\(\,\color{red}{a}\,\)（少ない）で場合分けして調べると
\(\hspace{4pt}\,\color{red}{1}\,－\,\color{blue}{3}\,\)
\(\hspace{4pt}\,\color{red}{2}\,－\,\color{blue}{3}\,,\,\color{blue}{5}\,,\,\color{blue}{7}\,\)
\(\hspace{4pt}\,\color{red}{3}\,－\,\color{blue}{5}\,,\,\color{blue}{7}\,,\,\color{blue}{9}\,\)
の７通りです。

答え\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{7}{15}　}}\)

樹形図の方が分かり易く早いです。
(6)
箱ひげ図の読み取りです。
すべて選ぶので一つひとつ見ていきます。
ア
剣道部と卓球部は最大値が\(\,60\,\)以上なので少なくても\(\,2\,\)人はいます。×
イ
四分位範囲は箱の幅なのでどちらも同じ\(\,5\,\)回です。○
ウ
範囲は最大値から最小値までの幅なので剣道部が最も大きい。×
エ
第１四分位数は箱の左端なので最も小さいのは剣道部です。×
オ
剣道部の中央値は５５回よりも大きいので半数以上は５５回以上。○

答え\(\hspace{4pt}\underline{　イ\,,\,オ　}\)

剣道部の中央値（第２四分位数）は５５より大きいので、
人数が奇数の場合中央値となる人を含めて「半数より」大きく、
偶数の場合少なくとも「半数以上」になります。
(7)
表面積から高さを求めます。
展開図を書いて表面積を\(\,a\,\)を使って表せば簡単な方程式です。
※長さの単位は\(\,\mathrm{cm}\,\)です。

半径が\(\,\color{red}{4}\,\)だから
底面積：\(\hspace{4pt}\color{blue}{16\,\pi}\)
側面の横の長さは底面の円周\(\,\color{red}{8\,\pi}\,\)だから
側面積：\(\hspace{4pt}\color{magenta}{8\,a\,\pi}\)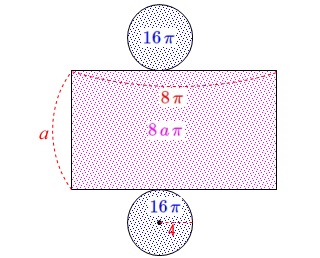この表面積が\(\,120\,\pi\,\)なので
　\(\begin{eqnarray}
2\times \color{blue}{16\,\pi}+\color{magenta}{8\,a\,\pi}&=&120\,\pi\\
32\,\pi+8\,a\,\pi&=&120\,\pi\\
8\,a\,\pi&=&88\,\pi\\
a&=&\underline{　11　}\mathrm{cm}
\end{eqnarray}\)

部分的な面積は分かり易いので展開図を書いて確認しながら進めると楽です。
(8)
普通に関数問題なので座標を分かるだけ書き出します。
放物線は\(\hspace{4pt}y=a\,x^2\,\)、
直線\(\,\ell\,\)は\(\hspace{4pt} \displaystyle y=\frac{1}{3}\,x-1\,\)です。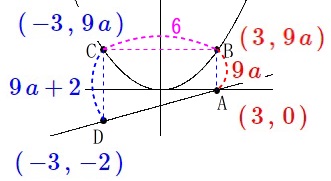
点\(\,\mathrm{A}\,\)は\(\,\ell\,\)と\(\,x\,\)軸（\(\,y=0\,\)）との交点なので
　\(\begin{eqnarray}
\frac{1}{3}x-1&=&0\\
x&=&3
\end{eqnarray}\)
から\(\,\mathrm{A}\,\color{red}{(\,3\,,\,0\,)}\,\)で、
点\(\,\mathrm{B}\,\)は点\(\,\mathrm{A}\,\)と\(\,x\,\)座標が同じなので、
\(\hspace{4pt}\mathrm{B}\,\color{red}{(\,3\,,\,9\,a\,)}\)
点\(\,\mathrm{C}\,\)は\(\,y\,\)軸で点\(\,\mathrm{B}\,\)と対称な点となるので\(\,y\,\)座標は同じで
\(\hspace{4pt}\mathrm{C}\,\color{blue}{(\,-3\,,\,9\,a\,)}\)
点\(\,\mathrm{D}\,\)は点\(\,\mathrm{C}\,\)と\(\,x\,\)座標が同じ\(\,\ell\,\)上の点なので
\(\hspace{4pt}\mathrm{D}\,\color{blue}{(\,-3\,,\,-2\,)}\)
四角形\(\,\mathrm{ABCD}\,\)は台形で、
上底と下底はそれぞれ
\(\hspace{4pt}\mathrm{AB}=\color{red}{9\,a}\,,\,\mathrm{DC}=\color{blue}{9\,a+2}\)
高さは\(\,\mathrm{BC}=\color{magenta}{6}\,\)となるので面積が\(\,21\,\)だから
　\(\begin{eqnarray}
\frac{(\color{red}{9\,a})+(\color{blue}{9\,a+}2)}{2}\times \color{magenta}{6}&=&21\\
18\,a+2&=&7\\
18\,a&=&5\\
a&=&\underline{\underline{　\frac{5}{18}　}}
\end{eqnarray}\)

解答には座標をそれぞれ求めた経緯と、
台形の面積から\(\,a\,\)を求めたことを書いておけば良いです。

第３問１次関数と連立方程式

\(\,\large{3}\,\)
(1)は\(\,\mathrm{A}\,\)問題と同じで一次関数。
(2)は連立方程式の基本問題です。

問題の条件は自分で読み取っておいて下さい。
(1)
加湿器は強モードだけの使用で、
毎分\(\,\mathrm{6\,mL}\,\)でタンクの水は減ります。
（変化の割合が\(\,-6\,\)ということです。）
①
（ア）
\(\hspace{10pt}840-6\times 3=\,840-18=\underline{　822　}\)
（イ）
\(\hspace{10pt}840-6\times 9=840-54=\underline{　786　}\)
②
使用前のタンクの水\(\,840\,\)が\(\,y\,\)切片になります。
\(\hspace{10pt}\underline{　y=-6\,x+840　}\)
③
②の関数において\(\,y=450\,\)となるときの\(\,x\,\)を求めます。
　\(\begin{eqnarray}
-6x+840&=&450\\
-6\,x&=&-390\\
x&=&\underline{　65　}
\end{eqnarray}\)

これを文章題にしたのが\(\,\mathrm{A}\,\)問題です。（答えは同じ。）
(2)
今度は強モードと弱モードを両方使います。
　強モード：毎分\(\,\mathrm{6\,mL}\,\)減り\(\,s\,\)分間使用
　弱モード：毎分\(\,\mathrm{2\,mL}\,\)減り\(\,t\,\)分間使用

合計で\(\,\color{red}{192}\,\)分間使用し、\(\,\mathrm{\color{blue}{840}\,mL}\,\)減ったことになるので、
　\( \begin{cases}
\hspace{4pt} s\,+\,t=\color{red}{192}\\
\hspace{4pt} 6\,s+2\,t=\color{blue}{840}
\end{cases}\)

これを解くと
　\(\hspace{10pt}s=\underline{　114　}\,,\,t=\underline{　78　}\)

連立方程式の解き方はが減法でも代入法でもどちらでも良いです。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

単位は１つなので整数と考えても良いですが、
分数の可能性もあるので計算は確実に行いましょう。

文字２つなので時間と水の量の２つで方程式を立てれば後は計算だけです。

第４問図形総合問題

\(\,\large{4}\,\)
平面と立体の図形問題２つがあります。
※いずれも長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。
\(\,\mathrm{［Ⅰ］}\,\)
条件は問題から読み取れるので図で確認しましょう。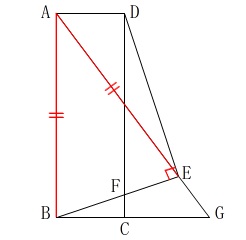(1)
相似の証明です。
　\(\,\mathrm{△AED}\,\)∽\(\,\mathrm{△GBE}\,\)
分かることを図の中で示して証明を終わらせておくと良いです。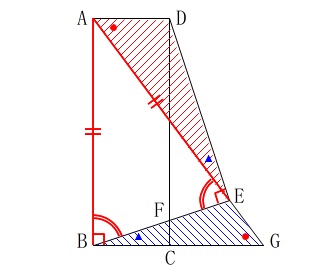\(\,\mathrm{△ABE}\,\)は二等辺三角形だから底角が等しくなる事がポイントです。
長方形だから\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BG}\,\)で錯角が等しくなるので
\(\hspace{10pt}\mathrm{\color{red}{∠EAD}}=\mathrm{\color{red}{∠BGE}}　･･･①\)
二等辺三角形の底角は等しいから
\(\hspace{10pt}\mathrm{∠ABE}=\mathrm{∠AEB}\)
等しい角を\(\,90°\,\)から引くことになるので
\(\hspace{10pt}\mathrm{\color{blue}{∠AED}=\color{blue}{∠GBE}}　･･･②\)
\(\,①②\,\)から「２組の角がそれぞれ等しい。」という相似条件がそろいます。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

相似条件をそろえる記述をルール通りしていれば書き方は好きにしていいですよ。
※
この問題は読み取れることは他にもたくさんありますが、
証明に必要なことだけを示しておきました。
①
辺\(\,\mathrm{AD}\,\)の長さを求めます。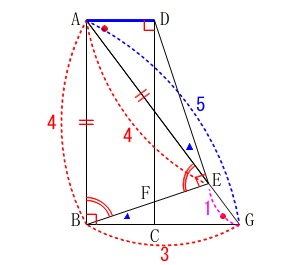(1)から\(\,\mathrm{△AED}\,\)∽\(\,\mathrm{△GBE}\,\)です。　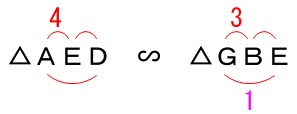\(\begin{eqnarray}
\mathrm{AE:GB}&=&\mathrm{AD:GE}\\
\color{red}{4}:\color{red}{3}&=&\mathrm{AD}:\color{magenta}{1}\\
3\times \mathrm{AD}&=&4\\
\mathrm{AD}&=&\underline{\underline{　\frac{4}{3}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)
(2)
長さが出てきます。
\(\hspace{10pt}\mathrm{AB}=4\,,\,\mathrm{BG}=3\)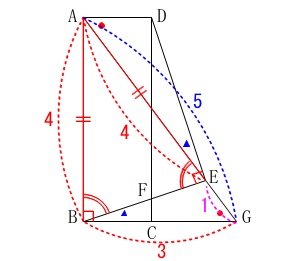\(\,\mathrm{△ABG}\,\)は直角三角形で三平方の定理から
\(\hspace{10pt}\mathrm{AG}=\color{blue}{5}\)
また、\(\,\mathrm{△ABE}\,\)は二等辺三角形なので
\(\hspace{10pt}\mathrm{AB=AE}=\color{red}{4}\,,\,\mathrm{EG}=\color{magenta}{1}\)
（ここまでは図に示してあります。）
②
線分\(\,\mathrm{FC}\,\)の長さを求めますが、
方針がいろいろあるので迷うかもしれません。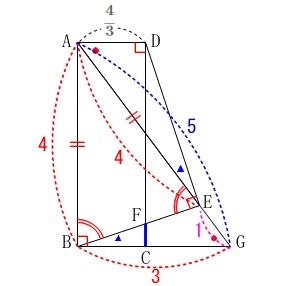全ての線分の長さは出てきますので、
思い立った方針で突っ走って良いと思います。

簡単にですがいくつか説明しておきます。
※
途中の簡単な計算は省略するので自分で求めておいて下さい。
というか、全ての線分を求めると良い計算練習になると思いますよ。

線分\(\,\mathrm{AG}\,\)と\(\,\mathrm{DC}\,\)の交点を\(\,\mathrm{H}\,\)とすると、
\(\,\mathrm{△ABG}\,\)と\(\,\mathrm{△HDA}\,\)は相似なので
\(\hspace{10pt}\displaystyle \mathrm{DH}=\color{red}{\frac{16}{9}}\,,\,\mathrm{AH}=\frac{20}{9}\)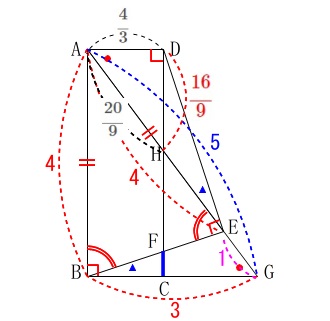対頂角が等しいから
\(\,\mathrm{△FCB}\,\)∽\(\,\mathrm{FED}\,\)が言えるので
\(\hspace{10pt}\mathrm{\color{blue}{∠HED}}=\mathrm{\color{blue}{∠HDE}}\)
さらに、平行線の錯角が等しいことから
\(\hspace{10pt}\mathrm{\color{red}{∠HEF}}=\mathrm{\color{red}{∠HFE}}\)
これらのことから\(\,\mathrm{△HDE}\,\)と\(\,\mathrm{△HFE}\,\)は二等辺三角形で
\(\hspace{10pt}\displaystyle \mathrm{HD=HE=HF}=\color{red}{\frac{16}{9}}\)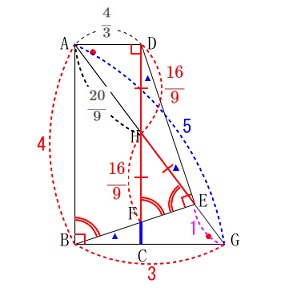よって、
\(\hspace{10pt}\displaystyle \mathrm{FC}=4-\color{red}{\frac{16}{9}}\times 2=\underline{\underline{　\frac{4}{9}　}}\mathrm{cm}\)

これは①からの流れで出てくる方針ですね。
もう一つだけ説明をおきます。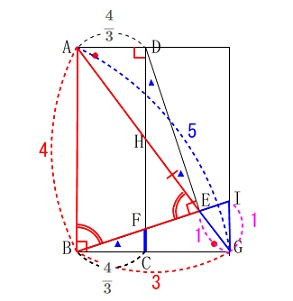\(\,\mathrm{BE}\,\)を延長した線と\(\,\mathrm{G}\,\)から\(\,\mathrm{AB}\,\)と平行な線との交点を\(\,\mathrm{I}\,\)とすると、
\(\,\mathrm{\color{red}{△ABE}}\,\)∽\(\,\mathrm{\color{blue}{△GIE}}\,\)（相似比\(\,\color{blue}{④}:\color{blue}{①}\)）
なので線分\(\,\mathrm{\color{magenta}{GI}}=\color{magenta}{1}\,\)（\(\,\mathrm{AB=\color{red}{4}}\,\)です。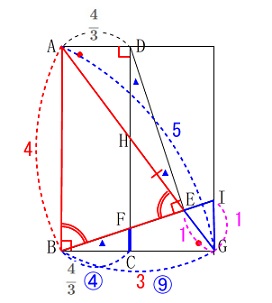）さらに、
\(\hspace{10pt}\displaystyle \mathrm{BC:BG}=\frac{4}{3}:\color{red}{3}=\color{blue}{4}:\color{blue}{9}\)
よって、
\(\hspace{10pt}\displaystyle \mathrm{FC}=\mathrm{\color{magenta}{GI}}\times \frac{\color{blue}{4}}{\color{blue}{9}}=\underline{\underline{　\frac{4}{9}　}}\mathrm{cm}\)

他にも点\(\,\mathrm{E}\,\)から線分\(\,\mathrm{BG}\,\)に垂線を下ろしても良いですね。

とにかく、条件から全ての線分が分かるので時間があるときに出してみて下さい。
かなり応用が利くようになりますよ。（たぶん。）

問題として線分\(\,\mathrm{BE}\,\)と線分\(\,\mathrm{DE}\,\)の長さも加えておくと良いです。
※
ここまでさんざんヒントを書き出しているので簡単ですが、
１からとなるとかなりの作業量に感じると思います。
\(\,\mathrm{［Ⅱ］}\,\)
立体図形の長さと体積までの問題です。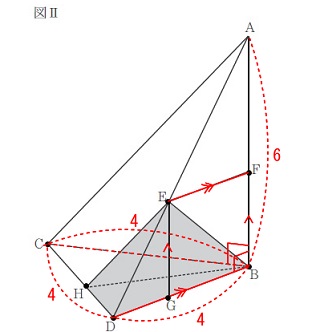わかりにくい図ですが\(\,\mathrm{△BCD}\,\)は正三角形です。
また直線\(\,\mathrm{AB}\,\)は面\(\,\mathrm{BCD}\,\)と垂直なので\(\,\mathrm{BD}\,\)や\(\,\mathrm{CB}\,\)とも垂直です。
(3)
線分\(\,\mathrm{EH}\,\)とねじれの位置にある辺を選びます。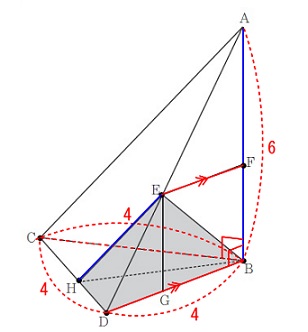答え\(\hspace{10pt}\underline{　ア　}辺\,\mathrm{AB}\,\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

ねじれの位置の意味は確認しておきましょう。
線分\(\,\mathrm{EH}\,\)は延長しても直線\(\,\mathrm{AB}\,\)とは交わりません。
(4)
条件が加わります。
\(\hspace{10pt}\mathrm{EF=EG}\)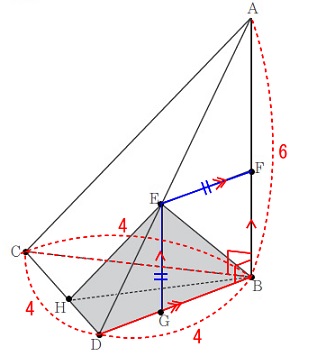四角形\(\,\mathrm{EGBF}\,\)は\(\,\mathrm{∠ABD=90°}\,\)なので正方形です。
（ひし形＋長方形）
①
線分\(\,\mathrm{EG}\,\)の長さを求めるので、
\(\hspace{10pt}\mathrm{EG}=\color{red}{x}\)
とします。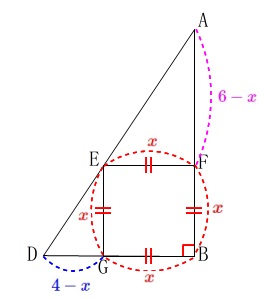線分の長さはそれぞれ
\(\hspace{10pt}\mathrm{EG=GB=BF=EF}=\color{red}{x}\)
\(\hspace{10pt}\mathrm{GD}=\color{blue}{4-x}\)
\(\hspace{10pt}\mathrm{AF}=\color{magenta}{6-x}\)
となるので相似を使えばすぐに求まります。

相似はどれでも良いですが、
\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△EGD}\,\)を使います。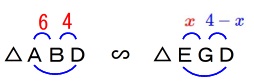　\(\begin{eqnarray}
\mathrm{AB:BD}&=&\mathrm{EG:GD}\\
\color{red}{6}:\color{red}{4}&=&\color{red}{x}:(\color{blue}{4-x})\\
4x&=&6(4-x)\\
4x&=&24-6x\\
10x&=&24\\
x&=&\frac{24}{10}=\underline{\underline{　\frac{12}{5}　}}\mathrm{cm}
\end{eqnarray}\)

利用するのは\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△ADB}\,\)でも、
\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△EDG}\,\)でも良いですよ。
同じ結果が出るのでやってみて下さい。
②
立体\(\,\mathrm{EHDB}\,\)の体積です。

底面は\(\,\mathrm{△BHD}\,\)で高さは\(\,\displaystyle \mathrm{EG}=\color{blue}{\frac{12}{5}}\,\)です。
ごちゃごちゃするので書いていませんでしたが、
辺\(\,\mathrm{AC}\,\)と辺\(\,\mathrm{EH}\,\)は平行です。
①の結果から
\(\hspace{10pt}\displaystyle \mathrm{GD}=4-\frac{12}{5}=\frac{8}{5}\)
\(\hspace{10pt}\displaystyle \mathrm{AF}=6-\frac{12}{5}=\frac{18}{5}\)
いずれにしても
\(\hspace{10pt}\mathrm{AE:ED}=3:2\)
となるので
\(\hspace{10pt}\mathrm{CH:HD}=\color{red}{③}:\color{red}{②}\)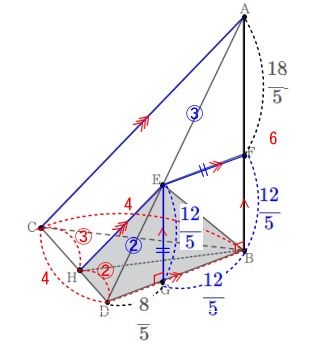このことから
　\(\begin{eqnarray}
\mathrm{DC:DH}&=&(\color{red}{②}+\color{red}{③}):\color{red}{②}\\
4:\mathrm{DH}&=&5:2\\
5\times \mathrm{DH}&=&4\times 2\\
\mathrm{\color{magenta}{DH}}&=&\color{magenta}{\frac{8}{5}}
\end{eqnarray}\)
これは\(\,\mathrm{△HDB}\,\)の底辺とみることができます。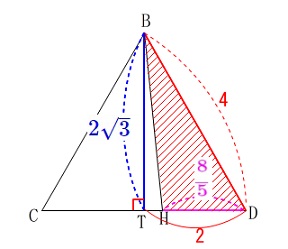\(\,\mathrm{△HDB}\,\)の高さは\(\,\mathrm{△BCD}\,\)の高さでもあるので、
三角定規の辺の比から垂線の長さ\(\,\mathrm{BT}\,\)は
\(\hspace{10pt}\displaystyle \mathrm{\color{blue}{BT}}=\color{blue}{2\sqrt{3}}\)

よって底面積は
　\(\begin{eqnarray}
\mathrm{\color{red}{△HDB}}&=&\frac{1}{2}\times \mathrm{\color{magenta}{DH}}\times \mathrm{\color{blue}{BT}}\\
&=&\frac{1}{2}\times \color{magenta}{\frac{8}{5}}\times \color{blue}{2\sqrt{3}}\\
&=&\color{red}{\frac{8\sqrt{3}}{5}}
\end{eqnarray}\)
（この計算は２行目で止めておいても良いです。）
高さは\(\,\mathrm{EG}\,\)なので求める体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times \mathrm{\color{red}{△HDB}}\times \mathrm{EG}\\
&=&\frac{1}{3}\times \color{red}{\frac{8\sqrt{3}}{5}}\times \frac{12}{5}\\
&=&\underline{\underline{　\frac{32\sqrt{3}}{25}　}}\,\mathrm{cm^3}
\end{eqnarray}\)
（線分\(\,\mathrm{EG}\,\)の長さは①の答えです。）

空間図形攻略の基本通り作業していれば問題ないですね。

以上です。

⇒　大阪府公立高校入試数学の過去問と解答解説

大阪府の数学は\(\,\mathrm{C}\,\)問題もありますが、
\(\,\mathrm{A\,,\,B}\,\)問題の基本から標準までがきっちり理解できていることが前提です。

先ずは\(\,\mathrm{A}\,\)問題の基本的な用語と作業からおさえておきましょう。