2022年(令和4年)度大阪府公立高校入試の数学A問題と解説

２０２２年(令和４年)度大阪府公立高校入試の数学Ａ問題と解説です。
昨年度は除外された分野がありましたが、
今年度は例年通りの基本問題による４問構成です。
基本をしっかりおさえておけば良いので応用に時間をかける必要はありません。
ここでは基本的な考え方を簡単にですが解説しておきます。

2022年(令和4年)度大阪府公立高校入試の数学A問題

大阪府立高校入試Ａ問題、令和４年度の問題です。

⇒　令和4年度大阪府公立高校入試の数学A問題

\(\,1\,\)から\(\,4\,\)までの大問\(\,4\,\)問の構成は例年通りです。
解答用紙は省いてありますので、解答用紙の形式が見たい人は大阪府の公式ページで確認できます。

2022年(令和4年)度大阪府公立高校入試の数学A問題の解説

『覚え太郎』で十分満点がとれますので解説は簡単に済ませます。

第１問

\(\,\large{1}\,\)
計算問題６つです。
(1)
　\(\hspace{10pt}-2-(-12)\\
=-2+12\\
=\underline{　10　}\)

負の数を引くことは正の数を足すことになります。
正の数負の数の計算は数直線上で考えると分かり易いですよ。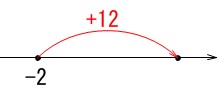正の数を足すときは右に移動します。

(2)
　\(\hspace{10pt}\displaystyle 27\times \left(-\frac{5}{9}\right)\\
\displaystyle =-27\times \frac{5}{9}\\
=\underline{　-15　}\)

全体の符号を先に考えて、約分です。

(3)
　\(\hspace{10pt}40-7^2\\
=40-7\times 7\\
=40-49\\
=\underline{　-9　}\)

計算順序を間違えないようにしましょう。
（かっこ）がないので掛け算部分が先です。

(4)
　\(\hspace{10pt}x-3+6(x+1)\\
=x-3+6x+6\\
=\underline{　7x+3　}\)

展開する２行目は暗算しない方がミスが減ります。

(5)
　\(\hspace{10pt}48x^3\div 8x\\
\displaystyle =48x^3\times \frac{1}{8x}\\
=\underline{　6x^2　}\)

割り算は逆数の掛け算で処理します。
これは暗算できる計算ですが、
少し複雑になってきても同じ処理で進めることができます。

(6)
　\(\hspace{10pt}\sqrt{12}+9\sqrt{3}\\
=\sqrt{\color{red}{2^2\times 3}}+9\sqrt{3}\\
=2\sqrt{3}+9\sqrt{3}\\
=\underline{　11\sqrt{3}　}\)

素因数分解は練習の度合いで暗算できるようになりますが、
ミスするともったいないのであまり暗算はしない方が良いです。

第２問

\(\,\large{2}\,\)
小問が１０題あります。
(1)
　\(\hspace{10pt}-2\times (-6)+14\\
=12+14\\
=\underline{　26　}\)

代入するときは正の数でも負の数でも（かっこ）をつけて代入、が良いですね。

(2)
\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)を引きます。
　\(\hspace{10pt}5.3-(-0.4)\\
=5.3+0.4\\
=\underline{　5.7　}℃\)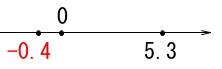負の数を引くことになるので注意しましょう。

(3)
不等式を作ります。

１つの袋に\(\,a\,\)個入った袋３つの個数の合計は
　\(\hspace{10pt}a\times 3\)
これが２０個より多いので
　\(\hspace{10pt}\underline{　3\,a\,＞\,20　}\)

この問題では選ぶ答えの中にありませんが、
不等号では「より」や「未満」のときは等号はつきません。
「以上」「以下」のときは等号がつきます。

(4)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 7x+y=19　･･･①\\
\hspace{4pt} 5x+y=11　･･･②
\end{cases}\)

代入法でも加減法でもどちらでも良いですよ。
ここでは\(\,y\,\)がきれいに消えるので加減法で処理しておきます。
　\(\hspace{20pt}7x+y=19\\
\underline{　-)\,5x+y=11　}\\
\hspace{20pt}\,2x\hspace{20pt}=8\\
\hspace{48pt}x=4\)

\(\,①②\,\)のどちらでも良いので代入して\(\,y\,\)を求めます。
ここでは\(\,①\,\)に代入します。
　\(\begin{eqnarray}\displaystyle
7\times (4)+y&=&19\\
28+y&=&19\\
y&=&19-28\\
&=&-9
\end{eqnarray}\)

答え　\(\,\underline{　x=4\,,\,y=-9　}\,\)

連立方程式を解くときの基本は一文字消去です。

(5)
今度は２次方程式を解きます。
　\(\hspace{4pt}x^2-8x+15=0\)

左辺は因数分解できそうなので因数分解から試します。
　\(\begin{eqnarray}\displaystyle
x^2-8x+15&=&0\\
(x-3)(x-5)&=&0\\
x&=&\underline{　3\,,\,5　}
\end{eqnarray}\)

⇒　２次方程式を解の公式で解く問題の見分け方と例題

因数分解できないときは解の公式を利用すれば良いです。

(6)
中央値を求めます。

７人のデータがあるので小さい順に並べたとき、
（大きい順でも良いです。）
４番目になる人のデータが中央値です。
　\(\hspace{4pt}26\,,\,27\,,\,27\,,\,\color{red}{28}\,,\,30\,,\,31\,\,,32\,\)

答え　\(\,\underline{　28　回　}\,\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値については現行課程で小学校の内容ですが、
ずっと必要ですので必ず復習しておきましょう。

(7)
確率です。

２つの箱に入ったカード
　\(\,\mathrm{A}\,\)：\(\,\color{red}{2}\,,\,\color{red}{3}\,,\,\color{red}{4}\,\)
　\(\,\mathrm{B}\,\)：\(\,\color{blue}{4}\,,\,\color{blue}{6}\,,\,\color{blue}{8}\,\)
からそれぞれ１枚ずつを取り出したとき、
積が\(\,18\,\)になる確率を求めます。

樹形図で良いですよ。
ここでは積の場合を表にしておきます。
　\(\begin{array}{|c|c|c|c|} \hline
& \color{red}{2} & \color{red}{3} & \color{red}{4} \\ \hline
\,\color{blue}{4} \,& 8 & 12 & \color{magenta}{16} \\ \hline
\color{blue}{6} & 12 & 18 & 24 \\ \hline
\color{blue}{8} & \color{magenta}{16} & 24 & 32 \\ \hline
\end{array}\)

取り出し方の組み合わせは９通りあるので
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{2}{9}　}}\)

(8)
グラフから傾きと切片が英の数か負の数かを読み取ります。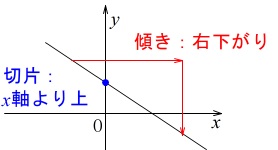傾きは右下がりなので負、
切片は\(\,x\,\)軸より上にあるので正です。

答え　\(\,\underline{　ウ　}\,\)

グラフから得られる情報はたくさんあるので、
読み取りは大切にしておきましょう。

(9)
比例定数を求めます。
　関数：\(\hspace{10pt}y=a\,x^2\)
これが点\(\,(\,-6\,,\,7\,)\,\)を通るので、
　\(\begin{eqnarray}\displaystyle
7&=&a\times (-6)^2\\
36\,a&=&7\\
a&=&\underline{\underline{　\frac{7}{36}　}}
\end{eqnarray}\)

比例\(\,y=ax\,\)、反比例\(\,\displaystyle y=\frac{a}{x}\,\)でも\(\,a\,\)は比例定数です。

(10)
立体図形の平行線と体積です。
与えられた長さは問題で確認して図に書き込んでください。
①
三角柱で辺\(\,\mathrm{AC}\,\)と平行な辺を探します。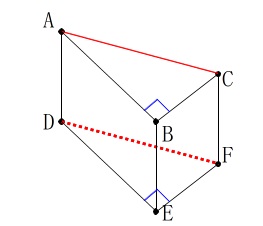平行な辺は辺\(\,\mathrm{DF}\,\)です。

答え　\(\,\underline{　エ　}\,\)

②
三角柱の体積を求めます。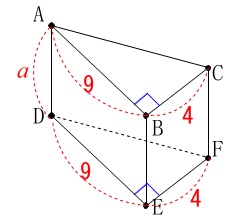底面は直角三角形で、
高さが\(\,a\,\)の三角柱なので求める体積を\(\,V\,\)とすると
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{2}\times 9\times 4\times a\\
&=&\underline{　18\,a　}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

\(\,\large{2}\,\)は以上です。

第３問

\(\,\large{3}\,\)
関数に見えますが、個数と高さの関係なので規則性の問題とも言えます。
(1)
個数と高さの関係を表します。
　コーンの個数：\(\,x\,\)　高さ：\(\,y\,\)
①
コーン１つで\(\,320\,\mathrm{mm}\,\)、
１つ積み重ねると\(\,15\,\mathrm{mm}\,\)増えるので順に埋めていけば答えは出ます。
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
x & 1 & 2 & 3 & 4 & \cdots & 8 & \cdots\\ \hline
y & 320 & 335 & 350 & \color{red}{365} & \cdots & \color{blue}{425} & \cdots\\ \hline
\end{array}\)

答え　\(\,ア：\underline{　365　}　イ：\underline{　425　}\,\)

これは自分で\(\,15\,\)を足していってください。
②が先に出れば足していく必要はありませが、
増え方をみていくことで②の関係式が出ます。

②
１つ増えると１５増えますが、
２個で１回１５増える、
３個で２回１５増える、、、
\(\,x\,\)個だと\(\,x-1\,\)回１５増えることになります。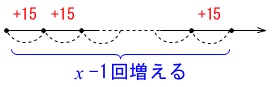
　\(\begin{eqnarray}\displaystyle
y&=&320+15(x-1)\\
&=&15x+305
\end{eqnarray}\)

答え　\(\hspace{4pt}\underline{　y=15x+305　}\)
　
\(\,x\,\)個積んだとき増えるのは\(\,x-1\,\)回だという事に注意しましょう。

(2)
高さから積んだ個数を求めますが、
(1)で関係式を出しているので利用します。

(2)では\(\,t\,\)個積んだときを考えているので
　\(\hspace{4pt}y=15t+305\)
高さは\(\,y\,\)のままでも良いです。

「\(\,y=620\,\)のとき\(\,t\,\)は？」
という問題になります。
　\(\begin{eqnarray}\displaystyle
620&=&15t+305\\
15t&=&315\\
t&=&\underline{　21　}
\end{eqnarray}\)

\(\,t\,\)は個数なので整数（自然数）で出なければ計算ミスしてますよ。

\(\,\large{3}\,\)は以上です。

第４問

\(\,\large{4}\,\)
図形基礎総合問題です。

長方形と条件があって、
角度、長さ、証明とありますので順に進めて行きます。

長さや条件は問題文から読み取って、
図に書き込んでおきましょう。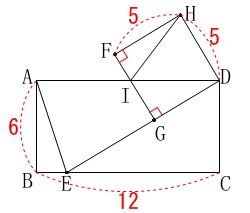(1)
角度を文字を用いて表します。
　\(\hspace{4pt}\mathrm{∠BEA}=a^{\circ}\)
とするときの\(\,\mathrm{∠BAE}\,\)です。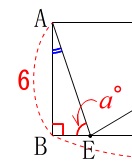\(\,\mathrm{△ABE}\,\)は直角三角形なので、
（\(\,\mathrm{∠ABE}\,\)は長方形の一角）
　\(\hspace{10pt}\mathrm{∠BAE}=\underline{　90-a　}度\)

三角形の内角の和が\(\,180°\,\)なので、
直角以外の残り２つの和は\(\,90°\,\)です。

問題に「内角\(\,\mathrm{∠BEA}\,\)」などと書かれていますが、
点を３つ使って表しているので内角も外角も関係ありません。
ただ、角度の表記が「°」なのか「度」なのかはっきりして欲しいところですね。
問題は「°」解答は「度」です。

(2)
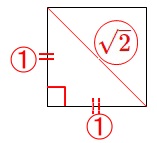
正方形の対角線の\(\,\mathrm{FD}\,\)長さです。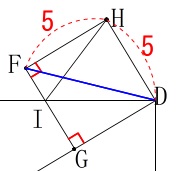三角定規の比と同じになりますね。
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{FG}:FD}&=&1:\sqrt{2}\\
\color{red}{5}:\mathrm{FD}&=&1:\sqrt{2}\\
\mathrm{FD}&=&\underline{　5\sqrt{2}　}(\,\mathrm{cm}\,)
\end{eqnarray}\)

三平方の定理でも良いですよ。
　\(\begin{eqnarray}\displaystyle
\mathrm{FD^2}&=&\mathrm{FG^2+GD^2}\\
&=&5^2+5^2\\
&=&50\\
\mathrm{FD}&=&\pm \sqrt{50}\\
&=&\pm 5\sqrt{2}
\end{eqnarray}\)
長さなので\(\,\mathrm{FD\,＞\,0}\,\)だから
　\(\hspace{10pt}\mathrm{FD}=5\sqrt{2}\)

よく使うので三角定規の比は覚えておくと便利です。

(3)
相似の証明です。
　\(\,\mathrm{△DEC}\,\)∽\(\,\mathrm{△IDG}\,\)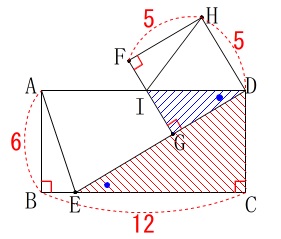長方形の対辺は平行なので、
錯角が等しく
　\(\hspace{4pt}\mathrm{∠DEC=∠IDG}\)
長方形、正方形の１つの角は直角なので
　\(\hspace{4pt}\mathrm{∠DCE=∠IGD}=90^{\circ}\)
「２組の角がそれぞれ等しい」
という相似条件がそろうので相似であることが分かります。

このことを〔証明〕の中で埋めていきますが、
合同、相似の証明では記号の順番もそろえるので注意しましょう。
（間違えていないか自分で解答を書いてみてください。）

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

図形における証明では図の中で終わらせておくことがポイントです。

(4)
条件が加わり線分の長さを求めますが、
最初に与えられた条件はそのままです。
　\(\hspace{4pt}\mathrm{EC}=10　(\mathrm{cm})\)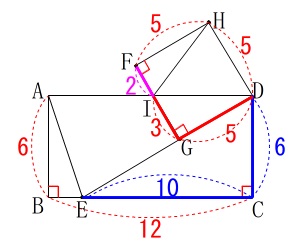(3)で証明した相似から
　\(\begin{eqnarray}\displaystyle
\mathrm{EC:DC}&=&\mathrm{DG:IG}\\
\color{blue}{10}:\color{blue}{6}&=&\color{red}{5}:\color{red}{3}
\end{eqnarray}\)
（\(\,\mathrm{DG}\,\)は正方形の１辺です。）
ここで
　\(\begin{eqnarray}\displaystyle
\mathrm{IF}&=&\mathrm{FG-IG}\\
&=&5-3\\
&=&\color{magenta}{2}
\end{eqnarray}\)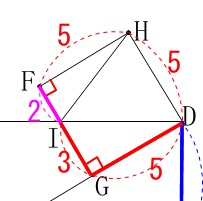\(\,\mathrm{△IHF}\,\)は直角三角形なので三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{IH^2}&=&\mathrm{IF^2+HF^2}\\
&=&\color{magenta}{2}^2+\color{red}{5}^2\\
&=&29
\end{eqnarray}\)
これから
　\(\hspace{10pt}\mathrm{IH}=\pm \sqrt{29}\)
線分\(\,\mathrm{IH}\,\)は長さなので\(\,\mathrm{IH\,＞\,0}\,\)だから
　\(\hspace{10pt}\mathrm{HI}=\underline{　\sqrt{29}　}(\,\mathrm{cm}\,)\)