2022年(令和4年)度高知県公立高校入試の【A日程】の数学の問題と解説です。
基本重視の問題がそろっていますのでミスを避けたいですね。
中盤から後半にかけて作業中心の問題になりますが、
作業自体も基本的なので自分の作業ができているかの確認をすると良いです。
2022年(令和4年)度高知県公立高校入試A日程の数学の問題
令和4年度高知県公立高校入試【A日程】の数学の問題です。
⇒ 令和4年度高知県公立高校入試【A日程】の数学の問題PDF
問題は大問で\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。
2022年(令和4年)度高知県公立高校入試A日程の数学の解説
2022年(令和4年)度高知県公立高校入試【A日程】の数学の解説です。
\(\,50\,\)点満点なので1問1問の配点比率が大きいので、
取れる問題はミスの無いように確実に取り組みましょう。
第1問計算が主な小問集合
\(\color{black}{\fbox{1}}\)
計算や方程式、資料や図形などの基本問題が(1)から(8)まであります。
(1)
計算問題が4問あります。
①
\(\hspace{10pt}3+(-6)-(-8)\\
=3-6+8\\
=\underline{ 5 }\)
できるだけ暗算をさけて確実に進めましょう。
②
\(\hspace{10pt}\displaystyle \frac{5x-y}{3}-\frac{x-y}{2}\\
\displaystyle =\frac{2(5x-y)-3(x-y)}{6}\\
\displaystyle =\frac{10x-2y-3x+3y}{6}\\
\displaystyle =\underline{\underline{ \frac{7x+y}{6} }}\)
分数計算は通分して分子の計算に集中ですね。
③
\(\hspace{10pt}8a^2b\div (-2a^3b^2)\times (-3a)\\
\displaystyle =\frac{8a^2b\times 3a}{2a^3b^2}\\
\displaystyle =\underline{\underline{ \frac{12}{b} }}\)
全体の符号を先ず見て、
後は割り算は逆数の掛け算として処理すれば良いだけです。
\(\hspace{10pt}8a^2b\div (-2a^3b^2)\times (-3a)\\
\displaystyle =8a^2b\times \frac{1}{2a^3b^2}\times 3a\\
\displaystyle =\underline{\underline{ \frac{12}{b} }}\)
でも同じですが、
\(\,\div\,\)の直後を分母に回せばややこしい計算でも見やすいですよ。
④
\(\hspace{10pt}\displaystyle \frac{12}{\sqrt{6}}+3\sqrt{3}\times (-\sqrt{2})\\
\displaystyle =\frac{12\times \sqrt{6}}{\sqrt{6}\times \sqrt{6}}-3\sqrt{6}\\
\displaystyle =\frac{12\sqrt{6}}{6}-3\sqrt{6}\\
=2\sqrt{6}-3\sqrt{6}\\
=\underline{ -\sqrt{6} }\)
分母の有理化やルートの中の簡素化は慣れれば暗算できるようになりますが、
先を急いでミスだけはしないようにしましょう。
(2)
条件を満たす関係式を表します。
問題文の通りに関係式を立てれば良いだけです。
男子生徒\(\,a\,\)人のうちの\(\,\displaystyle \frac{2}{5}\,\)と女子生徒\(\,b\,\)人のうちの\(\,\displaystyle \frac{1}{4}\,\)、
合わせると35人であった。
\(\hspace{4pt}\displaystyle \frac{2}{5}\,a+\frac{1}{4}\,b=35\)
関係式はこれでいいです。
ただし、問題は\(\,b\,\)を\(\,a\,\)の式で表すよう指示がありますので、
\(\,b=\,\cdots\,\)の形で答えます。
\(\begin{eqnarray}\displaystyle
8a+5b&=&700\\
5b&=&700-8a\\
b&=&140-\frac{8}{5}\,a
\end{eqnarray}\)
答え \(\displaystyle \underline{\underline{ b=140-\frac{8}{5}\,a }}\)
⇒ 小数や分数が係数にある連立方程式をはやく解く解き方のコツ
文字が\(\,x\,\)ではありませんが1次方程式の処理になります。
(3)
\(\,x\,>\,0\,\)において\(\,x\,\)が増加すると\(\,y\,\)が減少する関数を選びます。
グラフの大まかな形を書けばすぐに見つかります。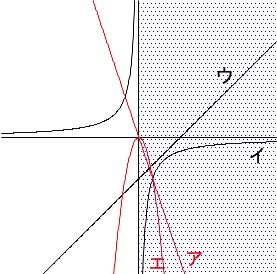 右に移動するにつれて下がるグラフを選びます。
右に移動するにつれて下がるグラフを選びます。
答え \(\,\underline{ ア\,,\,エ }\,\)
関数の特性を知ってしまえばグラフを見なくてもわかりはしますが、
関数の問題ではグラフをイメージしながら考えるようにしましょう。
(4)
解の公式を利用せずに、
平方完成型で処理して2次方程式を解きます。
\(\begin{eqnarray}\displaystyle
x^2+2x-14&=&0\\
x^2+2x&=&14\\
x^2+2x\color{red}{+1}&=&14\color{red}{+1}\\
(x+1)^2&=&15\\
x+1&=&\pm \sqrt{15}\\
x&=&\underline{ -1\pm \sqrt{15} }
\end{eqnarray}\)
途中の過程も書くように指示がありますので解だけではダメですよ。
平方完成するときに両辺に\(\,\color{red}{+1}\,\)して
\(\,(x+1)^2\,\)の形を作ることがポイントですね。
定数項を移項する前に変形しても良いです。
\(\begin{eqnarray}\displaystyle
x^2+2x-14&=&0\\
x^2+2x\color{red}{+1}-14\color{blue}{-1}&=&0\\
(x+1)^2&=&15
\end{eqnarray}\)
後は同じです。
どちらでも良いですよ。
⇒ 2次方程式の解の公式の二通りの求め方と文章題の解き方(中学3年)
解の公式も同じ形で導く事になります。
(5)
関数の定義域と値域の問題です。
関数\(\,y=3\,x^2\,\)が\(\,y\,\)軸対称だということをイメージできれば、
\(\,x=a\,\)のときに\(\,y=12\,\)となることが分かります。
イメージだけでなくグラフを描いて考えると早いです。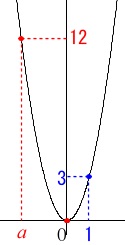 \(\,x\,\)の最大値\(\,x=1\,\)のとき\(\,y=3\,\)なので、
\(\,x\,\)の最大値\(\,x=1\,\)のとき\(\,y=3\,\)なので、
\(\,x=a\,\)のとき最大値\(\,12\,\)となるしかありません。
\(\begin{eqnarray}\displaystyle
12&=&3\times (\,a\,)^2\\
a^2&=&4\\
a&=&\pm 2
\end{eqnarray}\)
条件から\(\,a\,≦\,1\,\)なので
\(\hspace{10pt}a=\underline{ -2 }\)
(6)
角度を求める問題です。
分かる角度を書き込んでいけば見えてきますよ。
\(\hspace{10pt}\mathrm{∠ABE}=\color{red}{34°}\)
\(\hspace{10pt}\mathrm{∠BAD}=90°\)
\(\hspace{10pt}\mathrm{∠BCE}=\color{blue}{56°}\)
\(\hspace{10pt}\mathrm{∠BEC}=80°\)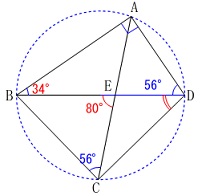 三角形の内角の和から\(\,\mathrm{∠ADB=\color{blue}{56°}}\,\)なので、
三角形の内角の和から\(\,\mathrm{∠ADB=\color{blue}{56°}}\,\)なので、
\(\hspace{4pt}\mathrm{∠BCE=∠ADB}=\color{blue}{56^{\circ}}\)
となるので円周角の定理の逆から、
四角形\(\,\mathrm{ABCD}\,\)は円に内接していて、対角線\(\,\mathrm{BD}\,\)は直径になっています。
後は一つひとつ分かる角度を書き込んで行けば良いです。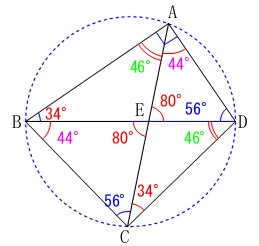 三角形の内角の和からでも良いですし、
三角形の内角の和からでも良いですし、
\(\hspace{4pt}\mathrm{∠BEC=∠BDC+∠ECD}\)
を利用しても良いです。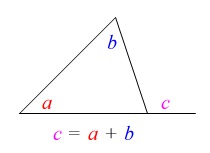 分かることを利用すれば何でも良いですよ。
分かることを利用すれば何でも良いですよ。
ただ、上に書き込んだ角度は全部自分で出しておいて下さい。
観て納得するのと、自分で確認するのとでは大きな違いがあります。
(7)
ヒストグラムから割合を求めます。
各階級の度数を書き出せばすぐに終わります。
ヒストグラムに書き込めば良いですが、
度数分布表にしておきます。
試験中にこの手間をかける必要はありませんよ。
\(\begin{array}{|c|c|} \hline
階級 & 度数 \\ \hline
160\,~\,170 & 2 \\ \hline
170\,~\,180 & 3 \\ \hline
180\,~\,190 & 4 \\ \hline
190\,~\,200 & 6 \\ \hline
200\,~\,210 & \color{red}{8} \\ \hline
210\,~\,220 & \color{red}{13} \\ \hline
220\,~\,230 & \color{red}{9} \\ \hline
230\,~\,240 & 5 \\ \hline
合計 & 50 \\ \hline
\end{array}\)
(階級は以上、未満で区切ってあります。)
度数合計は\(\,50\,\)なので
\(\hspace{10pt}\displaystyle \frac{\color{red}{8}+\color{red}{13}+\color{red}{9}}{50}\times 100\\
\displaystyle =\frac{30}{50}\times 100\\
=\underline{ 60 }%\)
度数合計は分かっているので、
関係する3つの階級の度数をヒストグラムに書き込んで足せば良いですよ。
(8)
作図です。
会員は『覚え太郎』図形編で確認して、といわなくても覚えているでしょう。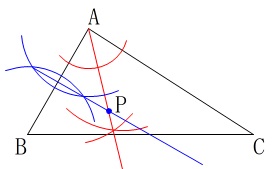 2辺から等しい距離にある点の集まりは角の二等分線、
2辺から等しい距離にある点の集まりは角の二等分線、
2点から等しい距離にある点の集まりは垂直二等分線です。
第2問規則性のある数字の列と文字式の関係
\(\color{black}{\fbox{2}}\)
規則性を読む文字式の基本問題です。
行と列がありますが問題に規則性が書いてあるので読み取りましょう。
・1つの行で右に1つ列が移動すると2増える。
・1つの列で下に1つ行が移動すると3増える。
\(\begin{array}{|c|c|c|c|c|} \hline
& 1\,列 & 2\,列 & 3\,列 & \cdots \\ \hline
1\,行 & 1 & 3 & 5 & \cdots \\ \hline
2\,行 & 4 & 6 & 8 & \cdots \\ \hline
3\,行 & 7 & 9 & 11 & \cdots\\ \hline
\vdots & \vdots & \vdots & \vdots & \vdots \\ \hline
\end{array}\)
これで十分です。
(1)
並んだ4つの数の関係が、
「右上の数と左下の数の積から、
左上の数と右下の数の積を引くと6となる。」
事を文字式を使って説明します。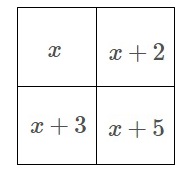 れいさんの説明を書き上げます。
れいさんの説明を書き上げます。
〔説明〕
(つづき)
右上の数字は\(\,x+2\,\)、下の数字は\(\,x+3\,\)、
右下の数字は左下の数字から2増えるので\(\,x+5\,\)とおける。
このとき右上の数と左下の数の積から、
左上の数と右下の数の積を引くと
\(\hspace{10pt}(x+2)(x+3)-x(x+5)\\
=x^2+5x+6-x^2-5x\\
=6\)
となる。
これは引き算の順序を間違えても、
6にならないので間違えようがないですね。
(2)
次は\(\,m\,\)行、\(\,n\,\)列にある数を\(\,m\,,\,n\,\)を使って表します。
行と列を一度に考えるとややこしいように見えるので、
別々に考えれば良いですよ。
問題の〔表の中の数を文字式で、、、〕
という部分にある5行目4列目の「19」は
\(\hspace{10pt}1\color{red}{+3+3+3+3}\color{blue}{+2+2+2}\\
=1+3\times 4+2\times 3\\
=19\)
これは先ず
\(\hspace{4pt}1\color{red}{+3+3+3+3}=1+3\times 4\)
を考えます。
一番左上から\(\,5\,\)行目まで下りると
\(\,4\,\)回\(\,\color{red}{+3}\,\)を足すことになります。
その数から\(\,4\,\)列目まで右に行くと
\(\,3\,\)回\(\,\color{blue}{+2}\,\)を足すことになります。
\(\hspace{10pt}1\color{red}{+3+3+3+3}\color{blue}{+2+2+2}\)
それが「19」の理由です。
これを一般化します。
\(\,1\,\)行から\(\,m\,\)行までは\(\,\color{red}{+3(m-1)}\,\)、
\(\,1\,\)列から\(\,n\,\)列までは+\(\,\color{blue}{2(n-1)}\,\)されます。
\(\begin{array}{|c|c|c|c|} \hline
& 1\,列 & \cdots & n\,列目 \\ \hline
1\,行 & 1 & \color{blue}{→} & 1\color{blue}{+2(n-1)}\\ \hline
\vdots & \color{red}{↓} & & \color{red}{↓} \\ \hline
m\,行 & 1+3(m-1) & \color{blue}{→} & 1\color{red}{+3(m-1)}\color{blue}{+2(n-1)}\\ \hline
\end{array}\)
よって、\(\,m\,\)行目\(\,n\,\)列目の数は
\(\hspace{10pt}1+3(m-1)+2(n-1)\\
=1+3\,m-3+2\,n-2\\
=\underline{ 3\,m+2\,n-4 }\)
行と列の移動はどちらが先でも良いですよ。
足される回数が\(\,m-1\,,\,n-1\,\)回という点がポイントでしょうか。
(整数の個数を数えるときと同じで「間隔」は1つ少ない。)
(3)
表の中に数字を書いていっても答えは出そうです。
考え方もいろいろありそうですが、
5列目に限定されているので(2)において\(\,n=5\,\)のときです。
5列目の\(\,m\,\)行目にある数は
\(\hspace{10pt}3m+2\times 5-4\\
=3\,m+6\)
これより上の3つの数を足すと(3ずつ少なくなっているので)
\(\hspace{10pt}(3m+6)+(3m+3)+(3m)+(3m-3)\\
=12\,m+6\)
これが\(\,222\,\)なので
\(\begin{eqnarray}\displaystyle
12\,m+6&=&222\\
12\,m&=&216\\
m&=&18
\end{eqnarray}\)
答え \(\,\underline{ 18 行目 }\,\)
二段階で考えると、
5列目の数を\(\,a-9\,,\,a-6\,,\,a-3\,,\,a\,\)とすると
この和が\(\,222\,\)なので
\(\begin{eqnarray}\displaystyle
4a-18&=&222\\
4a&=&240\\
a&=&60
\end{eqnarray}\)
\(\,60\,\)が5列目の\(\,m\,\)行目の数とみると
\(\begin{eqnarray}
9+3(m-1)&=&60\\
3m+6&=&60\\
3m&=&54\\
m&=&18
\end{eqnarray}\)
でも良いです。
カレンダーでも同じような問題があるので、
上下の増減には慣れていくと良いですね。
第3問確率
\(\color{black}{\fbox{3}}\)
さいころ2つの確率です。
進む順番は「あいうえお」の順にまわりますが、
五角形と考えてても同じですね。
ルールを確認しておくと、
①1回目は出たさいころの目の数だけ移動させる。
②2回目は出たさいころの目の数の3倍移動させる。
(①で移動したところから移動します。)
(1)
①②の移動後「あ」の位置にいる確率です。
さいころ2つなので36通り調べれば分かりますが、
少しやりやすいように「あいうえお」を数字に置き換えておきます。
「あ」は出発点なので\(\,0\,\)として、
5ずつ増えると「あ」に戻るので、
「あ」は\(\,0\,,\,\color{red}{5}\,,\,\color{red}{10}\,,\,\color{red}{15}\,,\,\color{red}{20}\,\)
同じように、
「い」は\(\,1\,,\,6\,,\,11\,,\,16\,,\,21\,\)
「う」は\(\,2\,,\,7\,,\,12\,,\,17\,,\,22\,\)
「え」は\(\,3\,,\,8\,,\,13\,,\,18\,,\,23\,\)
「お」は\(\,4\,,\,9\,,\,14\,,\,19\,,\,24\,\)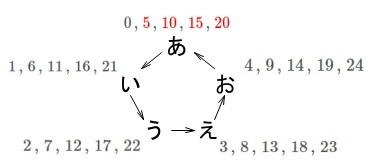 1回目は出た目、2回目は出た目の3倍なので、
1回目は出た目、2回目は出た目の3倍なので、
移動するのは最大で
\(\hspace{10pt}6+3\times 6=\,24\)
であることと、①②の移動後、
\(\,0\,,\,1\,,\,2\,,\,3\,\)という数字はないことを確認しておいて下さい。
樹形図で良いですが、
ここでは表で①②の移動後の数字を見ておきます。
縦の赤い数字が1回目の出た目、
横の青い数字が2回目の出た目です。
(青い数字は3倍して赤い数字に足します。)
\(\begin{array}{|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & 4 & 7 & \color{magenta}{10} & 13 & 16 & 19 \\ \hline
\color{red}{2} & \color{magenta}{5} & 8 & 11 & 14 & 17 & \color{magenta}{20} \\ \hline
\color{red}{3} & 6 & 9 & 12 & \color{magenta}{15} & 18 & 21 \\ \hline
\color{red}{4} & 7 & \color{magenta}{10} & 13 & 16 & 19 & 22 \\ \hline
\color{red}{5} & 8 & 11 & 14 & 17 & \color{magenta}{20} & 23 \\ \hline
\color{red}{6} & 9 & 12 & \color{magenta}{15} & 18 & 21 & 24 \\ \hline
\end{array}\)
これを書き上げるのはメンドウですが、
書いている途中で数字の増え方に気がつくと思います。
\(\,\color{magenta}{5\,の倍数}\,\)になるところだけに印をすれば良いですよ。
答え \(\hspace{4pt}\displaystyle \underline{\underline{ \frac{7}{36} }}\)
全てを調べるのは時間がかかりすぎるので、
1回目の場合分けで「あ」になるときだけをみていくと良いですね。
例えば1回目に出た目が\(\,\color{red}{1}\,\)のとき、
2回目は\(\,\color{blue}{3}\,\)でなければ「あ」ではありません。
\(\hspace{10pt}1+3\times \color{blue}{3}=\color{red}{10}\)
これを続けます。
(2)
①の移動後のこまのマスと、
②の移動後のこまのマスが異なる確率です。
上の表で確認しても良いですが、
①の移動後と②の移動後のこまのマスが同じときを考えると早いです。
①の移動後どこにあっても、
2回目のさいころの出た目が5のとき同じマスに移動します。
(5の倍数移動すると同じマスになる。)
よって、同じマスになる確率は\(\,\displaystyle \frac{1}{6}\,\)なので
異なるマスになるのは
\(\hspace{4pt}\displaystyle 1-\frac{1}{6}=\underline{\underline{ \frac{5}{6} }}\)
もちろん、
1回目に出た目が1のとき、2のとき、、、と調べても良いですよ。
ただ、異なる方を数えるのではなく、
反対の事象(余事象)となる同じマスにいる確率を1から引く方が断然早いです。
説明足りないかな?
先に進みます。
第4問動点と関数
\(\color{black}{\fbox{4}}\)
点が移動し垂線が切り取る長さの長さの関数です。
動点問題の基本通り進めます。
条件
記号や長さは問題にある通り図で示します。
点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)で点\(\,\mathrm{A}\,\)から\(\,\mathrm{D}\,\)まで移動します。
点\(\,\mathrm{P}\,\)を通り\(\,\mathrm{BD}\,\)に垂直な直線\(\,\ell\,\)が、
動き始めて\(\,x\,\)秒後切り取る長さ\(\,\mathrm{QR}\,\)を\(\,y\,\)とする。
※
長さの単位は\(\,\mathrm{cm}\,\)です。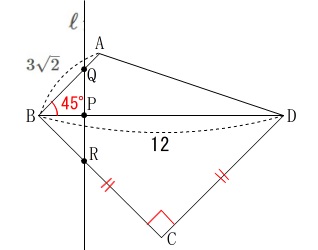 区間を分けたいので垂線を引いて、
区間を分けたいので垂線を引いて、
各線分の長さを出しておきます。
頂点\(\,\mathrm{A}\,\)と頂点\(\,\mathrm{C}\,\)から\(\,\mathrm{BD}\,\)に垂線を引き、
\(\,\mathrm{BD}\,\)との交点を\(\,\mathrm{S\,,\,T}\,\)とすると、
\(\hspace{4pt}\mathrm{BS=AS}=3\,,\,\mathrm{BT=CT}=6\)
となります。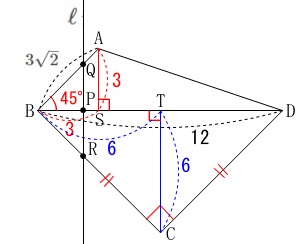 直角二等辺三角形が目立つので説明は必要ないでしょう。
直角二等辺三角形が目立つので説明は必要ないでしょう。
これから区間を、
\(\hspace{4pt}0\,≦\,x\,≦\,3\)
\(\hspace{4pt}3\,≦\,x\,≦\,6\)
\(\hspace{4pt}6\,≦\,x\,≦\,12\)
で考えれば良いことが分かります。
(変化の起こるところで区切ります。)
ここまでができれば後は相似を使うだけなので、
問題に合わせてみていきます。
(1)
\(\,x=3\,\)のときの\(\,y\,\)(\(\,\mathrm{QR}\,\)の長さ)の値を求めます。
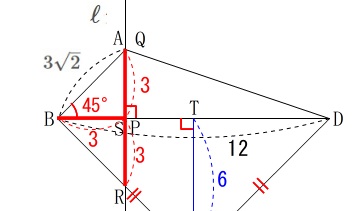 点\(\,\mathrm{P}\,\)が\(\,\mathrm{S}\,\)と重なるときで、
点\(\,\mathrm{P}\,\)が\(\,\mathrm{S}\,\)と重なるときで、
\(\,\mathrm{△BPR}\,\)も直角二等辺三角形だから
\(\begin{eqnarray}
y&=&\mathrm{QP+PR}\\
&=&\mathrm{AS+SR}\\
&=&3+3\\
&=&\underline{ 6 }(\mathrm{cm})
\end{eqnarray}\)
\(\,\mathrm{∠RBP}\,\)も\(\,45°\,\)です。
(2)
\(3\,≦\,x\,≦\,6\,\)のときの\(\,y\,\)を\(\,x\,\)の式で表します。。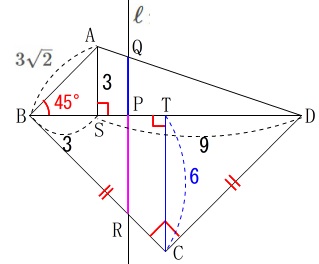 直線\(\,\mathrm{AD}\,\)が傾き\(\displaystyle \,-\frac{1}{3}\,\)の直線であることを利用して、
直線\(\,\mathrm{AD}\,\)が傾き\(\displaystyle \,-\frac{1}{3}\,\)の直線であることを利用して、
\(\,\mathrm{AB}\,\)を延長してみても良いですが、
後で別解として解説してみます。
ここでは相似で処理しておきましょう。
点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{ST}\,\)上にあるので、
\(\hspace{4pt}y=\mathrm{QP+PR}\)
において\(\,\mathrm{QP}\,\)と\(\,\mathrm{PR}\,\)を別に考えます。
\(\,\mathrm{△ASD}\,\)∽\(\,\mathrm{△QPD}\,\)を利用します。
\(\hspace{4pt}\mathrm{BP}=x\,,\,\mathrm{PD}=\color{red}{12-x}\)
\(\hspace{4pt}\mathrm{AS}=3\,,\,\mathrm{SD}=9\)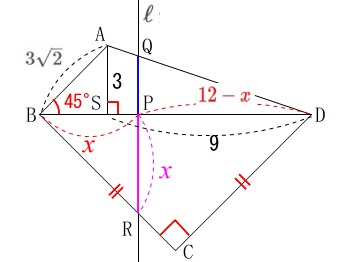 これから
これから
\(\begin{eqnarray}
\mathrm{AS:SD}&=&\mathrm{QP:PD}\\
3:9&=&\mathrm{QP}:(12-x)\\
\mathrm{QP}&=&\color{blue}{\frac{1}{3}(12-x)}
\end{eqnarray}\)
また、\(\,\mathrm{△BPR}\,\)が直角二等辺三角形であることから
\(\hspace{4pt}\mathrm{PR}=\color{magenta}{x}\)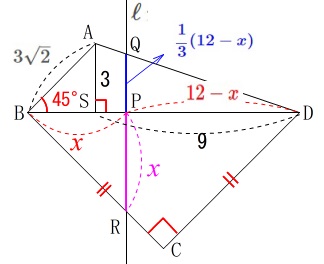 よって、
よって、
\(\begin{eqnarray}\displaystyle
y&=&\mathrm{QP+PR}\\
&=&\color{magenta}{x}+\color{blue}{\frac{1}{3}(12-x)}\\
&=&\frac{2}{3}x+4
\end{eqnarray}\)
答え \(\displaystyle \underline{ \,y=\frac{2}{3}x+4 }\,\)
(3)
\(\,y=4\,\)となる\(\,x\,\)を全て求めます。
3つの区間を全て調べれば良いことですが、
\(\,3\,≦\,x\,≦\,6\,\)のとき明らかに\(\,y\,≧\,6\,\)なので除外します。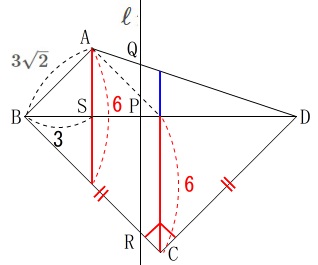 また、\(\,6\,≦\,x\,≦\,12\,\)のとき、
また、\(\,6\,≦\,x\,≦\,12\,\)のとき、
\(\,\mathrm{PR=PD}=\color{red}{12-x}\,\)
であることは確認しておいて下さい。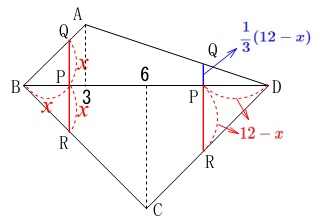
ⅰ)
\(\,0\,≦\,x\,≦\,3\,\)のとき\(\,\mathrm{QR}=2x\,\)なので
\(\begin{eqnarray}\displaystyle
2x&=&4\\
x&=&2
\end{eqnarray}\)
ⅱ)
\(\,0\,≦\,x\,≦\,3\,\)のとき
\(\begin{eqnarray}\displaystyle
\mathrm{QR}&=&\mathrm{QP+PR}\\
&=&\frac{1}{3}(12-x)+(12-x)\\
&=&16-\frac{4}{3}x
\end{eqnarray}\)
なので
\(\begin{eqnarray}\displaystyle
16-\frac{4}{3}x&=&4\\
48-4x&=&12\\
x&=&9
\end{eqnarray}\)
答え \(\,x=\underline{ 2\,,\,9 }\,\)
\(\color{black}{\fbox{4}}\)は以上です。
第4問動点と関数(別解)
普通は条件の図から図形問題だと考えると思います。
しかし、これを関数としてみる事もできますので、
別解として簡単に説明しておきます。
表題に上げている通り関数の問題なので、
グラフを利用してみていきましょう。
軸をどこにとるかは人によって変わるでしょうが、
ここでは点\(\,\mathrm{B}\,\)を原点としておきます。
各線分を直線と考えたときの式は
直線\(\,\mathrm{AB}\,\):\(y\,=\,x\)
直線\(\,\mathrm{BC}\,\):\(y\,=\,-x\)
直線\(\,\mathrm{AD}\,\):\(\,\displaystyle y=-\frac{1}{3}\,x+4\)
直線\(\,\mathrm{DC}\,\):\(y\,=\,x-12\)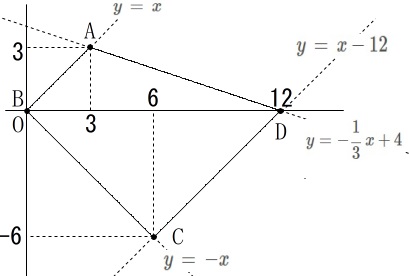 2点を探して求めれば直線の式は求まるでしょう。
2点を探して求めれば直線の式は求まるでしょう。
後は、(1)から問題に合わせてやってみて下さい。
これは座標の軸をどこに設定するかで変わりますので、
解説はここまでとしておきます。
相似を利用しようとグラフを利用しようとどちらでも良いです。
第5問
\(\color{black}{\fbox{5}}\)
比例定数、直線の式を求める関数問題です。
今度はグラフがありますので普通に利用しましょう。
問題にある条件
関数\(\,①\,\):\(\,y=ax^2\,\)\(\,(\,a\,>\,0\,)\)
関数\(\,②\,\):\(\,y=2x^2\,\)
点\(\,\mathrm{A}\,\):\(\,(\,6\,,\,12\,)\,\)
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,-2\,\)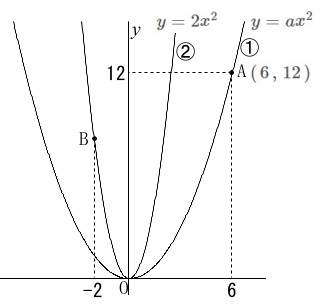 (1)
(1)
\(\,①\,\)の関数の比例定数を求めます。
関数\(\,y=ax^2\,\)が点\(\,\mathrm{A}\,(\,6\,,\,12\,)\,\)を通るので、
\(\begin{eqnarray}
12&=&a\times (6)^2\\
a&=&\underline{\underline{ \frac{1}{3} }}
\end{eqnarray}\)
(2)
直線\(\,\mathrm{AB}\,\)の式を求めます。
点\(\,\mathrm{B}\,\)は\(\,②\,\)の関数の\(\,x=2\,\)の点なので
\(\hspace{4pt}\,\mathrm{B}\,(\,-2\,,\,8\,)\)
よって2点\(\,\mathrm{A\,,\,B}\,\)
\(\,\mathrm{A}\,(\,6\,,\,12\,)\,\)
\(\,\mathrm{B}\,(\,-2\,,\,8\,)\,\)
を通る直線は
\(\hspace{10pt}\displaystyle \underline{\underline{ y=\frac{1}{2}\,x+9 }}\)
2点を通る直線の式を求めるとき、
あまり時間をかけないように練習しておくと良いですよ。
関数問題では問題になっていなくても何本も求める事が多いです。
(3)
三角形の面積を2等分する直線の傾きを求めます。
すでにまとめとして解説しているので詳しくする必要はありませんね。
ここでは頂点を通っているとは言えないので、
具体的な面積計算をします。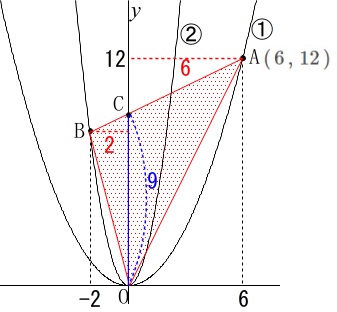 \(\,\mathrm{△OAB}\,\)の面積は底辺を\(\,\mathrm{\color{blue}{OC}}=\color{blue}{9}\,\)とすると、
\(\,\mathrm{△OAB}\,\)の面積は底辺を\(\,\mathrm{\color{blue}{OC}}=\color{blue}{9}\,\)とすると、
2つの三角形の和とみることができるので
\(\begin{eqnarray}\displaystyle
\mathrm{△OAB}&=&\mathrm{△OBC+△OAC}\\
&=&\frac{1}{2}\times 9\times 2+\frac{1}{2}\times 9\times 6\\
&=&36
\end{eqnarray}\)
\(\,\mathrm{\color{blue}{△OBC}=\color{blue}{9}}\,\)なので、
点\(\,\mathrm{C}\,\)を通る直線と\(\,\mathrm{OA}\,\)との交点を\(\,\mathrm{T}\,\)とすると
\(\,\mathrm{\color{magenta}{△OCT}=\color{magenta}{9}}\,\)となれば、
\(\,\mathrm{△ACT}\,\)と四角形\(\,\mathrm{OBCT}\,\)が等しく2等分することになります。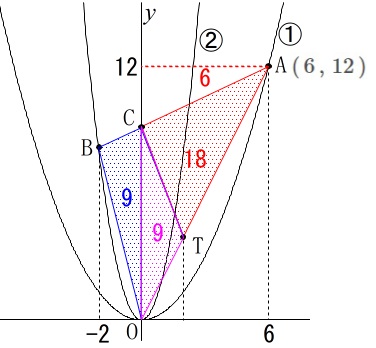 直線\(\,\mathrm{OA}\,\)は\(\,y=2x\,\)なので、
直線\(\,\mathrm{OA}\,\)は\(\,y=2x\,\)なので、
\(\hspace{4pt}\mathrm{T}\,(\,t\,,\,2t\,)\)
とすると\(\,\mathrm{△OCT}\,\)は底辺\(\,9\,\)で\(\,t\,\)が高さとなるので
\(\begin{eqnarray}
\frac{1}{2}\times 9\times t&=&9\\
t=2
\end{eqnarray}\)
このとき\(\,\mathrm{T}\,\)の座標は
\(\hspace{4pt}\mathrm{T}\,(\,2\,,\,4\,)\)
よって求める直線の傾きは、
2点\(\,\mathrm{C\,,\,T}\,\)を通るので
\(\hspace{10pt}\displaystyle \frac{4-9}{2-0}=\underline{\underline{ -\frac{5}{2} }}\)
※
答えに注意しましょう。
直線\(\,\mathrm{CT}\,\)は\(\displaystyle \,y=-\frac{5}{2}\,x+9\,\)です。
切片は分かっているので傾きだけを聞いたのでしょう。
第6問合同の証明と面積比
\(\color{black}{\fbox{6}}\)
平行四辺形と平行線があります。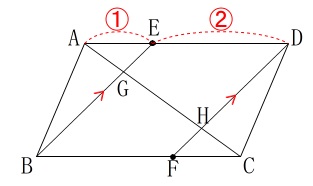 問題の条件や記号の位置は図の通りです。
問題の条件や記号の位置は図の通りです。
平行四辺形に平行線を加えると、
さらに平行四辺形ができるので分かり易い条件がたくさん出てきます。
なので簡単な解説で終わらせて頂きます。
方法は別経路でも良いので自分で試してみてください。
(1)
\(\,\mathrm{△ABG}\,\)と\(\,\mathrm{△CDH}\,\)が合同であることの証明です。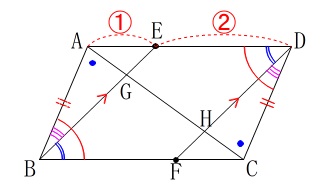 四角形\(\,\mathrm{BFDE}\,\)も平行四辺形になっていることを確認しておいてください。
四角形\(\,\mathrm{BFDE}\,\)も平行四辺形になっていることを確認しておいてください。
平行四辺形の対角は等しいので、
\(\hspace{4pt}\mathrm{\color{red}{∠ABC}=\color{red}{∠CDA}}\)
\(\hspace{4pt}\mathrm{\color{blue}{∠EBF}=\color{blue}{∠FDE}}\)
その差となるので
\(\hspace{10pt}\mathrm{\color{magenta}{∠ABG}=\color{magenta}{∠CDH}}\)
平行四辺形の対辺と平行線の錯角も合わせて合同条件がそろいますね。
「1辺とその両端の角がそれぞれ等しい。」
図で確認しておいて下さい。
⇒ 中学の図形証明問題(合同・相似)の解き方と証明の書き方ポイント
証明の書き方は決まりはないので自分でなれた方法で良いです。
(2)
三角形と平行四辺形の面積比較です。
線分\(\,\mathrm{FD}\,\)と線分\(\,\mathrm{CE}\,\)の交点を\(\,\mathrm{I}\,\)としたとき、
平行四辺形\(\,\mathrm{ABCD}\,\)の面積は\(\,\mathrm{△IHC}\,\)の何倍か?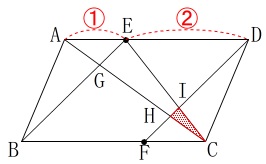 相似を利用して、
相似を利用して、
線分\(\,\mathrm{FD}\,\)がどのように分割されているかをみていきます。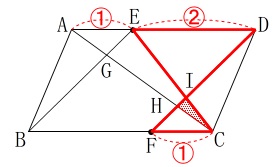 \(\,\mathrm{△EDI}\,\) ∽ \(\,\mathrm{△CFI}\,\)から
\(\,\mathrm{△EDI}\,\) ∽ \(\,\mathrm{△CFI}\,\)から
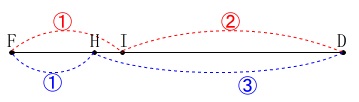
\(\hspace{10pt}\mathrm{DI:FI}=\color{red}{2}:\color{red}{1}\)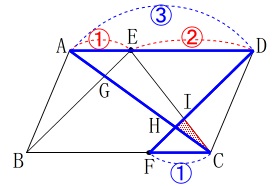 \(\,\mathrm{△ADH}\,\) ∽ \(\,\mathrm{△CFH}\,\)から
\(\,\mathrm{△ADH}\,\) ∽ \(\,\mathrm{△CFH}\,\)から
\(\hspace{10pt}\mathrm{DH:FH}=\color{blue}{3}:\color{blue}{1}\)
 分数で勧化手も良いですが、
分数で勧化手も良いですが、
線分\(\,\mathrm{FD}\,\)の全体を\(\,\color{magenta}{⑫}\,\)とすると、
(2つの線分比の和の最小公倍数です。)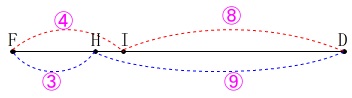 線分比が
線分比が
\(\hspace{4pt}\mathrm{FH:HI:ID}=\color{magenta}{3}:\color{magenta}{1}:\color{magenta}{8}\)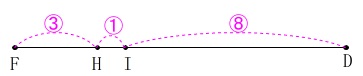 このことから\(\,\mathrm{△IHC}\,\)の面積を\(\,\color{magenta}{①}\,\)とすると
このことから\(\,\mathrm{△IHC}\,\)の面積を\(\,\color{magenta}{①}\,\)とすると
\(\begin{eqnarray}
\mathrm{△CFD}&=&\frac{3+1+8}{1}\times \mathrm{△IHC}\\
&=&12\times \mathrm{△IHC}
\end{eqnarray}\)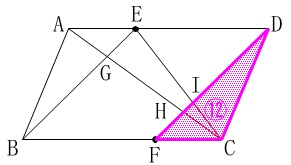 よって、平行四辺形\(\,\mathrm{ABCD}\,\)の面積\(\,S\,\)は
よって、平行四辺形\(\,\mathrm{ABCD}\,\)の面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&\color{red}{3\times 2}\times 12\times \mathrm{△IHC}\\
&=&72\times \mathrm{△IHC}
\end{eqnarray}\)
答え \(\,\underline{ 72 }倍\,\)
最後の\(\,\color{red}{3\times 2}\,\)は三角形の底辺の延長と四角形への変換ですが、
平行線で平行四辺形にして(2倍)、
さらにそれを3倍に拡大、と考えても良いですよ。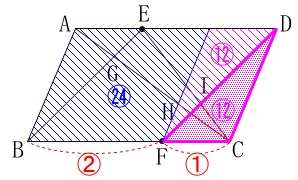 他の方法でも構いません。
他の方法でも構いません。
ポイントは線分\(\,\mathrm{FD}\,\)の部分的な比が出せるかです。
分数でも良いですが、「最小公倍数」、使えますよ。
以上です。
過去問を数年分解説してあります。
対策は基本を確実に定着させること、
と当たり前のことしか言えませんが、
傾向を知るには十分だと思いますので参考にしてください。
