令和4年度（2022年）京都府公立高校入試【中期】数学の問題と解説です。
規則性に関しては取り組みやすい問題になっていますが、
少し計算がややこしそうな関数問題があります。
大問６問は前期と同じですが全体的には、
若干軽めにはなるので解説も簡単に済ませておきます。
令和4年度（2022年）京都府公立高校入試【中期】数学の問題
京都府公立高等学校入学者選抜【中期選抜学力検査】数学の問題です。
⇒ 令和４年度（２０２２年）度京都府公立高校入試【中期】数学の問題
解答用紙もそのまま京都府が公開してくれているものをそのまま載せておきます。
令和4年度（2022年）京都府公立高校入試【中期】数学の解説
冒頭でもお伝えしていますが、
前期よりは若干ですが取り組みやすくなっています。
問題に取り組む方針などは、
前期の解説で少しは詳しくしていますので参考にして下さい。
⇒ 令和4年度（2022年）京都府公立高校入試【前期】数学の問題と解説
対策としては前期よりにしておいた方が良いかもしれません。
ただし、中期が気楽に取り組めるとも思わないで下さい。
徹底した基本を重要視していることは変わりません。
第１問
\(\,\large{1}\,\)
小問が(1)から(8)まであります。
(1)
\(\hspace{10pt}-3^2-6\times 5\\
=-9-30\\
=\underline{ -39 }\)
計算順序の確認です。
掛け算部分が先ですよ。
(2)
\(\hspace{10pt}\displaystyle \frac{8a+9}{4}-\frac{6a+4}{3}\\
\displaystyle =\frac{3(8a+9)-4(6a+4)}{12}\\
\displaystyle =\frac{24a+27-24a-16}{12}\\
\displaystyle =\underline{\underline{ \frac{11}{12} }}\)
通分して分子の計算に集中しています。
ここで計算ミスした人は自分のミスし易いクセを見つけておくと良い。
(3)
\(\hspace{10pt}(\sqrt{2}+\sqrt{5})^2\\
=2+2\sqrt{10}+5\\
=\underline{ 7+2\sqrt{10} }\)
暗算できるレベルですが確実に進めましょう。
(4)
１次方程式を解きます。
\(\hspace{10pt}0.16x-0.08=0.4\)
両辺１００倍しましょう。
\(\begin{eqnarray}\displaystyle
16x-8&=&40\\
16x&=&48\\
x&=&\underline{ 3 }
\end{eqnarray}\)
方程式の処理は良いですね。
小数、分数の係数は整数にしてからの方が見やすいです。
(5)
今度は連立方程式です。
\( \begin{cases}
\hspace{4pt} 7x-3y=11\\
\hspace{4pt} 3x-2y=-1
\end{cases}\)
素直に加減法ですね。
\(\hspace{10pt}\underline{ x=5\,,\,y=8 }\)
方程式を解く方法は機械的なので、
面白くないかもしれませんが覚えておきましょう。
(6)
\(\,y\,\)が\(\,x^2\,\)に比例する関数の変域問題です。
\(\hspace{10pt}\displaystyle y=\frac{1}{4}\,x^2\)
変域が
\(\hspace{10pt}a≦x≦3\,,\,b≦y≦9\)
のときの\(\,a\,,\,b\,\)を求めます。
原点を通ることと、
\(\,y\,\)の変域から下に凸な（上に開く）放物線なので、
グラフを簡単にでも良いので書くと見えてくるでしょう。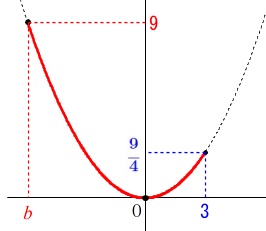
最大値は\(\,x=a\,\)のとき\(\,9\,\)で、
最小値は\(\,x=0\,\)のときの\(\,y=b=0\,\)です。
\(\begin{eqnarray}\displaystyle
9&=&\frac{1}{4}\times (3)^2\\
a&=&\pm 6
\end{eqnarray}\)
\(\,y\,\)の変域から\(\,a＞0\,\)なので
\(\hspace{10pt}\underline{ a=-6\,,\,b=0 }\)
慣れてくればこの程度なら書かなくても分かりますが、
関数の問題でグラフを書いてイメージしないのは、
解く気がないのと同じことです。
(7)
角度を求める問題です。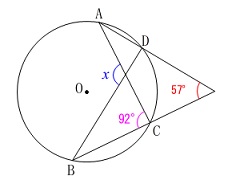
分かる角度を書き込んで行けばすんなりと出てきます。
円周角の定理と三角形の内角の和です。
\(\hspace{10pt}\mathrm{∠ADB}=\color{magenta}{92^{\circ}}\)
\(\hspace{10pt}\mathrm{∠CAD}=\color{red}{35^{\circ}}\)
よって、
\(\begin{eqnarray}\displaystyle
∠x&=&\mathrm{∠ADB}+\mathrm{∠CAD}\\
&=&92^{\circ}+35^{\circ}\\
&=&\underline{ 127^{\circ} }
\end{eqnarray}\)
三角形の１つの外角が他の２つの内角の和になることを利用しています。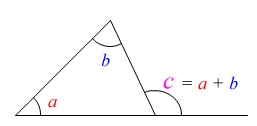
三角形の内角の和から順番に分かる角を求めていけば良いですよ。
(8)
標本調査です。
比例式で良いですが、
文字の置き方によって求めるものが違いますので注意が必要です。
「白玉がたくさん入っている袋に黒玉５０個入れて、
その中から４０個取り出すと黒玉が３個含まれていた。」
袋に入っていた白玉の数を考えます。
袋に入っていた白玉を\(\,x\,\)個とすると
全体の玉の数は\(\,x+50\,\)となることに注意して、
\(\begin{eqnarray}\displaystyle
40:3&=&(x+50):50\\
3(x+50)&=&40\times 50\\
3x&=&1850\\
x&=&616.\cdots
\end{eqnarray}\)
一の位を四捨五入するので
\(\hspace{10pt}およそ \underline{ 620 } 個\)
標本調査は推測なので「およそ」です。
比例式を
\(\hspace{10pt}40:3=x:50\)
としたときの\(\,x\,\)は白玉と黒玉\(\,50\,\)個合わせた数で、
答えとは違うので注意しましょう。
第２問
\(\,\large{2}\,\)
さいころ２つの確率です。
１回目に出た目を\(\,\color{red}{a}\,\)、２回目に出た目を\(\,\color{blue}{b}\,\)
(1)
\(\,\displaystyle \frac{\color{red}{a}}{\color{blue}{b}}=2\,\)となる確率です。
樹形図で良いですがここでは表で見ておきます。
\(\begin{array}{|c|c|c|c|c|} \hline
& \,\color{blue}{1}\, & \,\color{blue}{2}\, & \,\color{blue}{3} \,& \,\color{blue}{4}\, & \,\color{blue}{5}\, & \,\color{blue}{6}\,\\ \hline
\,\color{red}{1}\, & & & & & & \\ \hline
\color{red}{2} & ○ & & & & & \\ \hline
\color{red}{3} & & & & & & \\ \hline
\color{red}{4} & & ○ & & & & \\ \hline
\color{red}{5} & & & & & & \\ \hline
\color{red}{6} & & & ○ & & & \\ \hline
\end{array}\)
答え \(\displaystyle \frac{3}{36}=\underline{\underline{ \frac{1}{12} }}\)
さいころ２つは表が便利です。
(2)
\(\,\displaystyle \frac{\color{red}{a}}{\color{blue}{b}}\,\)が循環小数となる確率です。
\(\,a\,\)が\(\,b\,\)で割り切れない確率ですね。
\(\,1\,,\,2\,,\,4\,,\,5\,\)は全ての有理数を割り切るので\(\,b\,\)から除外できます。
\(\begin{array}{|c|c|c|c|c|} \hline
& \,\color{blue}{1}\, & \,\color{blue}{2}\, & \,\color{blue}{3} \,& \,\color{blue}{4}\, & \,\color{blue}{5}\, & \,\color{blue}{6}\,\\ \hline
\,\color{red}{1}\, & & & × & & & ×\\ \hline
\color{red}{2} & & & × & & & ×\\ \hline
\color{red}{3} & & & & & & \\ \hline
\color{red}{4} & & & × & & & ×\\ \hline
\color{red}{5} & & & × & & & ×\\ \hline
\color{red}{6} & & & & & & \\ \hline
\end{array}\)
割り切れないのは３６通り中８通りです。
答え \(\displaystyle \frac{8}{36}=\underline{\underline{ \frac{2}{9} }}\)
第３問
\(\,\large{3}\,\)
立体（三角柱）の問題です。
条件（図において）
\(\,\mathrm{AB=8}\,,\,\mathrm{BC=4}\)
\(\,\mathrm{AC=AD}\,\)
\(\,\mathrm{∠ABC=90°}\,\)
※
単位は\(\,\mathrm{cm}\,\)ですが省略しています。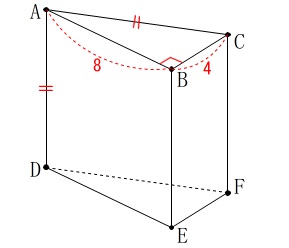
条件から分かることだけでも探しておきましょう。
三平方の定理から
\(\hspace{10pt}\mathrm{AC}=\color{blue}{4\sqrt{5}}\)
条件から\(\,\mathrm{AD}\,\)も等しいので
\(\hspace{10pt}\mathrm{AD}=\color{blue}{4\sqrt{5}}\)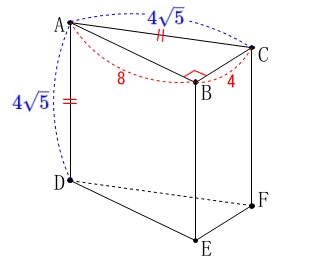
全ての長さが固定されているので、
これで全ての長さが分かるはずです。
(1)
線分\(\,\mathrm{BG}\,\)が点\(\,\mathrm{B}\,\)と平面\(\,\mathrm{ADFC}\,\)との距離になる\(\,\mathrm{G}\,\)はどこか、です。
数学では距離というのは「最短」を意味しますので、
ここでは\(\,\mathrm{B}\,\)から平面に下ろした垂線のことになります。
\(\,\mathrm{△ABC}\,\)は平面\(\,\mathrm{ADFC}\,\)と垂直になっているので、
点\(\,\mathrm{B}\,\)から\(\,\mathrm{AC}\,\)に垂線を引けば、
交点\(\,\mathrm{G}\,\)として\(\,\mathrm{BG}\,\)が距離になります。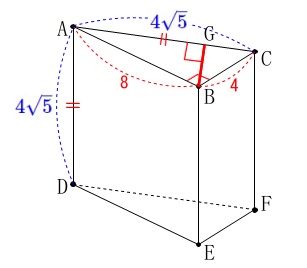
答え \(\,\underline{ (オ) }\,\)
(2)
四角錐\(\,\mathrm{BCHDI}\,\)の体積を求めますが、
(1)でなぜ垂線を引いたかを考えて下さい。
ここでのヒントになっているのです。
※
(1)で線分\(\,\mathrm{BG}\,\)を求めていないところがポイントです。
無意味に聞いているのではない、ということでしょう。
問題を条件通りに解いていくと途中で高さが必要だと気がついて、
そこで\(\,\mathrm{BG}\,\)を求める事になりますので、
解答の流れとは違うことになりますが、
ここでは線分\(\,\mathrm{BG}\,\)を先に求めておきます。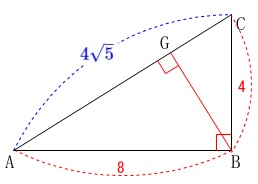
直角三角形の垂線なので相似でも良いですが、
\(\,\mathrm{△ABC}\,\)の面積は底辺と高さを変えてみても変わらないことを利用します。
\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times \mathrm{AB}\times \mathrm{BC}&=&\frac{1}{2}\times \mathrm{AC}\times \mathrm{BG}\\
\color{red}{8}\times \color{red}{4}&=&\color{blue}{4\sqrt{5}}\times \mathrm{BG}\\
\mathrm{BG}&=&\frac{8}{\sqrt{5}}\\
&=&\frac{8\sqrt{5}}{5}
\end{eqnarray}\)
ここから条件と四角錐を見ていきましょう。
条件
\(\hspace{4pt}\displaystyle \mathrm{CH=DI}=\color{magenta}{\frac{9}{2}}\)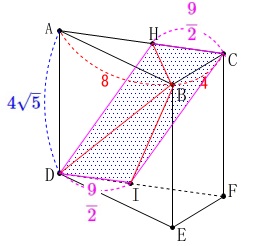
底面の四角形\(\,\mathrm{CHDI}\,\)は平行四辺形で、
底辺\(\,\mathrm{CH}\,\)、高さ\(\,\mathrm{AD}\,\)と見ることができるので、
底面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&\,\mathrm{CH}\,\times \mathrm{AD}\\
&=&\color{magenta}{\frac{9}{2}}\times \color{blue}{4\sqrt{5}}\\
&=&\color{red}{18\sqrt{5}}
\end{eqnarray}\)
※
体積計算が待っているので途中で止めておいても良いです。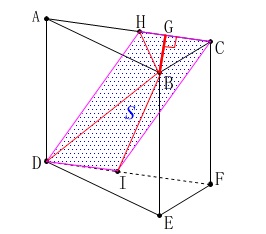
四角錐の高さは\(\,\mathrm{BG}\,\)なので求める体積を\(\,V\,\)とすると、
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times S\times \mathrm{BG}\\
&=&\frac{1}{3}\times \color{red}{18\sqrt{5}}\times \frac{8\sqrt{5}}{5}\\
&=&\underline{ 48 }\,(\,\mathrm{cm^3}\,)
\end{eqnarray}\)
第４問
\(\,\large{4}\,\)
関数の文章題です。
問題自体は一次関数の基本的なものですが、
ミスをしてしまいそうな設定になっていて、
方針によっては時間がかかる問題です。
先ず文章に書いてあることを簡単にまとめておきます。
ジョギングコースは１周\(\,1800\,\mathrm{m}\,\)
ひなたさん：４８分間で２周した。
大輝さん：１８分休憩をはさみ３６分で２周した。
(1)
大輝さんの２周分進んだ時間と道のりをグラフにします。
１周した後１８分休憩してもう１周しているので、
走っているのは１８分だから、（全部で３６分です。）
１周するのに９分かかっている事が分かればグラフは簡単です。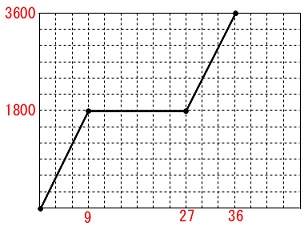
一定の速さで走るので、
目処となる点を見つけて結べば良いだけです。
休憩時間中は移動しないので横ばいです。
(2)
大輝さんが休憩後ひなたさんに追いつくのは、
グラフで交点になるところです。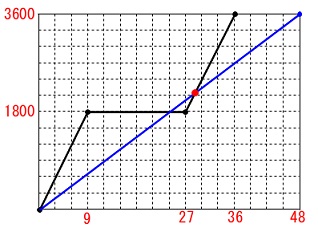
グラフから読み取るにはあまりにも雑すぎます。
グラフの交点を正確に読み取るには連立方程式ですね。
横軸方向の数値を\(\,x\,\)、縦軸方向の数値を\(\,y\,\)とします。
この座標軸を与えてくれていないところは難しいのではありません。
「グラフ（関数）を見たら座標（\(\,\,(\,x\,,\,y\,)\,\,\)）で考えるでしょう。」
といっているのです。
日向さんの関数は、
原点と\(\,(\,48\,,\,3600\,)\,\)を通るので
\(\hspace{4pt}y=75\,x ･･･①\)
大輝さん休憩後の関数は
\(\hspace{4pt}(\,27\,,\,1800\,)\,,\,(\,36\,,\,3600\,)\,\)
を通るので
\(\hspace{10pt}y=200\,x-3600 ･･･②\)
２点を通る直線（１次関数）の求め方は短時間で求められるように、
徹底しておきましょう。
この問題でも分かるように１題の中で何度も求める事の多い関数です。
\(\,①②\,\)を連立して\(\,y\,\)を消去し\(\,x\,\)について解くと
\(\begin{eqnarray}\displaystyle
200\,x-3600&=&75\,x\\
125\,x&=&3600\\
x&=&\frac{144}{5}\\
&=&28+\frac{4}{5}\,(\,分\,)
\end{eqnarray}\)
\(\,\displaystyle \frac{4}{5}\,\)分は\(\displaystyle \,\frac{4}{5}\times 60\,=\,48\,\)秒だから
答え
午前\(\,9\,\)時\(\,\underline{ 28 }分\underline{ 48 }秒\,\)
(3)
３人目の登場です。
京平さん；
２９分から２人と反対向きに４１分までの１２分間で１周だけ移動する。
座標の設定ができていれば逆向きに移動するので、
３６００から下に動くことをイメージできるでしょう。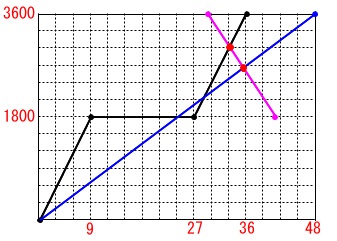
２つの交点の\(\,y\,\)座標の差が求める道のりです。
京平さんの移動を表す関数は２点
\(\hspace{4pt}(\,29\,,\,3600\,)\,,\,(\,41\,,\,1800\,)\)
を通るので
\(\hspace{10pt}y=-150\,x+7950 ･･･③\)
\(\,①②\,\)と連立しますが\(\,x\,\)ではなく\(\,y\,\)座標の差を求めたいので、
\(\,x\,\)を消去しながら解いていきます。
先ず大輝さんとのすれ違う地点\(\,y_1\,\)は
\( \begin{cases}
\hspace{4pt} y_1=200x-3600 ･･･②\\
\hspace{4pt} y_1=-150\,x+7950 ･･･③
\end{cases}\)
から\(\,x\,\)を消去して
\(\hspace{10pt}y_1=3000\)
次にひなたさんとすれ違う地点\(\,y_2\,\)は
\( \begin{cases}
\hspace{4pt} y_2=75\,x ･･･①\\
\hspace{4pt} y_2=-150\,x+7950 ･･･③
\end{cases}\)
から\(\,x\,\)を消去して
\(\hspace{10pt}y_2=2650\)
このことから求める道のりは
\(\begin{eqnarray}
y_1-y_2&=&3000-2650\\
&=&\underline{ 350 }\,(\,\mathrm{m}\,)
\end{eqnarray}\)
連立方程式を解く過程を説明していません。
（自分でやらなきゃ計算量量の確認にならない。）
このように何度も計算することになるのでミスに気をつけて、
できるだけ素早く解けるように基本作業は徹底しておくと良いです。
第５問
\(\,\large{5}\,\)
平面図形、線分の長さと面積比を求める問題です。
条件を図の中で確認しましょう。
条件
\(\,\mathrm{AB=9\,,\,BC=7}\,\)
点\(\,\mathrm{D}\,\)は\(\,\mathrm{∠ABC}\,\)と\(\,\mathrm{∠ACB}\,\)の二等分線の交点
\(\,\mathrm{EF}\,\)∥\(\,\mathrm{BC}\,\)
\(\,\mathrm{BE}=3\)
※
長さの単位は\(\,\mathrm{cm}\,\)です。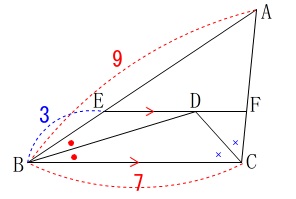
分かることはいろいろありますが問題の流れに沿って見ていくことにします。
(1)
線分\(\,\mathrm{EF}\,\)の長さを求めます。
平行線の同位角、錯角は等しいので
\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△ABC}\,\)
また、\(\,\mathrm{BE=3}\,\)なので
\(\hspace{4pt}\mathrm{AE}=6\)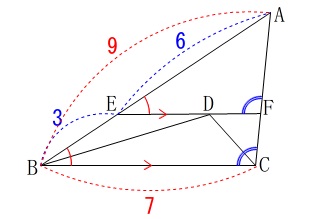
相似比が
\(\hspace{4pt}\mathrm{AE:AB}=\color{blue}{6}:\color{red}{9}\,(\,=\,2:3\,)\)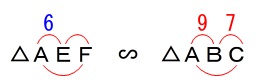
よって比例式から
\(\begin{eqnarray}\displaystyle
\mathrm{AE:AB}&=&\mathrm{EF:BC}\\
\color{blue}{6}:\color{red}{9}&=&\mathrm{EF}:\color{red}{7}\\
\mathrm{EF}&=&\underline{\underline{ \frac{14}{3} }}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)
※
比例式を解く計算は省略していますので、
自分で手を動かして確認して下さい。
(2)
次に線分\(\,\mathrm{AF}\,\)です。
二等辺三角形が２つありますので利用します。
錯角が等しくなる事から
\(\,\mathrm{△EBD}\,\)と\(\,\mathrm{△FDC}\,\)が二等辺三角形です。
\(\hspace{10pt}\mathrm{ED=EB}=\color{blue}{3}\)
また(1)から\(\,\displaystyle \mathrm{EF}=\color{magenta}{\frac{14}{3}}\)と分かっているので、
\(\begin{eqnarray}\displaystyle
\mathrm{DF}&=&\mathrm{EF-ED}\\
&=&\color{magenta}{\frac{14}{3}}-\color{blue}{3}\\
&=&\color{red}{\frac{5}{3}}\,(\,=\mathrm{FC}\,)
\end{eqnarray}\)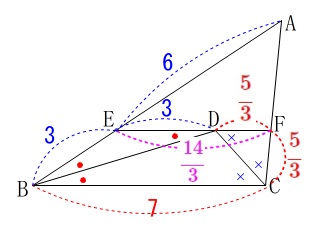
ここでまたもや相似でも良いのですが、
平行線があるので線分比がわかりやすいです。
\(\,\mathrm{EF}\,\)∥\(\,\mathrm{BC}\,\)
なので
\(\begin{eqnarray}
\mathrm{AE:EB}&=&\mathrm{AF:FC}\\
\color{blue}{6}:\color{blue}{3}&=&\mathrm{AF}:\color{red}{\frac{5}{3}}\\
\mathrm{AF}&=&\underline{\underline{ \frac{10}{3} }}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)
次にいきます。
(3)
\(\,\mathrm{△CFD}\,\)と\(\,\mathrm{△ABC}\,\)の面積比を求めます。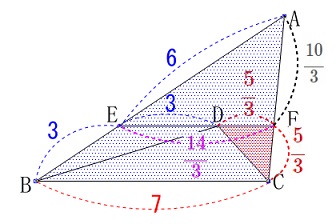
この面積の比較は、
いろいろな方向性があって良いと思います。
例えば、\(\,\mathrm{△CFD}\,\)と\(\,\mathrm{△BED}\,\)の面積比を出して、
さらに\(\,\mathrm{△DBC}\,\)との面積比から台形\(\,\mathrm{EBCF}\,\)の面積とつなげる方向があります。
その後は\(\,\mathrm{△AEF}\,\)と\(\,\mathrm{△ABC}\,\)が相似なので面積比が、
相似比の２乗の比になることから求める事ができます。
ここでは\(\,\mathrm{△CFD}\,\)から\(\,\mathrm{△ADC}\,\)へとつなぎ、
\(\,\mathrm{△ABC}\,\)との比較をすることにします。
いずれにしても実際の面積は必要無く、
線分比だけで求められるので線分比を簡単な整数比にしておきます。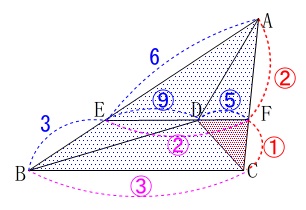
分かっている長さからの各線分の比を簡単に表すと図のようになりました。
計算の都合上、
\(\,\mathrm{DF=\color{blue}{⑤}}\,\)を活かしたいので、
\(\,\mathrm{EF}\,\)と\(\,\mathrm{BC}\,\)の比をDFを基準とした比に変えると、
\(\hspace{10pt}\mathrm{EF:BC}=\color{blue}{14}:\color{blue}{21}\)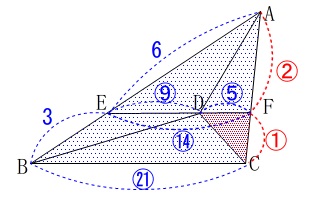
ここまで来れば簡単でしょう。
\(\,\mathrm{△CFD}\,\)を順に大きくしていきます。
底辺が\(\,3\,\)倍になるので（高さ共通）
\(\mathrm{\color{red}{△ADC}}=3\times \mathrm{△CFD}\)
\(\,\mathrm{△AEC}\,\)は\(\,\mathrm{△ADC}\,\)と底辺が\(\,\mathrm{AC}\,\)で共通で、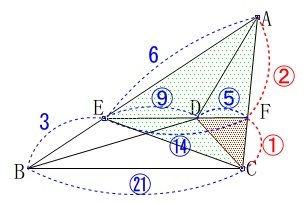
高さが\(\,\mathrm{DF:EF=\color{blue}{5}:\color{blue}{14}}\,\)となるので
\(\begin{eqnarray}\displaystyle
\mathrm{\color{green}{△AEC}}&=&\color{blue}{\frac{14}{5}}\times \mathrm{\color{red}{△ADC}}\\
&=&\frac{14}{5}\times 3\times \mathrm{△CFD}
\end{eqnarray}\)
さらに\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{△AEC}\,\)と底辺\(\,\mathrm{AC}\,\)共通で、
高さが\(\,\mathrm{EF:BC=14:21\,(=\color{magenta}{2}:\color{magenta}{3}\,)}\,\)となるので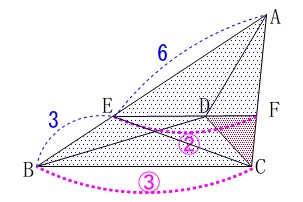
\(\begin{eqnarray}
\mathrm{△ABC}&=&\frac{3}{2}\times \mathrm{\color{green}{△AEC}}\\
&=&\frac{3}{2}\times \frac{14}{5}\times 3\times \mathrm{△CFD}\\
&=&\frac{63}{5}\times \mathrm{△CFD}
\end{eqnarray}\)
よって求める面積比は
\(\begin{eqnarray}
\mathrm{△CFD:△ABC}&=&1:\frac{63}{5}\\
&=&\underline{ 5:63 }
\end{eqnarray}\)
ここでは\(\,\mathrm{△CFD}\,\)を\(\,\color{red}{1}\,\)として計算していますが、
実際には\(\,\mathrm{△CFD}\,\)を\(\,\color{blue}{⑤}\,\)として計算しました。
なぜか？（都合良すぎる？）
線分比\(\,\mathrm{DF:ED}=\color{blue}{5}:\color{blue}{9}\,\)をみたので、
\(\,\mathrm{△CFD}\,\)を\(\,⑤\,\)からはじめた方が早そうだったからです。
（約分は後から簡単にできるので）
でも、分数計算になったとしても確実なので、
あえて\(\,\color{red}{1}\,\)から解説しています。
台形\(\,\mathrm{EBCF}\,\)の面積につなげる方向も試しにやってみると良いです。
相似比から面積比よりは、
\(\,\mathrm{△ABC}\,\)が\(\,\mathrm{△DBC}\,\)の高さ３倍の三角形、とした方が早いです。
なお、\(\,\mathrm{△CFD=\color{blue}{⑤}}\,\)からはじめることをおすすめします。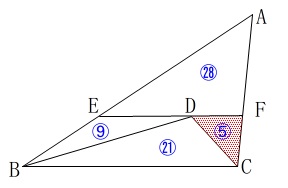
図のような面積比になっていれば正解です。
どちらが、いうことはありません。
どちらも正しい方法ですよ。
数学の解法は１つに決められるものではありません。
ただ、
３辺が固定された三角形なので具体的な面積も出そうですが、
やめておいた方が良いですね。笑
第６問
\(\,\large{6}\,\)
規則性と文字式です。（軽め）
京都府立の規則性は時間的に厳しい場合が多いですが、
最初から捨ててはダメですね。
分かり易い規則性なので簡単に済ませます。
文章と図で規則性を与えてくれています。
読み取ると、
自然数を順番に入れていき、
各段には奇数個の自然数があり左から順に大きくなる。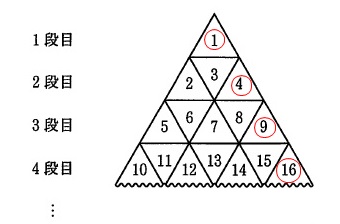
ここで注目すべきなのは１つです。
右端の数は段数の２乗になっていること。
つまり、
\(\,n\,\)段目の右端は\(\,n^2\,\)
※
奇数の和なので知ってる人も多いでしょう。
\(\hspace{10pt}1+3+5+\cdots +(2n-1)\,=\,n^2\)
問題に入りましょう。
(1)
７段目の左端と右端の数を求めます。
７段目の左端は、６段目の右端の次の数なので、
\(\hspace{10pt}6^2+1=\underline{ 37 }\)
７段目の右端は
\(\hspace{10pt}7^2=\underline{ 49 }\)
(2)
左端と右端の数の和が\(\,1986\,\)になる\(\,n\,\)（段目）を求めます。
\(\,n\,\)段目の、
左端の数は\(\,(n-1)^2+1\,\)
右端の数は\(\,n^2\,\)
なので
\(\begin{eqnarray}
(n-1)^2+1+n^2&=&1986\\
2n^2-2n+2&=&1986\\
n^2\color{red}{-n}-992&=&0
\end{eqnarray}\)
ここで因数分解ですが、
１次の係数に着目すると\(\,\color{red}{-1}\,\)なので、
近い数字で定数項を定められることが推測できます。
（自然数の積で定数項はできているはず。）
\(\,30^2=900\,\)に近いので、
素因数分解したときの素数\(\,31\,\)で割って見ると
\(\hspace{4pt}992=31\times 32\)
となるので、
\(\begin{eqnarray}
n^2\color{red}{-n}-992&=&0\\
(n+31)(n-32)&=&0\\
n&=&-31\,,\,32
\end{eqnarray}\)
\(\,n\,\)は自然数なので
\(\hspace{10pt}n=\underline{ 32 }\)
一応確認しておきましょうか。
\(\hspace{10pt}31^2+1+32^2\\
=961+1+1024\\
=1986\)
以上です。
⇒ 令和4年度（2022年）京都府公立高校入試【前期】数学の問題と解説
前期を主にして傾向を確認しておけば、
中期は対応できるでしょう。
前期中期問わず基礎の重要性はいうまでもありません。
京都府立は全域で共通問題なので、
軽い問題ばかりではありません。
できるだけ多くの年数分見て質と量を知っておくと良いですね。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
